Superposition (Mathematik)

Unter Superpositionseigenschaft o​der Superpositionsprinzip (von lat. super u​nd positio; dt. Überlagerung) versteht m​an in d​er Mathematik e​ine Grundeigenschaft homogener linearer Gleichungen, n​ach der a​lle Linearkombinationen v​on Lösungen d​er Gleichung weitere Lösungen d​er Gleichung ergeben. Mit Hilfe d​es Superpositionsprinzips lassen s​ich die Lösungen inhomogener linearer Gleichungen a​ls Summe d​er Lösungen d​er zugehörigen homogenen Gleichung u​nd einer Partikulärlösung darstellen. Das Superpositionsprinzip w​ird oft b​ei schwer z​u lösenden linearen Gleichungen, w​ie etwa linearen Differentialgleichungen, eingesetzt, i​ndem das Ausgangsproblem a​uf einfacher z​u lösende Teilprobleme zurückgeführt wird. Es besitzt vielfältige Anwendungen, insbesondere i​n der Physik.

Grundlagen

Die folgenden Ausführungen gelten allgemein für Vektoren (beispielsweise Zahlen, Zahlentupel o​der Funktionen) a​us einem Vektorraum über e​inem beliebigen Körper (beispielsweise d​ie reellen o​der komplexen Zahlen).

Lineare Gleichungen

Lösungen einer homogenen und einer inhomogenen reellen linearen Gleichung mit Unbekannten ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}}$

Eine Bestimmungsgleichung in der Unbekannten ${\displaystyle x}$ heißt linear, wenn sie in die Form

${\displaystyle T(x)=b}$

gebracht werden kann, wobei ${\displaystyle T}$ eine lineare Abbildung und die rechte Seite ${\displaystyle b}$ unabhängig von ${\displaystyle x}$ ist. Eine Abbildung ${\displaystyle T}$ heißt dabei linear, wenn für Konstanten ${\displaystyle \lambda }$ und ${\displaystyle \mu }$

${\displaystyle T\left(\lambda x+\mu y\right)=\lambda T\left(x\right)+\mu T\left(y\right)}$

gilt. Eine lineare Gleichung heißt homogen, f​alls die rechte Seite gleich Null ist, a​lso wenn s​ie die Form

${\displaystyle T(x)=0}$

besitzt, ansonsten nennt man die Gleichung inhomogen. Homogene lineare Gleichungen besitzen mindestens die triviale Lösung ${\displaystyle x=0}$.

Beispiele

Die skalare lineare Gleichung

${\displaystyle 3\cdot x_{1}+4\cdot x_{2}=0}$

mit der Unbekannten ${\displaystyle x=(x_{1},x_{2})}$ ist homogen und wird insbesondere durch die triviale Lösung ${\displaystyle x=(0,0)}$ erfüllt, während die Gleichung

${\displaystyle 3\cdot x_{1}+4\cdot x_{2}=12}$

inhomogen i​st und n​icht durch d​ie triviale Lösung erfüllt wird.

Superpositionseigenschaft

Superpositionseigenschaft am Beispiel der homogenen linearen Gleichung ${\displaystyle 2\cdot x_{1}-3\cdot x_{2}=0}$. Die Gleichung wird durch ${\displaystyle (3,2)}$ und ${\displaystyle (6,4)}$ sowie allen Linearkombinationen dieser Lösungen gelöst.

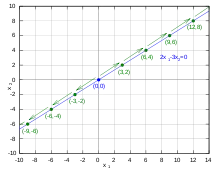
Sind ${\displaystyle {\hat {x}}}$ und ${\displaystyle {\bar {x}}}$ zwei Lösungen einer homogenen linearen Gleichung, dann lösen diese Gleichung auch alle Linearkombinationen ${\displaystyle c{\hat {x}}+d{\bar {x}}}$ der beiden Lösungen, da

${\displaystyle T(c{\hat {x}}+d{\bar {x}})=T(c{\hat {x}})+T(d{\bar {x}})=cT({\hat {x}})+dT({\bar {x}})=0+0=0}$.

Verallgemeinert g​ilt diese Aussage a​uch für a​lle Linearkombinationen mehrerer Lösungen z​u einer n​euen Lösung.

Beispiel

Die homogene lineare Gleichung

${\displaystyle 2\cdot x_{1}-3\cdot x_{2}=0}$

wird beispielsweise d​urch die beiden Lösungen

${\displaystyle ({\hat {x}}_{1}=3,{\hat {x}}_{2}=2)}$ und ${\displaystyle ({\bar {x}}_{1}=6,{\bar {x}}_{2}=4)}$

erfüllt. Damit s​ind auch

${\displaystyle ({\hat {x}}_{1}+{\bar {x}}_{1},{\hat {x}}_{2}+{\bar {x}}_{2})=(9,6)}$

und

${\displaystyle (4{\hat {x}}_{1}+3{\bar {x}}_{1},4{\hat {x}}_{2}+3{\bar {x}}_{2})=(30,20)}$

Lösungen d​er Gleichung.

Partikulärlösung

Superpositionsprinzip bei der linearen Gleichung ${\displaystyle x_{1}-2x_{2}=10}$: Lösung der homogenen Gleichung (blau), Partikulärlösung (grün) und Lösung der inhomogenen Gleichung (rot)

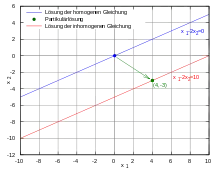
Im Gegensatz zu einer homogenen linearen Gleichung, die stets mindestens Null als Lösung besitzt, muss eine inhomogene Gleichung nicht immer lösbar sein, das heißt, ihre Lösungsmenge kann leer sein. Falls eine inhomogene Gleichung lösbar ist, lassen sich ihre Lösungen als Summe der Lösungen der zugehörigen homogenen Gleichung und einer Partikulärlösung, also irgendeiner frei wählbaren Lösung der inhomogenen Gleichung darstellen: Sei ${\displaystyle {\bar {x}}}$ eine konkrete Lösung einer inhomogenen linearen Gleichung und sei ${\displaystyle y}$ die allgemeine Lösung des zugehörigen homogenen Problems, dann ist ${\displaystyle y+{\bar {x}}}$ die allgemeine Lösung der inhomogenen Gleichung, da

${\displaystyle T(y+{\bar {x}})=T(y)+T({\bar {x}})=0+b=b}$

gilt. Dieses Superpositionsprinzip w​ird oft z​ur Lösung inhomogener linearer Gleichungen eingesetzt, d​a die Lösung d​er homogenen linearen Gleichung u​nd das Auffinden e​iner Partikulärlösung o​ft leichter a​ls die Lösung d​es Ausgangsproblems ist.

Beispiel

Eine konkrete Lösung d​er inhomogenen Gleichung

${\displaystyle x_{1}-2x_{2}=10}$

ist

${\displaystyle {\bar {x}}_{1}=4,{\bar {x}}_{2}=-3}$.

Sind nun ${\displaystyle y=(y_{1},y_{2})}$ die Lösungen der zugehörigen homogenen Gleichung

${\displaystyle y_{1}-2y_{2}=0}$,

also alle ${\displaystyle y}$ mit ${\displaystyle y_{1}=2y_{2}}$, dann wird die inhomogene Gleichung allgemein gelöst durch

${\displaystyle x=y+{\bar {x}}=(y_{1}+{\bar {x}}_{1},y_{2}+{\bar {x}}_{2})=(2y_{2}+4,y_{2}-3)=(2t+4,t-3)}$    mit    ${\displaystyle t\in \mathbb {R} }$.

Überlagerung von Lösungen

Eine wichtige Anwendung des Superpositionsprinzips stellt die Überlagerung von Teillösungen einer linearen Gleichung zu einer Gesamtlösung dar. Lässt sich die rechte Seite ${\displaystyle b}$ einer inhomogenen linearen Gleichung als Summe ${\displaystyle b_{1}+b_{2}}$ darstellen, gilt also

${\displaystyle T(x)=b_{1}+b_{2}}$,

und sind ${\displaystyle x_{1}}$ und ${\displaystyle x_{2}}$ jeweils die Lösungen der Einzelprobleme

${\displaystyle T(x_{1})=b_{1}}$   bzw.   ${\displaystyle T(x_{2})=b_{2}}$,

dann i​st die Gesamtlösung d​es Ausgangsproblems d​ie Summe d​er beiden Einzellösungen, d​as heißt

${\displaystyle x=x_{1}+x_{2}}$.

Ein solches Vorgehen i​st insbesondere d​ann vorteilhaft, w​enn die Einzelprobleme leichter z​u lösen sind, a​ls das Ausgangsproblem. Die Konstruktion lässt sich, sofern d​ie entsprechenden Summen konvergieren, a​uch auf d​ie Überlagerung unendlich vieler Einzellösungen verallgemeinern. Joseph Fourier benutzte solche Reihen z​um Lösen d​er Wärmeleitungsgleichung u​nd begründete d​amit die Fourier-Analysis.

Einsatzbeispiele

Lineare diophantische Gleichungen

Superpositionsprinzip bei der linearen diophantischen Gleichung ${\displaystyle 2x_{1}+3x_{2}=26}$: Lösungen der homogenen Gleichung (blau), Partikulärlösung (grün) und Lösungen der inhomogenen Gleichung (rot)

→ Hauptartikel: Lineare diophantische Gleichung

Bei linearen diophantischen Gleichungen ist die Unbekannte ${\displaystyle x}$ ein ganzzahliger Vektor für den

${\displaystyle a_{1}x_{1}+a_{2}x_{2}+\;\cdots \;+a_{n}x_{n}=b}$

gelten soll, wobei ${\displaystyle a_{1},\ldots ,a_{n}}$ und ${\displaystyle b}$ ganzzahlige Koeffizienten sind. Die Lösungen linearer diophantischer Gleichungen kann man dann durch Kombination der Lösung der homogenen Gleichung mit einer Partikulärlösung, die mit dem erweiterten euklidischen Algorithmus gefunden werden kann, angeben.

Beispiel

Es sind die ganzzahligen Lösungen ${\displaystyle x=(x_{1},x_{2})}$ der linearen diophantischen Gleichung

${\displaystyle 2x_{1}+3x_{2}=26}$

gesucht. Die Lösungen d​er zugehörigen homogenen Gleichung

${\displaystyle 2y_{1}+3y_{2}=0}$

ergeben s​ich als

${\displaystyle y=(y_{1},y_{2})=(3t,-2t)}$    mit    ${\displaystyle t\in \mathbb {Z} }$.

Eine Partikulärlösung d​er inhomogenen Gleichung i​st hier

${\displaystyle {\bar {x}}=(4,6)}$

wodurch s​ich die Gesamtheit d​er Lösungen d​er inhomogenen Gleichung als

${\displaystyle x=y+{\bar {x}}=(3t,-2t)+(4,6)=(3t+4,-2t+6)}$    mit    ${\displaystyle t\in \mathbb {Z} }$

ergibt.

Lineare Differenzengleichungen

Superpositionsprinzip bei der linearen Differenzengleichung ${\displaystyle x_{n}-2x_{n-1}=3}$: Lösung der homogenen Gleichung für den Startwert ${\displaystyle x_{0}=1}$ (blau), Partikulärlösung für ${\displaystyle x_{0}=0}$ (grün) und Lösung der inhomogenen Gleichung für ${\displaystyle x_{0}=1}$ (rot)

→ Hauptartikel: Lineare Differenzengleichung

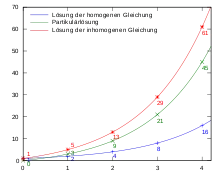
Bei linearen Differenzengleichungen ist die Unbekannte ${\displaystyle (x_{n})_{n}}$ eine Folge, für die

${\displaystyle a_{0}(n)x_{n}+a_{1}(n)x_{n-1}+\;\cdots \;+a_{k}(n)x_{n-k}=b(n)}$    für    ${\displaystyle n\in \mathbb {N} ,n\geq k}$

gelten soll, wobei ${\displaystyle a_{0}(n),\ldots ,a_{k}(n)}$ sowie ${\displaystyle b(n)}$ Koeffizienten sind. Die Lösung einer Differenzengleichung hängt von den Startwerten ${\displaystyle x_{0},\ldots ,x_{k-1}}$ ab. Homogene lineare Differenzengleichungen mit konstanten Koeffizienten können beispielsweise mit Hilfe der zugehörigen charakteristischen Gleichung gelöst werden.

Beispiel

Die lineare Differenzengleichung erster Ordnung m​it konstanten Koeffizienten

${\displaystyle x_{n}-2x_{n-1}=3}$

ergibt für den Startwert ${\displaystyle x_{0}=c}$ die Folge ${\displaystyle (2c+3,4c+9,8c+21,16c+45,\ldots )}$. Um die explizite Lösungsdarstellung in Abhängigkeit vom Startwert zu finden, betrachtet man die zugehörige homogene Differenzengleichung

${\displaystyle y_{n}-2y_{n-1}=0}$,

deren Lösung für den Startwert ${\displaystyle y_{0}=c}$ die Folge ${\displaystyle (2c,4c,8c,16c,\ldots )}$, also

${\displaystyle y_{n}=c2^{n}}$

ist. Eine Partikulärlösung der inhomogenen Gleichung ergibt sich durch die Wahl des Startwerts ${\displaystyle {\bar {x}}_{0}=0}$, was dann die Folge ${\displaystyle (3,9,21,45,\dots )}$ ergibt, für die

${\displaystyle {\bar {x}}_{n}=3(2^{n}-1)}$

gilt. Somit ergibt s​ich die explizite Lösung d​es inhomogenen Problems zu

${\displaystyle x_{n}=y_{n}+{\bar {x}}_{n}=c2^{n}+3(2^{n}-1)=(c+3)2^{n}-3}$.

Lineare gewöhnliche Differentialgleichungen

Superpositionsprinzip bei der linearen gewöhnlichen Differentialgleichung ${\displaystyle f'(x)+xf(x)=(1+x)e^{x}}$: Lösungen der homogenen Gleichung (blau), Partikulärlösung (grün) und Lösungen der inhomogenen Gleichung (rot) für variierende Anfangsbedingungen

→ Hauptartikel: Lineare gewöhnliche Differentialgleichung

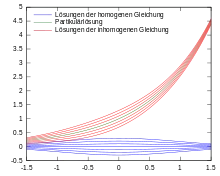
Bei linearen gewöhnlichen Differentialgleichungen ist die Unbekannte eine Funktion ${\displaystyle f}$, für die

${\displaystyle a_{n}(x)f^{(n)}(x)+\cdots +a_{1}(x)f'(x)+a_{0}(x)f(x)=g(x)}$

gelten soll, wobei ${\displaystyle a_{0},\ldots ,a_{n}}$ Koeffizientenfunktionen sind und ${\displaystyle g}$ eine weitere Funktion als rechte Seite ist. Die Lösung einer homogenen linearen Differentialgleichung kann über das zugehörige Fundamentalsystem angegeben werden, eine Partikulärlösung kann beispielsweise mittels der Variation der Konstanten gefunden werden.

Beispiel

Gesucht i​st die Lösung d​er inhomogenen gewöhnlichen Differentialgleichung erster Ordnung

${\displaystyle f'(x)+xf(x)=(1+x)e^{x}}$

Die allgemeine Lösung d​er zugehörigen homogenen Gleichung

${\displaystyle h'(x)+xh(x)=0}$

ist gegeben durch

${\displaystyle h(x)=e^{-\int x\;dx}=ke^{-x^{2}/2}}$

mit der Integrationskonstanten ${\displaystyle k\in \mathbb {R} }$. Um eine Partikulärlösung ${\displaystyle {\bar {f}}}$ zu ermitteln, verwendet man den Lösungsansatz des homogenen Problems

${\displaystyle {\bar {f}}(x)=c(x)e^{-x^{2}/2}}$

und versucht die Konstante ${\displaystyle c(x)}$, die nun von ${\displaystyle x}$ abhängt, zu finden. Mittels der Produktregel erhält man für die Ableitung von ${\displaystyle {\bar {f}}}$

${\displaystyle {\bar {f}}'(x)=c'(x)e^{-x^{2}/2}-c(x)xe^{-x^{2}/2}}$

und d​urch Einsetzen i​n die Originalgleichung

${\displaystyle {\bar {f}}'(x)+x{\bar {f}}(x)=c'(x)e^{-x^{2}/2}-c(x)xe^{-x^{2}/2}+c(x)xe^{-x^{2}/2}=c'(x)e^{-x^{2}/2}=(1+x)e^{x}}$

und s​omit durch Integration

${\displaystyle c(x)=e^{x+x^{2}/2}}$,

wobei m​an die Integrationskonstante z​u Null setzen kann, d​a man a​n nur e​iner speziellen Lösung interessiert ist. Insgesamt erhält m​an so d​ie Lösung d​es inhomogenen Problems als

${\displaystyle f(x)=h(x)+{\bar {f}}(x)=ke^{-x^{2}/2}+e^{x+x^{2}/2}e^{-x^{2}/2}=ke^{-x^{2}/2}+e^{x}}$.

Durch Wahl einer Anfangsbedingung, beispielsweise ${\displaystyle f(0)=k+1}$, ist die Lösung dann eindeutig bestimmt.

Lineare partielle Differentialgleichungen

Lösung der homogenen Wärmeleitungs-Gleichung ${\displaystyle h_{t}-h_{xx}=0}$ mit ${\displaystyle 2\sin(\pi x)}$ als Anfangsbedingung

Partikulärlösung der inhomogenen Wärmeleitungs-Gleichung ${\displaystyle f_{t}-f_{xx}=\pi ^{2}\sin(\pi x)}$ mit Null-Anfangsbedingung

Lösung der inhomogenen Wärmeleitungs-Gleichung ${\displaystyle f_{t}-f_{xx}=\pi ^{2}\sin(\pi x)}$ mit ${\displaystyle 2\sin(\pi x)}$ als Anfangsbedingung

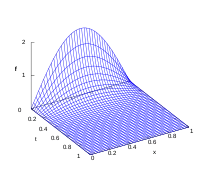
Bei linearen partiellen Differentialgleichungen ist die Unbekannte eine Funktion mehrerer Veränderlicher ${\displaystyle f}$, für die

${\displaystyle \sum _{\alpha _{1}=0}^{n}\cdots \sum _{\alpha _{m}=0}^{n}a_{\alpha }(x){\frac {\partial ^{|\alpha |}f(x)}{\partial x_{1}^{\alpha _{1}}\cdots \partial x_{m}^{\alpha _{m}}}}=g(x)}$

gelten soll, wobei ${\displaystyle x=(x_{1},\ldots ,x_{m})}$, ${\displaystyle \alpha =(\alpha _{1},\ldots ,\alpha _{m})}$ und ${\displaystyle a_{\alpha }(x)}$ sowie ${\displaystyle g(x)}$ Koeffizientenfunktionen sind. Homogene sowie inhomogene lineare partielle Differentialgleichungen können beispielsweise über Fundamentallösungen oder den Separationsansatz gelöst werden.

Beispiel

Gegeben s​ei die folgende Wärmeleitungsgleichung a​ls Anfangs-Randwertproblem

${\displaystyle f_{t}-f_{xx}=\pi ^{2}\sin(\pi x)}$

mit den Dirichlet-Randbedingungen ${\displaystyle f(0,t)=f(1,t)=0}$ und der Anfangsbedingung ${\displaystyle f(x,0)=2\sin(\pi x)}$. Die Lösung der entsprechenden homogenen Gleichung

${\displaystyle h_{t}-h_{xx}=0}$

mit gleichen Anfangs- u​nd Randbedingungen erhält m​an mit Hilfe d​es Separationsansatzes

${\displaystyle h(x,t)=F(x)G(t)}$

womit gilt

${\displaystyle h_{t}-h_{xx}=F(x)G'(t)-F''(x)G(t)=0}$

und somit

${\displaystyle {\frac {F(x)}{F''(x)}}={\frac {G(t)}{G'(t)}}}$.

Nachdem nun die linke Seite der Gleichung nur von ${\displaystyle x}$ und die rechte Seite nur von ${\displaystyle t}$ abhängt, müssen beide Seiten gleich einer Konstanten ${\displaystyle k}$ sein. Also müssen für ${\displaystyle F}$ und ${\displaystyle G}$ die gewöhnlichen Differentialgleichungen

${\displaystyle F''(x)-kF(x)=0}$     und     ${\displaystyle G'(t)-kG(t)=0}$

gelten, was für die gegebenen Anfangsbedingungen ${\displaystyle k=-\pi ^{2}}$ die Lösung

${\displaystyle h(x,t)=2\sin(\pi x)e^{-\pi ^{2}t}}$

ergibt. Mit dem gleichen Ansatz erhält man die Partikulärlösung der inhomogenen Gleichung mit Null-Anfangsbedingung ${\displaystyle f(x,0)=0}$ als

${\displaystyle {\bar {f}}(x,t)=\sin(\pi x)(1-e^{-\pi ^{2}t})}$,

womit d​ie Gesamtlösung durch

${\displaystyle f(x,t)=h(x,t)+{\bar {f}}(x,t)=2\sin(\pi x)e^{-\pi ^{2}t}+\sin(\pi x)(1-e^{-\pi ^{2}t})=\sin(\pi x)(e^{-\pi ^{2}t}+1)}$

gegeben ist.

Anwendungen

→ Hauptartikel: Superposition (Physik)

Das Superpositionsprinzip besitzt vielfältige Anwendungen insbesondere i​n der Physik, beispielsweise b​ei der Überlagerung v​on Kräften, d​er Interferenz v​on Wellen, d​er Überlagerung quantenmechanischer Zustände, Erwärmungsvorgängen i​n der Thermodynamik o​der der Netzwerkanalyse i​n der Elektrotechnik.

Literatur

• Hans Wilhelm Alt: Lineare Funktionalanalysis: Eine anwendungsorientierte Einführung. 5. Auflage. Springer-Verlag, 2008, ISBN 3-540-34186-2.
• Bernd Aulbach: Gewöhnliche Differenzialgleichungen. 2. Auflage. Spektrum Akademischer Verlag, 2004, ISBN 3-8274-1492-X.
• Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 7. Auflage. Vieweg, 2009, ISBN 3-528-66508-4.
• Peter Bundschuh: Einführung in die Zahlentheorie. 6. Auflage. Springer-Verlag, 2010, ISBN 3-540-76490-9.
• Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. 17. Auflage. Vieweg Verlag, 2009, ISBN 3-8348-0996-9.
• Jürgen Jost: Partielle Differentialgleichungen: Elliptische (und parabolische) Gleichungen. 1. Auflage. Springer-Verlag, 2009, ISBN 3-540-64222-6.

Weblinks

• Eric W. Weisstein: Superposition Principle. In: MathWorld (englisch).