Induktion (Philosophie)
Induktion (lateinisch inducere ‚herbeiführen‘, ‚veranlassen‘, ‚einführen‘) bedeutet seit Aristoteles den abstrahierenden Schluss aus beobachteten Phänomenen auf eine allgemeinere Erkenntnis, etwa einen allgemeinen Begriff oder ein Naturgesetz.
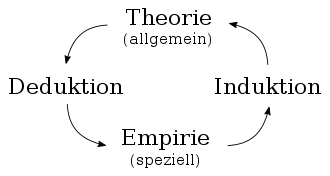
Der Ausdruck wird als Gegenbegriff zu Deduktion verwendet. Eine Deduktion schließt aus gegebenen Voraussetzungen auf einen speziellen Fall, Induktion hingegen ist der umgekehrte Weg. Wie dieser genau zu bestimmen ist, wurde besonders seit Mitte des 20. Jahrhunderts kontrovers diskutiert; ebenso die Frage, ob Induktion und Deduktion tatsächlichen Erkenntnisprozessen im Alltag oder in der Wissenschaft entsprechen oder ob es sich um Artefakte der Philosophie handelt.
David Hume vertrat die Position, dass es eine Induktion im Sinne eines Schlusses auf allgemeine und notwendige Gesetze, der zwingend und erfahrungserweiternd ist, nicht geben kann. Im 20. Jahrhundert haben Theoretiker, wie Hans Reichenbach und Rudolf Carnap, versucht, formal exakte Theorien des induktiven Schließens zu entwickeln. Karl Popper hat vehement zu zeigen versucht, dass Induktion eine Illusion sei,[1] dass in Wirklichkeit immer nur Deduktion zum Einsatz komme und dass sie auch ausreichend sei. Er erhob bis zu seinem Tode den kontroversen Anspruch, mit seinem deduktiven methodologischen Ansatz das Induktionsproblem tatsächlich und endgültig gelöst zu haben.
Im Laufe des 20. Jahrhunderts sind unterschiedliche Versuche unternommen worden, den Begriff der Induktion gegen die Kritik beispielsweise von Hume, Nelson Goodman und Popper zu verteidigen. In diesem Zusammenhang wurden diverse Theorien induktiven Schließens und allgemeinere induktive Methodologien ausgearbeitet (insbesondere mit Rückgriff auf die bayessche Wahrscheinlichkeitslehre) sowie empirische Studien durchgeführt. Fragen, die mit dem Begriff der Induktion zusammenhängen, fallen heute in Teilgebiete der Philosophie des Geistes, der Wissenschaftstheorie, der Logik, der Erkenntnistheorie, der Rationalitäts-, Argumentations- und Entscheidungstheorie, der Psychologie, der Kognitionswissenschaften und der Künstliche-Intelligenz-Forschung.
Das mathematische Verfahren der vollständigen Induktion ist logisch betrachtet kein induktiver Schluss, es handelt sich dabei im Gegenteil um eine deduktive Beweismethode.
Induktionslogik
Induktionslogik befasst sich mit der Frage, ob es ein gültiges Schema gibt, das aus einzelnen Beobachtungen und Fakten auf allgemeine Aussagen schließen lässt. In gültigen deduktiven Argumenten folgt die Konklusion mit Notwendigkeit aus den Prämissen. Induktive Argumente sind hingegen bestenfalls plausibel und gut bestätigt. Zwingend und logisch notwendig, wie deduktive Argumente, sind sie nicht.
|
|
Die Beispiele zeigen Deduktion und Induktion in der traditionellen Form der Syllogistik. Im deduktiven Argument (einem singulären Modus Barbara) wird aus der allgemeinen Aussage „Alle Menschen sind sterblich“ und dem Vorliegen eines Falls dieser Regel „Sokrates ist ein Mensch“ darauf geschlossen, dass die Regel in diesem Fall gilt. Im induktiven Argument hingegen wird eine Beobachtung („Sokrates ist sterblich“) als Fall betrachtet, „Sokrates ist ein Mensch“ und daraus eine allgemeine Aussage abgeleitet. Beim obigen Beispiel kommen sowohl Deduktion als auch Induktion zu einer wahren Konklusion. Die Induktion stellt in diesem Fall aber keinen zwingenden Schluss dar, was das folgende, der logischen Form nach identische Beispiel zeigt:
|
Die Induktion kann also die Zusammenhänge zwischen Begriffen falsch beurteilen. Sobald ein Hund gefunden wird, der kein Dackel ist, ist die Konklusion trotz wahrer Prämissen widerlegt.
Induktive Verallgemeinerung
Es wird von einer Teilklasse auf die Gesamtklasse geschlossen. Die Prämissen dieses Schlusses bestehen darin, dass einerseits eine Teilklasse in einer Gesamtklasse enthalten ist und andererseits alle Elemente der Teilklasse eine gleiche Eigenschaft besitzen. Aus diesen Prämissen wird geschlossen, dass alle Elemente der Gesamtklasse diese Eigenschaft besitzen. Beispiel: Ich beobachte viele Schafe und diese sind alle schwarz. Die Gesamtklasse heißt „Schafe“, die darin enthaltene Teilklasse heißt „von mir beobachtete Schafe“, und die „gleiche Eigenschaft“ heißt „schwarz sein“. Induktive Schlussfolgerung: Alle Schafe sind schwarz. Hier werden viele Schafe als Referenz genommen, um daraus zu schließen, dass alle Schafe schwarz sind, was nicht stimmen muss, da nicht alle Schafe, sondern nur viele beobachtet wurden. Dieses Beispiel verdeutlicht neben dem Vorgang des induktiven Schließens auch seine Mängel. Obwohl diese Schlussweise alltäglich ist – sie ist laut Hume eine Eigenschaft der menschlichen Natur – führt sie unter Umständen zu falschen Schlüssen.
In der logischen Untersuchung des Induktionsschlusses gibt es eine starke Tradition eines wahrscheinlichkeitslogischen Ansatzes. Carnap unterscheidet in seiner Arbeit Induktive Logik und Wahrscheinlichkeit fünf Haupttypen der induktiven Verallgemeinerung:
- direkter Schluss,
- Voraussageschluss,
- Analogieschluss,
- inverser Schluss,
- Allschluss.
Vertreter der Wahrheitsdiskussion wie Popper (1989) oder Hume bezweifeln die Möglichkeit, durch induktive Verallgemeinerung die Wahrheit wissenschaftlicher Hypothesen begründen zu können. Hume war der erste, der sich mit dem Induktionsproblem auseinandergesetzt hat. Er konnte zeigen, dass jeder Versuch einer induktiven Verallgemeinerung einem Zirkelschluss erliegen muss,[2] denn laut Hume stößt man bei jeder induktiven Verallgemeinerung letztlich auf unerlaubte logische Operationen. Das heißt nicht, dass Popper die Zulässigkeit von Verallgemeinerungen leugnen würde, aber er verneint die Möglichkeit, sie mit Einzelaussagen in einen Begründungszusammenhang zu setzen. Diesen scheinbaren Widerspruch versucht Popper letztendlich dadurch zu umgehen, dass er das Begründungsdenken als Ganzes verwirft. Verallgemeinerung sieht nach Popper zwar aus, als sei sie induktiv, funktioniere aber in Wahrheit rein deduktiv, wobei das Aufstellen von unbegründeten, spekulativen Verallgemeinerungen den (Poppers Ansicht nach deduktiv zulässigen) Ausgangspunkt darstellt. Popper verwendet daher den Begriff „Quasi-Induktion“.
Induktiver Teilschluss
Ein wichtiger Fall des Induktionsschlusses besteht darin, dass von einem Teil einer Klasse auf einen anderen Teil dieser Klasse geschlossen wird. Angenommen, es wird festgestellt, dass zwei Arten von Bakterien zu derselben Klasse von Bakterien gehören, und es hat sich herausgestellt, dass die erste Art dieser beiden Klassen auf ein bestimmtes Medikament reagiert. In diesem Fall wird gefolgert, dass auch die zweite Art der Bakterien dementsprechend auf das gleiche Medikament reagiert. Ein Spezialfall dieses Induktionsschlusses liegt vor, wenn von einer Teilklasse einer Klasse auf ein weiteres Element dieser Klasse geschlossen wird.
Induktionsschluss als statistisches Gesetz
Diese Form des Induktionsschlusses liegt dann vor, wenn sich als Resultat der Induktion ein statistisches Gesetz ergibt. Es wird hier von der Wahrscheinlichkeit des Auftretens einer bestimmten Eigenschaft bei den Elementen einer Teilklasse auf die Wahrscheinlichkeit des Auftretens dieser Eigenschaft bei den Elementen der Gesamtklasse geschlossen. Beispiel: Bei der Untersuchung einer Zufalls-Stichprobe von Schülern stellt man fest, dass 4 Prozent unter Legasthenie leiden. Daraus lässt sich schließen, dass vermutlich 4 Prozent aller Schüler an Legasthenie leiden.
Induktive Methoden von John Stuart Mill
John Stuart Mill gilt bis heute als einer der Hauptvertreter des empirisch orientierten Denkens. Da Mill Mitbegründer des Utilitarismus war, wurden seine Stellungnahmen oft nur im Lichte eines „Allinduktionismus“ kritisiert. Für Mill galt die Induktion als methodisches Fundament allen Wissens, das er hauptsächlich mit Methoden zur Untersuchung von einzelnen Kausalzusammenhängen zu analysieren versuchte. Laut Mill ist „die Induktion […] diejenige Verstandesoperation, durch welche wir schließen, daß dasjenige, was für einen besonderen Fall oder besondere Fälle wahr ist, auch in allen Fällen wahr sein wird, welche jenem in irgend einer nachweisbaren Beziehung ähnlich sind“ (Mill, 1980, S. 160). Im Sinne des „Allinduktionismus“ lässt sich laut Mill jedwede Induktion in Form eines Syllogismus darstellen, dessen Obersatz unterdrückt und selbst eine Induktion ist. Die Induktion beruht auf der Neigung des Menschen, Erfahrungen zu generalisieren. Als Voraussetzung für seine Annahmen nennt Mill das Axiom der Induktion, das selbst auch auf einer der allgemeinsten Induktionen basiert und wonach der Gang der Natur absolut gleichförmig ist.
John Stuart Mill beschreibt folgende Methoden zur induktiven Erkenntnisgewinnung (System of Logic, Vol. I, Buch 3, Kapitel 8: „Of the Four Methods of Experimental Inquiry“):
Methode der Übereinstimmung (Method of Agreement)
„Wenn alle Fälle, in denen das untersuchte Phänomen auftritt, nur einen Umstand gemeinsam haben, so ist dieser Umstand eine Ursache (oder Wirkung) des Phänomens.“[3]
| Beispiel: |
|---|
Induktive Schlussfolgerung: Es ist die Beengtheit der Räume, die die Panikattacken verursacht.
Methode des Unterschieds (Method of Difference)
„Wenn eine Situation, in der das untersuchte Phänomen auftritt, und eine andere Situation, in der das untersuchte Phänomen nicht auftritt, bis auf einen einzigen Unterschied völlig gleich sind, ist dieser Unterschied die Wirkung, die Ursache oder ein notwendiger Teil der Ursache des Phänomens.“[4]
| Beispiel: |
|---|
Induktive Schlussfolgerung: Die unabhängige Variable verursacht den Effekt.
Indirekte Methode des Unterschieds (Indirect Method of Difference oder auch Joint Method of Agreement and Difference)
“If two or more instances in which the phenomenon occurs have only one circumstance in common, while two or more instances in which it does not occur have nothing in common save the absence of that circumstance: the circumstance in which alone the two sets of instances differ, is the effect, or cause, or a necessary part of the cause, of the phenomenon.”
„Wenn zwei oder mehr Fälle, in denen das Phänomen auftritt, nur einen Umstand gemeinsam haben, während zwei oder mehr Fälle, in denen es nicht auftritt, nichts gemeinsam haben außer der Abwesenheit dieses Umstandes, dann ist der Umstand, in dem sich die zwei Gruppen unterscheiden, der Effekt, die Ursache oder ein notwendiger Bestandteil der Ursache des Phänomens.“
| Beispiel | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Vier Personen machen ein Picknick, zwei von ihnen werden krank.
Anne (krank) ist im Fluss geschwommen, hat Pudding gegessen, Bier getrunken und war die ganze Zeit in der Sonne. Bertie (krank) ist nicht geschwommen, hat keinen Pudding gegessen und war oft im Schatten, hat aber ebenfalls Bier getrunken. Cecil (gesund): hat sich wie Anne verhalten, hat aber kein Bier getrunken. Dennis (gesund): wie Bertie, hat aber kein Bier getrunken. Das Phänomen ist hier die Erkrankung von Anne und Bertie. Gemeinsam ist ihnen, dass sie Bier getrunken haben. Cecil und Dennis sind jedoch gesund, das Phänomen taucht hier nicht auf. Sie unterscheiden sich von den ersten beiden darin, dass sie kein Bier getrunken haben. Das ist wiederum ein Umstand, den nur Cecil und Dennis gemeinsam haben. | ||||||||||||||||||||||||||||||
|
Induktive Schlussfolgerung: Entweder das Bier wurde wegen der Krankheit konsumiert (Effekt), oder das Bier hat die Krankheit herbeigeführt (Ursache), oder die Krankheit kann ohne Bier nicht auftreten (notwendiger Bestandteil). |
Methode der Residuen (Method of Residues)
“Deduct from any phenomenon such part as is known by previous inductions to be the effect of certain antecedents, and the residue of the phenomenon is the effect of the remaining antecedents.” (deutsch: „Entferne von einem Phänomen jenen Teil, von dem bereits durch frühere Induktionen bekannt ist, dass er die Wirkung bestimmter Ursachen ist; der Rest des Phänomens ist dann die Wirkung der verbleibenden Ursachen.“)
| Beispiel: |
|---|
| Ein Patient hat drei pathologische Auffälligkeiten im Blutbild und drei Symptome. |
| Man weiß bereits, dass zwei der Symptome von zwei der Auffälligkeiten verursacht werden. |
| Induktive Schlussfolgerung: die dritte Auffälligkeit verursacht das dritte Symptom. |
Methode der gleichzeitigen Änderungen (Method of Concomitant Variations)
„Whatever phenomenon varies in any manner whenever another phenomenon varies in some particular manner, is either a cause or an effect of that phenomenon, or is connected with it through some fact of causation.“ (deutsch: „Wenn zwei Phänomene kovariieren, wenn also ein Phänomen sich immer dann verändert, wenn sich ein anderes Phänomen verändert, gibt es zwischen beiden eine Kausalbeziehung.“) Dies ist die Methode der wissenschaftlichen Experimente; hier spricht man von abhängigen und unabhängigen Variablen.
| Beispiel: | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Induktionsproblem
Es ist nicht ohne weiteres klar, weshalb und ob ein Induktionsschluss erlaubt ist. Sehr klar hat diese Frage David Hume erörtert. Hume argumentiert folgendermaßen: Ein Induktionsschluss kann nicht analytisch sein, da hier sonst ein (deduktiver) logischer Schluss vorläge. Logische Schlüsse können aber nicht gehaltsvermehrend sein. Ein Induktionsschluss kann auch nicht synthetisch a priori wahr sein, denn sonst müssten mit seiner Hilfe gefolgerte Sätze ebenso wahr sein. Sie könnten sich dann nicht mehr a posteriori als falsch erweisen. Dies ist aber ein wesentliches Merkmal von auf Erfahrung basierenden Sätzen. Man könnte argumentieren, man wüsste aus Erfahrung, dass der Induktionsschluss funktioniert. Dazu wird entweder ein Induktionsprinzip höherer Ordnung benötigt, die Begründung abgebrochen oder aber ein Zirkelschluss benutzt.
Psychologie
Ohne dass die Diskurse in Philosophie und Psychologie immer scharf zu trennen wären, liegt der Schwerpunkt der Denkpsychologie darauf, welche induktiven Schlüsse Menschen tatsächlich ziehen, ohne Rücksicht darauf, ob diese Schlüsse rational gerechtfertigt sind. Große Akzeptanz genießt die Definition von Philip Johnson-Laird: Induktion ist „jeder Denkprozess, der eine Aussage hervorbringt, die den semantischen Informationsgehalt der ursprünglichen (den Denkprozess auslösenden) Beobachtungen oder Prämissen erhöht“.[5] Demnach ist Induktion die Herstellung von Wissen aus Informationen. Eine wichtige Funktion der Induktion ist nach Johnson-Lairds Definition also die Hypothesenbildung: Der Denkende reduziert seine Unsicherheit, indem er eine Ursache für ein Phänomen oder eine allgemeine Regel vermutet. Dem Denkobjekt wird eine zusätzliche Bedeutung zugeschrieben, die nicht notwendig ist, nur mehr oder weniger plausibel.
Die wichtigste Aufgabe der Induktion ist jedoch die Reduktion der riesigen Datenmenge, die das Gehirn zu verarbeiten hat. Statt jede einzelne Erfahrung mit jedem einzelnen Objekt vorzuhalten (was unmöglich ist – das sogenannte tractability- oder Komplexitäts-Problem), werden ständig vereinfachende Kategorien gebildet und diese projiziert (siehe Schritt 3); nur dadurch ist sinnvolles Verhalten möglich. Beispiel: „Schwere Dinge“ auf „Füße“ – „fallen zu lassen“ – „verursacht“ – „Schmerzen“.
Wird lediglich eine Regel postuliert, ohne nach der Ursache zu fragen („Jeden Morgen geht die Sonne auf“, „Die Ratte drückt einen Hebel häufiger, wenn sie dafür belohnt wird“), spricht man von „deskriptiver Induktion“, wird zusätzlich eine Ursache postuliert, spricht man von „erklärender Induktion“ oder Abduktion.
„Allgemeine Induktion“ bezeichnet den Schluss von mehreren Beobachtungen auf eine Regel (wenn man z. B. glaubt, ein Muster zu erkennen), „spezielle Induktion“ den Schluss von einem Einzelfall auf die Ursache oder eine allgemeine Regel.
Das Induktionsproblem stellt sich in der Psychologie anders dar, da die Frage, was ein Individuum überzeugend findet (vgl. subjektive Wahrscheinlichkeit), ein emotionales und kein formales ist. Während der Eine bereits nach einer einzigen Erfahrung (z. B. mit selbstgepflückten Pilzen) keine weiteren Versuche unternimmt, wird ein Anderer erst nach mehreren Fehlschlägen zur induktiven Schlussfolgerung gelangen, dass die Idee doch nicht so gut war, wie sie zunächst schien.
Beispiele für induktives Denken
Manktelow beschreibt induktives Denken als „das was du tust, wenn du aufgrund von Indizien zu einer Schlussfolgerung gelangst.“[6] Er nennt als typische Beispiele:
- die Arbeit der Kriminalpolizei und der Strafgerichte (Manktelow: „Wenn die Induktion Wahrheit garantieren würde, könnten wir die Richter durch Logiker ersetzen.“)
- die Abschätzung von Häufigkeiten und Wahrscheinlichkeiten, wie „Sieht aus, als ob es morgen regnen würde“; die Diskussionen, ob es eine globale Erwärmung gibt oder ob die (Jugend)kriminalität zunimmt
- die Evolution von Heuristiken.
Für das Problemlösen nennt S. Marshall das Beispiel der Schema-Induktion: Durch wiederholten Umgang mit einem Problemtyp (zum Beispiel Rekursions-Aufgaben) kann man ein Lösungsschema induzieren und auf neue Probleme vom selben Typ anwenden.[7]
Ein Spezialfall des induktiven Denkens ist das induktive Schlussfolgern. Hierfür nennen Eysenck und Keane als wichtigen Zweck die Vorhersage: Begegnet man einem Objekt, das man als „Hund“ klassiert, kann man daraus induktiv schließen „könnte beißen“.[8] Unsere Vorfahren mussten also nicht jeden einzelnen Bären im Wald kennen: Wer einen Begriff „Bär“ besaß, der die Eigenschaft „gefährlich“ enthielt, konnte sich arterhaltend verhalten.
Ablauf einer Induktion
Eine Induktion besteht aus folgenden Arbeitsschritten:
- Mustererkennung (Voraussetzung für eine Induktion): Im Strom der Wahrnehmungen oder in anderen Datenpools Regelmäßigkeiten bemerken. Beispiel 1 (für einen Begriff): Ich finde einen Smaragd, er ist grün. Ich finde einen anderen Smaragd, auch er ist grün usw. Beispiel 2 (für eine Regel): Gestern morgen ging die Sonne auf, vorgestern morgen ging die Sonne auf,...
- Kategorisierung oder Begriffsbildung (die eigentliche Induktion): Das erkannte Muster in einer Aussage zusammenfassen. Beispiel 1: Smaragde sind grün. Beispiel 2: Jeden Morgen geht die Sonne auf.
- Projektion (nutzbringende Anwendung einer Induktion, fakultativ): Die so gefundene Proposition auf nicht beobachtete Objekte (an entlegenen Orten oder in der Vergangenheit oder Zukunft) ausdehnen. Beispiel 1: Alle zukünftig und an anderen Orten gefundenen Smaragde werden grün sein. Beispiel 2: Auch morgen wird die Sonne wieder aufgehen.
Diese sogenannte „aufzählende“ Methode der Induktion ist seit Aristoteles bekannt und beruht auf einer Verallgemeinerung von Einzelfällen. In der englischsprachigen Literatur wird sie daher instance based genannt.
Zu beachten ist, dass die Induktion von Begriffen (z. B. Kategorien) und Regeln nicht von Individuen selbstständig erarbeitet wird, sondern vom sozialen Kontext, insbesondere von der Erziehung, massiv beeinflusst wird. So wurde in einem Experiment zwei Gruppen von Kleinkindern, die jünger als ein Jahr waren und noch nicht sprechen konnten, je fünf Stoffkatzen gegeben. Einer Gruppe sagte man immer wieder, dass dies „Katzen“ seien, der anderen Gruppe sagte man nichts. Nach einer Weile gab man beiden Gruppen noch eine Stoffkatze und einen Stoffbären und stellte fest, dass die Kinder der ersten Gruppe sich deutlich häufiger mit dem Bären beschäftigten, während die Kinder der zweiten Gruppe mit beiden neuen Puppen gleich häufig spielten. Dieses Resultat wurde so interpretiert: Den Kindern der ersten Gruppe wurden von den Erwachsenen ein Name für alle fünf Gegenstände genannt, wodurch sie angeregt wurden, nach gemeinsamen Eigenschaften zu suchen. Der Bär, der diese gemeinsamen Eigenschaften nicht alle aufwies, wurde als etwas Neues erkannt.
Spezielle Induktionsschlüsse
Nicht immer bedarf es des mehrfachen Auftretens eines Phänomens, um daraus Schlussfolgerungen abzuleiten. Im Alltag ist es häufig notwendig, Rückschlüsse aus einer einzelnen Beobachtung zu ziehen:
Mein Zeh schmerzt, nachdem ich den Schuh angezogen habe. Induktion: Im Schuh ist ein Steinchen.
Wie in diesen Beispielen handelt es sich dabei meist um Abduktionen: Aus dem mitgebrachten Wissen, dass ein Auto nicht anspringt, wenn die Batterie leer ist (und dass leere Batterien häufiger sind als defekte Anlasser o. ä.), ziehe ich als plausibelsten Schluss, dass wohl die Batterie leer sein wird.
Wer sich daran einmal den Magen verdorben hat, wird vielleicht nie wieder Muscheln essen. Und wer die gleiche Erfahrung häufiger macht, wird seine Schlüsse bestätigt finden und zunehmend verfestigen. Die Motivation und die Erfahrung spielen also eine große Rolle beim induktiven Schließen. Werden solche Schlüsse unzulässig verallgemeinert und von anderen übernommen, können Vorurteile entstehen.
Das Ergebnis einer Induktion muss nicht eine Kategorie, ein Begriff oder eine Regel sein. Neue Informationen können auch dazu führen, dass alte Regeln gelockert werden. Diese regelbasierte Induktionsmethode wurde besonders in der KI-Forschung untersucht. Das klassische Beispiel: Jahrhundertelang war man in Europa überzeugt, Schwäne seien große Wasservögel aus der Familie der Enten, mit langem Hals usw. und weißem Gefieder. Die neue Information aus Australien, dass es auch schwarze Schwäne gibt, führte zu dem Induktionsschluss, dass die bekannte Regel zu lockern sei und nun lauten müsse, Schwäne seien große Wasservögel aus der Familie der Enten, mit langem Hals usw.
Glaubwürdigkeit
Wie überzeugend ein Induktionsschluss wirkt, hängt von mehreren Faktoren ab. Bei der Induktion durch Verallgemeinerung hat die Anzahl der zusammengefassten Einzelfälle (auch Stichprobengröße genannt) einen wesentlichen Einfluss: je mehr Beispiele eine Hypothese untermauern, umso mehr Vertrauen kann ich in sie setzen. Beispiel: Ich lerne einen Angolaner kennen, der ausgesprochen höflich ist. Ich lerne einen zweiten Angolaner kennen, der ebenfalls sehr höflich ist usw. In mir formt sich das (Vor-)Urteil: Angolaner sind höflich. Gegenbeispiele (ich lerne auch unhöfliche Angolaner kennen) können mich dazu bringen, mein Urteil abzuschwächen („Fast alle/die meisten/viele Angolaner sind höflich“, sogenannte subjektive Wahrscheinlichkeit) oder ganz zu verwerfen („Angolaner sind nicht höflicher als andere Menschen“).
Ein weiteres Kriterium für die Glaubwürdigkeit eines Induktionsschlusses ist die Variabilität der Referenzklasse. Referenzklasse ist der kleinste gemeinsame Oberbegriff der in Rede stehenden Einzelfälle. Ist jemand überzeugt, dass die Mitglieder einer Referenzklasse einander sehr ähnlich sind (geringe Variabilität), genügen wenige Beobachtungen, um diese zu verallgemeinern. Wenn die Referenzklasse jedoch sehr verschiedenartige Individuen umfasst (hohe Variabilität), sind viele Einzelbeobachtungen nötig, bevor ein allgemeines Urteil gerechtfertigt erscheint. In der Statistik nennt man diese Eigenschaft Repräsentativität. Beispiel: Eine neue Pflanzenart wurde entdeckt, und die ersten gefundenen Exemplare trugen alle süß schmeckende rote Beeren. Der induktive Schluss, dass andere Exemplare sich nicht anders fortpflanzen werden, wirkt bereits nach wenigen Einzelbeobachtungen hoch wahrscheinlich. Anders ist dies jedoch bei der Größe der Pflanzen: selbst wenn die ersten Exemplare alle kleiner als 20 cm waren, besteht doch die Möglichkeit, dass die Pflanze bei anderen Licht- und Bodenbedingungen größer wird. Hier wären deutlich mehr Funde nötig, und zwar an möglichst verschiedenen Standorten, bis die Induktion „Diese Pflanzenart wird nicht größer als 20 cm“ überzeugt.
Dieses letzte Beispiel zeigt, dass die beobachteten Einzelphänomene möglichst das ganze Feld des induzierten Begriffes überdecken sollten. Beispiel: Die Information, dass Frau A. weder Rotbarsch noch Hering, Zander, Barsch, Forelle, Scholle, Heilbutt usw. isst, lässt nicht die Schlussfolgerung zu, Frau A. sei Vegetarierin. Trotz der vielen verschiedenen Einzelfälle fehlt es an Überdeckung. Erst wenn bekannt wird, dass sie auch kein Rind, Schwein, Geflügel, Wild usw. isst, ist der Begriff „Vegetarierin“ ausreichend abgedeckt und die Induktion glaubwürdig.[9]
Induktion in den Sozialwissenschaften
Das Schema der Induktion lautet allgemein: Prämissen: „Z Prozent der F sind G“ und „x ist F“, Konklusion: „x ist G – aber nur mit Z Prozent Wahrscheinlichkeit“.
Liegt der Wert von Z nahe bei 100 % oder 0 %, hat man es mit starken Argumenten zu tun. Im ersten Fall: „x ist G“, im zweiten Fall: „x ist nicht G“. Liegt der Z-Wert nahe bei 50 %, ist die Konklusion schwach, weil beide Argumente gleichermaßen unterstützt werden.
In den Sozialwissenschaften ist letzteres häufig der Fall. Vielfach muss man sich in den Sozialwissenschaften mit „Teils-Teils-Aussagen“ begnügen. Das Ziel, allgemein gültige Gesetze des sozialen Verhaltens abzuleiten, wird zugunsten einer „quantifizierenden“ Darstellung aufgegeben.
| Beispiel: |
|---|
Die Frage, mit der sich auch die Sozialwissenschaften auseinandersetzen müssen: „Wie sind induktive Allsätze möglich?“ bzw. „Wie können aus einzelnen Beobachtungen allgemein gültige Gesetze („Allsätze“) abgeleitet werden?“, ist nicht zufriedenstellend zu beantworten.
Der Ausweg aus dem Dilemma wird in den Sozialwissenschaften auf zweierlei Wegen gesucht. Die deduktiv-nomologischen Wissenschaftler der analytischen Wissenschaftstheorie beziehen sich auf die „Poppersche Wende“ des Falsifikationismus: Deduktion statt Induktion. Die Wissenschaftler der phänomenologischen/hermeneutischen Methode verzichten weitestgehend auf die Formulierung von Allsätzen, die raum-zeitlich unbegrenzt sind, zugunsten eines subjektiven interpretativen-historischen Verfahrens und begnügen sich mit raum-zeitlich begrenzten Aussagen (Theorie mittlerer Reichweite).
Induktive Schlüsse haben einen heuristischen Wert. Ein gültiges Induktionsschema, das es gestattet, von wahren Prämissen auf wahre Konklusionen zu schließen, ist logisch ausgeschlossen und nur mit metaphysischen Annahmen möglich.
Induktion in der Künstlichen Intelligenz
In der Künstlichen Intelligenz befasst sich u. a. das PI-Modell (Processes of Induction, 1986) von Holland, Holyoak und Mitarbeitern mit der Induktion. In diesem Modell werden die durch Induktion gefundenen Regeln eingeteilt in statische, zeitlose, Zustände beschreibende Regeln (synchronic rules) und solche, die Veränderungen beschreiben (diachronic rules). Die synchronischen Regeln lassen sich wiederum unterteilen in klassenbildende Regeln (categorical rules) und in gedächtnisaktivierende Regeln (associative rules). Die diachronischen Regeln sind entweder vorhersagend (predictor rules) oder legen die Reaktion auf einen Reiz fest (effector rules). Alle diese Regeln sind hierarchisch geordnet, es gibt übergeordnete allgemeine und untergeordnete spezielle Regeln.
| Beispiele: | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
Literatur
Allgemein
- S. A. Gelman, J. R. Star, J. E. Flukes: Children’s use of generics in inductive inference. In: Journal of Cognition and Development 3 (2002), 179–199.
- S. A. Gelman, E. M. Markman: Categories and induction in young children. In: Cognition 23 (1986), 183–209.
- S. A. Gelman: The development of induction within natural kind and artifact categories. In: Cognitive Psychology 20 (1988), 65–95.
- M. L. Gick, K. J. Holyoak: Schema induction and analogical transfer. In: Cognitive Psychology 15 (1983), 1–38
- E. Heit, J. Rubinstein: Similarity and property effects in inductive reasoning. In: Journal of Experimental Psychology: Learning. Memory, and Cognition 20 (1994), 411–422.
- J. H. Holland, K. J. Holyoak, R. E. Nisbett, P. R. Thagard (Hrsg.): Induction: Processes of inference, learning, and discovery. Cambridge, MA: Bradford Books/MIT Press 1986.
- Kayoko Inagaki, Giyoo Hatano: Conceptual and Linguistic Factors in Inductive Projection: How Do Young Children Recognize Commonalities between Animals and Plants? in: Dedre Gentner, Susan Goldin-Meadow (Hrsg.): Language in Mind, Advances in the Study of Language and Thought, MIT Press 2003, 313–334
- Keith J. Holyoak, Robert G. Morrison (Hrsg.): The Cambridge Handbook of Thinking and Reasoning, CUP 2005, versch. Kapitel, v. a. 13–36 und 117–242
- P. N. Johnson-Laird: Human and machine thinking. Hove, 1993
- T. K. Landauer, S. T. Dumais: A solution to Plato’s problem: The latent semantic analysis theory of acquisition, induction, and representation of knowledge. In: Psychological Review 104 (1997), 211–240.
- Ken Manktelow: Reasoning and Thinking. Psychology Press: Hove (GB) 1999
- Gregory L. Murphy: The Big Book of Concepts. MIT Press 2002, v. a. Kap. 8: Induction, 243–270
- N. Ross, D. Medin, J. D. Coley, S. Atran: Cultural and experimental differences in the development of folkbiological induction. In: Cognitive Development 18 (2003), 25–47.
- S. A. Sloman: Feature-based induction. In: Cognitive Psychology 25 (1993), 231–280.
- E. E. Smith: Concepts and Induction. In: M. Posner (Hrsg.): Foundations of Cognitive Science. MIT Press, Cambridge 1989.
Philosophiegeschichte
- J. R. Milton: Induction before Hume. British Journal for the Philosophy of Science 38 (1987), 49–74.
- Jaakko Hintikka: On the Development of Aristotle’s Ideas of Scientific Method and the Structure of Science. In: William Wians (Hrsg.): Aristotle’s Philosophical Development: Problems and Prospects, Rowman and Littlefield, Lanham, Maryland 1996, 83–104.
- Ders.: The Concept of Induction in the Light of the Interrogative Approach to Inquiry. In: John Earman (Hrsg.): Inference, Explanation, and Other Frustrations, University of California Press, Berkeley 1993, 23–43.
Logik und Wissenschaftstheorie
- Alexander Bird: Philosophy of Science, London: UCL Press 1998, Kap. 5 und 7,Leichtverständliche Einführung
- Rudolf Carnap: Logical Foundations of Probability, Chicago, IL: University of Chicago Press 2. A. 1962.Klassische Ausarbeitung einer Theorie des Induktionsschlusses.
- A. F. Chalmers: What is this Thing Called Science? Open University Press, 3. A. 1999, Kap. 4–6.Sehr leichtverständliche Einführung
- Martin Curd, John A. Cover (Hrsg.): Philosophy of Science: The Central Issues, W. W. Norton & Co. 1998, insb. 412–432, 495–508.Wichtige klassische Aufsätze oder Auszüge und neuere Überblicksartikel
- Nelson Goodman: Fact, Fiction and Forecast, Indianapolis, In: Hackett Publishing Company, 1955 (3. A. 1979).Klassische Formulierung des sog. neuen Induktionsproblems
- Jaakko Hintikka: Inquiry as Inquiry: A Logic of Scientific Discovery, Kluwer Academic, Dordrecht 1999.Eigenwilliger Lösungsvorschlag.
- P.N. Johnson-Laird: A model theory of induction. International Studies in the Philosophy of Science 8 (1994)
- Mark Kaplan: Epistemic Issues in Induction. In: Routledge Encyclopedia of Philosophy
- Philip Kitcher: The Naturalists Return. In: The Philosophical Review 101 (1992), 53–114.Naturalistischer Lösungsvorschlag.
- Peter Lipton: Inference to the Best Explanation, Routledge, London 1991.Moderner Klassiker.
- Patrick Maher: Inductive Inference. In: Routledge Encyclopedia of Philosophy
- John D. Norton: A Material Theory of Induction (PDF; 161 kB), in: Philosophy of Science 70 (2003), 647–670.
- Wesley C. Salmon: Inductive Inference. In: B. Baumrin (Hrsg.) Philosophy of Science: The Delaware Seminar. New York: Interscience Publishers, 353-70. Klassische Verteidigung der pragmatischen Lösung
- Steven A. Sloman, David A. Lagnado: The Problem of Induction. In: Keith J. Holyoak, Robert G. Morrison: The Cambridge Handbook of Thinking and Reasoning, CUP 2005, 95–116
- Wolfgang Stegmüller: Das Problem der Induktion: Humes Herausforderung und moderne Antworten. In: H. Lenk (Hrsg.) Neue Aspekte in der Wissenschaftstheorie, Braunschweig 1971 Diskussion der Positionen von Hume, Carnap und Popper; Bestätigungstheorie als Nachfolgeproblem des Induktionsproblems
- Richard Swinburne (Hrsg.): The Justification of Induction, Oxford University Press, Oxford 1974.
- Jonathan Vogel: Inference to the best explanation. In: Routledge Encyclopedia of Philosophy
Sozialwissenschaften
- Andreas Diekmann (Hrsg.): Methoden der Sozialforschung, Kölner Zeitschrift für Soziologie und Sozialpsychologie, Sonderheft 44/2004
Weblinks
- Brad Armendt, Martin Curd: Probability and Induction, Bibliographie
- Interpretations of Probability. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- Gilbert Harman, Sanjeev R. Kulkarni: The Problem of Induction (PDF; 180 kB), 2005
- James Hawthorne: Inductive Logic. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- Franz Huber: Confirmation and Induction. In: J. Fieser, B. Dowden (Hrsg.): Internet Encyclopedia of Philosophy.
- Patrick Maher: Seminar in Philosophy of Science, Lecture Notes zu einem Einführungsseminar mit Schwerpunkt auf induktiver Logik
- John D. Norton: A Little Survey of Induction (MS Word; 99 kB), vorauss. in: P. Achinstein (Hrsg.): Scientific Evidence: Philosophical and Historical Perspectives
- Samir Okasha: What did Hume really show about induction?, in: The Philosophical Quarterly 51 (2001), 307–327
- William Talbott: Bayesian Epistemology. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- John Vickers: The Problem of Induction. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Einzelnachweise
- Vgl. exemplarisch: Karl R. Popper, David W. Miller: A proof of the impossibility of inductive probability. In: Nature 302 (1983), 687–688
- Logik der Forschung, Abschnitt 1
- im Original: „If two or more instances of the phenomenon under investigation have only one circumstance in common, the circumstance in which alone all the instances agree, is the cause (or effect) of the given phenomenon.“
- im Original: „If an instance in which the phenomenon under investigation occurs, and an instance in which it does not occur, have every circumstance in common save one, that one occuring only in the former: the circumstance in which alone the two instances differ, is the effect, or cause, or a necessary part of the cause, of the phenomenon.“
- im Original: „Induction is any process of thought yielding a conclusion that increases the semantic information in its initial observations or premises.“
- Manktelow, s. Literaturliste; im Original: what you do when you arrive at a conclusion on the basis of some evidence
- Sandra P. Marshall: Schemas in problem solving. Cambridge University Press 1995.
- Michael W. Eysenck, Mark T. Keane: Cognitive Psychology. Psychology Press, Hove (UK), 2000.
- D. N. Osherson u. a. (1990): Category-based induction. Psychological Review, 97