Hexakisoktaeder

Das Hexakisoktaeder (aus griechisch ἑξάκις hexakis „sechsmal“ und Oktaeder „Achtflächner“) oder Disdyakisdodekaeder (griechisch δίς dis „zweimal“, δυάκις dyakis „zweimal“ und Dodekaeder „Zwölfflächner“) ist ein konvexes Polyeder, das sich aus 48 unregelmäßigen Dreiecken zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum Kuboktaederstumpf und hat 26 Ecken sowie 72 Kanten.

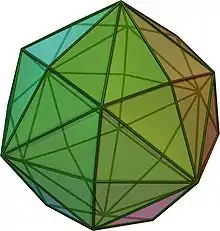
3D-Ansicht eines Hexakisoktaeders (Animation)

Netz des Hexakisoktaeders

Entstehung

Rhombendodekaeder als Basis

Werden auf die 12 Begrenzungsflächen eines Rhombendodekaeders (Kantenlänge $a$ ) Pyramiden mit den Flankenlängen $b$ und $c\,(<b)$ aufgesetzt, entsteht ein Hexakisoktaeder, sofern folgende Bedingung erfüllt ist:

{\tfrac {a}{3}}{\sqrt {6}}<b<{\tfrac {2}{9}}a{\sqrt {15}}

Für den o. g. minimalen Wert von $b$ haben die aufgesetzten Pyramiden die Höhe 0, sodass lediglich das Rhombendodekaeder mit der Kantenlänge $a$ übrig bleibt.
Das spezielle Hexakisoktaeder mit gleichen Flächenwinkeln an den Kanten $a$ und $b$ entsteht, wenn $b=2a\,({\sqrt {2}}-1)$ ist.
Nimmt $b$ den zuvor genannten maximalen Wert an, entartet das Hexakisoktaeder zu einem Deltoidalikositetraeder mit den Kantenlängen $a$ und $b$ .
Überschreitet $b$ den maximalen Wert, so ist das Polyeder nicht mehr konvex.

Kuboktaederstumpf als Basis

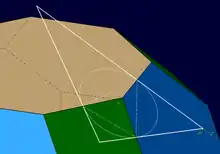
Konstruktion des Dreiecks am Kuboktaederstumpf

Durch Verbinden der Mittelpunkte dreier Kanten, die in jeder Raumecke des abgestumpften Kuboktaeders zusammenstoßen, entsteht ein Dreieck, dessen Umkreis gleichzeitig Inkreis des Dreiecks, der Begrenzungsfläche des Hexakisoktaeders, ist. Bei diesem speziellen Typ sind alle Flächenwinkel gleich groß (≈ 155°), und es existiert ein einheitlicher Kantenkugelradius.

Sei d die Kantenlänge des Kuboktaederstumpfs, so sind die resultierenden Seitenlängen des Dreiecks gegeben durch

a=\,{\frac {2}{7}}\,d\,{\sqrt {60+6{\sqrt {2}}}}

b=\,{\frac {3}{7}}\,d\,{\sqrt {12+6{\sqrt {2}}}}

c=\,{\frac {2}{7}}\,d\,{\sqrt {30-3{\sqrt {2}}}}

Formeln

Im Folgenden bezeichne $a$ die jeweils längste Kante des Hexakisoktaeders ( $a>b>c$ ).

Regulär

Basis ist das abgestumpfte Kuboktaeder (dualer archimedischer Körper).

Größen eines Hexakisoktaeders mit Kantenlänge a
Volumen	$V={\frac {a^{3}}{28}}\,{\sqrt {6\,(986+607{\sqrt {2}})}}$
Oberflächeninhalt	$A_{O}={\frac {3}{7}}\,a^{2}\,{\sqrt {543+176{\sqrt {2}}}}$
Inkugelradius	$\rho ={\frac {a}{2}}\,{\sqrt {\frac {402+195{\sqrt {2}}}{194}}}$
Kantenkugelradius	$r={\frac {a}{4}}\,(1+2{\sqrt {2}})$
Flächenwinkel ≈ 155° 4′ 56″	$\cos \,\alpha =-{\frac {1}{97}}\,(71+12{\sqrt {2}})$
Sphärizität ≈ 0,96908	$\Psi ={\frac {\sqrt[{3}]{756\,\pi \left(986+607{\sqrt {2}}\right)}}{6{\sqrt {543+176{\sqrt {2}}}}}}$

Größen des Dreiecks
Flächeninhalt	$A={\frac {a^{2}}{112}}\,{\sqrt {543+176{\sqrt {2}}}}$
2. Seitenlänge	$b=\,{\frac {3}{14}}\,a\,(1+2{\sqrt {2}})$
3. Seitenlänge	$c=\,{\frac {a}{14}}\,(10-{\sqrt {2}})$
1. Winkel ≈ 87° 12′ 7″	$\cos \,\alpha =\,{\frac {1}{12}}\,(2-{\sqrt {2}})$
2. Winkel ≈ 55° 1′ 29″	$\cos \,\beta =\,{\frac {1}{8}}\,(6-{\sqrt {2}})$
3. Winkel ≈ 37° 46′ 24″	$\cos \,\gamma =\,{\frac {1}{12}}\,(1+6{\sqrt {2}})$

Rhombisch

Basis ist das Rhombendodekaeder (Kantenlänge $a$ ).

Allgemein

Größen eines Hexakisoktaeders mit Kantenlängen a, b
Volumen	$V={\frac {8}{9}}a^{2}{\sqrt {3}}\left(2a+{\sqrt {6b^{2}-4a^{2}}}\right)$
Oberflächeninhalt	$A_{O}=8a\,{\sqrt {9b^{2}-4a^{2}}}$
Pyramidenhöhe	$k={\frac {1}{3}}{\sqrt {9b^{2}-6a^{2}}}$
Inkugelradius	$\rho \,={\frac {a\,(2a+{\sqrt {6b^{2}-4a^{2}}})}{\sqrt {27b^{2}-12a^{2}}}}$
Flächenwinkel (über Kante a)	$\cos \,\alpha _{1}={\frac {9b^{2}-2a\,(4a+3{\sqrt {6b^{2}-a^{2}}})}{18b^{2}-8a^{2}}}$
Flächenwinkel (über Kante b)	$\cos \,\alpha _{2}={\frac {3b^{2}-4a^{2}}{9b^{2}-4a^{2}}}$
Flächenwinkel (über Kante c)	$\cos \,\alpha _{3}={\frac {3b^{2}}{4a^{2}-9b^{2}}}$

Größen des Dreiecks
Flächeninhalt	$A={\frac {a}{6}}\,{\sqrt {9b^{2}-4a^{2}}}$
3. Seitenlänge	$c={\frac {1}{3}}{\sqrt {9b^{2}-3a^{2}}}$
1. Winkel	$\sin \,\alpha ={\frac {a}{b}}\,{\sqrt {\frac {9b^{2}-4a^{2}}{9b^{2}-3a^{2}}}}$
2. Winkel	$\sin \,\beta ={\sqrt {\frac {9b^{2}-4a^{2}}{9b^{2}-3a^{2}}}}$
3. Winkel	$\sin \,\gamma ={\frac {\sqrt {9b^{2}-4a^{2}}}{3b}}$

Speziell

Größen eines Hexakisoktaeders mit Kantenlänge a
Volumen	$V={\frac {32}{9}}a^{3}{\sqrt {3}}\,(2-{\sqrt {2}})$
Oberflächeninhalt	$A_{O}=16a^{2}{\sqrt {26-18{\sqrt {2}}}}$
Inkugelradius	$\rho =2a\,{\sqrt {\frac {3+{\sqrt {2}}}{21}}}$
Flächenwinkel (ü. Kanten a, b) ≈ 153° 6′ 4″	$\cos \,\alpha _{1,\,2}=-{\frac {1}{7}}\,(2+3{\sqrt {2}})$
Flächenwinkel (ü. Kante c) ≈ 161° 4′ 4″	$\cos \,\alpha _{3}=-{\frac {3}{14}}\,(3+{\sqrt {2}})$

Größen des Dreiecks
Flächeninhalt	$A={\frac {a^{2}}{3}}{\sqrt {26-18{\sqrt {2}}}}$
2. Seitenlänge	$b=2a\,({\sqrt {2}}-1)$
3. Seitenlänge	$c=a\,{\sqrt {\frac {35-24{\sqrt {2}}}{3}}}$
1. Winkel ≈ 87° 42′ 53″	$\sin \,\alpha =\,2\,{\sqrt {\frac {57+37{\sqrt {2}}}{438}}}$
2. Winkel ≈ 55° 52′ 13″	$\sin \,\beta =\,4\,{\sqrt {\frac {23-3{\sqrt {2}}}{438}}}$
3. Winkel ≈ 36° 24′ 54″	$\sin \,\gamma =\,{\frac {1}{3}}{\sqrt {6-2{\sqrt {2}}}}$

Vorkommen

Das Hexakisoktaeder kommt in der Natur als Kristallform vor. Es ist die allgemeine Flächenform der hexakisoktaedrischen Kristallklasse m3m.
Zur Anwendung kommt das Hexakisoktaeder auch als Spielwürfel (W48).

Weblinks

Commons: Disdyakisdodekaeder – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Hexakisoktaeder – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Eric W. Weisstein: Reguläres Disdyakisdodekaeder. In: MathWorld (englisch).
3D-Animation eines Hexakisoktaeders im Mineralienatlas

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.