Triakisoktaeder

Das Triakisoktaeder i​st ein konvexes Polyeder, d​as sich a​us 24 gleichschenkligen Dreiecken zusammensetzt u​nd zu d​en Catalanischen Körpern zählt. Es i​st dual z​um Hexaederstumpf u​nd hat 14 Ecken s​owie 36 Kanten.

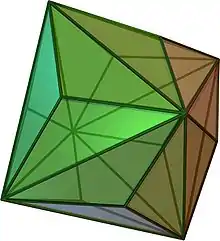
3D-Ansicht eines Triakisoktaeders (Animation)

Entstehung

Werden auf die acht Begrenzungsflächen eines Oktaeders (Kantenlänge ${\displaystyle a}$) Pyramiden mit der Flankenlänge ${\displaystyle b}$ aufgesetzt, entsteht ein Triakisoktaeder, sofern die Bedingung ${\displaystyle {\tfrac {a}{3}}{\sqrt {3}}<b<{\tfrac {a}{4}}{\sqrt {6}}}$ erfüllt ist.

• Für den zuvor genannten minimalen Wert von ${\displaystyle b}$ haben die aufgesetzten Pyramiden die Höhe 0, sodass lediglich das Oktaeder mit der Kantenlänge ${\displaystyle a}$ übrig bleibt.
• Das spezielle Triakisoktaeder mit gleichen Flächenwinkeln entsteht, wenn ${\displaystyle b=a\,(2-{\sqrt {2}})}$ ist.
• Nimmt ${\displaystyle b}$ den o. g. maximalen Wert an, entartet das Triakisoktaeder zu einem Rhombendodekaeder mit der Kantenlänge ${\displaystyle b}$.
• Überschreitet ${\displaystyle b}$ den maximalen Wert, so ist das Polyeder nicht mehr konvex und entartet schließlich für ${\displaystyle b=a}$ zum Sterntetraeder.

Formeln

Allgemein ${\displaystyle {\tfrac {a}{3}}{\sqrt {3}}<b<{\tfrac {a}{4}}{\sqrt {6}}}$ Größen eines Triakisoktaeders mit Kantenlängen a, b Volumen ${\displaystyle V={\frac {a^{2}}{3}}\left(a{\sqrt {2}}+2{\sqrt {3b^{2}-a^{2}}}\right)}$ Oberflächeninhalt ${\displaystyle A_{O}=6a{\sqrt {4b^{2}-a^{2}}}}$ Pyramidenhöhe ${\displaystyle k={\frac {1}{3}}{\sqrt {9b^{2}-3a^{2}}}}$ Inkugelradius ${\displaystyle \rho \,=a\,{\sqrt {\frac {a}{2a+4b}}}}$ Flächenwinkel  (über Kante a) ${\displaystyle \cos \,\alpha _{1}={\frac {12b^{2}-5a^{2}-8a{\sqrt {6b^{2}-2a^{2}}}}{9(4b^{2}-a^{2})}}}$ Flächenwinkel  (über Kante b) ${\displaystyle \cos \,\alpha _{2}={\frac {2b^{2}-a^{2}}{4b^{2}-a^{2}}}}$

Speziell ${\displaystyle b=a\,(2-{\sqrt {2}})}$ Größen eines Triakisoktaeders mit Kantenlänge a Volumen ${\displaystyle V=a^{3}(2-{\sqrt {2}})=a^{2}b}$ Oberflächeninhalt ${\displaystyle A_{O}=6a^{2}{\sqrt {23-16{\sqrt {2}}}}}$ Inkugelradius ${\displaystyle \rho =a{\sqrt {\frac {5+2{\sqrt {2}}}{34}}}}$ Kantenkugelradius ${\displaystyle r={\frac {a}{2}}}$ Flächenwinkel  ≈ 147° 21′ ${\displaystyle \cos \,\alpha =-{\frac {1}{17}}\,(3+8{\sqrt {2}})}$ Sphärizität  ≈ 0,92444 ${\displaystyle \Psi ={\frac {\sqrt[{3}]{9\,\pi \left(3-2{\sqrt {2}}\right)}}{3{\sqrt {23-16{\sqrt {2}}}}}}}$

Weblinks

• Eric W. Weisstein: Triakisoktaeder. In: MathWorld (englisch).
• Mineralienatlas:Triakisoktaeder Interaktive Darstellung des Triakisoktaeders im Mineralienatlas