Planimeter
Ein Planimeter (seltener: Integrator) ist ein mathematisches Instrument und ein Analogrechner, also ein mechanisches Messgerät, zur Ermittlung beliebiger Flächeninhalte in Landkarten oder Zeichnungen. Man fährt den Rand der zu messenden Fläche mit einem Fahrstift oder einer Lupe mit Fadenkreuz o. ä. entlang, wobei ein Messrad die Fläche integriert. Der Rand ist eine geschlossene Kurve, Anfangs- und Endpunkt der Messfahrt ist derselbe. Das Vorzeichen der Messung wird dadurch bestimmt, ob der Rand im Uhrzeiger- oder Gegenuhrzeigersinn abgefahren wird.

Die zu messenden Flächen können fast beliebige Form haben (unregelmäßige Polygone, andere unregelmäßige Flächen, Höhenlinien oder Grundstücke), müssen aber stetige und stückweise glatte Ränder haben. Die ganze Fläche muss in der Reichweite des Fahrarmes liegen, d. h. einen Durchmesser haben, der kleiner ist als das Doppelte der Fahrarmlänge (meist 20–30 cm). Die Genauigkeit liegt bei typischerweise zirka 1 ‰, bei speziellen Geräten auch höher.
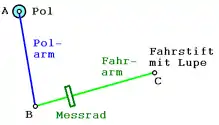

Das Polarplanimeter
Es gibt verschiedene Arten von Planimetern wie Polarplanimeter, Scheiben- und Rollenplanimeter, von denen das erstere am meisten verbreitet ist.
Das Polarplanimeter wurde 1854 vom Schaffhauser Ingenieur und Unternehmer Jakob Amsler-Laffon erfunden.
Das Gerät hat einen festen Pol, der in die Nähe der zu messenden Fläche gesetzt wird. Dann fährt man den Rand der Fläche möglichst genau ab, was zum Beispiel auf Landkarten oder Katasterplänen mit Ungenauigkeiten von etwa 0,1 bis 0,3 mm möglich ist.
Funktionsprinzip
Die mechanische Konstruktion von Planimetern beruht auf einem Prinzip von Leonhard Euler, das der bekannte Mathematiker für die Berechnung infinitesimaler Flächen entwickelt hat, sowie auf dem Satz von Green.
Eulers Prinzip besagt, dass eine infinitesimale Fläche aus einem infinitesimalen Parallelogramm plus einer infinitesimalen Dreiecksfläche zusammensetzbar ist. Die Dreiecksfläche wiederum besteht aus einem (endlichen) Radius sowie einem infinitesimalen Winkel.
Im Planimeter werden nun während der Umfahrung der Fläche mit dem Messstift oder einer Messlupe mit Fadenkreuz die kleinen Winkel fortlaufend aufsummiert (integriert). Entscheidend bei diesem Vorgang ist, dass axiale Verschiebungen der Rolle (d. h. Verschiebungen in Richtung der Drehachse) auf der Planunterlage idealerweise keinen Einfluss auf die Drehung der Rolle haben (sozusagen perfekter Schlupf in axialer Richtung).
An einer Skala, die mit einem Nonius oder einer anderen optischen Einrichtung zur Erhöhung der Ablesegenauigkeit versehen ist, kann der Flächeninhalt direkt abgelesen werden.


Anpassungen und Genauigkeit
Die an der Rolle abgelesene Maßzahl der Fläche ist insbesondere auch proportional zur Länge des Fahrarms. Durch Verstellung der Fahrarmlänge kann ein Planimeter also an verschiedene Maßeinheiten (Quadratzentimeter, square inch, …) oder an verschiedene Zeichnungs-Maßstäbe angepasst werden. Die Ungenauigkeit bei dieser Einstellung geht aber direkt ins Endergebnis ein. Manche Planimeter sind mit einem Fahrarm verstellbarer Länge mit entsprechender Einstellskala versehen, manche mit einem Fahrarm fixer Länge.
Die Genauigkeit der Flächenbestimmung kann innerhalb gewisser Grenzen noch gesteigert werden, indem man die zu bestimmende Fläche vergrößert und nach der Planimetrierung das Resultat durch das Quadrat des linearen Vergrößerungsfaktors dividiert.
Anwendung
Die Anwendung des Verfahrens ist nur durch die Baugröße des Planimeters beschränkt. Bei sehr großen Flächen kann man jedoch den Pol in deren Mitte setzen (Verfahren „Pol innen“), womit sie fast 4-mal so groß sein kann wie beim normalen Modus „Pol außen“.
Des Weiteren wurden Planimeter in deutlich größeren Ausführungen gefertigt. Z. B. wurden in der Lederfertigung zur Bestimmung der Fläche von Tierhäuten ca. 1,5 Meter große Planimeter eingesetzt[1].
Es gibt auch Spezialplanimeter zur Bestimmung des statischen Moments, des Trägheitsmoments oder höherer Momente beliebiger Flächen (sogenannte Momentenplanimeter). Diese wurden zum Beispiel im Schiffbau bei der Auslegung von Dampfmaschinen und Dieselmotoren eingesetzt, um die maschinenbedingten Schlingerbewegungen des Schiffes zu minimieren.
Auch im Eisenbahn- und Straßenbau kamen Momentenplanimeter zur Berechnung der Auf- und Abträge von Bodenmaterial zum Einsatz[2].
Literatur
- Jakob Amsler: Über die mechanische Bestimmung des Flächeninhaltes, der statischen Momente und der Trägheitsmomente ebener Figuren, insbesondere über einen neuen Planimeter. Vierteljahresschrift der naturforschenden Gesellschaft Zürich, Schaffhausen 1856
- Alfred Amsler: Ueber den Flächeninhalt und das Volumen durch Bewegung erzeugter Curven und Flächen und über mechanische Integration. Meier, Schaffhausen, 1880
- Robert Amsler, Theodor H. Erismann: Jakob Amsler-Laffon 1823–1912, Alfred Amsler 1857–1940. Pioniere der Prüfung und Präzision. Verein für wirtschaftshistorische Studien, Meilen 1993, ISBN 3-909059-04-X
- Joachim Fischer: 200 Jahre Planimeter – Ein bayerischer Vermesser und seine geniale Idee (1814–2014) (über Johann Martin Hermann, u. a.). Ausstellungskatalog (171 S., mit DVD). Eine Ausstellung des Landesamtes für Digitalisierung, Breitband und Vermessung in Zusammenarbeit mit Joachim Fischer, dem Deutschen Museum und dem Bayerischen Hauptstaatsarchiv. München 2014
- Andreas Galle: Mathematische Instrumente. Teubner, Leipzig 1912
- Felix Klein: Elementarmathematik vom Höheren Standpunkte aus, Teil II: Geometrie. Vorlesung gehalten im Sommersemester 1908. Ausgearbeitet von E. Hellinger. Teubner, Leipzig 1909, S. 22–31
- Hermann Pieper: Der Oldenburgsche Planimeter. Herold und Wahlstab, Lüneburg 1825 (Digitalisat)
- Henry Selby Hele-Shaw: The Theory of Continuous Calculating Machines. In: Philosophical Transactions of the Royal Society, Part II, Bd. 176 (1885), S. 367–402
- Simon Stampfer: Über das neue Planimeter des Caspar Wetli. In: Zeitschrift des österreichischen Ingenieur-Vereins, Band 11, Nr. 7, Wien 1850
- William Thomson (Lord Kelvin): Mechanical Integration of the General Linear Differential Equation of any Order with Variable Coefficients (Paper VI). In: Proceedings of the Royal Society, Bd. 24 (1876), S. 271–275
- Friedrich Adolf Willers: Mathematische Maschinen und Instrumente. Akademie-Verlag, Berlin 1951
Weblinks
Einzelnachweise
- G. Coradi: Anleitung zum Gebrauch des Ledermessers von G. Coradi. Zürich 6, ca. 1913, 2 Seiten, Bedienungsanleitung.
- Jacob Amsler: Anwendung des Integrators (Momentenplanimeters) zur Berechnung des Auf- und Abtrages bei Anlage von Eisenbahnen, Straßen und Canälen. Orell Füssli & Co., Zürich, 1875.