Statik starrer Körper

Die Statik starrer Körper (auch Starrkörperstatik, Stereostatik oder Stereo-Statik genannt) ist ein Teil der Starrkörpermechanik und der Statik. Sie behandelt das Gleichgewicht von Kräften an starren Körpern, also an nicht verformbaren Körpern. In der Statik bewegen sich diese Körper entweder mit konstanter Geschwindigkeit oder sie ruhen. Bedeutung hat die Starrkörperstatik als Teilgebiet der Technischen Mechanik zur Berechnung von Kräften, die in Bauteilen wirken. Die Starrkörperstatik behandelt die Grundlagen der Technischen Mechanik; weiterführende Gebiete sind die Elastostatik, die Dynamik und die Baustatik.

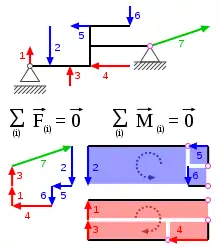
Balkenkonstruktion mit Fest- und Loslager und erfüllten Gleichgewichtsbedingungen (Summe aller Kräfte und Momente gleich null)

Im Rahmen der Starrkörperstatik werden viele Themen abgehandelt, die in anderen Gebieten der Mechanik ebenfalls von Bedeutung sind. Die Gleichgewichtsbedingungen sind in der gesamten Statik gültig, Grundbegriffe wie Kraft, Moment, Flächenschwerpunkt und Massenschwerpunkt sind in der gesamten Mechanik verbreitet, während Lagerungen, Kraftsysteme, Schnittprinzip und Schnittreaktionen in der gesamten Technischen Mechanik eine Rolle spielen. Die Modellvorstellung des starren Körpers und das Linienflüchtigkeitsaxiom gelten in der gesamten Starrkörpermechanik.

Definition, Einordnung, Abgrenzung und Verhältnis zu angrenzenden Gebieten

Definition

Die Statik wird als Teilgebiet der Mechanik definiert, bei dem sich die Kräfte im Gleichgewicht[1] befinden und in ihrer Wirkung folglich aufheben, oder alternativ als „Lehre von Körpern, die sich in Ruhe befinden“, also von unbewegten Körpern.[2] Da sich auch Körper, die sich mit konstanter Geschwindigkeit bewegen, im Gleichgewicht befinden, lassen sich diese auch mit den Methoden der Statik behandeln.

Ein starrer Körper ist ein physikalischer Körper, der sich nicht verformen kann. Die Statik starrer Körper behandelt somit das Gleichgewicht an diesen Körpern.

Einordnung

Die Statik in der Technischen Mechanik

Strukturierung der Mechanik unter dem
Gesichtspunkt der beteiligten Kräfte

Mechanik

Kinematik
Bewegungsgesetze
ohne Kräfte

Dynamik
Wirkung von
Kräften

Statik
Kräfte im Gleichgewicht
ruhender Körper

Kinetik
Kräfte verändern den
Bewegungszustand

Da die Statik Teil der Mechanik ist, ist die Starrkörperstatik sowohl Teil der Starrkörpermechanik als auch der allgemeinen Statik zu der neben der Starrkörperstatik unter anderem auch die Fluidstatik (Für Gase und Flüssigkeiten) und die Elastostatik (für elastische Körper) zählen. Die Einordnung der Statik erfolgt jedoch in der Physik und den Ingenieurwissenschaften unterschiedlich.

In der Physik wird die Mechanik eingeteilt in die Kinematik, die sich mit Ort, Geschwindigkeit und Beschleunigung von Körpern befasst, aber nicht mit Kräften oder Massen, sowie in die Dynamik, die Kräfte und Massen berücksichtigt. Die Dynamik lässt sich weiter unterteilen in die Statik für Körper, bei denen sich die Kräfte im Gleichgewicht befinden, und in die Kinetik, die sich mit den Körpern befasst, an denen sich die Kräfte nicht im Gleichgewicht befinden. De facto[3] wird die Statik in der Physik nicht gesondert behandelt und der Technischen Mechanik überlassen. Die beiden Physiker Joseph Honerkamp, Hartmann Römer schreiben dazu: Die Berechnung von Zwangskräften ist ein technisch sehr wichtiges Problem; man kann beispielsweise die Ingenieurstatik geradezu als Lehre von der Berechnung von Zwangskräften ansehen.[4]

Die Technische Mechanik wird gegliedert in die Statik, die Festigkeitslehre und die Dynamik. De facto wird in Lehrbüchern und -veranstaltungen unter „Statik“ neben einigen Grundlagen einer allgemeinen Statik (z. B. Gleichgewichtsbedingungen) die Statik starrer Körper abgehandelt,[5] Gebiete wie Elastostatik oder Baustatik werden explizit als solche bezeichnet. Da es für deformierbare Körper eigenständige Disziplinen gibt, versteht man unter Statik im engeren Sinne häufig nur die Statik starrer Körper.[6] Innerhalb des Bauingenieurwesens ist mit Statik jedoch häufig die statische Berechnung gemeint oder die Baustatik, die auch deformierbare, feste Körper behandelt. Die Festigkeitslehre als weiteres Gebiet der Technischen Mechanik behandelt dagegen ausschließlich deformierbare Körper.[7][8]

Abgrenzung und Verhältnis zu angrenzenden Gebieten

Die Festigkeitslehre befasst sich mit allen deformierbaren, festen Körpern, die sich im Gleichgewicht befinden. Sie geht für den Fall Statisch bestimmter Systeme meist (in der Theorie I. Ordnung) davon aus, dass die wirkenden Kräfte mit den Methoden der Starrkörperstatik ermittelt wurden und baut insofern auf dieser auf. Mit den bekannten Kräften kann anschließend untersucht werden wie stark sich ein Bauteil verformt. Über die räumliche und flächige Verteilung dieser Kräfte in den Bauteilen (Mechanische Spannung), die für die Festigkeitslehre von besonderer Bedeutung sind, kann die Starrkörperstatik aber keine Aussagen machen. Die Körper müssen dann als deformierbar betrachtet werden, ebenso bei Stabilitätsproblemen (Knicken, Beulen) und bei statisch unbestimmten Systemen.[9]

In der Kinetik sind die wirkenden Kräfte nicht im Gleichgewicht. Diese befinden sich aber mit den Trägheitskräften (keine Kräfte im Sinne der Newtonschen Mechanik) im sogenannten dynamischen Gleichgewicht. Die Berechnung dynamischer Systeme (starrer Körper) lässt sich dann durchführen mit Methoden der (Starrkörper-)Statik. Insofern baut die Kinetik auf der Statik auf.[10][11] Die Statik, die mit den Methoden der Starrkörperstatik auskommt, wird daher in Vorlesungen und Lehrbüchern der Technischen Mechanik praktisch immer zuerst abgehandelt.

Anwendungsbereiche

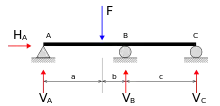
Beispiel für ein statisch unbestimmtes System

Ziel der Statik als Teil der Technischen Mechanik ist es im Wesentlichen, die Kräfte zu berechnen, die in einzelnen Bauteilen wirken. Dies gelingt mit der Statik starrer Körper nur bei sogenannten statisch bestimmten Systemen. Bei diesen reichen die Gleichgewichtsbedingungen aus, um die Kräfte zu berechnen. Bei statisch unbestimmten Systemen werden weitere Bedingungen benötigt; die Gleichgewichtsbedingungen der Statik starrer Körper bleiben aber gültig. Statisch unbestimmte Systeme werden im Gebiet der Festigkeitslehre[12] und der Baustatik[13] abgehandelt.

Themenüberblick

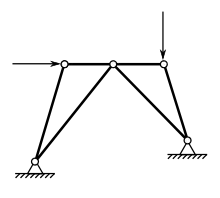
Ein Fachwerk aus sechs Stäben mit zwei Kräften. Die oberen drei kleinen Kreise symbolisieren Drehgelenke, die unteren sind unverschiebliche (Fest-)Lager, in denen sich die Stäbe ebenfalls drehen können.

In den Lehrbüchern der Technischen Mechanik gibt es große Einigkeit darüber, welche Themengebiete zur Starrkörperstatik zählen, lediglich die Reihenfolge variiert. Die Kraft als zentrale Größe wird oft zu Beginn eingeführt. Manchmal wird gleich im Anschluss das eng verwandte Moment (Kraft mal Hebelarm) eingeführt,[14] häufig jedoch erst, wenn es für die allgemeinen Kraftsysteme benötigt wird.[15] Kraftsysteme erlauben es, mehrere Kräfte zu einer Resultierenden zusammenzufassen, einzelne Kräfte aufzuspalten in mehrere Kräfte (vor allem solche, die parallel zu Koordinatenachsen sind), das Überprüfen, ob sich mehrere Kräfte im Gleichgewicht befinden und das Berechnen unbekannter Kräfte, sofern sich die Kräfte im Gleichgewicht befinden.

Lager sind Bauteile, durch die Körper mit ihrer Umgebung verbunden werden. Durch sie wirken Kräfte auf die betrachteten Körper ein. Diese Kräfte treten erst dann hervor, wenn die Lager in Gedanken entfernt und durch diese Kräfte ersetzt werden. Dieses Ersetzen wird als Freischneiden bezeichnet.

Reale Maschinen und Bauwerke bestehen häufig aus mehreren Teilen, die zusammengesetzt werden. Diese können an jeder beliebigen Stelle (z. B. an den Fügestellen) in Gedanken freigeschnitten und in mehrere Teilsysteme zerlegt werden (Schnittprinzip), um so die unbekannten Kräfte zu berechnen. Zu diesen Systemen zählen sämtliche Tragwerke. Kräfte oder Momente im Inneren von Körpern werden als Schnittgrößen bezeichnet. Sie werden in der Festigkeitslehre benötigt, lassen sich aber mit der Statik starrer Körper berechnen, falls die Körper statisch bestimmt gelagert sind.

Weitere Themen sind Reibung und Schwerpunkte (geometrischer Schwerpunkt und Massenschwerpunkt). Zur Reibung zählt auch die Haftreibung bei unbewegten Körpern und die Gleitreibung für bewegte Körper. Die Berechnung von Schwerpunkten wird benötigt, um die Wirkungslinie von resultierenden Kräften zu bestimmen, insbesondere falls die Kräfte auf Volumen, Flächen oder Linien verteilt wirken wie Druckkräfte (Fläche) oder Gewichtskräfte (Volumen).

Axiome der Starrkörperstatik

Die Statik basiert auf Axiomen, also Annahmen, die nicht bewiesen werden können, die jedoch mit Erfahrungen mit realen Körpern in Einklang stehen. Im Gegensatz zu den Newtonschen Axiomen besteht über die Axiome der Statik weder in ihrer Reihenfolge noch ihrer Anzahl ein Konsens.[16] Folgende Axiome werden in der Literatur genannt; viele sind nicht nur in der Starrkörperstatik gültig, sondern in der Statik oder Mechanik allgemein, andere gelten hingegen nur für die gesamte Starrkörpermechanik:

Gleichgewichtsaxiom: Zwei Kräfte, die auf einen starren Körper wirken, stehen genau dann im Gleichgewicht, wenn sie gleichen Betrag und Wirkungslinie haben und in entgegengesetzte Richtung zeigen. Es geht zurück auf Pierre de Varignon.[17]

Für deformierbare Körper gilt dies nur, falls die beiden Kräfte am selben Punkt angreifen. Wenn sie nur auf derselben Wirkungslinie liegen, können sie ihn stauchen oder strecken. Falls sie nicht auf derselben Wirkungslinie liegen, drehen sie einen frei beweglichen Körper, ohne den Schwerpunkt zu verschieben. Sie bilden dann ein sogenanntes Kräftepaar.[18][19]

Wechselwirkungsaxiom: Wenn eine Kraft von einem Körper auf einen anderen Körper wirkt, dann übt dieser auf den ersten eine Kraft aus, die auf derselben Wirkungslinie liegt, den gleichen Betrag hat und der ersten Kraft entgegengerichtet ist.

Dies gilt für sämtliche Körper, nicht nur für starre Körper und auch für Kräfte im Inneren von Körpern.[20]

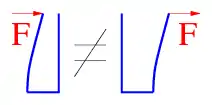
Bei einem deformierbaren Körper gilt das Linienflüchtigkeitsaxiom nicht.

Linienflüchtigkeitsaxiom (auch Verschiebungssatz,[21] Verschiebungsgesetz[22] oder Längsverschiebungssatz:[23]) Eine Kraft, die auf einen starren Körper einwirkt, darf entlang ihrer Wirkungslinie verschoben werden, ohne dass sich die Wirkung (Beschleunigung) auf den Körper ändert.

Dies gilt in der gesamten Starrkörpermechanik. Bei gleicher Wirkungslinie und gleicher Richtung macht es also für das Gleichgewicht und die Beschleunigung an einem starren Körper keinen Unterschied, ob eine Kraft an ihm vorne zieht oder ihn hinten drückt. Für deformierbare Körper macht dies jedoch einen Unterschied und ebenso für die Kräfte im Inneren beliebiger (also auch starrer) Körper (Schnittkräfte). Es gilt somit, dass Körper immer zuerst freigeschnitten werden und erst danach Kräfte verschoben werden dürfen. Eine Verschiebung einer Kraft auf eine parallele Wirkungslinie darf dagegen nur durchgeführt werden, wenn das Versatzmoment berücksichtigt wird.[24]

Axiom vom Kräfteparallelogramm: Zwei Kräfte, die an einem gemeinsamen Punkt angreifen, können durch eine resultierende Kraft ersetzt werden, die sich als Diagonale des Parallelogrammes ergibt, das von den beiden Kräften aufgespannt wird.

Das gilt auch für den Spezialfall, dass sie auf derselben Wirkungslinie liegen. Das Parallelogramm entartet dann zu einer Strecke.

Überlagerungssatz: Zwei Kräfte, die sich im Gleichgewicht befinden, können einer Gruppe von Kräften hinzugefügt werden, ohne die Wirkung auf den starren Körper zu ändern.[25]

Der Satz gilt in der gesamten Mechanik starrer Körper. Mit Wirkung ist das Gleichgewicht und die Beschleunigung des Körpers gemeint, Schnittgrößen ändern sich im Allgemeinen durch Hinzufügen von Gleichgewichtsgruppen.

Grundbegriffe

Die wichtigsten Grundbegriffe sind der starre Körper, die Kraft, das Moment und der Freiheitsgrad.

Starrer Körper

Ein starrer Körper ist ein theoretischer Körper, der sich unter der Wirkung von Kräften nicht verformt. In der Realität gibt es zwar keine starren Körper, da sich jeder Körper verformt. Bei vielen praktischen Problemstellungen sind diese Verformungen jedoch so klein, dass mit dem Modell des starren Körpers gute Ergebnisse erzielt werden können.[26] Das Modell wird auch in der Dynamik genutzt.

Kraft

Die Kraft ist eine physikalische Größe, die einen ruhenden Körper in Bewegung zu setzen versucht. Wichtige Kräfte in der Technischen Mechanik sind die Gewichtskraft und die Reibungskraft einschließlich der Haftreibung. Kräfte werden in der Mechanik mathematisch als Vektor modelliert und durch einen Pfeil dargestellt. Sie sind durch mehrere Bestimmungsstücke definiert:[27]

Ihren Betrag, dargestellt als Länge des Pfeiles.
Ihren Angriffspunkt, dargestellt als Fuß oder Anfangspunkt des Pfeiles.
Ihre Wirkungslinie, in Zeichnungen meist nicht dargestellt. Sie ergibt sich als Gerade durch Fußpunkt und Spitze des Pfeiles.
Ihren Richtungssinn, also die Richtung entlang der Wirkungslinie

Richtungssinn und Wirkungslinie werden auch zur Richtung zusammengefasst.[28] In der Starrkörpermechanik kann der Angriffspunkt auch weggelassen werden.

Im Allgemeinen ist die Kraft ein punktgebundener Vektor, der sich auf den Angriffspunkt bezieht. In der Statik starrer Körper können Kräfte jedoch entlang ihrer Wirkungslinien verschoben werden (solange sie auf denselben Starrkörper wirken); es handelt sich somit um einen linienflüchtigen Vektor.

Kräfte werden in der Mechanik nach verschiedenen Kriterien eingeteilt.[29]

Verschiedene Belastungen

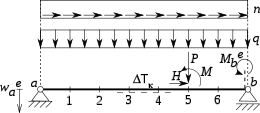
Nach der räumlichen Verteilung unterscheidet man:

Einzelkräfte oder Punktkräfte, Einzellast oder Einzelmoment die auf einen einzelnen Punkt einwirken. Es handelt sich um eine Idealisierung; reale Kräfte wirken immer auf Flächen oder Volumen verteilt. Die Gewichtskraft wird häufig als Einzelkraft modelliert, die im Schwerpunkt angreift.
Eine Linienkraft oder Streckenlast ist auf eine Linie verteilt. Es handelt sich ebenfalls um Idealisierungen.
Eine Flächenkraft, Flächenlast oder Oberflächenspannung wirkt auf eine Fläche, beispielsweise wirken Druckkräfte von Flüssigkeiten auf Behälterwände oder Winde auf Gebäude. Häufig sind Flächenkräfte in einer oder mehreren Dimensionen konstant. Wenn von Körpern nur der Querschnitt betrachtet wird, werden aus Flächenkräften Streckenlasten.
Volumenkräfte wirken auf das ganze Volumen eines Körpers ein. Dazu zählt vor allem die Gewichtskraft.

Nach der Ursache wird unterschieden zwischen:

Eingeprägte Kraft: Sie hat eine physikalische Ursache wie die Gewichtskraft oder der Winddruck.
Reaktionskraft: Sie reagiert auf äußere Einflüsse, z. B. die Kraft, die im Fundament eines Bauwerkes seiner Gewichtskraft entgegenwirkt. Zu den Reaktionskräften zählen insbesondere auch die Lagerkraft und die Zwangskraft, die die Bewegungsmöglichkeiten von Körpern einschränken.

Nach ihrer Wirkung wird unterschieden zwischen der

Nahkraft, die nur wirkt, wenn sich die beiden Körper, zwischen denen sie wirkt, in direktem Kontakt befinden und der
Fernkraft, die auch über Entfernungen hinweg wirken kann, wie die Gravitation oder elektrische und magnetische Kräfte.

Nahkräfte sind normalerweise Flächenkräfte, die über die Kontaktfläche übertragen werden. Fernkräfte sind normalerweise Potentialkräfte, die in der Kontinuumsmechanik als Volumenkräfte angesetzt werden.

Nach dem Wirkungsort wird unterschieden in die

äußere Kraft, die von außen auf einen Körper einwirkt und die
innere Kraft, die im Inneren eines Körpers wirkt. Dazu zählen die sogenannten Schnittgrößen.[30]

Moment

Kraft um einen Bezugspunkt

Kräftepaar

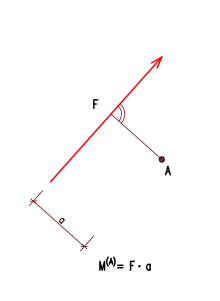
Das Moment ist eine physikalische Größe, die einen Körper zu drehen versucht. In der Technischen Mechanik wird unterschieden zwischen dem Moment einer (einzelnen) Kraft bezüglich eines Punktes und dem Moment eines Kräftepaares (ohne Bezugspunkt). Das Moment $M^{(A)}$ einer einzelnen Kraft $F$ ist nur in Bezug auf einen beliebig wählbaren Punkt $A$ definiert. Sein Betrag lässt sich berechnen aus dem senkrechten Abstand $a$ der Wirkungslinie dieser Kraft zum Bezugspunkt und dem Betrag $F$ der Kraft zu

M^{(A)}=F\cdot a

.

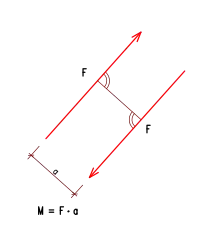
Ein Kräftepaar besteht aus zwei Kräften, die den gleichen Betrag $F$ haben, auf parallelen Wirkungslinien liegen mit dem Abstand $a$ und in entgegengesetzte Richtung zeigen. Ein Kräftepaar kann einen Körper nicht verschieben wie eine Kraft, es versucht ihn jedoch zu drehen. Der Betrag des Momentes $M$ , das von dem Kräftepaar ausgeübt wird, ergibt sich aus dem Abstand und dem Betrag einer der beiden Kräfte zu

M=F\cdot a

.

Das Moment eines Kräftepaares hat keinen Bezugspunkt und wirkt in der gesamten Ebene, in der die beiden Kräfte liegen. In der Mechanik starrer Körper kann es durch sein Moment ersetzt werden falls keine Schnittgrößen von Interesse sind aber nicht durch eine resultierende Kraft. Eine einzelne Kraft dagegen kann nicht durch ihr Moment ersetzt werden.[31][32]

Freiheitsgrade eines starren Körpers

Ein Freiheitsgrad eines Körpers ist eine Bewegungsmöglichkeit, die dieser prinzipiell hat. Ein starrer Körper, der sich nur innerhalb einer Ebene bewegen kann, kann in zwei Dimensionen verschoben werden, und er kann gedreht werden. Somit verfügt er über drei Freiheitsgrade. Drehungen werden auch als Rotationen bezeichnet und Verschiebungen als Translationen. Ein starrer Körper, der sich im dreidimensionalen Raum bewegen kann, hat insgesamt sechs Freiheitsgrade: In jeder Dimension ist eine Rotation und eine Translation möglich. Deformierbare Körper haben darüber hinaus noch Freiheitsgrade der Verformung, also unendlich viele.[33]

Lager

Bauteile, durch die die betrachteten Körper mit ihrer Umgebung verbunden sind, werden als Lager bezeichnet. Die Art und Weise, wie ein Körper gelagert ist, wird als Lagerung bezeichnet. Lager erlauben manche Bewegungen und unterbinden andere.

Die Lager einer Tür beispielsweise, die als Starrkörper auf einer starren lochspielfreien Lagerung idealisiert wird, erlauben ausschließlich eine Drehung und verhindern alle anderen Bewegungen. Die Lager der meisten Schubladen, die als Starrkörper auf einer lochspielfreien idealen unverschieblichen Lagerung idealisiert werden, erlauben dagegen ausschließlich eine Verschiebung und unterbinden sämtliche Drehungen. Die Anzahl der Freiheitsgrade, die ein Lager unterbindet, wird als seine Wertigkeit bezeichnet. Die Lager der Tür und der Schublade sind somit fünfwertig, da sie von den sechs prinzipiell möglichen Bewegungen fünf verhindern.

Lager können fest mit der Umgebung verbunden sein (Festlager), oder sie sind selbst verschieblich (Loslager). Eine Brücke beispielsweise, die nur an ihren Enden gelagert ist, wird üblicherweise mit einem Festlager und mehreren Loslagern ausgestattet. Wenn sie sich durch Temperaturänderung ausdehnt, kann sie sich praktisch unbehindert in horizontaler Richtung, sowohl in Längs- als auch in Breitenrichtung, bewegen, weil die Loslager die Bewegung im Allgemeinen mit einem vernachlässigbaren Widerstand zulassen.

Für die zahlreichen Lager gibt es in der Technischen Mechanik entsprechende Symbole. Besonders häufig sind Lager, die Drehungen erlauben, da diese herstellungstechnisch meist einfacher sind. Diese werden durch einen kleinen Kreis dargestellt.

Die drei häufigsten Symbole in ebenen Tragsystemen:

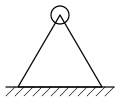Symbol für ein Festlager
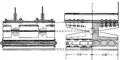Konstruktionszeichnung eines Loslagers auf Rollen
Reales Loslager
Symbol für ein Loslager
Zeichnung eines fest eingespannten Balkens in Galileis Discorsi
Symbol für feste Volleinspannung (eingespannter vertikaler Balken)

Lager können durch verschiedene Bauteile realisiert werden. Für Details siehe Lager (Bauwesen) und Lager (Maschinenelement).[34]

Schnittprinzip

Beispiel einer Welle

Ein gerader Balken (durchgezogene Linie), von zwei Seiten geschnitten, mitsamt den freigeschnittenen Kräften und Momenten. Die gestrichelte Linie ist die Bezugsfaser und dient zur Verdeutlichung positiver Richtungen.

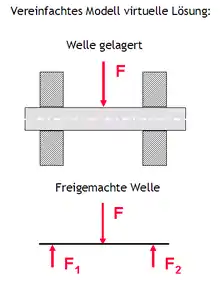
Die auf einen Körper einwirkenden Kräfte werden mit Ausnahme der Fernkräfte über angrenzende Körper (insbesondere Lager) eingeleitet. Um diese Kräfte für Berechnungen zugänglich zu machen, wird eine Methode angewandt, die Schnittprinzip genannt wird. Der Vorgang wird als Freischneiden oder Freimachen bezeichnet. Dabei werden Körper in Gedanken ersetzt durch die Kräfte, die sie übertragen. Besondere Bedeutung hat das Schneiden der Lager, die durch ihre Lagerreaktionen ersetzt werden. Lager, die Verschiebungen verhindern, werden durch Kräfte ersetzt (Lagerkraft) und Lager, die Drehungen verhindern, durch Momente (Einspannmoment).

Grundsätzlich kann jeder Körper an jeder beliebigen Stelle geschnitten werden. Die Schnittstellen werden in Zeichnungen durch geschwungene Linien verdeutlicht, sofern nicht die Lager freigeschnitten werden. Wenn beispielsweise ein Körper an einem Seil hängt, kann der Körper durch seine Gewichtskraft ersetzt werden und das Seil in Gedanken geschnitten werden, wodurch die Seilkraft erscheint, die der Gewichtskraft entgegenwirkt.[34][35]

Kraftsysteme

Ein Kraftsystem oder eine Kraftgruppe ist eine Reihe von Kräften, die in einem System wirken: beispielsweise sämtliche Kräfte, die auf eine Brücke wirken, alle, die auf ein Fahrzeug wirken oder nur die, die auf das Getriebe wirken. Bei freigeschnittenen Systemen zählen zu den Kräften auch die Schnittkräfte. Kräftesysteme erlauben mehrere Operationen. Dazu zählt die Zusammenfassung von mehreren Kräften zu einer Resultierenden und die Ermittlung von unbekannten Kräften über die Gleichgewichtsbedingungen. Damit lässt sich überprüfen, ob zwei verschiedene Kraftsysteme statisch äquivalent sind, also dieselbe Wirkung auf einen Körper haben. Weiters lässt sich überprüfen, ob sich ein Kraftsystem im Gleichgewicht befindet. Mit der Annahme, dass es sich im Gleichgewicht befindet, lassen sich die unbekannten Kräfte berechnen.

Kraftsysteme werden nach zwei verschiedenen Kriterien eingeteilt. Nach der Anzahl der Dimensionen unterscheidet man zwischen ebenen und räumlichen Kraftsystemen. Nach dem Vorkommen von Momenten unterscheidet man zwischen zentralen Kraftsystemen (ohne Momente), bei denen sich die Wirkungslinien aller Kräfte in einem einzigen Punkt schneiden, und allgemeinen Kraftsystemen (mit Momenten), bei denen sich die Kräfte nicht in einem einzigen Punkt schneiden.[36]

Zusammenfassen und Aufteilen von Kräften

Kräfteparallelogramm

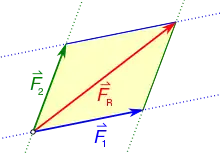
Zwei Kräfte mit gemeinsamem Angriffspunkt lassen sich mittels des Kräfteparallelogramms zu einer Resultierenden zusammenfassen, die die gleiche Wirkung hat wie die Einzelkräfte. Mehr als zwei Kräfte mit gemeinsamem Angriffspunkt lassen sich zusammenfassen, indem zunächst von zwei Kräften eine Resultierende gebildet und der Vorgang dann wiederholt wird. Umgekehrt kann eine einzelne Kraft in mehrere Komponenten zerlegt werden, die in vorgegebene Richtungen zeigen (beispielsweise Koordinatenachsen).

Kräfte, bei denen sich die Wirkungslinien in einem gemeinsamen Punkt schneiden, können ebenfalls mit dem Kräfteparallelogramm zusammengefasst werden. Sie werden dazu zunächst entlang ihrer Wirkungslinien in den Schnittpunkt verschoben und dort zusammengefasst. Entsprechend funktioniert auch eine Zerlegung.

Falls sich die Wirkungslinien nicht in einem einzigen Punkt schneiden, lassen sich die Kräfte zusammenfassen, indem sie in einen Punkt verschoben werden. Bei der Parallelverschiebung auf eine andere Wirkungslinie entsteht dabei ein Versatzmoment, das berücksichtigt werden muss. Das System aus resultierender Kraft und dem Gesamtmoment wird als Dyname bezeichnet. Durch Parallelverschiebung der resultierenden Kraft lässt sich das Moment beseitigen. Damit stehen Betrag, Richtung und Wirkungslinie der resultierenden Kraft fest.

Ein Spezialfall ist das Kräftepaar. Es lässt sich nicht zu einer resultierenden Kraft zusammenfassen, aber es lässt sich ersetzen durch sein Moment (ohne resultierende Kraft).[37]

Gleichgewicht

Ein Körper befindet sich im Gleichgewicht, wenn die resultierende Kraft und das resultierende Moment bezüglich eines beliebigen Punktes jeweils null ergeben. In einem ebenen Kräftesystem, das genau eine horizontale und genau eine vertikale Richtung aufspannt, bedeutet dies:

Die Summe aller Kraftkomponenten in horizontaler Richtung beträgt null.
Die Summe aller Kraftkomponenten in vertikaler Richtung beträgt null.
Die Summe aller Momente in der Ebene bezüglich eines beliebigen Punktes beträgt null.

Im räumlichen Kraftsystem ergeben sich je Dimension ein Kräftegleichgewicht und ein Momentengleichgewicht. Die Kräftegleichgewichte gelten in allen beliebigen Richtungen.

Mit diesen Gleichgewichtsbedingungen lässt sich für eine Reihe bekannter Kräfte überprüfen, ob sie im Gleichgewicht sind. Ist bekannt, dass sich ein Körper nicht bewegt, und ist nur ein Teil der Kräfte bekannt, lassen sich mit den Gleichgewichtsbedingungen die unbekannten Kräfte berechnen. Da im ebenen Fall nur drei unabhängige Gleichungen aufgestellt werden können, lassen sich für einen einzelnen Körper mit den Methoden der Starrkörperstatik nur drei Unbekannte berechnen. Im räumlichen Fall ergeben sich dementsprechend sechs Gleichungen und Unbekannte für einen einzelnen Körper.

Falls weitere Kräfte unbekannt sind, werden weitere Gleichungen benötigt, die dann Verformungen und Werkstoffkennwerte enthalten. Diese sind Gegenstand der Baustatik und der Festigkeitslehre. Bei mehreren Körpern, die zu einem größeren Körper verbunden sind (beispielsweise Einzelteilen, die zu Baugruppen und Modulen zusammengefügt sind), lässt sich für jeden Starrkörper eine entsprechende Anzahl Unbekannter berechnen (drei in der Ebene).[38]

Systeme starrer Körper

Ein Gerberträger: Er besteht aus drei Balken, die mit zwei Gelenken (kleine Kreise) verbunden sind. Links befindet sich ein Festlager (Dreieck), in der Mitte und rechts befinden sich insgesamt drei Loslager (Dreieck mit waagrechtem Strich).

Systeme starrer Körper bestehen aus mehreren starren Körpern, die miteinander verbunden sind. Die Verbindungen können ebenfalls starr sein oder durch Gelenke drehbar oder verschieblich sein. Berechnet werden diese Systeme, indem der Gesamtkörper geschnitten wird. Das Gesamtsystem zerfällt dann in mehrere Teilsysteme, wobei an den Schnittstellen die entsprechenden Kräfte und Momente angetragen werden.

Ideale Fachwerke sind Konstruktionen, die nur aus Stäben bestehen, die an den Verbindungsstellen (Knoten) gelenkig gelagert sind. Sie sind auf bestimmte Art und Weise miteinander verbunden, sodass die Knoten jeweils ein zentrales Kraftsystem bilden, also in den Stäben nur Zug- oder Druckkräfte übertragen werden, aber keine Querkräfte oder Momente, weshalb ideale Fachwerke besonders einfach zu berechnen sind. Ähnliche Bedeutung haben Gerberträger als Brückenkonstruktion. Sie lassen sich relativ einfach herstellen und reagieren unempfindlich gegenüber Auflagersetzungen. In Gerberträgern werden die Lasten hauptsächlich durch Biegemomente und Querkräfte abgetragen.[39]

Schnittgrößen

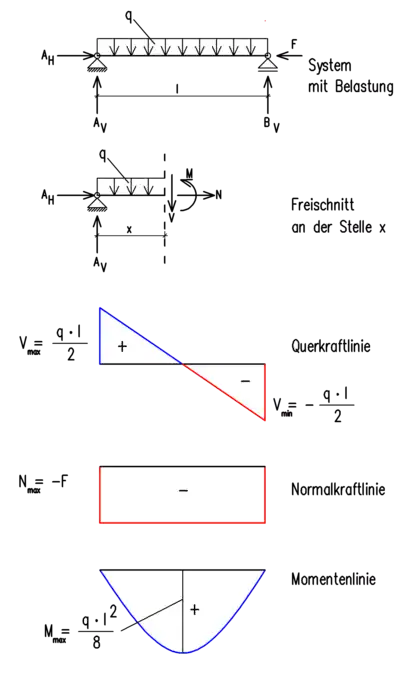
Schnittgrößen an einem Einfeldträger mit Streckenlast q und Längskraft F, Querkraft V, Normalkraft N und Biegemoment M. Die Querkraft ist an den Rändern am größten und hat einen linearen Verlauf. Der Momentenverlauf folgt hier einer quadratischen Funktion und hat sein Maximum in der Mitte.

Schnittgrößen sind Kräfte und Momente, die im Inneren von Körpern wirken. Sie können berechnet werden, indem die Körper in Gedanken durchgeschnitten werden. Von Interesse ist nicht die Schnittkraft an einer bestimmten Stelle, sondern der Verlauf der Schnittkräfte oder -momente über die Länge eines Stabes. Die Schnittgrößen werden zur Auslegung der Abmessungen der Bauteile oder Bauwerke benötigt (Bemessung oder Dimensionierung). Dazu muss jedoch die Festigkeit des Werkstoffes bekannt sein.

Bei einem stabförmigen Körper in der Ebene existieren in der Theorie I. Ordnung drei Arten von Schnittgrößen:

Die Querkraft, die senkrecht zur Balkenachse steht.
Die Normalkraft, die senkrecht (normal) zur Schnittfläche wirkt, also in Richtung der Stabachse.
Das Biegemoment, das den Balken zu biegen versucht.

Bei Stäben, die im dreidimensionalen Raum modelliert werden, gibt es insgesamt sechs Schnittgrößen, pro Dimension eine Kraft und ein Moment. Gegenüber dem ebenen System kommen für Stäbe je ein weiteres Biegemoment und eine Querkraft hinzu sowie das Torsionsmoment, das einen Stab zu verwinden (tordieren) versucht.[40] Bei „komplexeren“ Strukturen wie zum Beispiel einem Würfel kann man keine Schnittkräfte wie Normalkraft, Querkraft, Biegemoment und Torsionsmoment definieren, sondern nur ein Spannungstensor-Feld.

Schwerpunkt

Schwerpunkte werden benötigt, um die Wirkungslinien oder Angriffspunkte von verteilten Lasten zu berechnen. Dazu zählt die Gewichtskraft. Es wird unterschieden zwischen den rein geometrischen Schwerpunkten wie dem Strecken-, Flächen- oder Volumenschwerpunkt sowie dem Massenschwerpunkt.[41]

Grenzen der Statik und weiterführende Gebiete

Das Gebiet der Starrkörperstatik unterliegt definitionsgemäß zwei Einschränkungen: Zum einen werden nur starre Körper behandelt, zum anderen nur Körper, die sich im Gleichgewicht befinden, wodurch die Mathematik, die zur Beschreibung statischer Systeme nötig ist, vergleichsweise einfach wird. Mit Methoden der Starrkörperstatik nicht berechenbar sind dagegen Verformungen der Bauteile und Tragwerke sowie Kräfte in statisch unbestimmten Systemen.

Wenn nur die Einschränkung auf starre Körper aufgehoben wird, führt dies zu den Gebieten der Festigkeitslehre und der Baustatik. Lässt man stattdessen beschleunigte Bewegungen zu, so führt dies zur (Starrkörper-)Dynamik. Sowohl die Festigkeitslehre als auch die Dynamik sind fester Bestandteil der Technischen Mechanik, wie sie in vielen ingenieurwissenschaftlichen Studiengängen vorkommt, die Baustatik nur im Bauingenieurwesen. Die Mathematik, die für diese Gebiete nötig ist, befindet sich auf einem höheren Niveau.[42] So spielen beispielsweise Tensoren und Ableitungen eine große Rolle.

Festigkeitslehre

In der Festigkeitslehre werden deformierbare – nicht starre – Körper behandelt. Die auf die Körper wirkenden Kräfte führen dann zu Verformungen. Die Festigkeit ist ein Materialkennwert, der angibt, wie groß die auf die Querschnittsfläche bezogene Kraft (mechanische Spannung) sein darf, damit kein Versagen (Brechen, zu große Verformung) eintritt. Da Verformungen über Materialkennwerte mit den Kräften verbunden sind, lassen sich mit der Festigkeitslehre auch statisch unbestimmte Systeme berechnen.[43]

Baustatik

Die Baustatik ist ein Gebiet des Bauingenieurwesens. Wie auch die Festigkeitslehre nutzt sie Größen wie die mechanische Spannung, Verformung und Festigkeit. Ein besonderer Schwerpunkt liegt auf den verschiedenen Tragwerken wie z. B. Fachwerken, Einfeldträgern, Scheibenverbindungen und Stabwerken. Sie behandelt sowohl statisch bestimmte als auch unbestimmte Systeme.[44] Sie beinhaltet auch das Gleichgewicht in der verformten Lage, das realitätsnah ist, da (belastete) Systeme nur in der verformten Lage im Gleichgewicht sind.

Dynamik

Die Dynamik ist ein Gebiet, das in der Technischen Mechanik beschleunigte Bewegungen behandelt. Mit bekannten Kräften und Massen können die Beschleunigungen berechnet werden. Beschleunigte Körper befinden sich nicht im (statischen) Gleichgewicht. Wenn zusätzlich zu den wirkenden Kräften noch die sogenannten D’Alembert’schen Trägheitskräfte berücksichtigt werden, so befinden sich diese im dynamischen Gleichgewicht.

Geschichte

Bis ins frühe 18. Jahrhundert beherrschten das Hebelgesetz des Archimedes und das Kräfteparallelogramm die Entwicklung der Statik. Von Jordanus Nemorarius stammt die erste korrekte Beschreibung der Statik von Gewichten auf einer schiefen Ebene um 1250. Bei seiner Beschreibung des Hebels verwendet er erstmals das Prinzip der virtuellen Arbeit.

In der Renaissance basierte die Entwicklung vor allem auf Beobachtung und Experiment zur Lösung von Konstruktionsproblemen an Maschinen und Bauwerken (z. B. Leonardo da Vincis Konstruktion einer Bogenbrücke ohne Verbindungselemente). Seine Gedankenexperimente und Galileos Arbeiten zur Festigkeitslehre führten zur Abtrennung der Elastostatik von der Starrkörperstatik.[45] Galileo präzisierte auch die Archimedische Vorstellung von der Kraft und benutzte den Ausdruck des Moments für beliebig gerichtete Kräfte.

Seit dem späten 16. Jahrhundert wurde die Statik nicht mehr von Architekten und anderen Praktikern, sondern von Mathematikern und Physikern weiterentwickelt. Simon Stevin nutzte bereits vor 1600 das Kräfteparallelogramm und die virtuelle Verschiebung zur Auflösung von Kräften. Gilles Personne de Roberval baute 1669 eine Waage mit einem stets im Gleichgewicht befindlichen Parallelogramm-Gestänge. Pierre de Varignon führte zu Beginn des 18. Jahrhunderts Hebelgesetz, Kräfteparallelogramm und das von Bernoulli formulierte Prinzip der „virtuellen Geschwindigkeit“[46] auf die Gleichgewichtsbedingungen zurück, die sich auch aus dem Newtonschen System ableiten lassen, was Leonhard Euler 1775 zeigte. Die kinematische und die geometrische Richtung der Statik wurden 1788 von Joseph-Louis Lagrange in einer Synthese im Prinzip der virtuellen Verschiebungen zusammengefasst. Louis Poinsot gelang mit seiner Theorie der Kräftepaare 1803 ein weiterer Fortschritt in der Formulierung der Statik starrer Körper.[47]

Weblinks

Commons: Statik – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Stereostatik – Lern- und Lehrmaterialien

Literatur

Bruno Assmann: Technische Mechanik 1 – Statik. 19. Auflage. Oldenbourg, München 2010, ISBN 978-3-486-59133-0.
Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, Berlin/ Heidelberg 2011, ISBN 978-3-642-13805-8.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, Berlin/ Heidelberg 2012, ISBN 978-3-642-21711-1.
Martin Mayr: Technische Mechanik: Statik, Kinematik, Kinetik, Schwingungen, Festigkeitslehre,. 6., überarbeitete Auflage. Hanser, München/ Wien 2008, ISBN 978-3-446-41690-1.
Hans Albert Richard, Manuela Sander: Technische Mechanik – Statik. 5. Auflage. Springer-Vieweg, Wiesbaden 2016, ISBN 978-3-658-14906-2.
Mahir Sayir, Jürg Dual, Stephan Kaufmann, Edoardo Mazza: Ingenieurmechanik 1 – Statik. 3., überarbeitete Auflage. Springer-Vieweg, Wiesbaden 2015, ISBN 978-3-658-10046-9.
Christian Spura: Technische Mechanik 1 – Stereostatik. Springer-Vieweg, Wiesbaden 2016, ISBN 978-3-658-14985-7.

Hochschulschriften

Helmut Weyhmann: Entwicklung und methodischer Einsatz praxisorientierter Anschauungs- und Motivationshilfen für den Studiengang Maschinenbau an den Universitäten, Hoch- und Fachschulen zum Lehrabschnitt „Statik starrer Körper“. Dissertation. TU Dresden, 1992. DNB 930936442.

Einzelnachweise

Dankert Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 1.
Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014, S. 13.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 6.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. V.
Spura: Technische Mechanik 1 – Stereostatik. Springer, 2016, S. 3.
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016, S. 1.
Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014, S. 13.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 3.
Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015, S. 12.
Spura: Technische Mechanik 1 – Stereostatik. Springer, 2016, S. 3.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 3.
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016, S. 1.
Karsten Kirchgessner, Marco Schreck: Lern- und Übungsbuch zur Theoretischen Physik 1 – Klassische Mechanik. Oldenbourg, 2014, S. V (Vorwort).
Joseph Honerkamp, Hartmann Römer: Klassische, theoretische Physik. 4. Auflage. Springer, 2012, S. 52.
Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 1.
Böge, Böge: Technische Mechanik. 31. Auflage. Springer, 2015.
Dankert, Dankert: Technische Mechanik. 7. Auflage. Springer, 2013.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011.
Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012 (in der zweiten Auflage explizit als „Starrkörperstatik“ bezeichnet).
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016.
Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 1.
Böge, Böge: Technische Mechanik. 31. Auflage. Springer, 2015.
Dankert, Dankert: Technische Mechanik. 7. Auflage. Springer, 2013.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011.
Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012 (in der zweiten Auflage explizit als „Starrkörperstatik“ bezeichnet).
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016.
Fischer Günter: Technische Mechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig/Stuttgart 1994, S. 18: „Die Statik ist die Lehre vom Gleichgewicht der Kräfte am ruhenden starren Körper.“
Horst Herr: Technische Mechanik. Europa-Lehrmittel, 9. Auflage, 2008, S. 2: „In der Statik werden die durch Kräfte hervorgerufenen Verformungen nicht berücksichtigt.“
Bruno Assmann: Technische Mechanik – Statik. Oldenbourg, 15. Auflage, 1999, S. 13: „Da eine Verwechslung […] nicht möglich ist, spricht man einfach von Statik. In diesem Sinne ist die Statik die Lehre von der Wirkung von Kräften auf starre Körper im Gleichgewicht.“ (Kursivsetzung wie im Original).
Werner Skolaut (Hrsg.): Maschinenbau – Ein Lehrbuch für das ganze Bachelor-Studium. Springer, 2014, S. 20.
Dankert Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 1.
Dankert Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 167.
Bruno Assmann, Peter Selke: Technische Mechanik 2 – Festigkeitslehre. 18. Auflage. Springer, Oldenbourg, S. IX (Vorwort).
Balke: Einführung in die Technische Mechanik – Festigkeitslehre. 3. Auflage. Springer, 2014, S. V (Vorwort zur ersten Auflage), S. 1.
Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 1.
Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 2, 195 u. 197, doi:10.1007/978-3-658-09155-2 (online).
Dreyer u. a.: Technische Mechanik – Kinematik und Kinetik. 11. Auflage. Springer, 2012, 69 f.
Dubbel: Handbuch Maschinenbau. 24. Auflage. S. C30.
Assmann, Selke: Technische Mechanik 2 – Festigkeitslehre. 18. Auflage. 2013, S. 1 f., 355.
Balke: Einführung in die Technische Mechanik – Festigkeitslehre. 3. Auflage. Springer, 2014, S. 1 f., 20, 23.
Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 173.
Fischer Günter: Technische Mechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig/ Stuttgart 1994, S. 137.
Kurt Beyer: Die Statik im Stahlbetonbau. Ein Lehr- und Handbuch der Baustatik. Zweite, vollständig neubearbeitete Auflage. Springer-Verlag, Berlin/ Göttingen/ Heidelberg 1956, ISBN 978-3-642-92665-5 (eingeschränkte Vorschau in der Google-Buchsuche).
Kurt Hirschfeld: Baustatik Theorie und Beispiele. 5., unveränderte Auflage. Springer, Berlin/ Heidelberg/ New York 2006, ISBN 3-540-36772-1, Erster Teil – Berechnung statisch unbestimmter Systeme, S. 236–768 (online).
Walther Kaufmann: Statik der Tragwerke. Hrsg.: Ferdinand Schleicher (= Handbibliothek für Bauingenieure. Ein Hand- und Nachschlagebuch für Studium und Praxis). Vierte ergänzte und verbesserte Auflage. Springer-Verlag, Berlin/Heidelberg 1957, ISBN 978-3-540-02154-4, doi:10.1007/978-3-662-13040-7 (eingeschränkte Vorschau in der Google-Buchsuche).
Fritz Stüssi: Statisch unbestimmte Systeme (= Vorlesungen über Baustatik. Band 2). Zweite Auflage. Springer-Verlag, Basel 1971, ISBN 3-0348-5947-3, doi:10.1007/978-3-0348-5946-2 (eingeschränkte Vorschau in der Google-Buchsuche).
Konstantin Meskouris, Erwin Hake: Statik der Stabtragwerke: Einführung in die Tragwerkslehre. 2. Auflage. Springer, 2009, ISBN 978-3-540-88993-9, ISSN 0937-7433, Insbesondere: Kapitel 8. Das Kraftgrößenverfahren zur Berechnung statisch unbestimmter Stabwerke und Kapitel 9. Das Drehwinkelverfahren, doi:10.1007/978-3-540-88993-9 (online).
Bernhard Pichler, Josef Eberhardsteiner: Baustatik VO – LVA-Nr 202.065. Hrsg.: E202 Institut für Mechanik der Werkstoffe und Strukturen – Fakultät Bauingenieurwesen, TU Wien. SS 2017 Auflage. TU Verlag, Wien 2017, ISBN 978-3-903024-41-0, V. Statisch unbestimmte Stabtragwerke, 15.2. Kraftgrößenverfahen, 15.3. Dreimomentengleichung, 19. Drehwinkelverfahren, 22. Einführung in die schubstarre Fließgelenktheorie I. Ordnung, 23. Reziprozitätstheoreme als Grundlage für die Einflusslinien (Erstausgabe: 2012).
Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 1 f., doi:10.1007/978-3-658-09155-2 (online).
Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, (Kraft) S. 1 ff., (Moment) S. 19 ff.
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016, (Kraft) S. 5 ff., (Moment) S. 33 ff.
Gross u. a.: Statik. 11. Auflage. 2011, S. 7, 49, 54.
Sayir: Statik. 3. Auflage, S. 67, 87.
Mahnken: Statik. 2012, S. 13, 97 f.
Jürgen Dankert, Helga Dankert: Technische Mechanik – Statik, Festigkeitslehre, Kinematik/Kinetik. 7. Auflage. Springer, 2013, S. 3.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 37.
Jürgen Dankert, Helga Dankert: Technische Mechanik – Statik, Festigkeitslehre, Kinematik/Kinetik. 7. Auflage. Springer, 2013, S. 4.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 38.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 40.
Bruno Assmann: Technische Mechanik 1 – Statik. Oldenbourg, 15. Auflage, 1999, S. 20.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 39.
Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 3, doi:10.1007/978-3-658-09155-2 (online).
Jürgen Dankert, Helga Dankert: Technische Mechanik – Statik, Festigkeitslehre, Kinematik/Kinetik. 7. Auflage. Springer, 2013, S. 3.
Bruno Assmann: Technische Mechanik 1 – Statik. 15. Auflage. Oldenbourg, 1999, S. 22.
Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 9 f.
Bruno Assmann: Statik. 15. Auflage, S. 14.
Böge: Technische Mechanik. 31. Auflage, S. 3.
Dankert: Technische Mechanik. 7. Auflage, S. 2.
Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014, S. 13.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 7 f.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 15.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 11.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 22.
Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 8–14.
Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 4 f., doi:10.1007/978-3-658-09155-2 (online).
Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 10 f.
Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 6, doi:10.1007/978-3-658-09155-2 (online).
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 27–33.
Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 5–8.
Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 21–24, doi:10.1007/978-3-658-09155-2 (online).
Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 9, doi:10.1007/978-3-658-09155-2 (online).
Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 48 f.
Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 62 f. u, S. 80.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 332 f.
Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 183.
Gross, Hauger, Schröder, Wall: Technische Mechanik 3 – Statik. 13. Auflage. Springer, 2015, S. V (Vorwort).
Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015, S. 154.
Dieter Dinkler: Grundlagen der Baustatik. 4. Auflage. Springer, 2016, S. VI.
Massimo Corradi: The Mechanical Sciences in Antiquity. Edizioni di Storia, Genua 2008.
Virtuelle Geschwindigkeit. In: Pierer’s Universal-Lexikon. Band 18, Altenburg 1864, S. 614 (online).
Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin 2018, ISBN 978-3-433-03229-9, S. 31f.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Dankert Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 1.
Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014, S. 13.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 6.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. V.
Spura: Technische Mechanik 1 – Stereostatik. Springer, 2016, S. 3.
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016, S. 1.

[2] Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014, S. 13.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 3.
Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015, S. 12.
Spura: Technische Mechanik 1 – Stereostatik. Springer, 2016, S. 3.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 3.
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016, S. 1.

[3] Karsten Kirchgessner, Marco Schreck: Lern- und Übungsbuch zur Theoretischen Physik 1 – Klassische Mechanik. Oldenbourg, 2014, S. V (Vorwort).

[4] Joseph Honerkamp, Hartmann Römer: Klassische, theoretische Physik. 4. Auflage. Springer, 2012, S. 52.

[5] Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 1.
Böge, Böge: Technische Mechanik. 31. Auflage. Springer, 2015.
Dankert, Dankert: Technische Mechanik. 7. Auflage. Springer, 2013.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011.
Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012 (in der zweiten Auflage explizit als „Starrkörperstatik“ bezeichnet).
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016.

[6] Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 1.
Böge, Böge: Technische Mechanik. 31. Auflage. Springer, 2015.
Dankert, Dankert: Technische Mechanik. 7. Auflage. Springer, 2013.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011.
Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012 (in der zweiten Auflage explizit als „Starrkörperstatik“ bezeichnet).
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016.
Fischer Günter: Technische Mechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig/Stuttgart 1994, S. 18: „Die Statik ist die Lehre vom Gleichgewicht der Kräfte am ruhenden starren Körper.“
Horst Herr: Technische Mechanik. Europa-Lehrmittel, 9. Auflage, 2008, S. 2: „In der Statik werden die durch Kräfte hervorgerufenen Verformungen nicht berücksichtigt.“
Bruno Assmann: Technische Mechanik – Statik. Oldenbourg, 15. Auflage, 1999, S. 13: „Da eine Verwechslung […] nicht möglich ist, spricht man einfach von Statik. In diesem Sinne ist die Statik die Lehre von der Wirkung von Kräften auf starre Körper im Gleichgewicht.“ (Kursivsetzung wie im Original).

[7] Werner Skolaut (Hrsg.): Maschinenbau – Ein Lehrbuch für das ganze Bachelor-Studium. Springer, 2014, S. 20.

[8] Dankert Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 1.

[9] Dankert Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 167.
Bruno Assmann, Peter Selke: Technische Mechanik 2 – Festigkeitslehre. 18. Auflage. Springer, Oldenbourg, S. IX (Vorwort).
Balke: Einführung in die Technische Mechanik – Festigkeitslehre. 3. Auflage. Springer, 2014, S. V (Vorwort zur ersten Auflage), S. 1.
Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 1.

[10] Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 2, 195 u. 197, doi:10.1007/978-3-658-09155-2 (online).

[11] Dreyer u. a.: Technische Mechanik – Kinematik und Kinetik. 11. Auflage. Springer, 2012, 69 f.

[12] Dubbel: Handbuch Maschinenbau. 24. Auflage. S. C30.
Assmann, Selke: Technische Mechanik 2 – Festigkeitslehre. 18. Auflage. 2013, S. 1 f., 355.
Balke: Einführung in die Technische Mechanik – Festigkeitslehre. 3. Auflage. Springer, 2014, S. 1 f., 20, 23.
Holzmann, Meyer, Schumpich: Technische Mechanik – Festigkeitslehre. 10. Auflage. Springer, S. vii (Vorwort zur 9. Auflage), S. 173.
Fischer Günter: Technische Mechanik. Deutscher Verlag für Grundstoffindustrie, Leipzig/ Stuttgart 1994, S. 137.

[13] Kurt Beyer: Die Statik im Stahlbetonbau. Ein Lehr- und Handbuch der Baustatik. Zweite, vollständig neubearbeitete Auflage. Springer-Verlag, Berlin/ Göttingen/ Heidelberg 1956, ISBN 978-3-642-92665-5 (eingeschränkte Vorschau in der Google-Buchsuche).
Kurt Hirschfeld: Baustatik Theorie und Beispiele. 5., unveränderte Auflage. Springer, Berlin/ Heidelberg/ New York 2006, ISBN 3-540-36772-1, Erster Teil – Berechnung statisch unbestimmter Systeme, S. 236–768 (online).
Walther Kaufmann: Statik der Tragwerke. Hrsg.: Ferdinand Schleicher (= Handbibliothek für Bauingenieure. Ein Hand- und Nachschlagebuch für Studium und Praxis). Vierte ergänzte und verbesserte Auflage. Springer-Verlag, Berlin/Heidelberg 1957, ISBN 978-3-540-02154-4, doi:10.1007/978-3-662-13040-7 (eingeschränkte Vorschau in der Google-Buchsuche).
Fritz Stüssi: Statisch unbestimmte Systeme (= Vorlesungen über Baustatik. Band 2). Zweite Auflage. Springer-Verlag, Basel 1971, ISBN 3-0348-5947-3, doi:10.1007/978-3-0348-5946-2 (eingeschränkte Vorschau in der Google-Buchsuche).
Konstantin Meskouris, Erwin Hake: Statik der Stabtragwerke: Einführung in die Tragwerkslehre. 2. Auflage. Springer, 2009, ISBN 978-3-540-88993-9, ISSN 0937-7433, Insbesondere: Kapitel 8. Das Kraftgrößenverfahren zur Berechnung statisch unbestimmter Stabwerke und Kapitel 9. Das Drehwinkelverfahren, doi:10.1007/978-3-540-88993-9 (online).
Bernhard Pichler, Josef Eberhardsteiner: Baustatik VO – LVA-Nr 202.065. Hrsg.: E202 Institut für Mechanik der Werkstoffe und Strukturen – Fakultät Bauingenieurwesen, TU Wien. SS 2017 Auflage. TU Verlag, Wien 2017, ISBN 978-3-903024-41-0, V. Statisch unbestimmte Stabtragwerke, 15.2. Kraftgrößenverfahen, 15.3. Dreimomentengleichung, 19. Drehwinkelverfahren, 22. Einführung in die schubstarre Fließgelenktheorie I. Ordnung, 23. Reziprozitätstheoreme als Grundlage für die Einflusslinien (Erstausgabe: 2012).

[14] Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 1 f., doi:10.1007/978-3-658-09155-2 (online).

[15] Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, (Kraft) S. 1 ff., (Moment) S. 19 ff.
Richard, Sander: Technische Mechanik – Statik. 5. Auflage. Springer, 2016, (Kraft) S. 5 ff., (Moment) S. 33 ff.
Gross u. a.: Statik. 11. Auflage. 2011, S. 7, 49, 54.
Sayir: Statik. 3. Auflage, S. 67, 87.
Mahnken: Statik. 2012, S. 13, 97 f.

[16] Jürgen Dankert, Helga Dankert: Technische Mechanik – Statik, Festigkeitslehre, Kinematik/Kinetik. 7. Auflage. Springer, 2013, S. 3.

[17] Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 37.

[18] Jürgen Dankert, Helga Dankert: Technische Mechanik – Statik, Festigkeitslehre, Kinematik/Kinetik. 7. Auflage. Springer, 2013, S. 4.

[19] Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 38.

[20] Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 40.

[21] Bruno Assmann: Technische Mechanik 1 – Statik. Oldenbourg, 15. Auflage, 1999, S. 20.

[22] Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 39.

[23] Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 3, doi:10.1007/978-3-658-09155-2 (online).

[24] Jürgen Dankert, Helga Dankert: Technische Mechanik – Statik, Festigkeitslehre, Kinematik/Kinetik. 7. Auflage. Springer, 2013, S. 3.

[25] Bruno Assmann: Technische Mechanik 1 – Statik. 15. Auflage. Oldenbourg, 1999, S. 22.

[26] Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 9 f.

[27] Bruno Assmann: Statik. 15. Auflage, S. 14.
Böge: Technische Mechanik. 31. Auflage, S. 3.
Dankert: Technische Mechanik. 7. Auflage, S. 2.
Wittenburg u. a. (Hrsg.): Das Ingenieurwissen – Technische Mechanik. Springer, 2014, S. 13.
Gross, Hauger, Schröder, Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 7 f.
Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 15.

[28] Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 11.

[29] Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 22.

[30] Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 8–14.

[31] Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 4 f., doi:10.1007/978-3-658-09155-2 (online).

[32] Dietmar Gross, Werner Hauger, Jörg Schröder, Wolfgang Wall: Technische Mechanik 1 – Statik. 11. Auflage. Springer, 2011, S. 10 f.

[33] Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 6, doi:10.1007/978-3-658-09155-2 (online).

[Mahnken-34] Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 27–33.

[35] Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 5–8.

[36] Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 21–24, doi:10.1007/978-3-658-09155-2 (online).

[37] Alfred Böge, Wolfgang Böge: Technische Mechanik – Statik – Reibung – Dynamik – Festigkeitslehre – Fluidmechanik. 31. Auflage. Springer, 2015, ISBN 978-3-658-09154-5, S. 9, doi:10.1007/978-3-658-09155-2 (online).

[38] Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 48 f.

[39] Jürgen Dankert, Helga Dankert: Technische Mechanik. 7. Auflage. Springer, 2013, S. 62 f. u, S. 80.

[40] Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 332 f.

[41] Rolf Mahnken: Lehrbuch der Technischen Mechanik – Statik. Springer, 2012, S. 183.

[42] Gross, Hauger, Schröder, Wall: Technische Mechanik 3 – Statik. 13. Auflage. Springer, 2015, S. V (Vorwort).

[43] Sayir, Dual, Kaufmann, Mazza: Ingenieurmechanik 1 – Grundlagen und Statik. 3. Auflage. Springer, 2015, S. 154.

[44] Dieter Dinkler: Grundlagen der Baustatik. 4. Auflage. Springer, 2016, S. VI.

[45] Massimo Corradi: The Mechanical Sciences in Antiquity. Edizioni di Storia, Genua 2008.

[46] Virtuelle Geschwindigkeit. In: Pierer’s Universal-Lexikon. Band 18, Altenburg 1864, S. 614 (online).

[47] Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin 2018, ISBN 978-3-433-03229-9, S. 31f.