Simon Stevin

Simon Stevin (latinisiert Simon Stevinus; * 1548/49 in Brügge (Flandern); † 1620) war ein flämischer Mathematiker, Physiker und Ingenieur. Er war auf vielen Gebieten der Wissenschaften theoretisch und praktisch tätig, aber am bekanntesten ist er für seine Übersetzungen vieler mathematischer Begriffe in die niederländische Sprache. Er schlug außerdem bereits 1585 ein rein dezimales Maßsystem vor.

Simon Stevin

Lebenslauf

Oeuvres mathematiques, 1634

Von Stevins Lebensumständen ist sehr wenig bekannt; der genaue Tag seiner Geburt und der Tag (im Frühling) und der Ort seines Todes (Den Haag oder Leiden) sind gleichermaßen unbekannt.[1] Er war der illegitime Sohn von Antheunis Stevin und Cathelijen van de Poort, wohlhabende Bürger aus Brügge. Ein paar Hinweise in seinem Werk besagen, dass er als kaufmännischer Angestellter (Buchhalter) in Brügge und Antwerpen begann, dass er zwischen 1571 und 1577 nach Polen, Dänemark, Norwegen und andere Länder Nordeuropas reiste, und dass er ab 1581 in Leiden war, wo er ab 1583 an der Universität studierte. Über seinen religiösen Hintergrund und ob er vor Verfolgung in den spanischen Niederlanden dorthin floh ist nicht bekannt. Er war mit Prinz Moritz von Oranien bekannt, der seinen Rat bei vielen Gelegenheiten suchte und ihn zu einem Angestellten und Direktor des sogenannten Waterstaat machte (der Regierungsbehörde für Wasserangelegenheiten) und später (ab 1604) zum General-Quartiermeister der Armee. Er war auch Verwalter der Güter von Moritz von Oranien, arbeitete für diesen als Ingenieur und eröffnete für diesen eine Ingenieursschule in Leiden.

1610 heiratete er Catherine Cray, mit der er vier Kinder hatte. Der Sohn Hendrick war ebenfalls ein begabter Wissenschaftler und veröffentlichte einige von Stevins Manuskripten.

In Brügge gibt es einen Simon-Stevin-Platz mit einer Statue von ihm, die 1846 von Eugène Simonis geschaffen wurde.

Der Mondkrater Stevinus und der Asteroid (2831) Stevin sind nach ihm benannt.

Wissenschaftliche Leistungen

Entdeckungen und Erfindungen: der Segelwagen, Windmühlen

Segelwagen von Stevin für Prinz Moritz von Oranien

Seine Verdienste sind vielfältig. Seine Zeitgenossen waren besonders beeindruckt von seiner Erfindung eines Fahrzeugs mit Segeln, von dem ein kleines Modell in Scheveningen bis 1802 aufbewahrt wurde. Das Fahrzeug war lange zuvor verloren gegangen, aber man weiß, dass Stevin es ungefähr im Jahr 1600 mit Prinz Moritz von Oranien und 26 anderen an der Küste von Scheveningen und Petten benutzte, dass es allein vom Wind angetrieben wurde und dass es eine Geschwindigkeit erreichte, welche die von Pferden überstieg.

Stevin verbesserte auch die zur Entwässerung des Landes eingesetzten Windmühlen[2] und es existieren von Stevin eine Reihe von Patenten, die ihn wohlhabend machten. Er schrieb auch eine Abhandlung über Windmühlen.

Philosophie der Wissenschaften

Eine andere Idee von Stevin, für die ihm Hugo Grotius große Zustimmung erteilte, war seine Theorie eines vergangenen Zeitalters der Weisheit. Das anzustrebende Ziel ist die Hervorbringung eines zweiten Zeitalters der Weisheit, in dem die Menschheit alle ihre früheren Kenntnisse wiederentdeckt. - Seine Landsleute waren stolz darauf, dass er in ihrem eigenen Dialekt schrieb, den er für eine universelle Sprache geeignet hielt, weil keine andere über so viele einsilbige Wortstämme verfügt.

Geometrie und Physik

Stevin war der erste, der gezeigt hat, wie man regelmäßige und unregelmäßige Vielflächenkörper modellieren kann, indem man sie in der Ebene skizziert. Stevin unterschied auch das stabile vom instabilen Gleichgewicht. Er bewies mit dem Stevinschen Gedankenexperiment das Gesetz vom Gleichgewicht auf einer schiefen Ebene.

Statue von Stevin von Eugène Simonis auf dem Stevinplatz in Brügge

Er zeigte vor Pierre de Varignon die Auflösung von Kräften, was vorher noch nicht erkannt worden war, obwohl es eigentlich eine einfache Folge des Gesetzes ihrer Zusammensetzung ist (Kräfteparallelogramm und Virtuelle Verschiebung).

Stevin entdeckte das hydrostatische Paradoxon, nach dem der Druck am Boden einer Flüssigkeit unabhängig von der Form des Behälters ist und nur von der Wasserstandshöhe über dem Boden abhängt.

Er gab auch das Maß des Druckes auf eine beliebige Stelle der Wand eines Behälters an und erklärte, weshalb Flüssigkeiten in kommunizierenden Röhren einen gleichmäßigen Wasserstand haben.

Stevin war ein unbedingter Befürworter des Kopernikanischen Systems, das er auch in seinem Buch De Hemelloop darstellte. 1590 stellte er die Theorie auf, dass die Gezeiten durch die Anziehung des Mondes zu erklären sind.

1586 demonstrierte er, dass zwei Objekte mit verschiedenem Gewicht mit derselben Geschwindigkeit zu Boden fallen, was üblicherweise als Erkenntnis von Galileo Galilei gilt, aber auch schon von Physikern vor Galilei erkannt wurde (im Fall von Stevin kam der Einfluss indirekt über Giovanni Battista Benedetti).

Auch legte er überzeugend dar, dass ein Perpetuum Mobile nicht existieren kann.

Festungen

Stevin stand seit ungefähr 1593 in den Diensten des Prinzen Moritz von Oranien. 1599 erhielt Stevin den Auftrag, eine „instructie“ zur Gründung einer Ingenieurschule zu entwerfen, die mit der Universität Leiden verbunden sein sollte und die dann auch eröffnet wurde.[3] Dafür schrieb er auch 1594 ein Lehrbuch (Stercktenbouwinge), das allgemein von den holländischen Festungsingenieuren benutzt wurde. Sein Eintreten für die Lehre der Wissenschaft der Festungen an Universitäten und die Existenz solcher Vorlesungen in Leiden haben zu dem Eindruck geführt, dass er selbst diesen Lehrstuhl ausfüllte, aber dies ist ein Irrglaube, denn Stevin hatte niemals direkte Beziehungen mit der Universität, obwohl er in Leiden wohnte. Er war häufig Berater bei Befestigungen als unter Moritz von Oranien ein ganzer Ring von Festungen in den Niederlanden angelegt wurde, die eigentliche Ingenieursarbeit führten aber andere aus (wie Adriaan Anthonisz, David van Orliens, Johan van Rijswijck, Johan van Valckenburgh, Samuel Marolois).

Stevin war anscheinend der erste, der es zum Axiom gemacht hat, dass Festungen nur mit Artillerie zu verteidigen sind. Vorher hat die Verteidigung meistens auf kleine Feuerwaffen vertraut.

Er war der Erfinder der Verteidigung durch ein System von Schleusen, was sich für die Niederlande als von höchster Wichtigkeit erwies.

Buchhaltung

Die doppelte Buchführung könnte Stevin als kaufmännischer Angestellter in Antwerpen praktisch kennengelernt haben oder durch die Werke von italienischen Autoren wie Luca Pacioli und Gerolamo Cardano. Jedenfalls war er der erste, der die Anwendung von unpersönlichen Konten im nationalen Staatshaushalt empfahl. Er praktizierte das für Prinz Moritz und empfahl es dem französischen Staatsmann Sully.

Dezimalzahlen

Simon Stevins größter Erfolg war unbestritten ein kleines Lehrbuch mit dem Titel De Thiende („Das Zehntel“), das erstmals 1585 auf Holländisch veröffentlicht wurde.[4] De Thiende dürfte sich nach der Veröffentlichung einer großen Popularität erfreut haben,[5] bis 1650 gab es zwei niederländische, drei französische und zwei englische Versionen.[6]

Die Titelseite des Lehrbuches trägt die Beschriftung: „DE THIENDE welche lehrt, mit unerhörter Leichtigkeit alle Rechnungen, die unter den Menschen nötig werden, durch Zahlen ohne Brüche zu erledigen. Beschrieben von Simon Stevin aus Brügge. Zu Leyden bei Christoffel Plantijn. M. D. LXXXV.“[4] Das eigentliche Buch beginnt mit einer Vorrede, in welche Stevin „[d]en Astronomen, Landmessern, Tuchmessern, Weinmessern, Stereometern im allgemeinen, Münzmeistern und allen Kaufleuten […] Glück [wünscht].“[4] Der Hauptteil fasst eine Inhaltsangabe, welcher zu entnehmen ist, dass „De Thiende“ zweiteilig aufgebaut ist.[4] Der erste Teil erklärt die Idee hinter der neuen Zahlendarstellung, der zweite erläutert das Rechnen mit den neuartigen Zahlen anhand der vier Grundrechenarten und zwei Anmerkungen. Letztgenannte beinhalten Hinweise auf den Umgang mit dem Fall, dass der Dividend beim Teilen kleiner als der Divisor ist und auf das Wurzelziehen.[4]

Dezimalbrüche waren ca. 500 Jahre vor seiner Zeit schon angewandt worden, um Quadratwurzeln zu ziehen, aber keiner vor Stevin führte sie zum täglichen Gebrauch ein. Und er war sich der Bedeutung seiner Neuerung so bewusst, dass er erklärte, dass die allgemeine Einführung von Dezimalmünzen, -Maßen und -Gewichten nur eine Frage der Zeit seien, womit er recht behielt.

Seine Schreibweise der Dezimalstellen ist aber sehr unhandlich. Der Punkt, der die Ganzzahlen von den Zehnerbrüchen trennt, scheint eine Erfindung von Bartholomäus Pitiscus zu sein, in dessen trigonometrischen Tafeln er 1612 auftauchte. Der Punkt wurde auch von John Napier in seinen logarithmischen Papieren 1614 und 1619 akzeptiert.

Rahmen

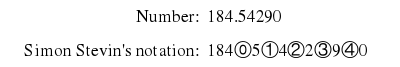
Stevin schrieb kleine Kreise um die Exponenten der verschiedenen Potenzen der Zehntel. Die Tatsache, dass Stevin diese eingekreisten Zahlen benutzte, um Exponenten darzustellen, ist offensichtlich, weil er dieselben Zeichen für die Potenzen von algebraischen Größen verwandte. Er vermied nicht einmal gebrochene Exponenten, und er kannte nur negative Exponenten nicht.

Stevin schrieb auch über andere wissenschaftlichen Themen: Optik, Geografie, Astronomie, und viele seiner Schriften wurden von W. Snellius (Willebrord Snell) in das Lateinische übersetzt. Es gibt zwei vollständige französische Ausgaben seiner Werke, beide in Leiden gedruckt, eine von 1608 und die andere von 1634.

Musiktheorie

In seiner Schrift Van de Spiegheling der Singconst formulierte Stevin eine polemische Antithese gegen Euklids Tonsystemtheorie, der die Unteilbarkeit vieler musikalischer Intervalle wie Oktave, Quinte, Quarte und Ganzton aufgrund ihrer Irrationalität behauptete. Stevin erklärte das Irrationale für rational, weil er in der Lage war, mit seinen Dezimalzahlen auch die Wurzeln der Proportionen besagter Intervalle zu definieren. Er ging in seiner Tonsystemtheorie von beliebigen Wurzeln der Oktav-Proportion 2 aus und definierte die zwölfstufige Lautenstimmung über Potenzen der zwölften Wurzel aus 2, die er dann durch Dezimalbrüche gut näherte. Das entspricht einer Umrechnung der additiven Intervalle nach Aristoxenos in die multiplikativen Proportionen mit einer Exponentialfunktion zur Basis 2. Er verwarf die übliche Interpretation als temperiertes Tonsystem, weil er die pythagoreische Stimmung der Konsonanzen nicht als wahr ansah, sondern seine Wurzelwerte als wahre Werte betrachtete.

Wortschöpfungen (Neologismen)

Stevin hielt Niederländisch für eine ausgezeichnete Sprache für das wissenschaftliche Schreiben, und er übersetzte viele mathematische Ausdrücke ins Niederländische. Als Folge davon ist Niederländisch die einzige westeuropäische Sprache, die viele mathematische Ausdrücke enthält, die nicht vom Lateinischen (bzw. Griechischen) abstammen. So kam es zum Beispiel, dass „wiskunde“ im Niederländischen das Wort für Mathematik ist.

Er hatte ein Auge für die Wichtigkeit, dass die Sprache der Wissenschaft dieselbe ist wie die Sprache der Handwerker, und das zeigt sich in der Widmung seines Buches De Thiende („Das Zehntel“): 'Simon Stevin wünscht den Sternguckern, Vermessern, Teppichvermessern, Körpervermessern im Allgemeinen, Münzvermessern und Handelsleuten viel Glück.' Weiter unten in dem Buch schreibt er: „[dieser Text] lehrt uns alle Berechnungen, die das Volk braucht, ohne Brüche zu benutzen. Man kann alle Operationen reduzieren auf Addieren, Subtrahieren, Multiplizieren und Dividieren mit Ganzzahlen.“

Die Worte, die er erfand, entwickelten sich: 'aftrekken' (abziehen) und 'delen' (teilen) blieben gleich, aber im Laufe der Zeit wurde aus 'menigvuldigen' (multiplizieren) 'vermenigvuldigen' (das hinzugefügte 'ver' hat keine Bedeutung), und aus 'vergaderen' (addieren) wurde 'optellen'. Das Wort 'zomenigmaal' (wörtlich 'so viele Male') wurde im modernen Niederländisch zu dem wohl weniger poetischen Quotient.

Schriften

Titelseite Hypomnemata mathematica

Neben anderen Werken veröffentlichte er:

Tafelen van Interest (Zinstafeln) 1582
Problemata geometrica 1583
De Thiende (Das Zehntel) 1585 (hiermit wurden die Dezimalzahlen in Europa eingeführt)[4]
La pratique d’arithmétique 1585
L’arithmétique in 1585 (hier wurde eine allgemeine Behandlung algebraischer Gleichungen vorgestellt)
De Beghinselen der Weegconst 1586
De Beghinselen des Waterwichts (Prinzipien des Wassergewichts) 1586 (über das Thema Hydrostatik)
Vita Politica. Het Burgherlick leven (Das bürgerliche Leben) 1590
De Sterktenbouwing (Die Konstruktion von Festungen) 1594
De Havenvinding (Positionsfindung) 1599
De Hemelloop 1608 (Der Himmelslauf)
Wiskonstighe Ghedachtenissen (Mathematische Memoiren). Diese schließt frühere Werke ein wie De Driehouckhandel (Trigonometrie), De Meetdaet (Praxis der Vermessung), und De Deursichtighe (Perspektive)
- Lateinische Übersetzung mit dem Titel Hypomnemata mathematica durch Willebrord van Roijen Snell (Snellius)
Castrametatio, dat is legermeting and Nieuwe Maniere van Stercktebou door Spilsluysen (Neue Art Schleusen zu bauen) 1617
De Spiegheling der Singconst (Theorie der Kunst des Singens)
Œuvres mathématiques..., Leyde, 1634 (architectura.cesr.univ-tours.fr)
Charles van den Heuvel De Huysbou. A reconstruction of an unfinished treatise on architecture, town planning and civil engineering by Simon Stevin, History of Science and Scholarship in the Netherlands, Band 7, Königlich Niederländische Akademie der Wissenschaften 2007

Die Gesammelten Werke von Stevin wurden herausgegeben von Ernst Crone, E.J. Dijksterhuis, R.J. Forbes, M.G.J. Minnaert, A. Pannekoek: The Principal Works of Simon Stevin, Amsterdam: Swets & Zeitlinger, 1955–1966 (Band 1 Mechanik, Band 2a, 2b Mathematik, 3 Astronomie/Navigation, 4 Kriegskunst, 5 Ingenieurswesen – Musik – Ziviles Leben) Online

Literatur

Eduard Jan Dijksterhuis Simon Stevin, ’s-Gravenhage 1943 (niederländisch)
- gekürzte englische Ausgabe Simon Stevin. Science in the Netherlands around 1600, Den Haag, Martinus Nijhoff 1970
Marcel Minnaert: Stevin, Simon. In: Charles Coulston Gillispie (Hrsg.): Dictionary of Scientific Biography. Band 13: Hermann Staudinger – Giuseppe Veronese. Charles Scribner’s Sons, New York 1976, S. 47–51.
Dirk Struik The land of Stevin and Huygens. A sketch of science and technology in the dutch republic during the golden age, Reidel 1981 (Kapitel 5 zu Stevin)
K. van Berkel The legacy of Stevin. A chronological narrative, Leiden 1999
Jozef T. Devreese, Guido Vanden Berghe Magic is no magic. The wonderful world of Simon Stevin, WIT Press, Southampton (Boston), 2008
Rolf Grabow Simon Stevin, Teubner, Leipzig 1985
Bergmann, Schaefer – Lehrbuch der Experimentalphysik – Band I – Mechanik, Akustik, Wärme – 9. Auflage – Kapitel II, 61f
Fritz Krafft (Hrsg.): „Vorstoß ins Unbekannte“ – Lexikon großer Naturwissenschaftler; Wiley-VCH 1999, ISBN 3-527-29656-5, 395f
Moritz Cantor: Stevin, Simon. In: Allgemeine Deutsche Biographie (ADB). Band 36, Duncker & Humblot, Leipzig 1893, S. 158–160.
Henri Bosmans Simon Stevin, Biographie Nationale 1924, pdf
Flip G. Droste: Simon Stevin. Wetenschapper in oorlogstijd, 1548–1620. Aspekt, Soesterberg 2007, ISBN 978-90-5911-524-8.
Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium, Ernst & Sohn 2018, S. 29f und S. 1064 (Biografie), ISBN 978-3-433-03229-9.
Guido Vanden Berghe, Dieter Viaene, Ludo Vandamme: Simon Stevin van Brugghe (1548–1520). Hij veranderde de wereld. Sterck & Devreese, Gorredijk 2020, ISBN 978-90-5615-655-8.

Einzelnachweise

Minnaert, Dictionary of Scientific Biography, gibt als Sterbeort Den Haag, März 1620 an
Frederick Stokhuyzen The Dutch Windmill, Abschnitt Geschichte (Memento des Originals vom 5. Juli 2017 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.let.rug.nl
Jürgen Soenke: Johan van Rijswijck und Johan van Valckenburgh – Die Befestigung deutscher Städte und Residenzen 1600–1625 durch holländische Ingenieuroffiziere. Mitteilungen des Mindener Geschichtsvereins, Jahrgang 46 (1974), S. 9–39.
Helmuth Gericke, Kurt Vogel: De Thiende von Simon Stevin. Das erste Lehrbuch der Dezimalbruchrechnung nach der holländischen und der französischen Ausgabe von 1585. In: Ostwalds Klassiker der exakten Wissenschaften. Band 1. Akademische Verlagsgesellschaft Frankfurt, Frankfurt am Main 1965.
José Ferreirós: Mathematical Knowledge and the Interplay of Practices. Oxford 2016, S. 211.
Hensk J. M. Bos: Simon Stevin, mathématicien. In: Raphaël De Smedt (Hrsg.): Simon Stevin 1548–1620. L'émergence de la nouvelle science. Turnhout 2004, S. 51.

Weblinks

Commons: Simon Stevin – Sammlung von Bildern, Videos und Audiodateien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Minnaert, Dictionary of Scientific Biography, gibt als Sterbeort Den Haag, März 1620 an

[2] Frederick Stokhuyzen The Dutch Windmill, Abschnitt Geschichte (Memento des Originals vom 5. Juli 2017 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/www.let.rug.nl

[3] Jürgen Soenke: Johan van Rijswijck und Johan van Valckenburgh – Die Befestigung deutscher Städte und Residenzen 1600–1625 durch holländische Ingenieuroffiziere. Mitteilungen des Mindener Geschichtsvereins, Jahrgang 46 (1974), S. 9–39.

[:0-4] Helmuth Gericke, Kurt Vogel: De Thiende von Simon Stevin. Das erste Lehrbuch der Dezimalbruchrechnung nach der holländischen und der französischen Ausgabe von 1585. In: Ostwalds Klassiker der exakten Wissenschaften. Band 1. Akademische Verlagsgesellschaft Frankfurt, Frankfurt am Main 1965.

[5] José Ferreirós: Mathematical Knowledge and the Interplay of Practices. Oxford 2016, S. 211.

[6] Hensk J. M. Bos: Simon Stevin, mathématicien. In: Raphaël De Smedt (Hrsg.): Simon Stevin 1548–1620. L'émergence de la nouvelle science. Turnhout 2004, S. 51.