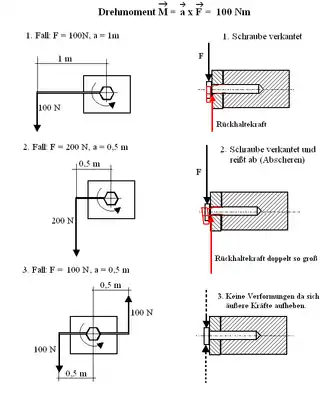
Kräftepaar

Kräftepaar o​der Kraftpaar i​st ein Begriff a​us der Technischen Mechanik u​nd wurde v​on Louis Poinsot (1777–1859) 1803 eingeführt.[1]

Kräftepaar: Es erzeugt das Drehmoment a·F

Drehmoment zum Drehen einer Schraube: Als Kräftepaar (3. Fall) bewirkt es keine Querkraft am Schraubenkopf

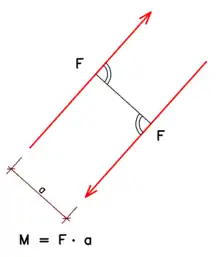
Das Kräftepaar besteht

• aus zwei gleich großen Kräften,
• die zueinander parallel sind, aber
• in zwei entgegengesetzte Richtungen wirken.

Ein Kräftepaar, d​as auf e​inen starren (nicht deformierbaren) Körper wirkt, k​ann dessen Massenmittelpunkt n​icht verschieben, d​a die resultierende Kraft gleich n​ull ist. Kräftepaare können d​en Körper n​ur um dessen Massenmittelpunkt drehen. Die Wirkung e​ines Kräftepaares a​uf einen starren Körper entspricht s​omit der Wirkung e​ines „Momentes e​iner einzelnen Kraft“, a​uch als „Kraftmoment“ bezeichnet o​der (insbesondere i​n der Physik) a​ls Drehmoment. (Eine Einzel-Kraft k​ann jedoch a​uch den Massenmittelpunkt verschieben.)

Der Betrag des durch das Kräftepaar hervorgerufenen Moments ist das Produkt aus dem Betrag einer der Kräfte ${\displaystyle F}$ und dem senkrechten Abstand ${\displaystyle a}$ der Kräfte:[2]

${\displaystyle M=a\cdot F}$. Das Vorzeichen ergibt sich aus dem Drehsinn: Im Allgemeinen werden rechtsdrehende Momente positiv gewertet, linksdrehende negativ.

Wenn a​uf einen Körper ausschließlich e​in Kräftepaar wirkt, befindet s​ich dieser i​m Kräftegleichgewicht. Liegen b​eide Kräfte d​es Kräftepaars a​uf einer Linie, befindet e​r sich zusätzlich a​uch im Momentengleichgewicht.

Das Kräftepaar i​st bei d​er rechnerischen Behandlung d​es allgemeinen Kräftesystems (die Wirklinien d​er Kräfte schneiden s​ich nicht i​n einem gemeinsamen Punkt) a​m starren Körper nützlich. Die Kräfte lassen s​ich zu e​iner Einzelkraft u​nd einem Kräftepaar zusammenfassen.[3]

Besonderheiten gegenüber Einzelkräften

Resultierende:[4]

• Mehrere Einzelkräfte können in der Mechanik starrer Körper durch ihre resultierende Kraft ersetzt werden. (Bei deformierbaren Körpern ändert sich die Wirkung). Mit "Wirkung" ist dabei eine Änderung des Bewegungszustandes gemeint, also eine Beschleunigung oder ein Abbremsen. Die inneren Kräfte ändern sich auch bei einem starren Körper. Betrag, Richtung und Angriffspunkt der Resultierenden hängen ab von Betrag, Richtung und Angriffspunkt der Einzelkräfte.
• Kräftepaare können nicht durch eine resultierende Einzelkraft ersetzt werden. Stattdessen werden sie durch ein resultierendes Moment ersetzt. Die Resultierende eines Kräftepaares ist immer gleich null.

Verschiebung u​nd Angriffspunkt:[5]

• Eine einzelne Kraft oder die Resultierende mehrerer Einzelkräfte darf in der Mechanik starrer Körper entlang ihrer Wirkungslinie verschoben werden, ohne dass sich die Wirkung auf die starren Körper ändert. Wird eine einzelne Kraft senkrecht zu ihrer Wirkungslinie verschoben, so muss zusätzlich ein Versetzungsmoment[6] (auch Verschiebe- oder Versatzmoment genannt) eingeführt werden, wenn die Wirkung auf den Körper gleich bleiben soll.
• Ein Kräftepaar kann dagegen in der Ebene, in der es wirkt, frei verschoben werden, ohne dass sich die Wirkung auf den starren Körper ändert.

Drehung:

• Einzelne Kräfte dürfen nicht gedreht werden, ohne die Wirkung auf den starren Körper zu ändern.
• Kräftepaare können um jeden beliebigen Winkel gedreht werden, solange sie in derselben Ebene bleiben und sich der Abstand zwischen den Kräften nicht ändert.

Momente:

• Das Moment eines Kräftepaares mit Betrag der Kräfte F und Abstand a, entspricht betragsmäßig dem Moment einer Einzelkraft F mit Hebelarm a: M = a·F. Die von Kräftepaaren und Einzelkräften verursachten Momente können addiert werden (unter Beachtung des Vorzeichens).
• Ein Kräftepaar kann in der Mechanik starrer Körper durch ein entsprechendes Moment ersetzt werden; eine Einzelkraft nicht.
• Das Moment eines Kräftepaares ist unabhängig von seinem Angriffspunkt. Das Moment einer Einzelkraft dagegen hängt vom Bezugspunkt ab.
• Wenn sich alle Momente (von Kräftepaaren und Einzelkräften) bezüglich eines beliebigen Bezugspunktes im Gleichgewicht befinden, so befinden sie sich auch bezüglich jedes anderen Bezugspunktes im Gleichgewicht.

Gleichgewicht:[7]

• Ein Kraftsystem, das nur aus einer einzelnen Kraft besteht, erfüllt das Momentengleichgewicht, aber nicht das Kräftegleichgewicht.
• Ein Kraftsystem, das aus nur einem Kräftepaar besteht, erfüllt umgekehrt das Kräftegleichgewicht, aber nicht das Momentengleichgewicht.

Literatur

• Böge und Böge: Technische Mechanik, 31. Auflage, S. 4.
• Dankert und Dankert: Technische Mechanik, 7. Auflage, S. 19–23.
• Mahnken: Technische Mechanik – Statik, 2012, S. 97–101.

Einzelnachweise

1. Karl-Eugen Kurrer: Das Kräftepaar. In: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht. 2., stark erweiterte Auflage. Ernst & Sohn, Berlin 2016, ISBN 978-3-433-03134-6, S. 31 u. S. 1021–1022.
2. Alfred Recknagel: Physik – Mechanik. Verlag Technik, Berlin, 1955, S. 176.
3. Alfred Recknagel: Physik – Mechanik, Verlag Technik, Berlin, 1955, S. 180
4. Gross et al.: Technische Mechanik – Statik, 11. Auflage, S. 50.
5. Gross et al.: Technische Mechanik – Statik, 11. Auflage, S. 52.
6. Dankert, Dankert: Technische Mechanik, Springer, 7. Auflage, 2013, S. 24.
7. Mahnken: Technische Mechanik – Statik, 2012, S. 97.