Oberton

Obertöne (auch Partial-, Teil-, Aliquot-, Neben- oder Beitöne)[1] sind die neben dem Grundton mitklingenden Bestandteile eines musikalisch instrumental oder vokal erzeugten Tones.

Ein solcher ist jedoch im akustischen Sinne kein einzelner Ton (Sinuston),[n 1] sondern ein Klang oder Tongemisch, also ein Schallereignis, das sich vorrangig aus mehreren sinusförmigen Teiltönen von unterschiedlicher Amplitude zusammensetzt. Der tiefste Teilton wird Grundton genannt und bestimmt in der Regel die wahrgenommene Tonhöhe. Die höheren Teiltöne, die Obertöne, erzeugen die Klangfarbe.[n 2]

Bei fast allen natürlichen Musikinstrumenten (mit Ausnahme der Schlaginstrumente) sind die Frequenzen der Obertöne normalerweise ganzzahlige Vielfache der Grundfrequenz. Das bedeutet, dass einem Grundton mit der angenommenen Frequenz von 100 Hz Obertöne mit Frequenzen von 200 Hz, 300 Hz, 400 Hz, 500 Hz, 600 Hz … beigefügt sind. Derartige Teiltöne bezeichnet man auch als Harmonische.

Als Unharmonische bezeichnet man solche Teiltöne, die aus dieser mathematischen Folge herausfallen, (z. B. bei Röhren, Stäben, Platten oder Glocken). Sie entstehen durch Schwingungen, deren Frequenzen keine ganzzahligen Verhältnisse zur wahrgenommenen Grundfrequenz haben. Dadurch wird das Erkennen einer bestimmten Tonhöhe erschwert oder der Ton als unsauber oder misstönend empfunden.

Obertöne sind als Teiltöne Bestandteile eines Gesamtklanges, der durch Eigenschwingungen eines schwingungsfähigen Mediums entsteht. Bei den begrifflich verwandten Naturtönen von Blasinstrumenten werden durch sogenanntes Überblasen einzelne Oberschwingungen so stark angeregt, dass sie direkt als klingende Töne wahrgenommen werden, die ihrerseits weitere Obertöne erzeugen. Gleiches gilt für die Flageoletttöne bei Saiteninstrumenten.

Je nach Schallquelle ist das Klangspektrum ganz spezifisch zusammengesetzt. Daher ist für die charakteristische Klangfarbe von Musikinstrumenten sowie von Menschen- und Tierstimmen neben Rauschanteilen und Faktoren im zeitlichen Verlauf des Signals vor allem der Obertongehalt verantwortlich. Stimm- und instrumententypische Frequenzbereiche, in denen die Obertöne durch Resonanz besonders verstärkt werden und daher vorrangig für die Klangfarbe ausschlaggebend sind, heißen Formanten.

Harmonische

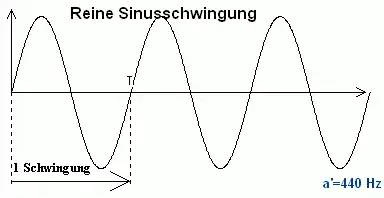
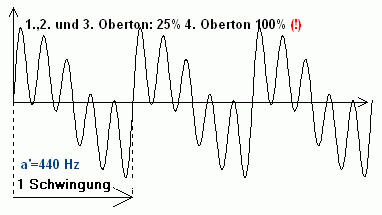
Als Harmonische bezeichnet man die Teiltöne eines harmonischen Klangs, also dessen Grundton und die Obertöne, deren Schwingungszahlen ganzzahlige Vielfache der Frequenz des Grundtons sind. In der folgenden Abbildung stellt die große Sinuswelle links den Grundton dar; im Bild rechts daneben überlagern harmonische Obertöne in Form schmalerer Sinuswellen die große Welle.

	Der 4. Oberton cis⁴ allein

Hörbeispiel: Aufbau eines harmonischen Klangs aus Sinustönen

Im nebenstehenden Hörbeispiel wird ein harmonischer Klang sukzessive aus seinen elektronisch erzeugten sinusförmigen Teiltönen aufgebaut. Die subjektiv wahrgenommene Lautstärkezunahme des 4. Oberton, bei objektiv gleichen Dezibel, ist auf die Hörschwelle zurückzuführen.

Harmonische Schwingungen stehen immer in Beziehung zur Grundfrequenz. Wie genau diese Beziehung beschrieben wird, hängt vom gewählten mathematischen Modell ab. Die Wahl der Grundfrequenz ist objektiv schwierig und wird in Bezug auf Musik in erster Linie vom empfundenen oder notierten Grundton bestimmt. Bei der Analyse oder Synthese von Schallereignissen kann aus akustischer oder messtechnischer Sicht die Grundfrequenz auch anders gewählt werden. Grundton und Obertöne müssen daher immer im Kontext verstanden werden.

In vielen Fällen reicht jedoch ein einfaches Beschreibungsmodell, das die Frequenzen der Oberschwingungen als ganzzahlige Vielfache einer als Ton wahrgenommenen Grundfrequenz annimmt.

Erläuterungsbeispiel: Kammerton a¹ und die ersten fünf Harmonischen

Diese Tabelle zeigt den Kammerton a¹ als Grundton und seine ersten vier Obertöne mit ihrer jeweiligen Ordnung n und ihren Frequenzen. Die n. Harmonische hat allgemein die Frequenz n·f.

Harmonische Reihe
Frequenz	1·f = 440 Hz	2·f = 880 Hz	3·f = 1320 Hz	4·f = 1760 Hz	5·f = 2200 Hz
Notenbezeichnung	a¹	a²	e³	a³	cis⁴
Ordnung	n = 1	n = 2	n = 3	n = 4	n = 5
	Grundfrequenz	1. Oberton	2. Oberton	3. Oberton	4. Oberton
	1. Teilton	2. Teilton	3. Teilton	4. Teilton	5. Teilton
	1. Harmonische	2. Harmonische	3. Harmonische	4. Harmonische	5. Harmonische[n 2]

Man sieht hier: Das Intervall [a² e³] ist eine Quinte mit dem Frequenzverhältnis ^3·f/_2·f = ³/₂ und das Intervall [a³ cis⁴] ist eine große Terz mit dem Frequenzverhältnis ^5·f/_4·f = ⁵/₄.

Das einfache harmonische Modell – Obertonreihe

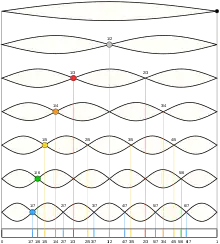
Harmonische Teilschwingungen einer idealisierten Saite

Bereits seit der Antike gewinnt man Erkenntnisse zu Obertönen am Beispiel schwingender Saiten. Dabei wird angenommen, dass eine auf die Hälfte verkürzte Saite einen Ton mit der doppelten Schwingungszahl liefert, eine auf ein Drittel reduzierte Saite die dreifache Schwingungszahl ergibt usw. Für die musikalische Praxis, etwa das Überblasen von Blasinstrumenten, das Spielen von Flageoletttönen auf Saiteninstrumenten, den Obertongesang oder die Orgelregistrierung, ist dieses einfache Modell in der Regel ausreichend. Bei der Anwendung auf andere Klangquellen, wie z. B. stark gespannte Klaviersaiten, stößt dieses Modell jedoch an seine Grenzen.

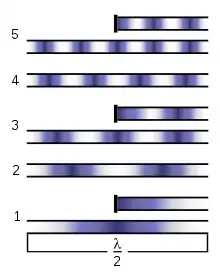
Die nebenstehende Abbildung stellt (in willkürlicher Beschränkung auf die ersten sieben) die Eigenschwingungen einer Saite dar. Unter bestimmten Bedingungen kann die Saite jede dieser Eigenschwingungen separat (Flageoletttöne) ausführen, in der Regel werden jedoch alle oder zumindest mehrere dieser Eigenschwingungen gleichzeitig angeregt, sodass die resultierende Schwingung aus einer komplexen Überlagerung dieser Teilschwingungen besteht.

Das menschliche Gehör nimmt periodische Schwingungen als Töne (im Sinne von musikalischen Tönen) wahr, wobei die Schwingungsperiode die wahrgenommene Tonhöhe bestimmt. Analysiert man das Amplitudenspektrum eines Audiosignals einer annähernd periodischen Schwingung z. B. mit Hilfe der Kurzzeit-Fourier-Transformation, so besteht dieses aus

einem Grundton, der der Schwingungsperiode entspricht
und den harmonischen Obertönen mit Frequenzen, die ganzzahlige Vielfache der Grundfrequenz sind.

Listet man die Teiltöne im Sinne zunehmender Frequenz auf, so erhält man die Teil- bzw. Obertonreihe:

Die Obertonreihe

Im Folgenden sind beispielhaft die ersten sechzehn auf den Grundton C bezogenen Teiltöne dargestellt. Diese Beschränkung ist aus Gründen der Überschaubarkeit willkürlich gewählt. Theoretisch setzt sich die Teiltonreihe nach oben mit immer kleiner werdenden Abständen bis ins Unendliche fort.

Als Notenbeispiel

Bei notenmäßiger Darstellung der Teiltöne ist zu berücksichtigen, dass wegen der nach oben kontinuierlich abnehmenden Tonabstände eine exakte Wiedergabe in Notenschrift (zumindest im höheren Bereich der Teiltonreihe) nur annähernd (und schließlich gar nicht mehr) möglich ist. Auch stimmen nicht alle Obertöne mit den Tonstufen der gängigen Stimmungssysteme überein. Im folgenden Notenbeispiel werden die Obertöne mit den Tönen der gleichstufigen Stimmung verglichen. Die Abweichungen nach oben oder unten sind jeweils in Cent angegeben.

Während bei der gleichstufigen Stimmung außer dem Grundton und dessen Oktaven kein Ton exakt mit der Teiltonreihe übereinstimmt, gibt es keine Abweichungen bei reiner Stimmung bei allen Teiltönen außer Nr. 7 (Naturseptime), Nr. 11 (Alphorn-Fa), Nr. 13, Nr. 14 (Oktave der Naturseptime) und Nr. 15.

Als Tabelle

Die in der Tabelle verwendeten Farben orientieren sich an der Musik-Farben-Synästhesie.

Einfaches Modell – Vergleich mit Grundton
Grundton – Oberton Nr:	Grundton	1	2	3	4	5	6	7	8	09	10	11	12	13	14	15
Teilton Nr:	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Vielfaches der Grundfrequenz:	einfache	doppelte	dreifache	vierfache	fünffache	sechsf.	siebenf.	achtf.	neunf.	zehnfache	elffache	zwölffache	dreizehnf.	vierzehnf.	fünfzehnf.	sechzehnf.
Beispiel f in Hz:	66[T 1]	132	198	264	330	396	462	528	594	660	726	792	858	924	990	1056
Note:
Tonname:	C	c	g	c¹	e¹	g¹	≈ b¹[T 2]	c²	d²	e²	≈ f²[T 3]	g²	≈ as²[T 4]	≈ b²[T 5]	h²	c³
Verhältnis zum Ton darunter:	1:1	2:1	3:2	4:3	5:4	6:5	7:6	8:7	9:8	10:9	11:10	12:11	13:12	14:13	15:14	16:15
Intervall zum Ton darunter:	Prime	Oktave[T 6]	reine Quinte	reine Quarte	große Terz	kleine Terz	–	–	großer Ganzton	kleiner Ganzton	–	–	–	–	–	diatonischer Halbton

Tabellenfußnoten

Eine kleine Terz (Frequenzverhältnis ⁶⁄₅) über dem Kammerton a′ mit 440 Hz liegt der Ton c² mit 528 Hz. Das drei Oktaven tiefer liegende C hat demnach die Frequenz von 66 Hz.
7. Oberton = 462 Hz (Naturseptime). Abweichung von b¹ = 475,2 Hz der reinen Stimmung ≈ 49 Cent. Hinweis: Vor allem für die Darstellung der feinen Größenunterschiede der Intervalle verwendet man die Einheit Cent, wobei ein gleichstufiger Halbton 100 Cent und eine Oktave 1200 Cent entsprechen. Die Berechnung erfolgt über den Logarithmus des Frequenzverhältnisses zur Basis 2. Hier 1200 log₂ (475,2/462) ≈ 49 Cent.
11. Oberton = 726 Hz (Alphorn-Fa). Abweichung von f² = 704 Hz bzw. fis² = 742,5 Hz der reinen Stimmung ≈ 53 Cent bzw. 39 Cent.
13. Oberton = 858 Hz. Abweichung von as² = 844,8 Hz der reinen Stimmung ≈ 27 Cent.
14. Oberton = 924 Hz (Naturseptime). Abweichung von b² = 950,4 Hz der reinen Stimmung ≈ 49 Cent.
Das musikalische Intervall einer Oktave entspricht einer Verdopplung der Frequenz.

Aus der letzten Zeile der Tabelle wird ersichtlich, dass sich alle Intervalle der diatonischen Tonleiter (siehe reine Stimmung) aus der Obertonreihe herleiten lassen. Insbesondere: Halbton (Frequenzverhältnis ¹⁶⁄₁₅), großer und kleiner Ganzton (⁹⁄₈ und ¹⁰⁄₉), kleine Terz (⁶⁄₅), große Terz (⁵⁄₄), Quart (⁴⁄₃), Quint (³⁄₂) und Oktave (²⁄₁).

Grenzen des einfachen Modells

Bei vielen Musikinstrumenten oder bei Vokalen der menschlichen Stimme besteht ein wesentlicher Teil des Klangs aus periodischen Schwingungen, die sich mit der vereinfachten Modellvorstellung von Grundton und harmonischen Obertönen in guter Näherung beschreiben lassen, so beispielsweise bei schwingenden Saiten von Saiteninstrumenten (Chordophonen) oder schwingenden Luftsäulen von Blasinstrumenten (Aerophonen). Jedoch treten dabei in der Realität mehr oder weniger starke Abweichungen von der theoretischen Ganzzahligkeit der Obertöne auf.

Inharmonizität

Abweichungen von den harmonischen Verhältnissen der Teiltöne treten bei vielen Instrumenten auf. Diese unter dem Begriff Inharmonizität bekannten Abweichungen werden zum Beispiel beim Klavier im Wesentlichen durch das Biegemoment der Saite hervorgerufen.[2] Besonders die dicken Basssaiten sind hiervon betroffen. Höhere Obertöne sind stärker betroffen als niedrigere.[2] Die genauere Analyse derartiger Obertöne ist aufwändiger und erfordert zur Beschreibung komplexere Modelle als die Analyse und Beschreibung von „sehr harmonischen“ Tönen. (Siehe auch Audiosignal.)

Geräuschanteile

Außerdem treten auch nicht-periodische Schwingungen auf, die ein eher breitbandiges Frequenzspektrum besitzen und sich nicht durch Grundton und harmonische Obertöne beschreiben lassen, z. B. Anschlaggeräusche bei Saiteninstrumenten, Anblasgeräusche bei Blasinstrumenten und Orgelpfeifen sowie Konsonanten bei der menschlichen Stimme. Die Analyse dieser Klangkomponenten erfordert moderne elektronische Messtechnik und mathematische Modelle, deren Lösungen nur mit leistungsfähigen Computern berechenbar sind.

Unschärfe

Mathematisch sind Schwingungen nur dann sinusförmig, wenn sie sowohl schon unendlich lange andauern als auch noch unendlich lange andauern werden. Schwingungen sind in der Praxis immer nur quasiperiodisch oder fastperiodisch.[3] Die Sinusfunktion erstreckt sich beidseitig in die Unendlichkeit und ein Abschneiden der Dauer führt mathematisch zu etwas anderem, einer zeitlich begrenzten Welle. In psychoakustischer Konsequenz ergeben sich beim Abschneiden von langandauernden kontinuierlichen, statischen Sinustönen oder Sinustongemischen breitbandige Artefakte.[4]

Bei kurzandauernden Vorgängen solcher Art – wie sie bei allen Instrumenten auftreten, bei denen nicht stets Energie nachgereicht wird, also vor allem bei den Zupf- und Schlaginstrumenten (auch beim Klavier) – ist die Grundvoraussetzung des Dauertones nicht einmal näherungsweise erfüllt.

In der Kultur der Ingenieurwissenschaften ging man meistens von der Situation aus, dass Vorgänge langandauernd und langsam veränderlich sind (bei der Modulation eines Radiosenders ist dies der Fall). Nur dann ergeben die Fouriertransformation und die daraus implizit im Artikel folgenden Begriffe einen Sinn. Erst um die Wende zum 21. Jhdt. hat sich die Einsicht durchgesetzt, dass bei schnell veränderlichen und kurz andauernden Vorgängen die Wavelet-Transformation Anwendung finden muss, worauf Begriffe wie etwa „Frequenz“ neu gedeutet werden müssen. Zur Grundtonerkennung sind seitdem eine Vielfalt verschiedener Methoden in Verwendung.[5]

Musik beinhaltet wesentlich solche Vorgänge. Insofern ist auch aus dieser Sicht Kritik an überkommenen Vorstellungen zu üben. Zu sehr sind unsere Vorstellungen von den für die Elektronik in weiten Bereichen vollständig ausreichenden heute verbreiteten Modellen geprägt. Dass man sich der komplexen Zusammenhänge bereits bewusst war, bevor Hermann von Helmholtz eine mathematische Theorie zur Erklärung der Klangfarbe durch Obertöne in Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik (1863) veröffentlichte, zeigt ein Auszug aus Zamminers Die Musik und die musikalischen Instrumente von 1885: „Alle tönenden Körper, welches ihre Substanz, ihre Gestalt, ihr Elasticitäts- und Spannungszustand sein möge, sind außer den Schwingungen in ganzer Masse, welche den Grundton geben, noch unendlich vieler Abtheilungsarten und eben so vieler Obertöne fähig. Die Schwingungszustände, welche sie anzunehmen vermögen, sind um so mannichfaltiger, je weniger einfach ihre Form ist. Nur cylindrische und prismatische Luftsäulen und ähnlich wie diese schwingende Stäbe von geringem Durchmesser haben eine so einfache harmonische Oberreihe wie die gespannten Saiten; weit reicher schon ist die Menge der Obertöne bei Körpern, welche, wie Platten und gespannte Häute, sich in ebener oder gekrümmter Fläche ausbreiten, am Mannichfaltigsten die von beliebig in jedem Sinne ausgedehnten festen Massen und Lufträumen.“[6]

Obertöne und Klangfarbe

Obertöne der menschlichen Stimme

In der menschlichen Stimme schwingt, genau wie in den meisten klangerzeugenden physikalischen Systemen, ein komplexes Obertonspektrum mit. In der besonderen Gesangstechnik des Obertongesangs kann man diese hohen Frequenzen zum Dominieren bringen.

Der unterschiedliche Klang von Vokalen kommt durch deren spezifischen Obertonaufbau zustande. Durch die individuelle Größe und Form von Mund und Rachen werden manche Frequenzen durch Resonanz verstärkt, andere gedämpft. Die Frequenzbereiche, die jeweils verstärkt werden, nennt man auch Formanten.

Obertöne unterschiedlicher Instrumente

Wellen in offenen und gedackten Röhren. Die Wellenknoten sind blau.

Der spezifische Klang eines Instrumentes ergibt sich aus den Antworten auf folgende Fragen:

Welche Obertöne sind überhaupt vorhanden?
Wie laut sind diese Obertöne im Verhältnis zueinander?
Wie ändern sich die Lautstärke und Frequenz der einzelnen Obertöne, während der Ton erklingt?
Welche Nebengeräusche (Anschlaggeräusche, Blasgeräusche …) kommen hinzu?

Folgende Instrumente haben einen besonders charakteristischen Teiltonaufbau:

Streichinstrumente besitzen ein sehr reichhaltiges Teiltonspektrum.
Klarinetten betonen die Lautstärke der ungeraden Teiltöne.
Beim Fagott ist der Grundton sehr viel schwächer als die ersten Obertöne.
Glocken betonen oftmals die Terzen sehr stark und die Obertonzusammensetzung ist komplex.
Stimmgabeln erzeugen fast nur den Grundton.

Bei Instrumenten mit einfachen Obertonzusammensetzungen sind die Frequenzen der Obertöne annähernd ganzzahlige Vielfache der Frequenz des Grundtons. Hierzu gehören die Chordophone (Saiteninstrumente) und die Aerophone mit schwingender Luftsäule. Das ist natürlich auch nur eine idealisierte Annahme; so besteht bei wirklichen (nicht unendlich dünnen) Saiten eine Inharmonizität. Gerade die sehr geringen Abweichungen von den idealen Harmonischen machen den Klang eines einzelnen Instrumentes unverwechselbar und lebendig.

Bei den meisten Holzblasinstrumenten ist das sehr nahe der idealisierte Annahme, auch für viele Saiteninstrumente stimmt dies recht gut. Beim Klavier allerdings ist das ganzzahlige Frequenzverhältnis nur annähernd erfüllt. Besonders die sehr hohen Obertöne liegen schon recht weit neben den Frequenzen mit ganzzahligen Verhältnissen zum Grundton. Je höher man die Leiter der Obertöne emporsteigt, desto mehr weichen deren Frequenzen von den genau harmonischen ab. Es hat sich sogar herausgestellt, dass die dem Klavier eigene Klangfarbe sehr wesentlich mit dieser Abweichung von den genau harmonischen Obertönen zusammenhängt. Z. B. hören sich Imitationen eines Klaviers nicht besonders klavierähnlich an, wenn diese Abweichung der Obertonreihe bei der künstlichen Erzeugung des Tones nicht mitberücksichtigt wird.

Die Eigenfrequenzen und deren harmonische Obertöne hängen vom jeweiligen Klangerzeuger ab und werden durch die Abmessungen und Beschaffenheit des Körpers bestimmt. Es gibt Instrumente, bei denen sich die Obertonzusammensetzungen relativ einfach beschreiben lassen, und andere, die sehr komplexe Beschreibungsmodelle erfordern. Bei Instrumenten mit komplexen Obertonzusammensetzungen stehen viele Frequenzen der Obertöne in komplizierten nichtganzzahligen Verhältnissen zueinander. Die Obertöne der Membranophone mit runder Membran haben die Eigenfrequenzen einer Besselschen Differentialgleichung. Bei Idiophonen können sich je nach der Form des Klangkörpers ganz unterschiedliche Obertonreihen ergeben – bei den Stabspielen etwa sind es die Eigenfrequenzen der Biegeschwingung eines Balkens.

Künstlich aus Sinustönen hergestellte Obertonspektren nennt man synthetische Klänge (siehe Klangsynthese, Synthesizer). Eine reine Sägezahnschwingung zeichnet sich dadurch aus, dass sie zum Grundton alle seine Obertöne enthält, weshalb man sie zu den Zeiten der analog-elektronischen Musikinstrumente bevorzugt als Ausgangsschwingung einsetzte.

Wirkung der Obertöne: Brillanz und Dumpfheit

Der Anteil der Obertöne am Gesamtspektrum und die daraus resultierende Klangfarbe kann durch Worte wie Brillanz, Schärfe, Reinheit, Dumpfheit u. a. beschrieben werden.

Im Allgemeinen klingen Töne umso brillanter (Violine), schärfer (Trompete) oder farbiger (Oboe, Fagott), je mehr Obertöne sie haben, und umso reiner und klarer (Flöte) bzw. blasser oder dumpfer (tiefe Klarinette, gedeckte Orgelregister), je weniger sie haben.

Reine Töne ohne Obertöne, also Sinustöne, können praktisch gar nicht erzeugt werden. Näherungsweise können sie auf mechanischem Wege nur mit sehr geringen Schallpegeln erzeugt werden (Stimmgabel oder Hohlraumresonatoren, sehr sanft angeregt). Elektronisch ist die Erzeugung näherungsweise reiner Sinustöne problemlos möglich. Sie klingen bei tieferer Frequenz dumpf, breit und strömend, bestimmte Orgelregister kommen dem nahe. Bei höheren Frequenzen wird der Unterschied zu Klängen mit Obertönen geringer, weil diese Obertöne außerhalb des Hörbereichs liegen. Ein Beispiel der Situation für mittlere Frequenzen ist der 1000-Hertz-Ton des Fernsehtestbilds, wobei der Lautsprecher jedoch durch seine Verzerrungen schon wieder sein eigenes Obertonspektrum hinzufügt. Da die gesamte Energie nur in einem schmalen Frequenzbereich auftritt, können pegelstarke Sinustöne sehr unangenehm sein. Überhaupt sind Sinustöne ein Prüfstein für jeden Lautsprecher, da die Gefahr von elektrischer und mechanischer Überlastung einerseits sehr hoch ist, andererseits Verzerrungsprodukte mit hörbaren Pegeln sofort auffallen und mechanische Konstruktionsprobleme mit bisweilen schnarrenden oder fauchenden Resonanzen offengelegt werden.

In einem Mehrweg-Lautsprecher (Elektroakustik) ist in erster Linie der Hochtöner für die Brillanz, also für die Klanghelligkeit und die Klangfarbe der Wiedergabe, zuständig.

Höhere Obertöne sind bei mechanischen Musikinstrumenten in der Regel leiser (pegelschwächer) als tiefere:

Zum einen werden bei mechanischen Tonerzeugern höhere Frequenzen nur wesentlich schwächer angeregt als tiefere (z. B. nimmt bei einer schwingenden Saite die Schwingungsamplitude der Obertöne mit steigender Frequenz ab).
Zum anderen werden höhere Frequenzen in der Luft stärker gedämpft. Daher ist bei einer Beschallung über große Flächen die Brillanz der Wiedergabe meistens relativ schlecht.

Hörbarkeit von Obertönen

In der Regel werden Obertöne nicht einzeln wahrgenommen, sondern ergeben den Klang eines Tons. In bestimmten Fällen oder unter besonderen Bedingungen können sie aber auch einzeln gehört oder hörbar gemacht werden.

Manche Menschen sind in der Lage, aus einem Klang einzelne Obertöne auch ohne jegliche Hilfe selektiv herauszuhören. Dieses gilt besonders bei sehr stabilen Tönen wie beispielsweise bei lang ausgehaltenen Tönen von Orgelpfeifen.
Die Gesangstechnik des Obertonsingens macht die Obertöne deutlich wahrnehmbar. Beispiele sind der Obertongesang mongolischer und tuvinischer Völker. Auch in der westlichen Musik gibt es seit Ende der 1960er Jahre wieder eine Belebung der Obertonkultur.
Auch im instrumentalen Bereich kann man Obertöne deutlich hörbar machen. Typische Instrumente hierfür sind z. B. das Didgeridoo, die Fujara oder Klangschalen.
Bei Saiteninstrumenten können Töne in der Tonhöhe von Obertönen durch Flageolett-Spielweise (siehe Flageolettton) erzeugt werden. Dabei wird die Saite mit der Greifhand nur leicht berührt anstatt sie auf das Griffbrett zu drücken. Allerdings erklingt dann meist ein anderer Ton als bei normalem Greifen.
Auf dem Klavier kann man Obertöne auf drei Arten hörbar machen:
1. Indem man die Tasten eines Akkords aus der Obertonreihe sanft niederdrückt, ohne dass die Hämmer die Saite berühren, und dann den Grundton im Bassbereich kurz und stark anschlägt. Die Obertöne erzeugen nun eine Resonanz auf den ungedämpften Saiten der niedergedrückt gehaltenen Tasten, die man deutlich hören kann.
2. Indem man eine Taste im Bassbereich auf die beschriebene Weise stumm niederdrückt und dann einen oder mehrere Töne aus der zugehörigen Obertonreihe kurz und kräftig anschlägt. Durch Resonanz wird die ungedämpfte Basssaite angeregt, mit den Frequenzen dieser Obertöne zu schwingen. Die angeschlagenen Töne klingen echoartig weiter, obwohl die zugehörigen Saiten abgedämpft wurden.
3. Auch am Klavier kann man einen Flageolettton erzeugen. Dafür drückt man leicht auf den erforderlichen Punkt auf einer Saite und schlägt mit der anderen Hand die entsprechende Taste an. Das Gleiche funktioniert auch mittels Präparierung der Saite, das beste Material dafür ist Gummi.

Insbesondere der erste Effekt wird auch von Komponisten in ihren Werken verwendet (z. B. Béla Bartók: Mikrokosmos, Band IV).

Anwendungen

Die Orgel und ihre Register

Besonders wichtig ist die harmonische Obertonreihe bei der Orgel. Durch verschiedene Orgelregister, die jeweils einzelne bis auf wenige Ausnahmen harmonische Obertöne erzeugen (Aliquoten), lassen sich Klangfarben durch eine einfache Art additiver Synthese erzeugen. Bei Pfeifenorgeln ist nur ein „an“ oder „aus“ der Register möglich. Die am meisten verwendeten harmonischen Obertöne sind dabei Oktaven (2., 4., 8., 16., … Partialton), Quinten (3., 6., 12., … Partialton) und große Terzen (5., 10., … Partialton), in modernen Orgeln auch die kleine Septime (7., 14., … Partialton) und die große None (9., 18., … Partialton).

Eine davon inspirierte Klangsynthese findet bei der Hammond-Orgel statt. Hierbei lassen sich die Anteile der Teiltöne durch Schieberegler zusätzlich variieren.

Residualtöne

Das menschliche Hörzentrum ist in der Lage, zu einem (auch nur teilweise) erklingenden Obertonspektrum die Grundfrequenz wahrzunehmen, auch wenn diese nicht erklingt. Diesen „hinzugefügten“ Grundton bezeichnet man auch als Residualton.

Musiktheorie und -didaktik

Die Existenz von Obertönen wurde seit langer Zeit zu einer wissenschaftlichen Erklärung und Begründung von Tonsystemen der Musik herangezogen, wobei in der Regel von dem einfachen Modell ganzzahliger Frequenz- oder Saitenlängenverhältnisse ausgegangen wurde.

Die erste im Zusammenhang mit Obertönen stehende Theorie wird Pythagoras zugerechnet, dies war vor rund 2500 Jahren.
Für didaktische Zwecke (Lehre der Begleitung, Generalbass, Harmonie und Melodie sowie Kompositionslehre) hat sich wohl als erster Johann Bernhard Logier (1777–1846) die Obertonreihe zunutze gemacht. Seine Lehre von den „harmonisch mitklingenden“ Tönen war zu seinen Lebzeiten stets umstritten; seine didaktisch hoch reflektierten Werke mit ihren einfachen, aufeinander aufbauenden Grundregeln dürfen jedoch als Anfang der modernen, noch heute gültigen Musiktheorie gelten.[7]
Einen der letzten Versuche zur Begründung eines theoretischen Systems aus der Obertonreihe und anderen akustischen Erscheinungen (z. B. Kombinationstönen) findet man bei Paul Hindemith in seiner Unterweisung im Tonsatz. Auch Hindemiths System ist in der Fachwelt sehr umstritten. Reale Töne oder Klänge sind auch heute nur begrenzt mathematisch erfassbar, daher stößt jedes System irgendwann an seine Grenzen. Ein ästhetisches System ist daher nur schwer naturwissenschaftlich zu legitimieren.

Untertonreihen

Spiegelt man die harmonische Obertonreihe, entsteht die theoretische, zu ihr symmetrische harmonische Untertonreihe, die durch Frequenzteilung entsteht, nach unten hin ergänzt. In der Natur sind Untertöne höchst selten; sie treten manchmal bei Glocken und Gongs auf. Es ist nicht sicher, ob es sich tatsächlich um Töne einer Untertonreihe handelt. Praktisch werden sie beim Trautonium, beim Subharchord und beim Untertongesang erzeugt.

Im Besonderen Hugo Riemann gebrauchte den Begriff der Untertonreihe häufig in seinen Lehrbüchern und musikwissenschaftlichen Traktaten, und legte sie in der „Zwei-Wurzel-Theorie“ (Dur/Moll-Dualismus) als Grundlage seiner Funktionstheorie aus.

Anmerkungen

Reine Sinustöne können nur mit elektronischen Mitteln erzeugt werden. Mit Stimmgabeln oder Flöten können aber Schallereignisse hervorgebracht werden, die Sinustönen sehr nahekommen.
Bei den Bezeichnungen „Teilton“ und „Partialton“ wird die Grundfrequenz mitgezählt. Spricht man von „Oberton“, wird die Grundfrequenz nicht mitgezählt. Die Ordnungszahl eines Obertons ist also immer um eins kleiner als die Ordnungszahl eines Teiltons.

Siehe auch

Literatur

Hermann von Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik. Vieweg, Braunschweig 1863, (online).
Stichwort Obertöne. In: Johannes Kunsemüller (Hrsg.): Meyers Lexikon der Technik und exakten Naturwissenschaften. Bibliographisches Institut AG, Mannheim 1970, S. 1844.
Stichwort Teiltöne. In: Willibald Gurlitt, Hans Heinrich Eggebrecht (Hrsg.): Riemann Musik Lexikon (Sachteil). B. Schott’s Söhne, Mainz 1967, S. 942 f.
Stichwort Obertöne. In: Marc Honegger, Günther Massenkeil (Hrsg.): Das große Lexikon der Musik. Band 6: Nabakov – Rampal. Aktualisierte Sonderausgabe. Herder, Freiburg im Breisgau u. a. 1987, ISBN 3-451-20948-9, S. 82 ff.
John R. Pierce: Klang. Musik mit den Ohren der Physik. Spektrum, Heidelberg/Berlin/Oxford 1999, ISBN 3-8274-0544-0.
Markus Fritsch, Katrin Jandl, Peter Kellert, Andreas Lonardoni: Harmonielehre & Songwriting. LEU-Verlag, 8. Auflage 2020. ISBN 3-928825-23-2, S. 60

Weblinks

Einzelnachweise

Eintrag in Meyers Großem Konversations-Lexikon von 1905.
Sam Howison: Practical Applied Mathematics. Modeling, Analysis, Approximation. 2005, ISBN 0-521-60369-2, Kapitel 15.3, Seite 209 ff.
Martin Neukom: Signale, Systeme und Klangsynthese. Grundlagen der Computermusik. Band 2 von Zürcher Musikstudien. 2005, ISBN 3-03910-819-0, Seite 56, online.
Ulrich Karrenberg: Signale – Prozesse – Systeme. Eine multimediale und interaktive Einführung in die Signalverarbeitung. 2009, ISBN 3-642-01863-7, Seite 84, online.
Johann-Markus Batke: Untersuchung von Melodiesuchsystemen sowie von Verfahren zu ihrer Funktionsprüfung. 2006, ISBN 3-86727-085-6, Seite 71, online.
Friedrich Georg Karl Zamminer: Die Musik und die musikalischen Instrumente in ihrer Beziehung zu den Gesetzen der Akustik. 1855, Seite 176, online.
Vgl. vor allem: J. B. Logier: System der Musik-Wissenschaft und der praktischen Composition mit Inbegriff dessen, was gewöhnlich unter dem Ausdrucke General-Bass verstanden wird. Berlin 1827, S. 11: Quintenzirkel, S. 15 ff. Generalbass, ab S. 53 beginnt die Lehre der Obertöne.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Grundfrequenz-4] Eine kleine Terz (Frequenzverhältnis ⁶⁄₅) über dem Kammerton a′ mit 440 Hz liegt der Ton c² mit 528 Hz. Das drei Oktaven tiefer liegende C hat demnach die Frequenz von 66 Hz.

[Naturseptime-5] 7. Oberton = 462 Hz (Naturseptime). Abweichung von b¹ = 475,2 Hz der reinen Stimmung ≈ 49 Cent. Hinweis: Vor allem für die Darstellung der feinen Größenunterschiede der Intervalle verwendet man die Einheit Cent, wobei ein gleichstufiger Halbton 100 Cent und eine Oktave 1200 Cent entsprechen. Die Berechnung erfolgt über den Logarithmus des Frequenzverhältnisses zur Basis 2. Hier 1200 log₂ (475,2/462) ≈ 49 Cent.

[Alphorn-Fa-6] 11. Oberton = 726 Hz (Alphorn-Fa). Abweichung von f² = 704 Hz bzw. fis² = 742,5 Hz der reinen Stimmung ≈ 53 Cent bzw. 39 Cent.

[as-7] 13. Oberton = 858 Hz. Abweichung von as² = 844,8 Hz der reinen Stimmung ≈ 27 Cent.

[Naturseptime2-8] 14. Oberton = 924 Hz (Naturseptime). Abweichung von b² = 950,4 Hz der reinen Stimmung ≈ 49 Cent.

[Oktve-9] Das musikalische Intervall einer Oktave entspricht einer Verdopplung der Frequenz.

[Sinus-2] Reine Sinustöne können nur mit elektronischen Mitteln erzeugt werden. Mit Stimmgabeln oder Flöten können aber Schallereignisse hervorgebracht werden, die Sinustönen sehr nahekommen.

[verh-3] Bei den Bezeichnungen „Teilton“ und „Partialton“ wird die Grundfrequenz mitgezählt. Spricht man von „Oberton“, wird die Grundfrequenz nicht mitgezählt. Die Ordnungszahl eines Obertons ist also immer um eins kleiner als die Ordnungszahl eines Teiltons.

[1] Eintrag in Meyers Großem Konversations-Lexikon von 1905.

[Practical_Applied_Mathematics_2005-10] Sam Howison: Practical Applied Mathematics. Modeling, Analysis, Approximation. 2005, ISBN 0-521-60369-2, Kapitel 15.3, Seite 209 ff.

[11] Martin Neukom: Signale, Systeme und Klangsynthese. Grundlagen der Computermusik. Band 2 von Zürcher Musikstudien. 2005, ISBN 3-03910-819-0, Seite 56, online.

[12] Ulrich Karrenberg: Signale – Prozesse – Systeme. Eine multimediale und interaktive Einführung in die Signalverarbeitung. 2009, ISBN 3-642-01863-7, Seite 84, online.

[13] Johann-Markus Batke: Untersuchung von Melodiesuchsystemen sowie von Verfahren zu ihrer Funktionsprüfung. 2006, ISBN 3-86727-085-6, Seite 71, online.

[14] Friedrich Georg Karl Zamminer: Die Musik und die musikalischen Instrumente in ihrer Beziehung zu den Gesetzen der Akustik. 1855, Seite 176, online.

[15] Vgl. vor allem: J. B. Logier: System der Musik-Wissenschaft und der praktischen Composition mit Inbegriff dessen, was gewöhnlich unter dem Ausdrucke General-Bass verstanden wird. Berlin 1827, S. 11: Quintenzirkel, S. 15 ff. Generalbass, ab S. 53 beginnt die Lehre der Obertöne.