Kippschwingung

Als Kippschwingung oder Sägezahnschwingung wird eine besondere Form periodischer, nicht-sinusförmiger Schwingungen bezeichnet. Im Gegensatz zur harmonischen Schwingung, bei denen Hin- und Herbewegung symmetrisch ablaufen, folgt bei der Kippschwingung einer langsamen Aufladung eine sehr schnelle Entladung, die typisch für einen Vorgang ist, bei dem die Entladung mit einem Mal durch das Erreichen eines Schwellenwertes ausgelöst wird. Entsprechend dem Aussehen ihrer grafischen Darstellung wird sie auch „Sägezahnschwingung“ genannt. Die Kurve der Kippschwingung ist im Allgemeinen aufsteigend, d. h., dass das Signal kontinuierlich ansteigt, um dann abrupt abzufallen.

Schematischer Graph einer Kippschwingung

Mathematische Beschreibung

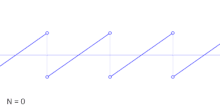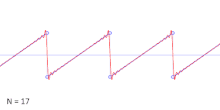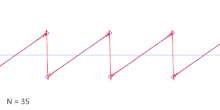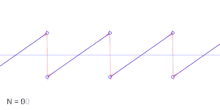
Sägezahnschwingung als Überlagerung von unterschiedlicher Anzahl von Harmonischen. (Fourier-Synthese)

(gerade und ungerade) Harmonische einer Sägezahnschwingung von 1000 Hz

Die ideale Kippschwingung lässt sich als eine abschnittsweise stetige und lineare Funktion mit dem Parameter t ohne Skalierungsfaktoren ausdrücken als

x(t)=t-\lfloor t\rfloor \,

wobei der Ausdruck $\lfloor t\rfloor$ die Gaußklammer (Abrundungsfunktion) darstellt. Im Englischen wird dafür auch die Bezeichnung floor(t) verwendet.

Wie eine große Klasse periodischer Funktionen lässt sich dieser Sägezahnverlauf in einer dazu gleichwertigen Darstellung mittels Fourierreihe ausdrücken:

x(t)=-{\frac {1}{\pi }}\cdot \sum _{k=1}^{\infty }{\frac {\sin(2\pi kt)}{k}}+{\frac {1}{2}}

oder allgemeiner und um den Nullpunkt zentriert:

x(t)=-{\frac {2c}{\pi }}\cdot \sum _{k=1}^{\infty }{\frac {\sin(2\pi kft)}{k}}

mit einem Skalierungsfaktor c ≠ 0. Erwähnenswert ist, dass bei der Sägezahnfunktion geradzahlige und ungeradzahlige Vielfache der Grundfrequenz f im Spektrum auftreten.

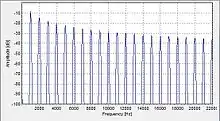
In realen Systemen tritt durch die Bandbegrenzung nur eine endliche Anzahl von Summanden auf. Die Summe der harmonischen Schwingungen resultiert dann in einen verzerrten Sägezahnverlauf. Dieser Effekt ist in nebenstehender Abbildung mit nur einer endlichen Anzahl von Sinusschwingungen grafisch verdeutlicht.

Im Bereich der diskreten Signalverarbeitung ist es ausreichend, die Anzahl der zu bestimmenden Oberschwingungen auf die halbe Abtastrate zu limitieren.

Anwendungen

Eine Besonderheit dieser Schwingungsform ist, dass sie theoretisch alle ganzzahligen Vielfachen einer Grundfrequenz in den Oberschwingungen enthält, die man Harmonische nennt. Das große Spektrum hat allgemein Vorteile bei der Anwendung in elektronischen Musikinstrumenten wie vor allem der elektronischen Orgel mit subtraktiver Klangsynthese. Durch Filterung der Sägezahnschwingung können aus einer einzelnen generierten Schwingung verschiedene Obertöne bevorzugt werden, wie sie für die Klangfarben der Orgel benötigt werden, z. B. eher Richtung Trompeten- oder Flötenklang. Typische Kippschwingungen werden u. a. auch bei Streichinstrumenten erzeugt.

Daneben wird die Kippschwingung in Oszillographen zur horizontalen Ablenkung des Elektronenstrahls benutzt. In Kathodenstrahlröhrenbildschirmen (beispielsweise in herkömmlichen Röhrenfernsehern) wird der Elektronenstrahl sowohl in horizontaler, als auch in vertikaler Richtung mit einer Kippschwingung angesteuert, wobei die Frequenz der horizontalen Ablenkung in der Regel die deutlich höhere ist.

Realisierungsbeispiele

Ein einfaches Beispiel für eine Kippschwingung ist ein drehbar oberhalb seines Schwerpunktes im Leerzustand aufgehängter, konischer Behälter (Eimer), der allmählich mit Wasser befüllt wird. Erreicht der Inhalt die Höhe, bei der der Schwerpunkt oberhalb des Drehpunktes liegt, kippt der Behälter und das Wasser läuft aus.

Eine weitere Anwendung ist der Widder, eine einfache Wasserpumpe.

In der Elektronik können Kippschwingungen mit Hilfe einer Glimmlampe oder durch komplexere Schaltungen wie Sperrschwinger, Miller-Transitron, Sägezahn-Generator oder Kippschwinger erzeugt werden.

Siehe auch

Literatur

Curt Rint (Hrsg.): Handbuch für Hochfrequenz- und Elektro-Techniker. Band 2. 13., durchgesehene Auflage. Hüthig und Pflaum, Heidelberg u. a. 1981, ISBN 3-778-50699-4.
Gregor Häberle, Heinz Häberle, Thomas Kleiber: Fachkunde Radio-, Fernseh- und Funkelektronik. 3., neubearbeitete und erweiterte Auflage. Verlag Europa-Lehrmittel, Haan-Gruiten 1996, ISBN 3-8085-3263-7.
Helmuth Wilhelms, Dieter Blank, Hans Mohn: Nachrichtentechnik (= Elektro-Fachkunde. Bd. 3). Teubner, Stuttgart 1982, ISBN 3-519-06807-9.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.