Stimmung (Musik)

Unter Stimmung versteht man in der Musik die Festlegung der Tonhöhen (Frequenzen) von Schallquellen, insbesondere von Musikinstrumenten. In der Praxis genügt hierzu oft (etwa bei einigen Blasinstrumenten) die Festlegung der absoluten Tonhöhe durch Abgleich mit einer vorgegebenen Frequenz (z. B. dem Kammerton a¹ = 440 Hz). Vor allem bei Saiten- und Tasteninstrumenten müssen außerdem die Frequenzverhältnisse der Saiten oder der einzelnen Töne untereinander eingestellt werden.

Die meisten Streichinstrumente, etwa die Violine, können innerhalb eines weiten Bereichs grundsätzlich jede beliebige Tonhöhe erzeugen, insbesondere z. B. jedes Intervall rein spielen. (Eine reine Stimmung beruht auf dem Tonmaterial der Obertonreihe). Dagegen werden bei Tasteninstrumenten zwölf Halbtöne pro Oktave im Allgemeinen fest eingestimmt. Eine in allen Tonarten zugleich reine Stimmung mit nur zwölf Tonstufen gibt es nicht; daher müssen Kompromisse eingegangen werden (siehe Temperierte Stimmung, Wohltemperierte Stimmung, Reine Stimmung bei Tasteninstrumenten).

Viele Blasinstrumente können nicht alle verwendbaren Tonstufen (üblicherweise zwölf) innerhalb der Oktave gleichmäßig leicht und rein erzeugen, sondern haben bevorzugte diatonische Tonleitern. Auch dies wird meist einfach als die „Stimmung“ des Instruments bezeichnet, bei Blechblasinstrumenten manchmal genauer als Grundstimmung. Unabhängig davon ist der oben genannte Abgleich der absoluten Tonhöhe auf einen Stimmton, z. B. den Kammerton, für das Zusammenspiel mit anderen Instrumenten außerdem nötig.

Kammerton

Eine Angabe wie „Stimmung 440 Hz“ nennt die Frequenz eines bestimmten Stimmtons, üblicherweise des a’ (eingestrichenes a, auch Kammerton genannt). Heutige Instrumente werden beispielsweise auf a¹ = 440 oder 442 Hz gestimmt. Um 1900 herum war 435 Hz üblich. In früheren Jahrhunderten waren, lokal abhängig, verschiedenste Stimmhöhen, auch deutlich höhere als 440 Hz, gebräuchlich (→ Cornettton). Heute wird bei historischen Instrumenten häufig ein Kammerton von 415 Hz verwendet, der ziemlich genau einen Halbton tiefer als 440 Hz ist (→ Chorton).

Grundtonleiter und transponierende Instrumente

Mit der Stimmung eines Instruments ist manchmal seine Grundtonleiter oder deren Grundton gemeint, wie zum Beispiel F-Dur bzw. der Ton f¹ bei der Altblockflöte; siehe Holzblasinstrument.

Manchmal ist mit der Stimmung eines Instruments der Ton gemeint, der bei Verwendung von speziell für dieses Instrument geschriebenen Noten an Stelle eines geschriebenen C erklingt (siehe Transponierendes Musikinstrument). Dieses ist bei manchen Instrumenten, z. B. der Trompete, zugleich der Grundton (siehe oben), bei anderen aber nicht; z. B. ist bei der „in B gestimmten“ Klarinette eher F-Dur als Grundtonleiter anzusehen.

Mit „C-Stimmung“ kann dementsprechend gemeint sein, dass für das betreffende Instrument Noten in wirklicher Tonhöhe üblich sind.

Stimmungssysteme

Ein Stimmungssystem ist die Art, wie bei einem Instrument die genauen Frequenzverhältnisse der spielbaren Töne innerhalb einer Oktave, also in den meisten Fällen die zwölf Halbtonschritte des gewählten Tonsystems gestimmt sind. Eine andere Bezeichnung dafür (insbesondere bei Tasteninstrumenten) ist Temperatur oder Temperierung. Die Stimmungssysteme machen nur Aussagen über die Frequenzverhältnisse der einzelnen Töne zueinander. Es wird keine Aussage über die absolute Tonhöhe bzw. die Frequenz selbst gemacht. Die absolute Tonhöhe wird durch die Angabe der Frequenz des Anfangstons oder des Tons a¹ festgelegt.

Frequenzverhältnisse im Tonsystem

Jeder Ton hat in jeder Tonleiter eine andere Bedeutung, z. B. ist das E in der E-Dur-Tonleiter der Grundton, in der C-Dur-Tonleiter der dritte Ton (die Terz) und in der A-Dur- oder a-Moll-Tonleiter der fünfte Ton (die Quinte). Für jede der möglichen Positionen im Tonleiterraum ergeben sich unterschiedliche Frequenzverhältnisse der Töne zueinander, die aber untereinander angeglichen werden müssen, um auf einem Instrument in verschiedenen Tonarten gespielt werden zu können. Eine Folge von reinen großen Terzen (Frequenzverhältnis 5:4) ist stimmtechnisch nicht in Übereinstimmung zu bringen mit einer Folge von reinen Quinten (Frequenzverhältnis 3:2). Bei der üblichen Beschränkung auf zwölf Tonstufen pro Oktave bedeutet dies, dass man Kompromisse eingehen muss: Je reiner eine bestimmte Tonart gestimmt wird, umso unreiner klingen andere Tonarten.

Besonders auffällig wird dieses Problem bei der Mehrstimmigkeit.

Überblick über die Stimmungssysteme

Es gibt eine Vielzahl von Systemen, die Töne des Tonsystems für eine 12-stufige Tastatur einzustimmen. Die wichtigsten Stimmungssysteme sind:

Pythagoreische Stimmung (alle Quinten außer einer Wolfsquinte sind rein, Terzen sind dissonant)
Reine Stimmung oder Natürlich-harmonische Stimmung (In allen Tonarten reine Terzen und Quinten)
Mitteltönige Stimmungen (Möglichst reine Terzen, nur in wenigen Tonarten möglich.)
- die 1/4-Komma mitteltönige Stimmung (die Basistonarten B-, F-, C-, G-, D-, A-, E-Dur enthalten reine Terzen.)
- Silbermann-Sorge-Temperatur (sie kann als 1/6-Komma mitteltönige Stimmung bezeichnet werden)
Wohltemperierte (Temperierte) Stimmung (alle Tonarten sind akzeptabel spielbar)
- Werckmeister-Stimmung
- Kirnberger-Stimmung
- Vallotti-Stimmung
- Neidhardt-Temperatur
Gleichstufige Stimmung (Die Oktave ist in 12 gleiche Halbtöne geteilt)

Die Wahl der Stimmung ist davon abhängig, welche Musik gespielt werden soll. Die heute überwiegend verwendete Gleichstufige Stimmung ist für Musik nach 1800 geeignet. Frühere Musik oder außereuropäische Musik (Weltmusik) lebt sehr stark von der Intonationsreinheit oder von verschiedenartigen Tonartcharakteren. Diese Forderungen können durch die Gleichstufige Stimmung nicht bedient werden. Im Rahmen der Historischen Aufführungspraxis Alter Musik werden daher ältere Stimmungssysteme wieder verstärkt erforscht, um adäquate Wiedergaben zu ermöglichen.

Antike

Pythagoras mit verschiedenen in Quinten gestimmten Instrumenten (eingezeichnete Intervallverhältnisse 16:12:9:8:6:4).
Aus: Franchino Gaffurio: Theorica musicae, 1492 (1480?)

Die erste theoretische Beschreibung eines Stimmungssystems wurde in der Antike entsprechend der Legende von Pythagoras in der Schmiede Pythagoras von Samos zugeschrieben. Pythagoras war ein nach Unteritalien ausgewanderter Philosoph und Mathematiker. Er war der Auffassung, dass der gesamte Kosmos nach bestimmten Zahlenverhältnissen geordnet sei und die Musik Abbild der kosmischen Ordnung sei.

Der antiken Überlieferung zufolge, deren Glaubwürdigkeit allerdings in der modernen Forschung umstritten ist, untersuchte Pythagoras auf dem Monochord die Intervalle zwischen Saitenteilen mit ganzzahligen Längenverhältnissen. Beispielsweise klingt eine Saite, wenn sie in der Hälfte geteilt wird, eine Oktave höher als in ihrer vollen Länge; das zugehörige Zahlenverhältnis ist also 1:2. Er beschrieb so erstmals die natürlichen Intervalle, die aus der Obertonreihe bekannt sind.

Pythagoras soll eine siebentönige Skala auf der Grundlage der reinen Quinte (mit dem nach der Oktave einfachsten Zahlenverhältnis 2:3) eingeführt haben. Die Töne werden dabei von einem Anfangston ausgehend durch Quintschritte ermittelt und in eine gemeinsame Oktave transponiert. Das Ergebnis ist die Pythagoreische Stimmung, mit der sich später auch die Musiktheorie des Euklid beschäftigt. Von Euklid stammt auch die erste genaue Berechnung der Frequenzproportion des pythagoreischen Kommas.

Im 1. Jahrhundert v. Chr. führte der Musiktheoretiker Didymos die „Naturterz“ (Frequenzverhältnis 5:4) in sein enharmonisches Tongeschlecht ein.

Eine andere Tradition geht auf Aristoxenos zurück, der die Ungenauigkeiten älterer Untersuchungen mit dem Monochord herausstellte und eine alternative Tonskalenberechnung begründete.

Mittelalter

Das Tonsystem des Pythagoras wurde von den Römern und im mittelalterlichen Europa übernommen. Monochorde, Glocken (vgl. Abbildung) und Orgelpfeifen wurden pythagoreisch gestimmt und in der gregorianischen Musizierpraxis verwandt. Die Harmonik der frühen Mehrstimmigkeit bevorzugte die in der pythagoreischen Stimmung tatsächlich reinen Intervalle (die Komplementärintervalle Quinte und Quarte sowie Prime und Oktave).

Renaissance

In der Renaissance gab es vor allem zwei für das Tonsystem wichtige Entwicklungen:

Die zunehmende Chromatik in der Vokalpolyphonie erweiterte den Tonvorrat endgültig auf zwölf Töne.
Das Dissonanzempfinden veränderte sich. Die Terz, im Mittelalter noch als dissonant eingestuft, wurde zum Harmonieträger im entstehenden Dur-Moll-System. Unterstützt wurde dieses Dissonanzempfinden allerdings dadurch, dass die Terz in der im Mittelalter verwendeten pythagoreischen Stimmung (Frequenzverhältnis 81:64) auch aus heutiger Sicht dissonant klingt; die reine große Terz (Frequenzverhältnis 5:4) kam erst mit dem Wechsel zur reinen Stimmung in das System.

Die neue Orientierung an der Terz und der Bedarf einer chromatischen Tonleiter führte zu Problemen mit der quintbasierten pythagoreischen oder auch der reinen Stimmung:

Zwölf aufeinander geschichtete Quinten ergeben keinen geschlossenen Quintenzirkel. Der 13. Ton ist um das pythagoreische Komma höher als der Ausgangston. (Physikalisch ist er 7 Oktaven plus das pythagoreische Komma höher; bei der musikalischen Betrachtung von Tonleitern und Intervallen werden aber Töne im Abstand von Oktaven als gleichwertig angesehen.)
Vier aufeinander geschichtete Quinten (z. B. C — G — D — A — E) ergeben keine reine große Terz. Der fünfte Ton ist um das syntonische Komma höher als eine reine große Terz auf dem Ausgangston.

Man wählte, dem neuen Klangideal entsprechend, die reine große Terz (mit dem nach Quinte und Quarte nächsteinfacheren Frequenzverhältnis 5:4) als neues Stammintervall und entwickelte, da die reine Stimmung auf den üblichen Tasteninstrumenten nicht verwirklicht werden konnte, die sogenannte mitteltönige Stimmung. Dabei führte man, um dem syntonischen Komma aus dem Weg zu gehen, leicht verkleinerte Quinten ein, von denen vier aufeinandergeschichtet eine reine große Terz bilden.

Durch die Folge von elf mitteltönigen Quinten

Es — B — F — C — G — D — A — E — H — Fis — Cis — Gis

erhielt man die zwölf Töne unseres abendländischen Tonsystems.

So erhielt man acht große Terzen wie gewünscht rein. (z. B. C — E durch vier mitteltönige Quinten C — G — D — A — E); vier Terzen mussten unrein bleiben (z. B. H-Dis, da Dis als Es eingestimmt ist und Dis deshalb nicht vier mitteltönige Quinten über H liegt, sondern acht mitteltönige Quinten unter H; vgl. obige Quintfolge).

Die mitteltönige Stimmung war jedoch auch ein Kompromiss und in mancher Hinsicht nicht zufriedenstellend. Theorie und Praxis:

Durch dieses System entstanden viele Intervalle, die sich nicht durch ganzzahlige Brüche ausdrücken lassen, was einen Widerspruch zur pythagoreischen Auffassung der Musik darstellte. Die Ursache dafür sind die zugunsten der Terzreinheit eingeführten mitteltönigen Quinten, für die ein Saitenlängenverhältnis von $1:{\sqrt[{4}]{5}}$ gilt, das keine rationale Zahl ist.
Zwölf aufeinandergeschichtete mitteltönige Quinten ergeben einen Ton, der um die so genannte kleine Diësis tiefer ist als der Ausgangston (vgl. Problematik der pythagoreischen Stimmung).
Die Quinte As — Es bzw. Gis — Dis ist um die kleine Diesis zu groß, da das As „alias Gis“ nicht als mitteltönige Quinte unter Es gestimmt wird, sondern elf mitteltönige Quinten über Es liegt (vgl. obige Quintfolge). Diese so genannte Wolfsquinte klingt sehr unrein. In der mitteltönigen Stimmung klingen daher Tonarten, die diese Quinte enthalten (z. B. Es-Dur oder Cis-Dur), extrem dissonant und sind allenthalben zur Darstellung bestimmter Affekte brauchbar.

Dennoch setzte sich die mitteltönige Stimmung durch. Modulatorische Entwicklung, wie sie später üblich wurde, war in der Renaissance wenig gebräuchlich. Man kam deshalb zunächst mit dem gut klingenden Tonartenbereich aus. Um auch weitere Tonarten in der mitteltönigen Stimmung spielbar zu machen, wurden Tasteninstrumente mit z. B. 31 Tönen in der Oktave gebaut, die sich aber nicht durchsetzen konnten.

Barock

Im Laufe des 17. Jahrhunderts wurde diese Beschränkung auf zentrale Tonarten zunehmend als störend empfunden. Um in der Wahl der Tonarten freier zu werden, begann man, Stimmungssysteme zu entwickeln, in denen alle Tonarten spielbar sind, wenn auch nicht alle in gleicher Qualität. Dafür mussten Abstriche in der Reinheit der Terzen hingenommen werden. Diese Stimmungen wurden „Wohltemperierte Stimmungen“ oder „Gute Temperaturen“ genannt, im Gegensatz zur nun als „schlecht“ empfundenen mitteltönigen Stimmung. Beispiele hierfür sind die Stimmungen von Andreas Werckmeister Werckmeister III-VI, () oder die Stimmungen des Orgelbauers Gottfried Silbermann.

Allerdings gab es keine Temperatur, die sich universell durchsetzte wie vormals die mitteltönige Stimmung (die mit den neuen Temperaturansätzen übrigens nicht einfach verschwand). Am Beispiel Werckmeisters kann man sehen, dass zunächst auch nicht unbedingt angestrebt wurde, eine einheitliche Stimmung zu etablieren. Er beschreibt in seinem wichtigsten Werk Musicalische Temperatur verschiedene Temperaturen, die je nach Bedürfnis mehr oder weniger geeignet sein können.

Grundsätzlich kann man (bei Werckmeister und anderen) zwei Ansätze unterscheiden:

Einige Systeme strebten danach, die Tonarten mit wenigen Vorzeichen möglichst klar klingen zu lassen, aber auch diejenigen mit vielen Vorzeichen, wenn auch mit getrübterem Klang, spielbar zu machen. (Beispiel: Die Werckmeister-II-Temperatur.)
Andere Systeme versuchten, alle Tonarten möglichst gut spielbar zu machen. (Beispiel: Die Werckmeister-III-Temperatur). Dieser Ansatz führte am Ende der Entwicklung zur heute gebräuchlichen gleichstufigen Temperatur. Bei diesem Ansatz muss man allerdings einen – im Gegensatz zu den zentralen Tonarten im oben beschriebenen Ansatz – relativ matten Klang aller Tonarten in Kauf nehmen.

Gleichstufige Temperatur

Siehe auch Hauptartikel: Gleichstufige Stimmung

Bereits in der Renaissance suchte man nach Methoden, die Laute gleichstufig zu stimmen. Da es nicht möglich ist, auf Bundinstrumenten jeden Ton einzeln einzustimmen, kommt es zu Problemen. (Weil z. B. in der mitteltönigen Stimmung nicht alle großen Terzen gleich sind, müsste auf der A-Saite der vierte Bund die Saite für die große Terz Cis auf ⁴⁄₅ der Länge verkürzen, auf der H-Saite soll Dis „alias“ Es jedoch nicht als große Terz eingestimmt werden. Die Saite müsste hier in der mitteltönigen Stimmung auf ²⁵⁄₃₂ der Länge verkürzt werden.)

Da die Möglichkeiten der Wurzelrechnung zu dieser Zeit noch beschränkt waren, konnte man den gleichstufigen Halbton mit dem Verhältnis $1:{\sqrt[{12}]{2}}$ noch nicht berechnen. Dennoch konnte man ein gleichstufiges Griffbrett bauen, da man geometrische Methoden zur nähungsweisen Konstruktion einfacher Wurzelverhältnisse zur Hand hatte. Der venezianische Musiker und Musiktheoretiker Gioseffo Zarlino beschreibt schon 1558 eine solche Methode.

Der Lautenist Vincenzo Galilei, Vater des Galileo Galilei, gab die einfachen ganzzahligen Verhältnisse dennoch nicht auf. Er verkürzte die Saite pro Bund auf ¹⁷⁄₁₈ der Länge. In der Theorie kommt er dabei mit dem zwölften Halbton zwar nicht ganz bei der Oktave an, in der Praxis ist das Ergebnis aber recht brauchbar, da der Ton durch das Drücken und den dabei überwunden Abstand von Bund und Saite (die Saite wird länger) und durch den Fingerdruck auf die Saite (Saitenspannung erhöht sich) noch ein wenig erhöht wird. Die Saitenlänge kann auch nach der Konstruktion des Griffbretts durch die Umpositionierung des Stegs noch minimal korrigiert werden, so dass das Ergebnis noch besser wird.

Mathematiker und Musiktheoretiker versuchten sich in den folgenden knapp 200 Jahren daran, mit unterschiedlichen Methoden genauere Zahlenwerte für die gleichstufige Temperatur zu ermitteln. Im 19. Jahrhundert setzte sich die gleichstufige Temperatur schließlich allgemein durch.

Heute gibt es wieder Diskussionen darüber, wie beispielsweise Orgeln gestimmt werden sollten. Viele historische Kompositionen gehen von unterschiedlichen Klangeigenschaften verschiedener Tonarten und Akkorde aus, die auf gleichstufig gestimmten Instrumenten nicht reproduzierbar sind. Dies ist insbesondere für die Historische Aufführungspraxis von Bedeutung.

Vergleich der Stimmungssysteme

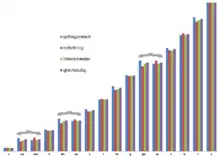
Grafischer Vergleich der pythagoreischen und mitteltönigen Stimmung mit der wohltemperierten Stimmung nach Werckmeister (III) und der gleichstufigen Stimmung. In vertikaler Richtung sind die jeweiligen Tonhöhen der Grundtöne angegeben.
Die vier pythagoreischen Töne C, F, G und C sind in allen Stimmsystemen praktisch identisch. Bei den Leittönen nach oben (Cis, Dis, E, Fis, Gis und H) ist die pythagoreische Stimmung immer hoch und die mitteltönige Stimmung immer tief; bei den Leittönen nach unten (Des, Es, As und B) ist die pythagoreische Stimmung immer tief und die mitteltönige Stimmung immer hoch. Die Werckmeister-Stimmung gleicht die Differenzen aus und nähert sich der gleichstufigen Stimmung an.

Hinweis: Reine Intervalle sind durch einfache ganzzahlige Frequenzverhältnisse charakterisiert, temperierte Intervalle haben auch irrationale Frequenzverhältnisse. Deshalb erfolgt der Größenvergleich hier mit der Einheit Cent, wobei 1 Oktave = 1200 Cent.

Die folgende Tabelle gibt die Höhe der Tonstufen einer Dur-Tonleiter verschiedener Stimmungen in Cent (gerundet) an:

Name	Prime	große Sekunde	große Terz	Quarte	Quinte	große Sexte	große Septime	Oktave
Reine Stimmung	0	204/182	386	498	702	884	1088	1200
Pythagoreische Stimmung	0	204	408	498	702	906	1110	1200
1/4-Komma-mitteltönige Stimmung	0	193	386	503	697	890	1083	1200
Gleichstufige Stimmung	0	200	400	500	700	900	1100	1200

Bemerkung: Bei der reinen Stimmung gibt es den großen Ganzton (In C-Dur zum Beispiel C-D) mit 204 Cent und den kleinen Ganzton (in C-Dur zum Beispiel D-E) mit 182 Cent. Beides wird als große Sekunde bezeichnet. In der mitteltönigen Stimmung werden die beiden Ganztöne gemittelt zu je 193 Cent. Zusammen ergeben sie die reine Terz mit 386 Cent.

Anhand der folgenden Tabellen lässt sich abschätzen, wie weit welche Quinten und Terzen in verschiedenen Stimmungen von den reinen Intervallen abweichen. Daran kann man ermessen, wie stark „verstimmt“ entsprechende Dur-Akkorde in den verschiedenen Tonarten erklingen. (Die fett markierten Zahlen zeigen die Wolfsquinte oder analog die Wolfsterz; auffällig: die vier fast reinen Terzen in der pythagoreischen Stimmung.)

Quinten in Cent	C–G	Des–As Cis–Gis	D–A	Es–A Dis–Ais	E-H	F–C	Fis–Cis Ges–Des	G–D	As–Es Gis–Dis	A–E	B–F	H–Fis	C–G
1/4-Komma-mitteltönige Stimmung	697	697	697	697	697	697	697	697	738	697	697	697	697
Werckmeister III-wohltemperiert	696	702	696	702	702	703	702	696	702	702	702	696	696
gleichstufige Stimmung	700	700	700	700	700	700	700	700	700	700	700	700	700
pythagoreische Stimmung	702	702	702	702	702	702	702	702	679	702	702	702	702

Zum Vergleich: reine = pythagoreische Quinte = 702 Cent, gleichstufige Quinte = 700 Cent, 1/4-Komma-mitteltönige Quinte = 697 Cent.

Große Terz in Cent	C-E	Des–F Cis–Eis	D–Fis	Es–G	E–Gis	F–A	Fis–Ais Ges–B	G–H	As–C Gis–His	A–Cis	B–D	H–Dis Ces–Es	C–E
1/4-Komma-mitteltönige Stimmung	386	427	386	386	386	386	427	386	427	386	386	427	386
Werckmeister III-wohltemperiert	390	408	396	402	402	391	408	396	408	402	397	402	390
gleichstufige Stimmung	400	400	400	400	400	400	400	400	400	400	400	400	400
pythagoreische Stimmung	408	384	408	408	408	408	384	408	384	408	408	384	408

Zum Vergleich: reine = 1/4-Komma-mitteltönige große Terz = 386 Cent, gleichstufige große Terz = 400 Cent, pythagoreische große Terz = 408 Cent.

Ein unmittelbarer akustischer Vergleich der vorstehend genannten und weiterer Stimmungen ist mit geeigneter Software wie z. B. GrandOrgue, Hauptwerk oder an entsprechend disponierten Keyboards[1] mit deren "Presets" oder durch sogenanntes "user scale tuning"[2] möglich. Für den Einsatz am realen Instrument gibt es Stimmgeräte mit vorprogrammierten historischen Stimmungen.

Stimmen von Instrumenten

Als Stimmen von Instrumenten bezeichnet man die Einstellung der Tonhöhe. Ein Blasinstrument wird als Ganzes gestimmt, bei Saiteninstrumenten (Streichinstrumente, Gitarre, Harfe) jede Saite einzeln. Bei Klavieren und Orgeln sind sogar für jeden einzelnen Ton mehrere Saiten bzw. Pfeifen zu stimmen. Einige Instrumente werden sogar in „Lagen“ gestimmt; dazu gehört zum Beispiel das Einstellen der Oktavreinheit bei Gitarren.

Die meisten Instrumente lassen sich innerhalb gewisser baulich vorgegebener Grenzen stimmen, aber es gibt auch Instrumente, die aufgrund ihrer Bauweise nicht oder nur sehr aufwendig stimmbar sind. Hierzu zählen vor allem Instrumente aus dem Bereich Perkussion und der Idiophone, z. B. Glockenspiele.

Beim Stimmen von Instrumenten kann man drei Aufgaben unterscheiden:

die Stimmung eines Instruments „in sich“ (wichtig bei den Tasten- und Saiteninstrumenten)
die Abstimmung mehrerer Instrumente miteinander
die Stimmung eines Instruments auf absolute Tonhöhen

Der manuelle Vorgang des Stimmens ist von Instrument zu Instrument verschieden. Bei Blasinstrumenten erfolgt dieses meistens durch Veränderung der Rohrlänge, bei Streichinstrumenten durch die Veränderung der Saitenspannung. Bei Tasteninstrumenten muss meistens jeder einzelne Ton gestimmt werden. Die Stimmung eines Ensembles erfolgt in der Regel nach dem unflexibelsten Instrument, meistens sind das die Tasteninstrumente. Im Orchester gibt die Oboe aufgrund ihres obertonreichen Klangs das a’ als Kammerton vor. Steht kein Referenzinstrument zur Verfügung, kann eine Stimmgabel, eine Stimmpfeife oder ein elektronisches Stimmgerät als Hilfe genutzt werden. Elektronische Musikinstrumente müssen aufgrund der verwendeten Tonerzeugung „in sich“ nicht gestimmt werden, oftmals können sie aber insgesamt in kleinen bis hin zu transponierenden Abstufungen verändert werden.

Durch die Häufigkeit des Stimmvorganges haben viele routinierte Instrumentalisten eine Art Absolutes Gehör für ihre Stimmtöne (Grundtöne bei Bläsern, Leersaiten bei Streichern) entwickelt.

Siehe auch

Literatur

Ernst Kochsiek: Konzertstimmungen. Erlebnisse und Begegnungen mit berühmten Pianisten. Mit Audio-CD. Edition Bochinsky, 2001, ISBN 978-3-923639-46-5
Klaus Lang: Auf Wohlklangswellen durch der Töne Meer – Temperaturen und Stimmungen zwischen dem 11. und 19. Jahrhundert, herausgegeben von Robert Höldrich, Institut für Elektronische Musik (IEM) an der Universität für Musik und darstellende Kunst in Graz (1990), PDF-Version
Gottfried Rehm: Einführung in alte Stimmungssysteme. In: Gitarre & Laute 4, 1982, 1, S. 12–14.

Stimmungen in Musikgeschichte und -praxis

Weblinks

Commons: Musical tuning – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Stimmung – Lern- und Lehrmaterialien

Einzelnachweise

z. B. Roland Classic C-200 oder Yamaha P-155 oder Korg X-50
http://www.farago.info/hobby/stimmungen/Tuning.htm Musikalische Stimmungen gestern und heute

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] z. B. Roland Classic C-200 oder Yamaha P-155 oder Korg X-50

[2] ttp://www.farago.info/hobby/stimmungen/Tuning.htm Musikalische Stimmungen gestern und heute