Kurzzeit-Fourier-Transformation

Die Kurzzeit-Fourier-Transformation (englisch short-time Fourier transform, kurz STFT) ist eine Methode aus der Fourier-Analysis, um die zeitliche Änderung des Frequenzspektrums eines Signals darzustellen. Während die Fourier-Transformation keine Informationen über die zeitliche Veränderung des Spektrums bereitstellt, ist die STFT auch für solche Signale geeignet, deren Frequenzeigenschaften sich im Laufe der Zeit verändern. Anwendung findet die STFT unter anderem in Messgeräten wie den Spektrumanalysatoren.

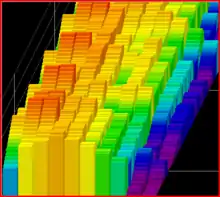
STFT eines Audiosignals welches über die Frequenz (horizontale Achse) und die Zeit (Achse in Bildebene hinein) dargestellt ist. Die Intensität ist durch die Höhe und Farben der einzelnen Balken dargestellt

Zur Transformation wird das Zeitsignal in einzelnen Zeitabschnitte mit Hilfe einer Fensterfunktion unterteilt und diese einzelnen Zeitabschnitte in jeweils einzelne Spektralbereiche überführt. Die zeitliche Aneinanderreihung der so gewonnenen Spektralbereiche stellt die STFT dar, welche sich dreidimensional oder in Flächendarstellung mit verschiedenen Farben grafisch darstellen lässt.

Eine spezielle Variante der STFT ist die Gabor-Transformation.

Frequenz- und Zeitauflösung

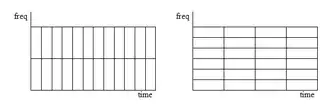
Grafische Darstellung der Zeit-Frequenz-Auflösung. Bei gleichem Flächeninhalt der einzelnen Rechtecke, dies entspricht grafisch der Küpfmüllerschen Unbestimmtheitsrelation, weist das linke Diagramm eine höhere Zeitauflösung auf, das rechte Diagramm eine bessere Frequenzauflösung

Eine wesentliche Eigenschaft der Kurzzeit-Fourier-Transformation stellt die Küpfmüllersche Unbestimmtheitsrelation dar. Diese Relation beschreibt einen Zusammenhang zwischen der Auflösung im Zeitbereich und der Auflösung im Frequenzbereich, wobei das Produkt aus Zeit und Frequenz einen konstanten Wert darstellt. Wird eine möglichst hohe Auflösung im Zeitbereich gewünscht, um beispielsweise den Zeitpunkt, wann ein bestimmtes Signal ein- oder aussetzt, zu ermitteln, dann folgt daraus eine unscharfe Auflösung im Frequenzbereich. Ist eine hohe Auflösung im Frequenzbereich nötig, um die Frequenz genau bestimmen zu können, dann folgt daraus eine Unschärfe im Zeitbereich, das heißt die genauen Zeitpunkte können nur unscharf festgestellt werden.

Folgendes Beispiel mit vier verschiedenen Einstellungen soll den Zusammenhang der Küpfmüllerschen Unbestimmtheitsrelation mit Bezug zur Kurzzeit-Fourier-Transformation darstellen. Dabei wird in allen vier Fällen ein harmonisches Testsignal mit 20 Sekunden Dauer und einer Abtastfrequenz von 400 Hz genommen und zum Startzeitpunkt bei 0 Sekunden, nach 5 Sekunden, 10 Sekunden und bei 15 Sekunden die Frequenz zwischen anfangs 10 Hz, 25 Hz, 50 und abschließend 100 Hz sprunghaft geändert. In jeder der nachfolgenden vier Darstellungen wurde, bei sonst identischem Testsignal, das Zeitfenster für die Fensterfunktion der Kurzzeit-Fourier-Transformation zwischen 25 ms, 125 ms, 375 ms und 1 s verändert, die spektrale Intensität ist in den Diagrammen farblich abgebildet:

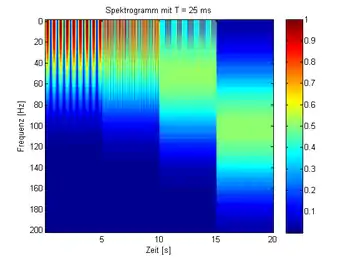Fensterbreite 25 ms	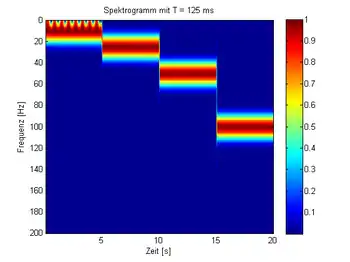Fensterbreite 125 ms
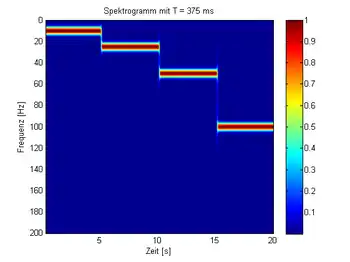Fensterbreite 375 ms	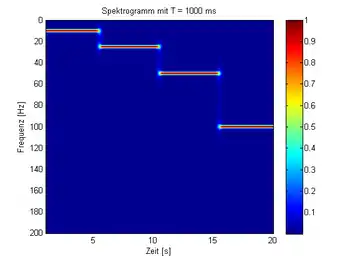Fensterbreite 1 s

Bei der ersten Darstellung mit einer Fensterfunktion von 25 ms Dauer ist eine starke „Verschmierung“ im Spektrum zu erkennen, die genauen Frequenzen lassen sich kaum ermitteln. Dafür ist bei dieser Fensterbreite die Zeitauflösung sehr hoch und die Umschaltzeitpunkte von einer Frequenz zur nächsten lassen sich genau bestimmen. Die intermittierende und über einen breiten Frequenzbereich verschmierte Darstellung der Intensität, vor allem bei der niedrigen Frequenz von 25 Hz erkennbar, ist durch den Leck-Effekt bedingt.

In der letzten Darstellung mit einer Fensterbreite von 1 s ist die Frequenzauflösung am höchsten – es lassen sich mit den schmalen waagrechten Linien die Frequenzen sehr genau bestimmen. Dafür ist der genaue Umschaltzeitpunkt zwischen den einzelnen Frequenzen nur unscharf und in der Darstellung durch einen hellblauen Fleck am Ende der Linien erkennbar.

Arten

Bei der Kurzzeit-Fourier-Transformation wird zwischen einer zeitkontinuierlichen Transformation und einer in der digitalen Signalverarbeitung angewendeten zeitdiskreten Transformation unterschieden.

Zeitkontinuierliche STFT

Das kontinuierliche Zeitsignal wird mit einer Fensterfunktion $w\!$ multipliziert, die nur für den gewählten Zeitabschnitt Werte ungleich 0 aufweist. Übliche Fensterfunktionen sind neben der Rechteckfunktion das Von-Hann-Fenster und das Gauß-Fenster. Außerhalb des Fensters liefert die Fensterfunktion den Wert 0, womit auch das Produkt $x(\cdot )w(\cdot )$ verschwindet. Die zeitkontinuierliche STFT ist gegeben als:

X(\tau ,\omega )=\int _{-\infty }^{\infty }x(t)w(t-\tau )\mathrm {e} ^{-\mathrm {j} \omega t}\,\mathrm {d} t

mit der Kreisfrequenz $\omega$ .

Zeitdiskrete STFT

Das zeitdiskrete Signal liegt als eine Signalfolge einzelner Abtastwerte vor, die durch eine diskrete Fensterfunktion in einzelne Abschnitte unterteilt wird. Die Zeitachse wird durch einen im Allgemeinen ganzzahlig gewählten Index $n$ ausgedrückt. Die diskrete STFT ist gegeben als

X(m,\omega )=\sum _{n=-\infty }^{\infty }x[n]w[n-m]\mathrm {e} ^{-\mathrm {j} \omega n}

.

In den Anwendungen wird die Berechnung der Transformation durch eine Schnelle Fourier-Transformation (FFT) realisiert.

Literatur

Uwe Kiencke, Michael Schwarz, Thomas Weickert: Signalverarbeitung - Zeit-Frequenz-Analyse und Schätzverfahren. Oldenbourg, München 2008, ISBN 978-3-486-58668-8.

Weblinks

Short-Time Fourier Transformation (STFT) with Matlab Implementation

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.