Tonhöhe

Die Tonhöhe wird in der Praxis mit der Frequenz (Schwingungsanzahl pro Zeitspanne) eines hörbaren Tones gleichgesetzt, genauer: mit der Grundfrequenz, also der Frequenz des tiefsten Teiltons in dem betreffenden Klang (siehe z. B. Stimmung (Musik), Intervall (Musik), Kammerton). Die Tonhöhe ist neben der Tondauer, der Lautheit und der Klangfarbe eine wichtige Eigenschaft musikalischer Töne und der Vokale gesprochener Sprache.[1]

Definition

Das American National Standards Institute[2] definiert die Tonhöhe als eine Eigenschaft der auditorischen Empfindung „nach der Klänge auf einer musikalischen Tonleiter geordnet werden können (ANSI S1.1)“.[3] Dabei werden Tonhöhen im Sinne einer musikalischen Melodie als höher oder tiefer wahrgenommen[4], was jedoch voraussetzt, dass der Hörschall bezüglich Frequenz und Klarheit stabil genug ist, um ihn von einem Geräusch zu unterscheiden.[5] Bei künstlich erzeugten reinen Tönen (Sinuston, monofrequenter Schall) korreliert die Tonhöhe mit der Frequenz des Tones. Normalerweise wird die Tonhöhe einfach als die Grundfrequenz eines periodischen Schalls verstanden;[6] aber besonders in der Musik beeinflussen auch harmonische und melodische Zusammenhänge die Wahrnehmung.[7]

Hörschall, dem das menschliche Gehör eine Tonhöhenempfindung zuordnen kann, nennt man tonal. Einen tonalen Charakter haben Schallsignale, bei denen sich die Zeitstruktur periodisch wiederholt (z. B. Klang von schwingenden Saiten). Einen tonalen Charakter haben aber auch nicht-periodische Schallsignale, bei denen eng umgrenzte Frequenzbereiche hervorgehoben sind (z. B. Windheulen oder der Ton von Pauken).

Wenngleich die Tonhöhe durch eine Frequenz[8] charakterisiert werden kann, ist sie nicht nur eine objektive physikalische Eigenschaft, sondern hat auch eine psychoakustische Komponente. Dies war und ist ein zentrales Problem und Gegenstand andauernder Forschungen in Bezug auf Sprachsynthese und ihre Wahrnehmung über das Gehör[9]. Für die Psychoakustik ist interessant, wie hoch oder tief Töne bestimmter Frequenz wahrgenommen werden. Hierzu wird eine eigene Tonhöhen-Skala aufgebaut, die wahrgenommene Tonhöhe. Die wahrgenommene Tonhöhe wird auch als Tonheit bezeichnet.

Ursprung der Begriffsverwendung

In vielen Sprachen werden Töne im Vergleich miteinander „höher“ oder „tiefer“ genannt, und Melodien (d. h. Abfolgen von Tönen) werden als „ansteigend“ oder „abfallend“ empfunden und bezeichnet.

Diese „räumlichen“ Bezeichnungen beruhen wahrscheinlich auf dem statistischen Vorkommen von in der Natur auftretenden Tönen und Geräuschen, die entsprechend räumlich wahrgenommen und als „von oben“ oder „von unten“ identifiziert werden.[10] Die zahlenmäßig größere (hohe) oder kleinere (niedrige) Frequenz eines Tons passt zwar zu dieser Bezeichnungsweise. Sie kann aber nicht deren Ursache sein, denn die Erkenntnis, dass Töne auf Schwingungen beruhen, ist viel jünger als die Sprachen.

Musikalische Tonhöhe

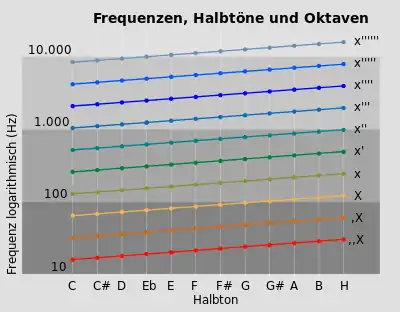
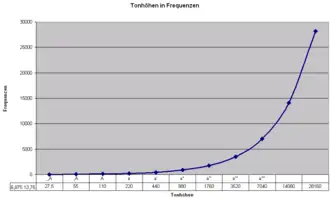
Zusammenhang von Frequenz, Halbton und Oktave

Frequenzen (in Hertz) des Kammertons a¹ und seiner Oktavverwandten

In der Musik ist die Tonhöhe eine Maßangabe (Parameter), die getrennt von anderen Maßangaben oder Eigenschaften beschrieben werden kann. Dabei enthält der Begriff eine lineare und eine helikale (schraubenförmige) Komponente. Die lineare Tonhöhenwahrnehmung, mit der eine annähernd geometrische Veränderung der zugrunde liegenden Schwingungsfrequenzen einhergeht, ist oft an den Eindruck einer linearen Änderung von Helligkeit oder Höhen-Lokalisierung im eigenen Körper (Brust bis Kopf) gekoppelt. Die helikale Komponente drückt sich darin aus, dass die – bei Verdopplung oder Halbierung der Frequenz – eine Oktave höher bzw. tiefer klingenden Töne als ähnlich oder gleich empfunden werden. Töne, die eine oder mehrere Oktaven Abstand haben, fasst man deshalb in einer Tonklasse mit gleicher Tonigkeit zusammen und bezeichnet sie mit demselben Namen (ggf. mit einem Zusatz zur Kennzeichnung des Oktavraums).

Absolute und relative Tonhöhe

Für musikalische Zwecke sollen aufeinander folgende oder zusammen erklingende Töne „gut klingen“. Dies ist aber nur der Fall, wenn diese Töne bestimmte Frequenzverhältnisse einhalten, nämlich die von musikalischen Intervallen. Die für musikalische Zwecke sinnvollen Frequenzverhältnisse fasst man in Tonleitern zusammen. Die Bezeichnung des Tonleiter-Tons wird dann als Bezeichnung der (relativen) musikalischen Tonhöhe verwendet.

Wird zusätzlich noch die Frequenz eines Referenztons angegeben, kann man jedem musikalischen Ton auch eine absolute Tonhöhe zuordnen. Üblicherweise gibt das heutige Notenbild absolute Tonhöhen wieder; maßgeblich ist dabei die Festlegung des Tons a¹ als sogenannter Kammerton auf 440 Hz, die von der internationalen Stimmtonkonferenz von 1939 in London vereinbart wurde. Zur schriftlichen Notation der Tonhöhe sind mehrere Tonsymbol-Systeme in Gebrauch.

Der Charakter einer Melodie oder eines Akkords ist jedoch im Wesentlichen unabhängig von der absoluten Tonlage. Melodien oder Akkorde können z. B. als Ganzes um Intervalle verschoben werden (Transponieren). Die absolute Tonhöhe, mit der ein Musikstück wirklich vorgetragen wird, beruht auf Entscheidung der Musiker, auf den gegebenen stimmlichen Möglichkeiten der Sänger und ggf. den Eigenschaften der verwendeten Instrumente:

Beim unbegleiteten Gesang (A cappella) bestimmen die gegebenen Stimmlagen der Sänger die verwendeten Tonhöhenbereiche. Zur genauen Einstimmung benutzt der Chorleiter beispielsweise eine Stimmgabel.
Instrumente, die nicht leicht umgestimmt werden können, wie Orgel, Klavier oder Akkordeon bestimmen die verwendeten absoluten Tonhöhen. Blas- und Streichinstrumente lassen sich dagegen in ihrer Stimmung in begrenztem Umfang an die genannten Instrumente anpassen.

Absolutes, relatives und Intonationsgehör

Einige wenige Menschen verfügen über ein sogenanntes absolutes Gehör (auch Tonhöhengedächtnis). Sie sind in der Lage, einen Ton ohne Hilfsmittel zu benennen und nach vorgegebener Tonbezeichnung korrekt zu singen.

Vom absoluten Gehör zu unterscheiden ist das relative Gehör, das dazu befähigt, das Intervall zweier aufeinander folgender Töne zu benennen und bei abstrakter Vorgabe (vom Blatt) korrekt zu singen. Sowohl das relative als auch das absolute Gehör kann gezielt trainiert werden.

Ein weiterer Aspekt des musikalischen Gehörs ist die Fähigkeit, Unsauberkeiten in der Intonation – also geringe Abweichungen der Tonhöhe von einem musikalisch geplanten Wert – zu erkennen. Sie wird Intonationsgehör genannt. Diese Fähigkeit hat ihre physiologische Grenze in der Frequenzunterscheidung des Gehörs. Auch diese Grenze ist jedoch durch Training verschiebbar. Versuche haben gezeigt, dass bereits acht Stunden Training genügen,[11] um an die Fähigkeit der Frequenzunterscheidung von geschulten Musikern heranzukommen. Das Intonationsgehör benötigt allerdings in der musikalischen Praxis weit mehr als eine trainierte Frequenzunterscheidung. Hier ist es nämlich erforderlich, vorgestellte Tonhöhen mit realisierten abzugleichen. Bei geübten Sängern ist eine durchschnittliche Abweichung von drei Cent (3/100 Halbton) gemessen worden.[12] Messungen am Düsseldorfer Institute of Stringed Instruments Guitar & Lute ergaben, dass die Tonhöhe als korrekt empfunden wird, wenn die Intonation innerhalb eines Bereichs von etwa 1 Cent erfolgt.[13]

Tonhöhenunschärfe

Sowohl die objektive Messung als auch die subjektive Wahrnehmung von Tonhöhen ist mit einer gewissen Ungenauigkeit („Unschärfe“) behaftet, die teils auf physikalischen, teils auf hörphysiologischen Gegebenheiten beruht.

Physikalisch bedingte Unschärfe

Frequenz und Zeit sind verknüpfte (konjugierte) Größen und gehorchen somit einer „Unschärferelation“[14], wie es auch bei der Fourier-Transformation und deren Anwendungen deutlich wird. Die Unschärferelation bewirkt, dass die Frequenz nicht für einen punktgenauen Moment, sondern nur für eine bestimmte Dauer mehr oder weniger genau gemittelt werden kann.[15] So ließe sich etwa die Frequenz eines periodischen Schallereignisses nur dann absolut exakt messen, wenn seine Zeitdauer völlig unbestimmt, also unendlich wäre. Umgekehrt wird seine Tonhöhe umso unbestimmter, je kürzer die Dauer ist. Hieraus resultiert für die Musizierpraxis die nützliche Erkenntnis, dass bei langsamen Passagen (lange Töne) Intonationsgenauigkeit viel wichtiger (weil hörbarer) ist als bei schnellen Passagen (kurze Töne). So sagen Streicher häufig – zur Überraschung von Laien –, dass es keineswegs leichter ist, langsame Stücke zu spielen.

Hörphysiologisch bedingte Unschärfe

Nach Frequenzanalyse und Umwandlung zu Nervenimpulsen im Innenohr erfolgt eine Weiterleitung in frequenzspezifischen Nervenbahnen, die zusätzlich noch in mehreren parallele Stränge der Hörbahn vervielfacht werden. Die Weiterverarbeitung erfolgt auf mehreren Ebenen im Gehirn. Dieser Vorgang ist wesentlich komplexer als etwa eine einfache technische Spektralanalyse.[16] Wie die Dekodierung von Periodizität beim Hören aus dem Strom der Nervenimpulse im auditorischen Mittelhirn (Colliculi inferiores) arbeitet ist nicht ausreichend geklärt, eine Hypothese beschreibt die Funktion nach dem Prinzip des Koinzidenz-Detektors.[17][18][19] Erwiesen ist, dass mehrere Signalperioden erforderlich sind, damit eine Periodizität – und damit die Basisinformation für die nachfolgende Repräsentation von Tonhöhe im Großhirn – registriert werden kann. Interessanterweise wird die Tonhöhe eines natürlichen Tons von 100 Hz, mit Obertönen, mehr als viermal so schnell wahrgenommen wie ein Sinuston derselben Frequenz.[20], da das Gehirn auch die Ströme der Nervenimpulse nutzt, die von Obertönen ausgelöst werden.

Ein sinusförmiges Schallsignal, das z. B. nur die Dauer einer Halbperiode hat, wird vom Gehör nicht als Ton, sondern als Knackgeräusch mit unbestimmter Tonhöhe wahrgenommen. Die Minimalzeit zur Auslösung einer diskreten Tonhöhenempfindung ist von der Frequenz abhängig. „Für ein Sinussignal von 1000 Hz liegt dieser Zeitwert bei etwa 12 ms; es braucht also ungefähr 12 Perioden, damit ein Sinussignal mit der Frequenz f = 1000 Hz vom Ohr als Tonhöhe erfasst werden kann. 3 bis 4 Perioden sind notwendig für ein Signal von 200 Hz, ungefähr 250 für ein solches von 10 kHz.“[21]

Wahrgenommene Tonhöhe (Tonheit)

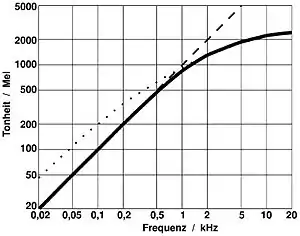
Zusammenhang zwischen Frequenz und wahrgenommener Tonhöhe (siehe auch Bildtext)

Die Tonheit ist in der Psychoakustik eine Empfindungsgröße mit der Maßeinheit Mel, anhand derer man Schallereignisse bezüglich ihrer empfundenen Tonlage ordnen kann. Im Bild rechts ist dargestellt, wie sich anhand von Hörversuchen der Zusammenhang zwischen der Frequenz eines Sinustons und der wahrgenommenen Tonhöhe ergibt. Für komplexe „Töne“ (streng genommen: Klänge im Sinne von Teiltonkomplexen), wie sie in der Realität vorkommen (Schwingende Systeme), gelten diese Empfindungsgrößen der Psychoakustik nicht direkt, und die Abweichungen von der Frequenzskala liegt bis 5 kHz innerhalb der vom Ohr noch nicht wahrnehmbaren Grenzen.[22]

Die Wahrnehmung der Tonhöhe ist eng verbunden mit der Physiologie des Innenohres und des auditorischen Gehirns. Das Innenohr führt eine Frequenzanalyse des gehörten Signals durch. Unterschiedliche Frequenzen führen an unterschiedlichen Orten des Innenohrs zu einer Erregung von Nervenzellen. Der Ort, an dem Nervenzellen verstärkt angeregt werden, kann so zur Bestimmung der Tonhöhe benutzt werden. Die genauen Details der Funktion sind nach wie vor Gegenstand der Forschung und es gibt mehrere Modelle dafür.[16]

Bei der Wahrnehmung der Tonhöhe spielt die Zusammensetzung des Tons aus Grundton und Obertönen eine wichtige Rolle. Da für die Tonhöhenwahrnehmung die Periode des Tons wichtig ist, bestimmen z. B. bei nicht hörbarem Grundton die wahrnehmbaren bzw. hörbaren Anteile der Obertöne die empfundene Tonhöhe. Dies steht im Zusammenhang mit dem Residualton, den das menschliche Ohr aus einem Frequenzgemisch bildet. So bleibt die Periode eines Tons nur dann erhalten, wenn der größte gemeinsame Teiler der Obertonfrequenzen wieder den Grundton abbildet. Dies passiert zwar selten in einer natürlichen Umgebung, ist aber grundsätzlich möglich. Besteht z. B. ein Ton aus Grundton und seinen ersten zwei Obertönen und werden dann Grundton und erster Oberton unhörbar, erscheint der Ton eine Oktave und eine Quinte höher. Das kann mit dem größten gemeinsamen Teiler (ggT) berechnet werden. Ist der Grundton z. B. 100 Hz, liegen die ersten zwei Obertöne auf 200 Hz und 300 Hz. Der ggT von 100, 200, 300 ist dann 100. Fehlt der Grundton, errechnet sich die Grundtonhöhe aus 200 und 300, was immer noch 100 ist. Fehlt aber auch der erste Oberton, ist klar, dass der ggT von 100 und 300 eben 100 ist. Dieser Effekt kann dann auftreten, wenn z. B. ein Instrument gefiltert wird oder von anderen Klängen so überlagert wird, dass bestimmte Frequenzen maskiert bzw. anderen Klängen zugeordnet werden. Auch spielen bei der Empfindung der Tonhöhe das Wissen, das Gedächtnis und die Erwartungen des Hörers eine Rolle. So würde man z. B. Oktaven immer als einen Ton interpretieren, da der ggT oder die Periode in solch einem Frequenzgemisch immer den untersten Grundton ergeben würde. Dies kann das Gehirn anhand des Timbres – also die Gewichtung, Zusammensetzung und Veränderung der Obertöne – einschätzen. Je trainierter bzw. konditionierter der Hörer auf einen bestimmten Klang ist, desto eher nimmt er dabei mehrere Tonhöhen wahr. Das steht auch im Zusammenhang im Erkennen und Wahrnehmen von Akkorden, da das Timbre von dem ggT bei Akkorden selten bei monotonen Klangereignissen vorkommt, da sehr viele der ersten Obertöne fehlen würden und die Periode sehr lang wäre. Deswegen interpretiert das Gehirn in diesen Fällen mehrere Klänge anstatt einen sehr tiefen Ton. Es ist zu beachten, dass das Gehirn nicht mathematisch exakt ermittelt; es hat auch seine Toleranzen. Der ggT ist nur ein mathematisches Hilfsmittel, um anzunähern, wie lang die Periode mehrerer Frequenzen sein wird.

Siehe auch

Mel (Maßeinheit für die wahrgenommene Tonhöhe)
Universalien der Musikwahrnehmung

Literatur

Ernst Terhardt: Zur Tonhöhenwahrnehmung von Klängen:

Psychoakustische Grundlagen. In: Acustica. International Journal on Acoustics, Bd. 26 (1972), S. 173–186, ISSN 0001-7884.
Ein Funktionsschema. In: Acustica. International Journal on Acoustics, Bd. 26 (1972), S. 187–199, ISSN 0001-7884

Ernst Terhardt, Gerhard Stoll, Manfred Seewann: Algorithm for extraction of pitch and pitch salience from complex tonal signals. In: Journal of the Acoustical Society of America, Bd. 71 (1982), Heft 3, S. 679–688, ISSN 0001-4966
Ernst Terhardt: Calculating Virtual Pitch. In: Hearing Research. An international Journal, Jg. 1 (1979), S. 155–182, ISSN 0378-5955
Ernst Terhardt: Akustische Kommunikation. Grundlagen mit Hörbeispielen. Springer Verlag, Berlin 1998, ISBN 3-540-63408-8 (+ 1 CD-ROM).
Eberhard Zwicker, Hugo Fastl: Psychoacoustics. Facts and Models (Springer series in informations sciences; 22). 2. Aufl. Springer Verlag, Berlin 1999, ISBN 3-540-65063-6.
William M. Hartmann: Signals, Sound, and Sensation. Springer, New York 1998, ISBN 1-56396-283-7.[9]
Christopher J. Plack, Andrew J. Oxenham, Richard R. Fay, Arthur N. Popper: Pitch. Neural Coding and Perception (Springer Handbook of Auditory Research; 24). Springer, New York 2005, ISBN 0-387-23472-1.
Lynne A. Werner, Richard R. Fay, Arthur N. Popper: Human Auditory Development. 2012, ISBN 1-4614-1421-0 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
Carryl L. Baldwin: Auditory Cognition and Human Performance: Research and Applications. 2012, ISBN 0-415-32594-3 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
J. A. Simmons, A. Megela Simmons: Bats and frogs and animals in between: evidence for a common central timing mechanism to extract periodicity pitch. In: Journal of comparative physiology. A, Neuroethology, sensory, neural, and behavioral physiology. Band 197, Nummer 5, Mai 2011, ISSN 1432-1351, S. 585–594, doi:10.1007/s00359-010-0607-4, PMID 21072522, PMC 3257830 (freier Volltext) (Review).
Ville Pulkki, Matti Karjalainen: Communication Acoustics: An Introduction to Speech, Audio and Psychoacoustics. John Wiley & Sons, 2015, ISBN 978-1-118-86654-2.

Weblinks

Commons: Pitch (music) – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Tonhöhe – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Roy D. Patterson, Etienne Gaudrain, Thomas C. Walters: Music Perception – The Perception of Family and Register in Musical Tones. 2010, ISBN 978-1-4419-6113-6, S. 38 (englisch, Online in der Google-Buchsuche).
http://www.ansi.org/
„Die Tonhöhe ist definiert als die Eigenschaft einer Hörempfindung nach der Schalle auf einer musikalischen Tonleiter geordnet werden können (ANSI S1.1), mithin auf einem Kontinuum von ‚tief‘ bis ‚hoch‘. Bei Sinustönen ist sie eng mit der Frequenz des Tones verbunden.“ Stefan Weinzierl: Handbuch der Audiotechnik. 2008, ISBN 3-540-34300-8, S. 65 (eingeschränkte Vorschau in der Google-Buchsuche).
“For the purposes of this book we decided to take a conservative approach, and to focus on the relationship between pitch and musical melodies. Following the earlier ASA definition, we define pitch as ‘that attribute of sensation whose variation is associated with musical melodies.’ Although some might find this too restrictive, an advantage of this definition is that it provides a clear procedure for testing whether or not a stimulus evokes a pitch, and a clear limitation on the range of stimuli that we need to consider in our discussions.” Christopher J., Andrew J. Oxenham, Richard R. Fay: Pitch: Neural Coding and Perception. 2005, ISBN 0-387-23472-1, S. 2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
“Melody: In the most general case, a coherent succession of pitches. Here pitch means a stretch of sound whose frequency is clear and stable enough to be heard as not noise; succession means that several pitches occur; and coherent means that the succession of pitches is accepted as belonging together.” Randel, Don Michael: The Harvard Dictionary of Music. 2003, ISBN 978-0-674-01163-2, S. 499 (englisch, Online in der Google-Buchsuche).
„Die Tonhöhe wird durch die Frequenz des Schalls bestimmt, nicht primär durch seine Wellenlänge. […] In Luft und Wasser nimmt man dein gleichen Ton wahr, obwohl die Wellenlängen bei gleicher Frequenz sehr unterschiedlich sind.“ Hartmut Zabel: Kurzlehrbuch Physik. 2010, ISBN 3-13-162521-X, S. 150 (eingeschränkte Vorschau in der Google-Buchsuche).
“Pitch is an important quality of sound, the focus of intense inquiry and investigation since antiquity. Pitch is basic to two forms of behavior specific to humans: speech and music. Pitch is usually understood as a one-dementional precept determined by the period of the stimulus (or its inverse, F0), and insensitive to changes along other stimulus dimensions. However, its complex role within music involves harmonic and melodic effects that go beyond this simple one-dementional model. There is still debate as to where, and how, pitch is extracted within the auditory system.” Christopher J. Plack, David R. Moore: Hearing Olp Series Oxford Handbooks Oxford library of psychology Volume 3 of The Oxford Handbook of Auditory Science, Christopher J. Plack. 2010, ISBN 0-19-923355-1, S. 95 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
Für Menschen hörbare Frequenzen umfassen einen Bereich von 16 bis 20.0000 Hz, und musikalisch brauchbare finden sich zwischen 30 und 5000 Hz. Clemens Kühn: Musiklehre. Laaber-Verlag, Laaber 1980, S. 43.
Hartmann, William Morris: Signals, Sound, and Sensation. 1997, ISBN 1-56396-283-7, S. 145, 284, 287 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
Cesare V. Parisea, Katharina Knorre, Marc O. Ernsta: Natural auditory scene statistics shapes human spatial hearing. PNAS, Band 111, Nr. 16 (2014), S. 6104–6108.
“Pure [Sinus] tones produce a clear, unambiguous pitch, and we are very sensitive to changes in their frequency. For instance, well-trained listeners can distinguish between two tones with frequencies of 1000 and 1002 Hz – a difference of only 0,2 % (Moore, 1973). A semitone, the smallest step in the Western scale system, is a difference of about 6 %, or about a factor of 30 greater then the JND of frequency for pure [Sinus] tones. Perhaps not surprisingly, musicians are generally better then nonmusicans at discriminating small changes in frequency; what is more surpising is that it does not take much practice for people with no musical training to ‘catch up’ with musicians in terms of their performance. In a recent study, […] it took only between 4 and 8 hours of practice […] of the untrained listeners to match those of the trained musicians, […]” Diana Deutsch: The Psychology of Music. 2012, ISBN 0-12-381461-8, S. 9, 10 (eingeschränkte Vorschau in der Google-Buchsuche).
“The average JND for the octave was 16 cents, and JNDs for other intervals of the chromatic scale ranged from 13 to 26 cents. […] for Example, Hagerman and Sundberg (1980) reported that the average intonation accuracy in a sample of expert barbershop songs was less then 3 cents.” Diana Deutsch: The Psychology of Music. 2012, ISBN 0-12-381461-8, S. 124, 125 (eingeschränkte Vorschau in der Google-Buchsuche).
Karl Sandvoss: Konstruktive Grundregeln zum Bau intonationssicherer akustischer Gitarren und das Saitenproblem. Neue Forschungen und Entwicklungen, Teil 2. (Bericht aus dem Institute of Stringed Instruments Guitar & Lute ISIGL Düsseldorf) In: Gitarre & Laute 7, 1985, Heft 1, S. 52–57; hier: S. 52.
„Dass eine Messung eine unvermeidliche Unschärfe hat, ist keine Spezialität der Quantenmechanik, sondern gilt grundsätzlich für alle wellenartigen Phänomene – von Musik bis zum Alphazerfall von Atomkernen.“ Norbert Treitz: Von den falschen Tönen zur Unbestimmtheitsrelation, Das Unschärfe-Prinzip. 2013 (online [PDF]).
„Ihre Ursache ist die Welleneigenschaft des Schalles und die daraus resultierende Unbestimmtheit der Frequenz bei kurzen Signalen. Der Begriff ‚Frequenz‘, wie er üblicherweise gebraucht wird, impliziert ein sich für alle Zeiten exakt periodisch wiederholendes Signal. In einem zeitveränderlichen Signal hängt die Gültigkeit des Begriffes von der Beobachtungsdauer bzw. von der Veränderungsrate ab; es gibt nur so etwas wie unscharfe ‚momentane Frequenzen‘. Ein extrem kurzes Signal ‚hat‘ keine Frequenz mehr (verkürzt man eine harmonische Schwingung schrittweise, so wird nach und nach aus dem Ton ein Geräusch).“ Thomas Görne: Tontechnik. 2. Auflage. Carl Hanser Verlag, München 2008, ISBN 978-3-446-41591-1, S. 148 ff. (online in der Google-Buchsuche)
“Effects of Peripheral Tuning on the Auditory Nerve’s Representation of Speech Envelope and Temporal Fine Structure Cues.” Enrique A. Lopez-Poveda, A. Alan R. Palmer, Ray Meddis: The Neurophysiological Bases of Auditory Perception. 2010, ISBN 1-4419-5686-7 (englisch, Online in der Google-Buchsuche).
“The mechanism by which neurons process the coding of signals is not well understood. Here, we propose that coincidence detection, […]” Yueling Chen, Hui Zhang, Hengtong Wang, Lianchun Yu,Yong Chen: The Role of Coincidence-Detector Neurons in the Reliability and Precision of Subthreshold Signal Detection in Noise. 2013 (englisch, online [PDF]).
“the principles that govern the relationship between natural sound ensembles and observed responses in neurophysiological studies remain unclear.” Michael A. Carlin, Mounya Elhilal: Sustained Firing of Model Central Auditory Neurons Yields a Discriminative Spectro-temporal Representation for Natural Sounds. 2013 (englisch, online).
J. A. Simmons, A. Megela Simmons: Bats and frogs and animals in between: evidence for a common central timing mechanism to extract periodicity pitch. In: Journal of comparative physiology. A, Neuroethology, sensory, neural, and behavioral physiology. Band 197, Nummer 5, Mai 2011, ISSN 1432-1351, S. 585–594, doi:10.1007/s00359-010-0607-4, PMID 21072522, PMC 3257830 (freier Volltext) (Review).
“The 100 Hz pitch associated with the fundamental is acquired in under 20 ms, whereas that of 100 Hz sinusoid takes in excess 80 ms.” Roy D. Patterson, Robert W. Peters, Robert Milroy: Threshold duration for melodic pitch. In: Rainer Klinke, Rainer Hartmann: Hearing, physiological bases and psychophysics. Proceedings of the 6th International Symposium on Hearing, Bad Nauheim, Germany, April 5–9, 1983. Springer, Berlin/Heidelberg/New York/Tokyo 1983, ISBN 3-540-12618-X, S. 321–326 (PDF).
Werner Kaegi: Was ist elektronische Musik. Orell Füssli, Zürich 1967, S. 63.
“There is some psychoacostical evidence for both place and temporal codes. One piece of evidence in favor of a temporal code is that pitch discrimination abilities deteriorate at frequencies above 4 to 5 kHz – the same frequency range above which listeners’ ability to recognize familiar melodies (Oxenham, Micheyl, Keebler, Loper, & Santurette, 2011), degrades. […]” Diana Deutsch: The Psychology of Music. 2012, ISBN 0-12-381461-8, S. 11 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Patterson-1] Roy D. Patterson, Etienne Gaudrain, Thomas C. Walters: Music Perception – The Perception of Family and Register in Musical Tones. 2010, ISBN 978-1-4419-6113-6, S. 38 (englisch, Online in der Google-Buchsuche).

[2] ttp://www.ansi.org/

[Stefan_Weinzierl-3] „Die Tonhöhe ist definiert als die Eigenschaft einer Hörempfindung nach der Schalle auf einer musikalischen Tonleiter geordnet werden können (ANSI S1.1), mithin auf einem Kontinuum von ‚tief‘ bis ‚hoch‘. Bei Sinustönen ist sie eng mit der Frequenz des Tones verbunden.“ Stefan Weinzierl: Handbuch der Audiotechnik. 2008, ISBN 3-540-34300-8, S. 65 (eingeschränkte Vorschau in der Google-Buchsuche).

[Christopher_J-4] “For the purposes of this book we decided to take a conservative approach, and to focus on the relationship between pitch and musical melodies. Following the earlier ASA definition, we define pitch as ‘that attribute of sensation whose variation is associated with musical melodies.’ Although some might find this too restrictive, an advantage of this definition is that it provides a clear procedure for testing whether or not a stimulus evokes a pitch, and a clear limitation on the range of stimuli that we need to consider in our discussions.” Christopher J., Andrew J. Oxenham, Richard R. Fay: Pitch: Neural Coding and Perception. 2005, ISBN 0-387-23472-1, S. 2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).

[Randel-5] “Melody: In the most general case, a coherent succession of pitches. Here pitch means a stretch of sound whose frequency is clear and stable enough to be heard as not noise; succession means that several pitches occur; and coherent means that the succession of pitches is accepted as belonging together.” Randel, Don Michael: The Harvard Dictionary of Music. 2003, ISBN 978-0-674-01163-2, S. 499 (englisch, Online in der Google-Buchsuche).

[Kurzlehrbuch_Physik-6] „Die Tonhöhe wird durch die Frequenz des Schalls bestimmt, nicht primär durch seine Wellenlänge. […] In Luft und Wasser nimmt man dein gleichen Ton wahr, obwohl die Wellenlängen bei gleicher Frequenz sehr unterschiedlich sind.“ Hartmut Zabel: Kurzlehrbuch Physik. 2010, ISBN 3-13-162521-X, S. 150 (eingeschränkte Vorschau in der Google-Buchsuche).

[David_Moore-7] “Pitch is an important quality of sound, the focus of intense inquiry and investigation since antiquity. Pitch is basic to two forms of behavior specific to humans: speech and music. Pitch is usually understood as a one-dementional precept determined by the period of the stimulus (or its inverse, F0), and insensitive to changes along other stimulus dimensions. However, its complex role within music involves harmonic and melodic effects that go beyond this simple one-dementional model. There is still debate as to where, and how, pitch is extracted within the auditory system.” Christopher J. Plack, David R. Moore: Hearing Olp Series Oxford Handbooks Oxford library of psychology Volume 3 of The Oxford Handbook of Auditory Science, Christopher J. Plack. 2010, ISBN 0-19-923355-1, S. 95 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).

[8] Für Menschen hörbare Frequenzen umfassen einen Bereich von 16 bis 20.0000 Hz, und musikalisch brauchbare finden sich zwischen 30 und 5000 Hz. Clemens Kühn: Musiklehre. Laaber-Verlag, Laaber 1980, S. 43.

[hartmann-9] Hartmann, William Morris: Signals, Sound, and Sensation. 1997, ISBN 1-56396-283-7, S. 145, 284, 287 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).

[10] Cesare V. Parisea, Katharina Knorre, Marc O. Ernsta: Natural auditory scene statistics shapes human spatial hearing. PNAS, Band 111, Nr. 16 (2014), S. 6104–6108.

[Pitch_of_sinus_tones-11] “Pure [Sinus] tones produce a clear, unambiguous pitch, and we are very sensitive to changes in their frequency. For instance, well-trained listeners can distinguish between two tones with frequencies of 1000 and 1002 Hz – a difference of only 0,2 % (Moore, 1973). A semitone, the smallest step in the Western scale system, is a difference of about 6 %, or about a factor of 30 greater then the JND of frequency for pure [Sinus] tones. Perhaps not surprisingly, musicians are generally better then nonmusicans at discriminating small changes in frequency; what is more surpising is that it does not take much practice for people with no musical training to ‘catch up’ with musicians in terms of their performance. In a recent study, […] it took only between 4 and 8 hours of practice […] of the untrained listeners to match those of the trained musicians, […]” Diana Deutsch: The Psychology of Music. 2012, ISBN 0-12-381461-8, S. 9, 10 (eingeschränkte Vorschau in der Google-Buchsuche).

[JND_complex_tones-12] “The average JND for the octave was 16 cents, and JNDs for other intervals of the chromatic scale ranged from 13 to 26 cents. […] for Example, Hagerman and Sundberg (1980) reported that the average intonation accuracy in a sample of expert barbershop songs was less then 3 cents.” Diana Deutsch: The Psychology of Music. 2012, ISBN 0-12-381461-8, S. 124, 125 (eingeschränkte Vorschau in der Google-Buchsuche).

[13] Karl Sandvoss: Konstruktive Grundregeln zum Bau intonationssicherer akustischer Gitarren und das Saitenproblem. Neue Forschungen und Entwicklungen, Teil 2. (Bericht aus dem Institute of Stringed Instruments Guitar & Lute ISIGL Düsseldorf) In: Gitarre & Laute 7, 1985, Heft 1, S. 52–57; hier: S. 52.

[spektrum-14] „Dass eine Messung eine unvermeidliche Unschärfe hat, ist keine Spezialität der Quantenmechanik, sondern gilt grundsätzlich für alle wellenartigen Phänomene – von Musik bis zum Alphazerfall von Atomkernen.“ Norbert Treitz: Von den falschen Tönen zur Unbestimmtheitsrelation, Das Unschärfe-Prinzip. 2013 (online [PDF]).

[Thomas_Görne-15] „Ihre Ursache ist die Welleneigenschaft des Schalles und die daraus resultierende Unbestimmtheit der Frequenz bei kurzen Signalen. Der Begriff ‚Frequenz‘, wie er üblicherweise gebraucht wird, impliziert ein sich für alle Zeiten exakt periodisch wiederholendes Signal. In einem zeitveränderlichen Signal hängt die Gültigkeit des Begriffes von der Beobachtungsdauer bzw. von der Veränderungsrate ab; es gibt nur so etwas wie unscharfe ‚momentane Frequenzen‘. Ein extrem kurzes Signal ‚hat‘ keine Frequenz mehr (verkürzt man eine harmonische Schwingung schrittweise, so wird nach und nach aus dem Ton ein Geräusch).“ Thomas Görne: Tontechnik. 2. Auflage. Carl Hanser Verlag, München 2008, ISBN 978-3-446-41591-1, S. 148 ff. (online in der Google-Buchsuche)

[Enrique_A-16] “Effects of Peripheral Tuning on the Auditory Nerve’s Representation of Speech Envelope and Temporal Fine Structure Cues.” Enrique A. Lopez-Poveda, A. Alan R. Palmer, Ray Meddis: The Neurophysiological Bases of Auditory Perception. 2010, ISBN 1-4419-5686-7 (englisch, Online in der Google-Buchsuche).

[journalpone-17] “The mechanism by which neurons process the coding of signals is not well understood. Here, we propose that coincidence detection, […]” Yueling Chen, Hui Zhang, Hengtong Wang, Lianchun Yu,Yong Chen: The Role of Coincidence-Detector Neurons in the Reliability and Precision of Subthreshold Signal Detection in Noise. 2013 (englisch, online [PDF]).

[journalpone2-18] “the principles that govern the relationship between natural sound ensembles and observed responses in neurophysiological studies remain unclear.” Michael A. Carlin, Mounya Elhilal: Sustained Firing of Model Central Auditory Neurons Yields a Discriminative Spectro-temporal Representation for Natural Sounds. 2013 (englisch, online).

[PMID21072522-19] J. A. Simmons, A. Megela Simmons: Bats and frogs and animals in between: evidence for a common central timing mechanism to extract periodicity pitch. In: Journal of comparative physiology. A, Neuroethology, sensory, neural, and behavioral physiology. Band 197, Nummer 5, Mai 2011, ISSN 1432-1351, S. 585–594, doi:10.1007/s00359-010-0607-4, PMID 21072522, PMC 3257830 (freier Volltext) (Review).

[PattersonPDF-20] “The 100 Hz pitch associated with the fundamental is acquired in under 20 ms, whereas that of 100 Hz sinusoid takes in excess 80 ms.” Roy D. Patterson, Robert W. Peters, Robert Milroy: Threshold duration for melodic pitch. In: Rainer Klinke, Rainer Hartmann: Hearing, physiological bases and psychophysics. Proceedings of the 6th International Symposium on Hearing, Bad Nauheim, Germany, April 5–9, 1983. Springer, Berlin/Heidelberg/New York/Tokyo 1983, ISBN 3-540-12618-X, S. 321–326 (PDF).

[Werner_Kaegi-21] Werner Kaegi: Was ist elektronische Musik. Orell Füssli, Zürich 1967, S. 63.

[Diana_Deutsch-22] “There is some psychoacostical evidence for both place and temporal codes. One piece of evidence in favor of a temporal code is that pitch discrimination abilities deteriorate at frequencies above 4 to 5 kHz – the same frequency range above which listeners’ ability to recognize familiar melodies (Oxenham, Micheyl, Keebler, Loper, & Santurette, 2011), degrades. […]” Diana Deutsch: The Psychology of Music. 2012, ISBN 0-12-381461-8, S. 11 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).