Geoidbestimmung
Geoidbestimmung bezeichnet in der Geodäsie Verfahren zur Definition des Geoids.

Das Geoid ist diejenige Niveaufläche des Schwerefelds der Erde, die mit dem mittleren Meeresspiegel der Weltmeere zusammenfällt und sich auf Meereshöhe unter den Kontinenten fortsetzt. Es stellt als idealisierte Form der Erdoberfläche für die Geowissenschaften die Erdfigur theoretisch dar und dient als Bezugsfläche für fast alle gebräuchlichen Höhensysteme. Daher ist die genaue Bestimmung des Geoids auch praktisch von grundlegender Bedeutung für die Landesvermessung und für die Transformation verschiedener Höhensysteme.
Diese Aufgabe ist eng mit der Bestimmung von Details des Erdschwerefeldes verbunden. Die Methoden zur Messung der benötigten physikalischen Parameter des Erdschwerefelds wie auch die mathematischen Modelle zur Auswertung der erfassten Daten werden laufend weiterentwickelt und sind Gegenstand zahlreicher Forschungsprojekte. Die erreichbaren Genauigkeiten haben sich in den letzten fünf Jahrzehnten nahezu verzehnfacht. Das um 1990 postulierte Zentimeter-Geoid wurde noch nicht erreicht, in den Industriestaaten liegt die Genauigkeit bei 3–5 cm (Stand 2017).
Globale und regionale Geoidbestimmung
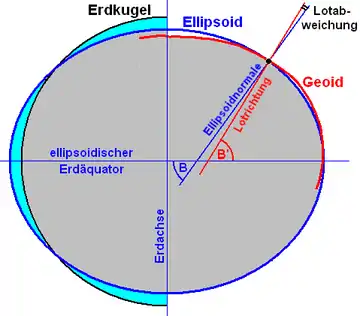
Jede konkrete Geoidbestimmung bezieht sich üblicherweise auf eine mathematisch klar definierte Referenzfläche, wofür entweder das mittlere Erdellipsoid oder das Referenzellipsoid der jeweiligen Landesvermessung dient. Die Distanz zu dem gewählten Ellipsoid, gemessen längs der Ellipsoidnormalen, bezeichnet man als Geoidhöhe. Die Referenzellipsoide – von denen weltweit etwa 200 in Gebrauch sind – wurden in den Industriestaaten vor etwa 100 Jahren festgelegt und schmiegen sich dem Geoid des jeweiligen Staatsgebietes möglichst gut an. Von einem global gemittelten Erdellipsoid können sie – je nach Lage ihrer Fundamentalpunkte – um Beträge zwischen 10 und 100 Meter in der Höhe abweichen.
Das globale Erdellipsoid kann heute auf wenige Zentimeter genau berechnet werden, wozu die Satellitengeodäsie wesentlich beiträgt. Um 1960 waren dessen Halbachsen auf etwa 30 Meter bekannt, was bei einem mittleren Erdradius von 6.370 km immerhin einer relativen Genauigkeit von fünf Millionstel entspricht (0,0005 Prozent oder 5 mm/km). Lokale Vermessungen kommen auch heute meist mit dieser Präzision aus (etwa 1 mm bei technischen Bauwerken), doch bei regionalen und globalen Projekten steigen die Anforderungen inzwischen deutlich. Sie können mit dem Global Positioning System (GPS) oder der Very Long Baseline Interferometry (VLBI) bereits im Bereich von 10−8 bis 10−9 liegen, wenige Milliardstel, was in den letzten Jahrzehnten nach hochpräzisen Methoden der Geoidbestimmung verlangt.
Die Form des Geoids als einer besonderen Niveaufläche des Schwerepotentials wird einerseits von der globalen Erdfigur und dem Aufbau des Erdinneren geprägt, andrerseits von allen Unregelmäßigkeiten der Erdkruste. Dementsprechend unterscheidet man zwischen „langwelligen“ Strukturen – die am besten durch Auswertung von Satellitenbahnen zu bestimmen sind – und den „kurzwelligen“ Anteilen, die von der Landschaft und Geologie der jeweiligen Region geprägt werden. Letztere sind – insbesondere im Gebirge – nur durch lokale, terrestrische Messungen bestimmbar.
Die langwelligen Geoidundulationen der verschiedenen Kontinente betragen etwa 20 bis 50 Meter, die regional-lokalen Effekte einige Meter. Sie können sich jedoch – z. B. im steilen Gelände eines Gebirgslandes – um einige Dezimeter pro Kilometer ändern. Zur Berechnung solcher variabler Einflüsse benötigt man neben einem guten Vermessungsnetz auch ein genaues Geländemodell und ein digitales Modell der örtlichen Gesteinsdichte.
Geoidbestimmung als interdisziplinäre Aufgabe
Zu den modernen Methoden der Geoidbestimmung müssen daher die verschiedensten Wissensgebiete beitragen: Mathematische Geodäsie und Netzausgleichung, Gravimetrie und astronomisch-geodätische Messtechnik, Radartechnik und Telemetrie, die Analyse von Satellitenbahnen (siehe auch Satellitentechnik und Bahnstörungen), genaue Grundlagen für die erforderlichen Bezugsysteme, sowie Daten aus der Geologie und Ozeanografie.
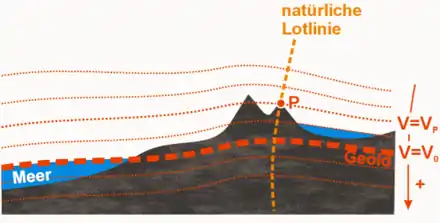
Während das Geoid auf den Ozeanen durch den als ruhend gedachten mittleren Meeresspiegel repräsentiert wird, muss man es sich unter den Kontinenten als dessen Fortsetzung – etwa als Wasserstand in einem gedachten System von Kanälen – vorstellen. Es ist hier der Messung nur indirekt zugänglich, sodass die genaue Geoidbestimmung schon seit langem zu den anspruchsvollsten Aufgaben der Höheren Geodäsie zählt. In den 1990er Jahren wurde für diese Herausforderung der Begriff des Zentimeter-Geoids geprägt.
Demgegenüber ist das ozeanische Geoid zwar weniger genau messbar, aber einer direkten Bestimmung zugänglich, z. B. durch Radar-Höhenmessung von Satelliten über dem Meeresspiegel. Allein die Entwicklung dieser Satellitenaltimetrie und ihrer mathematischen Auswertung unter dem Einfluss von Gezeiten hat in den 1970er und 1980er Jahren weltweit an die tausend Wissenschaftler verschiedenster Gebiete beschäftigt.
Physikalisch-geometrische und historische Aspekte
Die Ermittlung des Geoids als der Fläche gleichen Schwerepotentials in mittlerer Meereshöhe und seiner Abweichungen vom international vereinbarten Bezugsellipsoid sowie dessen Verbesserung ist das Programm der klassischen Geodäsie.
Obwohl das Geoid eine physikalisch definierte Bezugsfläche ist, die aus der (variablen) Gravitationskraft und der Erdrotation resultiert, lässt es sich am genauesten geometrisch bestimmen: nämlich durch Messung der Lotrichtung, auf welcher es überall senkrecht steht. Die klassische Geoidbestimmung, deren Theorie Friedrich Robert Helmert bereits vor 120 Jahren entwickelt hat, sucht jene Fläche, die von allen gemessenen Lotrichtungen senkrecht durchstoßen wird (siehe Potsdamer Schweresystem). Da die Messung der sogenannten Lotabweichungen im Koordinatensystem der Sterne erfolgt, wird diese älteste Methode der Geoidbestimmung auch „astro-geodätisch“ genannt und ein damit berechnetes regionales Geoid als „Astrogeoid“ bezeichnet.
In den 1940er-Jahren wurde die Geoidbestimmung durch physikalische Methoden ergänzt, insbesondere durch die Entwicklung genauer Gravimeter zur relativen Schweremessung und die Eötvös’sche Drehwaage, die auch zur unterirdischen Exploration von Erdölfeldern diente. Gleichzeitig entwickelten nordeuropäische Geodäten die Theorie der Isostasie (Schwimmgleichgewicht der Gebirge und Kontinente), wodurch erstmals weltweite Berechnungen möglich wurden.
Durch Kombination der Bestimmungsverfahren von gravimetrischem Geoid und Astro-Geoid konnte man zur Mitte des 20. Jahrhunderts das globale Geoid auf 5–10 Meter genau berechnen, auf dem Festland regional – je nach messtechnischem Aufwand – auf 20 bis 100 Zentimeter.
Weil sich die Unregelmäßigkeiten von Schwerefeld und Geoid auch in der Bewegung von Erdsatelliten widerspiegeln, entstanden seit den 1960er Jahren eine Reihe von Methoden der Satellitengeodäsie sowie zugehörige mathematische Verfahren zur sogenannten Feldfortsetzung nach unten (vom Niveau der Satellitenbahn herab auf das Meeresniveau). Sie erforderten auch die Etablierung neuer interdisziplinärer Forschungsfelder – beispielsweise die Kollokation (gemeinsame Behandlung geometrisch-physikalischer Effekte) oder die Physikalische Geodäsie.
Zusammenfassung: Da das Geoid eine Folge sowohl der physikalischen Massenverteilung im Erdinnern wie auch der Topografie des Geländes ist und zugleich die (geometrische) Bezugsfläche unserer Höhensysteme darstellt, können sehr verschiedene Verfahren zur Geoidbestimmung herangezogen werden. Sie entfallen methodisch auf die folgenden vier Gruppen:
Methodengruppen zur Geoidbestimmung
Messungen der Schwerkraft
(siehe auch Gravimetrie)
- terrestrische Messungen mit Gravimetern
- Schweremessungen im Flugzeug
- Messung von Schweregradienten
- Drehwaagen-Messungen (Messprinzip nach Eötvös u. a.)
- Höhendifferenz-Messungen mit hochpräzisen Gravimetern
Messungen von Lotabweichungen
(siehe auch Astrogeoid und astronomisches Nivellement)
- Messung von astro-geodätischen Lotabweichungen
- mit Astrolabien (Danjon, Ni2, Zirkumzenital)
- mit Theodoliten oder Durchgangs-Instrumenten
- mit einer Zenitkamera oder (an festen Stationen) mit einem PZT
- terrestrisch – Tachymetrie oder trigonometrische Höhenmessung
- aus astronomischen Azimuten in Vermessungsnetzen (nur bis etwa 1970 von Bedeutung)

Messungen mittels Erdsatelliten
- durch Analyse von Bahnstörungen – siehe auch Bahnbestimmung
- mittels Schwerepotential und Kugelfunktionen
- mittels Potential der einfachen Schicht (Methode H. R. Koch, ca. 1970–1990)
- durch Gradiometrie und SST
- Satellitengradiometrie – siehe Forschungssatellit GOCE
- Satellite-to-Satellite Tracking (Distanzänderungen zweier Satelliten), siehe z. B. GRACE
- mit Satelliten-Altimetrie (Radarechos über dem Meer, künftig auch über größeren Eisflächen)
Kombination einiger obgenannter Verfahren bzw. Daten
- astro-gravimetrische Geoidbestimmung (TU München & Wien, z. B. Prof. Hein, W. Daxinger)
- Kollokation von geometrischen und physikalischen Schwerefelddaten
- Störpotential mittels Kugelfunktions-Entwicklung plus terrestrische Gravimetrie
Literatur
- Karl Ledersteger: Astronomische und Physikalische Geodäsie (Erdmessung). JEK Band V, Kapitel 4 (Lotabweichung und Geoidbestimmung), 7 (Kugelfunktionen) und 12/13 (Geoidundulationen, Molodenskij, Weltsystem), J. B. Metzler-Verlag, Stuttgart 1968.
- Fernando Sansò, Michael Sideris (Hrsg.): Geoid Determination: Theory and Methods. (Vorausinfo) Springer-Verlag, November 2007, ISBN 0-387-46386-0, 300 Seiten.
- Jean-Jacques Levallois: Géodésie générale, IAG, Paris 1969.
- Gottfried Gerstbach: Regionale Geoidbestimmung. Geowiss. Mitt. Band 11, TU Wien 1975.
- Siegfried Heitz: Geoidbestimmung durch Interpolation nach kleinsten Quadraten aufgrund gemessener und interpolierter Lotabweichungen. DGK Reihe C, Heft 124, München/Frankfurt 1968, 39 Seiten.
- Albrecht Preusser: Ein dreidimensionales Berechnungsmodell für geodätische Punkt- und Geoidbestimmungen. DGK Reihe C, Heft 238, München 1977, 102 Seiten.
- Volker Bialas: Erdgestalt, Kosmologie und Weltanschauung. Die Geschichte der Geodäsie als Teil der Kulturgeschichte der Menschheit. Verlag Konrad Wittwer, Stuttgart 1982, ISBN 9783879191352.
- Karl-Eugen Kurrer: Besprechung des Buches von Bialas in Das Argument, Nr. 154, 1985, S. 885–887. PDF
Weblinks
- High precision Geoid determination using heterogeneous Data (N. Kühtreiber, TU Graz) (Memento vom 21. August 2010 im Internet Archive) (PDF-Datei; 1,56 MB)
- Lokale Bestimmung des Geoids aus terrestr.Gradiometermessungen (TU Freiberg) (PDF-Datei)
- Geoid computations based on Torsion balance measurements (TU Budapest) (PDF-Datei; 589 kB)
- Torben Schüler: Berechnung der topografischen Anteile von Lotabweichungen. Archiviert vom Original am 30. September 2007; abgerufen am 15. Juli 2016.