Theodolit
Ein Theodolit ist ein Winkelmessinstrument, das in der Geodäsie (Vermessungskunde) zur Messung von Horizontalrichtungen und Zenit- oder Vertikalwinkeln Verwendung findet. Hierzu wird er mittels eines Stativs lotrecht über einem Punkt aufgestellt. Eine Sonderform ist der Hängetheodolit, der im Bergbau eingesetzt wird.
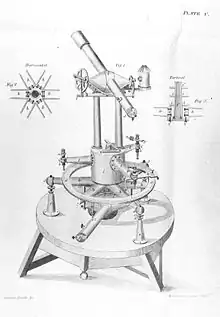




Im Wesentlichen besteht ein Theodolit aus einem Gehäuse, dem Zielfernrohr, einem Vertikal- und einem Horizontal-Teilkreis und ein bis zwei Libellen. Letztere dienen zur lotrechten Ausrichtung der Drehachse (Horizontierung).
In das Zielfernrohr ist ein Strichkreuz integriert, mit dem das Ziel anvisiert wird. Meist werden die dabei eingestellten Winkel in der Einheit Gon vom Gerät angezeigt und/oder gespeichert (100 Gon = 90°).
Etymologie
Die Herkunft des Wortes Theodolit ist ungewiss. Möglicherweise ist es durch Verschmelzung des arabischen alhidate mit englisch the entstanden.[1] Hingegen meint Engelsberger 1969 in seiner Dissertation Beitrag zur Entwicklungsgeschichte des Theodolits, wie kurz zuvor Peters im Beitrag Zur Geschichte und Bedeutung des Wortes Theodolit, dass der Begriff aus dem Griechischen stammt, vom Engländer Leonard Digges in einer alten Schrift gefunden und zum ersten Mal in diesem Zusammenhang benutzt wurde.[2] Diese Erklärung scheint auch naheliegend, denn die drei altgriechischen Begriffe theós (θεός ‚Gott‘), dõron (δῶρον ‚Geschenk‘) sowie lithos (λίθος ‚Stein‘) sind hier vereint.
Bauweise
Messprinzip
Durch Drehen und Kippen des Messfernrohres misst der Theodolit horizontale Richtungen (Drehung um seine vertikale Stehachse) und Vertikalwinkel (Drehung um die horizontale Kippachse). Die Winkel werden meist in Gon ausgegeben, bei älteren Instrumenten auch in Grad (360° = 400 Gon). Zu jeder Drehachse gehört eine Klemmung und eine Feinbewegung.
Manche Geräte geben statt des Zenitwinkels die Steigung in Prozent an. Bei der Artillerie wird ein Theodolit Richtkreis genannt und ist statt in 400 Gon in 6400 Strich geteilt.
Vorläufer der Theodolite waren die Dioptra (Antike), der Azimutalquadrant (um 1500) und die Kippregel. Genaue Universalinstrumente wurden ab 1850 für Triangulation und Astronomie gebaut. Beim Repetitionstheodolit ließ sich durch Addition von Winkeln die Messgenauigkeit erhöhen. Tachymeter erlaubten die Entfernungsmessung an Kurven im Gesichtsfeld – was heute mit Laser und Elektronik erfolgt.
Anallaktisches Fernrohr
Für das Messfernrohr kommen mehrere Bauweisen in Betracht (siehe unten). Bedingung für alle Typen ist ein anallaktisches Fernrohr, bei dem der Brennpunkt des Objektivs, der anallaktische Punkt (Bezugspunkt für die Winkel- und Entfernungsmessung) genau über der Stehachse des Theodolits liegt.
Erstmals hat dies der italienische Ingenieur Ignazio Porro um 1860 durch den Einbau einer Sammellinse zwischen Objektiv und Fadenkreuz erreicht. Sie wird heute in der Regel auch als Fokussierlinse verwendet, wodurch statt des früheren Okularauszugs die Innenfokussierung und ein völlig geschlossenes, staubdichtes Fernrohr möglich wird.
Unter den optischen Systemen überwog bis in die 1960er-Jahre das astronomische Fernrohr, dessen umgekehrtes Bild allerdings für unerfahrene Beobachter störend war. Mit einem am Okular aufgesteckten Umlenkprisma erhielt man ein aufrechtes, aber seitenverkehrtes Bild. Statt der Porrolinse (die mit der Augenlinse ein Huygens-Okular bildet) diente eine Fokussierlinse als Umkehrsystem und machte das astronomische zu einem terrestrischen Fernrohr. Diese Bauart wurde seit den Konstruktionen Heinrich Wilds zur häufigsten.
Für Sonderzwecke (Militär, Satellitenteleskope) werden auch Umkehrprismen wie beim Feldstecher eingebaut. Die Astronomie arbeitet auch mit gebrochenen Fernrohren, die seitlich an der Kippachse montiert sind und bis in den Zenit schwenkbar sind.
Unterbau und Horizontalkreis
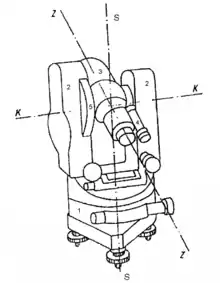
Der Theodolitunterbau oder Limbus enthält den Horizontalkreis (1) und die Vertikalachse (Stehachse) (S). Er trägt die Alhidade (arab.), den Oberbau bestehend aus zwei Stützen (2), der horizontalen Kippachse (K), dem Fernrohr (3), der Kreisablesung (4) und dem Vertikalkreis (5). Das Fernrohr hat ein Strichkreuz (Strichplatte im Okular), durch welches die Zielachse (Z) definiert ist, und eine Innenlinse zum Fokussieren (Scharfstellen).
Der Unterbau sitzt auf der Grundplatte, welche am Stativ aufgesetzt und mit drei Fußschrauben und Libelle horizontiert wird. Die Zentrierung über dem Messpunkt erfolgt durch Verschieben des Instruments am waagrechten Stativteller, anschließend wird die Herzschraube des Stativs von unten her fest angezogen.
Genauigkeitsklassen
Je nach Messgenauigkeit und Einsatzzweck wird unterschieden zwischen
- Bautheodolit (robust und leicht, ca. ±10")
- Tachymeter (inkl. Entfernungsmessung, seit ungefähr 1990 meist digitale Ablesung und automatische Neigungskompensation der Stehachse)
- Präzisions- oder Sekundentheodolit (±1", für Ingenieurgeodäsie)
- und das Universalinstrument (±0.1", z. B. DKM3 und Wild T4) für die Astrogeodäsie.
- Dem Theodolit ähnlich gebaut sind auch manche Passageninstrumente und Sondergeräte für Militär- und Satellitengeodäsie (z. B. das Moonwatch-Apogee oder die früheren Kinetheodolite).
Mögliche Instrumentenfehler
Die vier wesentlichen Instrumentenfehler (Justier- bzw. Fertigungsungenauigkeit, Abweichungen vom theoretischen Idealzustand) bei Theodoliten sind
- Zielachsenfehler: Die optische Achse des Fernrohrs steht nicht senkrecht zur Kippachse des Fernrohrs.
- Kippachsenfehler: Die Kippachse des Fernrohrs steht nicht senkrecht zur Stehachse des Theodolits.
- Höhenindexfehler: Die Nullmarke des Vertikalkreises zeigt bei horizontiertem Theodolit nicht zum Zenit. Liegt kein Höhenindexfehler vor, so entspricht die Zenitrichtung einem Schenkel des Zenitwinkels. Der andere Schenkel zeigt in Richtung des Beobachtungszieles.
- Kreisteilungsfehler: Die Skalenteilung auf den Teilkreisen weicht in der Regel unsystematisch vom Ideal gleichmäßiger Teilung ab.
Instrumentenfehler (feinmechanisch) lassen sich durch
- Messungen in zwei Fernrohrlagen und Mittelwertbildung eliminieren,
- wiederholtes Messen mit verschiedenen Teilkreisstellungen minimieren,
- nachträgliche Reduktion rechnerisch eliminieren oder im Einfluss reduzieren und/oder
- hohe optisch-mechanische Präzision (mindestens 1 µm) im Einfluss minimieren.
Weitere kleine Einflüsse wie thermische Effekte oder mechanische Restspannungen im Theodolitaufbau bleiben i.a. unter 1" und sind damit vernachlässigbar.
Nicht gänzlich eliminierbar ist hingegen der Stehachsfehler. Er liegt vor, wenn die Stehachse nicht parallel zur Richtung der Schwerkraft liegt. Dann ist die Horizontierung fehlerhaft. Ein Grund dafür kann eine Dejustage der zur Horizontierung genutzten Instrumente sein. Der Stehachsfehler ist ein Bedienungs- oder Aufstellfehler. Eine verbleibende Restneigung der Stehachse zur Lotrichtung kann durch einen zweiachsigen Neigungssensor bei modernen Tachymetern intern gemessen und automatisch in die Messergebnisse eingebracht werden.
Die Stehachse ist rechtwinklig zu den Libellenachsen beziehungsweise zu mehreren Messrichtungen. Die Zielachse ist rechtwinklig zur Kippachse. Die Kippachse ist rechtwinklig zur Stehachse. Alle drei Achsen schneiden sich idealerweise in einem Punkt.
Richtungsmessung mit Theodolit oder Tachymeter
Messgrößen
Mit einem Theodolit können folgende Messgrößen beobachtet werden:
- Horizontalwinkel – als Differenz der Richtungsbeobachtungen zu zwei Zielen,
- Vertikalwinkel: meist als Zenitdistanz (vom Zenit zum Messpunkt), seltener als Höhenwinkel über dem Horizont
- Winkeldifferenzen: zur Entfernungsmessung mit den zwei Distanzfäden (Reichenbachfäden) oder mit Reduktionstachymetern
- Messung mit beweglichem Fadennetz: nur bei speziellen Theodoliten für die Astrogeodäsie, siehe unpersönliches Mikrometer.
- Elektronische Distanzmessung: fast alle modernen Theodolite und Tachymeter sind zusätzlich mit einem Laserentfernungsmesser ausgestattet.
Aufstellung und Richtungsmessung
Vor den Messungen ist das Instrument auf dem Stativ genau zu horizontieren und meistens zentrisch über einem Bodenpunkt (Vermessungs- oder Messpunkt) aufzustellen. Die Horizontierung mit der Alhidaden-Libelle bewirkt, dass die Stehachse des Instrumentes mit der Lotrichtung zusammenfällt.
- Zentrierung und Horizontierung werden gleichzeitig nach einem besonderen, schematisierten Vorgehen durchgeführt: entweder mit einem Senklot, das in die Rändelschraube (Herzschraube) des Stativtellers eingehängt wird, oder ein im Dreifuß oder Theodolit integriertes optisches Lot.
- Nun werden mit dem dreh- und kippbaren Messfernrohr (Fernrohr mit Fadenkreuz – heute: Strichkreuz) nacheinander alle einzumessenden Punkte anvisiert -- als erstes meist die Polygonpunkte, anschließend alle Detailpunkte.
- Nach jeder Zielung wird die Richtung am Teilkreis (im Theodolit feststehende Winkelskala) abgelesen, bei zusätzlicher Höhenmessung auch der Zenitwinkel. Klassische Theodolite haben hierfür ein Ablesemikroskop, in das beide Winkelstellungen eingespiegelt werden.
- Bei elektronischen Theodoliten und Tachymetern werden die Teilkreise durch Inkremental- oder Absolutwertgeber automatisch abgetastet, die Winkelwerte durch A/D-Wandler in Ziffern umgewandelt, angezeigt und gespeichert.
Ablesung der Teilkreise
Die Vorteile der automatischen Teilkreisablesung bestehen darin, dass die Messung um 20–50 % rascher wird, weniger ermüdet und persönliche Ablesefehler entfallen; auch Irrtümer bei der Datenerfassung werden seltener. Doch ist auf exakte Codierung der Messpunkte zu achten, damit später die digitale Weiterverarbeitung reibungslos ablaufen kann.
Zur automatischen Erfassung wird der Teilkreis codiert und mit unterschiedlichen Techniken abgetastet (optoelektronisch, elektrisch, magnetisch). Die magneto-elektronische Abtastung ist auch als Inductosyn bekannt. Elektrische Abtastungen sind heute technisch veraltet. Weit verbreitet sind hingegen optisch-elektronische Abtastverfahren, bei denen zwischen Durchlicht- und Auflichttechnik unterschieden wird.
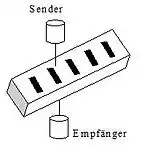
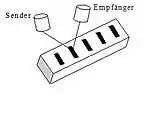
Beim Durchlichtverfahren wird mittels Schwärzung codiert, wodurch lichtdurchlässige und lichtundurchlässige Bereiche entstehen. Die Codierung wird von einer Seite beleuchtet, auf der anderen Seite sitzt eine Fotodiode als Empfänger. Beim Auflichtverfahren sind Sender und Empfänger auf der gleichen Seite angeordnet. Da der Teilkreis unterschiedliche Reflexionseigenschaften aufweist, müssen verschieden starke Lichtstrahlen registrierbar sein. Die Codierscheiben werden üblicherweise mit einem Gray-Code versehen.
Der Winkel zwischen zwei Zielpunkten bezüglich des Instrumentenstandpunkts errechnet sich nun aus der Differenz der zwei gemessenen Richtungen.
Bezugsrichtungen
Während sich die Ablesungen am Vertikalkreis auf den Zenit bzw. Horizont beziehen, kann die Messung der Horizontalwinkel verschiedene Bezugsrichtungen haben:
- die Richtung zu einem beliebigen Zielpunkt (z. B. der nächstgelegene Polygonpunkt oder ein gut sichtbares Fernziel)
- die Richtung zu einem amtlichen Festpunkt, dessen Koordinaten bekannt sind: ein Trigonometrischer Punkt (TP), ein Aufnahmepunkt (AP) oder ein Einschaltpunkt (EP). Es kann dann aufs geodätische Koordinatensystem (Gitternord) orientiert werden
- Orientierte Richtung: nach magnetisch, geografisch- oder Gitter-Nord. Bei ersteren ist eine Korrektur anzubringen, bei Gitternord werden aus allen gemessenen Richtungen geodätisch korrekte Richtungswinkel.
Die Bezugsrichtung der Vertikalwinkel ist bei korrekter Horizontierung die Lotrichtung und muss daher i. d. R. nicht korrigiert werden. Ausnahmen sind schlecht kalibrierte Instrumente (Horizontschräge) und in Spezialfällen die Lotabweichung. Bei horizontal ausgerichtetem Messfernrohr beträgt der Zenitwinkel genau 100 Gon (90°), was auch Nivellierblick genannt wird.
Beobachtung und Genauigkeit
Zur Fehlereliminierung werden die Ziele in einem Satz gemessen (manchmal auch in Halbsätzen). Ein Satz besteht dabei aus zwei Messreihen (2 Halbsätzen), wobei für die zweite Messreihe das Fernrohr durchgeschlagen (um die Kippachse zur anderen Geräteseite gedreht), der Oberbau um 200 Gon (180°) gedreht wird und die Ziele erneut anvisiert werden. Dadurch erfolgen die Ablesungen der Zielrichtungen an diametral gegenüberliegenden Stellen auf dem Horizontalkreis und an korrespondierenden Stellen auf dem Vertikalkreis. Die Einflüsse des Ziel-, Kippachs- und Höhenindexfehlers haben in beiden Fernrohrlagen den gleichen Betrag, aber ein entgegengesetztes Vorzeichen. Bei der Mittelbildung der Horizontalrichtung und der Zenitwinkel aus beiden Fernrohrlagen erhält man so Beobachtungen, die frei von den Einflüssen der Achsfehler sind. Die Genauigkeit liegt dadurch bei 0,01 mgon bis 1 cgon Standardabweichung.[3]
Bekannte Hersteller

- F.W. Breithaupt & Sohn
- Geo-Fennel (früher Fennel)
- Trimble Navigation:
- Carl Zeiss (historisch), in Trimble Navigation aufgegangen
- Geodimeter (historisch), in Trimble Navigation aufgegangen
- Leica Geosystems:
- Kern & Co (bis 1992, dann in Leica Geosystems aufgegangen)
- Wild Heerbrugg (historisch), 1990 in Leica Geosystems aufgegangen
- Topcon
- Sokkia
Einige frühere Hersteller:
- Dennert & Pape Aristo – Werke (bis ca. 1998)
- Starke & Kammerer, Wien (bis ca. 1950)
- Miller, Innsbruck (bis ca. 1990)
- Zeiss Jena (bis ca. 1995)
- FPM-Holding (ehemals VEB Freiberger Präzisionsmechanik)
Siehe auch: Hersteller von Tachymetern
_1981%252C_MiNr_641.jpg.webp) Theodolit, um 1810, auf einer Berliner Wohlfahrtsmarke von 1981
Theodolit, um 1810, auf einer Berliner Wohlfahrtsmarke von 1981 sowjetischer Artillerie-Richtkreis „PAB-2“
sowjetischer Artillerie-Richtkreis „PAB-2“ Sekundentheodolit K1S von Kern & Co AG
Sekundentheodolit K1S von Kern & Co AG Moderner Theodolit von Leica Geosystems
Moderner Theodolit von Leica Geosystems Schultheodolit der Marke Aristo aus den 1950er-Jahren
Schultheodolit der Marke Aristo aus den 1950er-Jahren
Siehe auch
Literatur
- Bertold Witte, Peter Sparla: Vermessungskunde und Grundlagen der Statistik für das Bauwesen. 7. Auflage. Wichmann, Berlin 2011, ISBN 978-3-87907-497-6.
- Heribert Kahmen: Angewandte Geodäsie. Vermessungskunde. 20. Auflage. Walter de Gruyter, Berlin / New York, ISBN 3-11-018464-8.
Weblinks
Einzelnachweise
- Theodolit. In: Lueger: Lexikon der gesamten Technik. zeno.org, abgerufen am 13. November 2018.
- Ralf Kern: Wissenschaftliche Instrumente in ihrer Zeit. Band 4: Perfektion von Optik und Mechanik. König, Köln 2010, ISBN 978-3-86560-868-0, S. 480.
- Heribert Kahme: Angewandte Geodäsie: Vermessungskunde. 20. Auflage. Walter de Gruyter, Berlin 2006, ISBN 978-3-11-018464-8, S. 97–98 (Google Books).