Niveaufläche
Als Niveaufläche wird in den Geowissenschaften eine Äquipotentialfläche des Schwerepotentials bezeichnet. Auf der Erde sind Niveauflächen annähernd parallel zum Meeresspiegel und sind die ∞¹-mannigfaltige Schar jener Flächen, die überall senkrecht auf der örtliche Lotrichtung stehen.
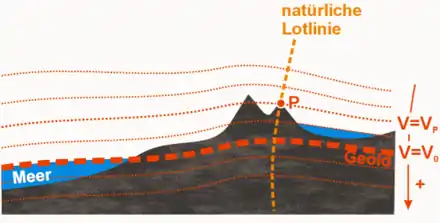
Die Niveaufläche im mittleren Meeresniveau wird Geoid genannt.
Die Potentialtheorie definiert die Niveauflächen als jene Flächen eines konservativen Kraftfeldes, auf denen die potentielle Energie konstant ist. Beim Verschieben eines Körpers (fiktiv einer unendlich kleinen Probemasse) entlang einer Niveaufläche muss – von Reibungsverlusten abgesehen – keine physikalische Arbeit verrichtet werden.
Die Physik verwendet den Begriff Niveaufläche auch für andere Kraftfelder, z. B. für Magnetfelder oder elektrische Felder.
Geodäsie und Ozeanografie
Die Geodäsie definiert den physikalischen Höhenbegriff durch den senkrechten Abstand zweier Niveauflächen. Die Höhendifferenz ΔH zweier Punkte ist die Potentialdifferenz ΔV ihrer Niveauflächen (siehe Bild) dividiert durch den Betrag der lokalen Erdbeschleunigung g:
- ΔH = H2 - H1 = ( V2 - V1 ) / g ,
wobei g vom Erdäquator bis zu den Polen wegen der Schwereabplattung von etwa 9,7803 m/s² auf 9,8322 m/s² zunimmt. Deshalb und wegen der geologisch bedingten Lotabweichungen sind die Niveauflächen auch nicht völlig parallel. Jene in mittlerer Meereshöhe wird Geoid genannt und ist die Bezugsfläche für die in Technik und Alltag verwendeten geometrischen Gebrauchshöhen (siehe auch orthometrische Höhe).
Die Ozeanografie benutzt diese durch Höhe Null ausgezeichnete Niveaufläche, um aus den Abweichungen zwischen ihr und dem wahren Meeresspiegel beständige Meeresströmungen und Winde zu modellieren. Die Meereshöhen- und Geoidbestimmung auf den Ozeanen erfolgt großteils durch Satellitenaltimetrie, derzeit unter anderem durch die ESA-Sonde GOCE.
Siehe auch
Literatur
- Wolfgang Torge, Geodäsie, Sammlung Göschen Band 2163, De Gruyter-Verlag 1975.
- B. Hofmann-Wellenhof, Helmut Moritz: Physical Geodesy, ISBN 3-211-23584-1, Springer-Verlag, Wien 2006.