Astrogeoid
Als Astrogeoid wird eine Geoidbestimmung mit astro-geodätischen Messdaten bezeichnet. Sie beruht in ihrer klassischen Version auf einer profilartigen oder flächenhaften Integration von gemessenen Lotabweichungen. Als Vorgänger der Methodik sind die im 18.–19. Jahrhundert durchgeführten genauen Gradmessungen zur Bestimmung der theoretischen Erdfigur anzusehen.
Die Methodik wird auch „Astronomisches Nivellement“ genannt, weil sie ein Analogon zum trigonometrischen Nivellement darstellt, bei der die astronomisch gemessene Lotrichtung die Rolle des Höhenwinkels übernimmt. Die Theorie wurde bereits vor 130 Jahren (vom deutschen Geodäten Friedrich Robert Helmert) entwickelt und geht in ihren Grundzügen auf Carl Friedrich Gauß zurück.
Ihre erste zufriedenstellende Anwendung (im Harz und in Österreich) gelang aber erst zu Beginn des 20. Jahrhunderts mit der Entwicklung praktikabler Messmethoden der Astrogeodäsie. Bis heute ist sie die genaueste Methode zur Geoidbestimmung auf dem Festland, die einige mm bis cm erreichen kann. Bei Projekten der Landesvermessung wird sie heute zunehmend mit der Gravimetrie kombiniert, während auf den Ozeanen die Verfahren der Satellitengeodäsie den Vorrang genießen.
Eine dem Astro-Geoid verwandte Geoidbestimmung ist die mit Schweregradienten. In einigen Ländern (z. B. Ungarn) laufen Versuche, das zu dünne Lotabweichungsnetz mit Drehwaagen-Messungen der Erdölexploration oder mit Gradiometrie zu kombinieren (siehe Weblinks).
Lotabweichung und Geoid
Das Geoid ist jene Niveaufläche der Erde, die mit dem mittleren Meeresspiegel der Weltmeere zusammenfällt. Als idealisierte Form der Erdoberfläche stellt sie für die Geowissenschaften die „theoretische Erdfigur“ dar und dient als Bezugsfläche für fast alle Höhenmessungen. Daher ist ihre genaue Bestimmung auch von höchster praktischer Bedeutung.
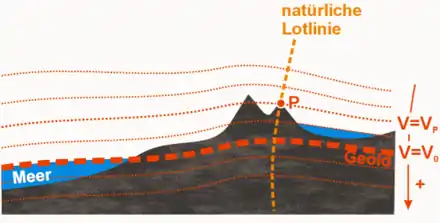
Die Lotabweichung ist die Abweichung des wahren Lotes von der Normalen einer mathematischen Referenzfläche, wofür in der Regel ein regionales oder globales Erdellipsoid herangezogen wird. Die Differenz zwischen der ermittelten astronomischen Breite φ bzw. Länge λ und der Ellipsoidnormalen (geodätische Breite B und Länge L) wird in den zwei Komponenten
- ξ = φ − B
- η = (λ − L).cos φ
angegeben. Diese Nord-Süd- bzw. Ost-West-Komponenten der Lotabweichung können – je nach dem Aufwand bei der Messung – auf 0,1″ bis 0,3″ genau bestimmt werden.
Die Größen φ und λ stellen den Richtungsvektor des Zenits (= wahre Lotrichtung) dar, der als Durchstoßpunkt der örtlichen Vertikalen mit der Himmelskugel beobachtet wird. Er ergibt sich aus der genauen Messung von Sterndurchgängen oder von Aufnahmen mit einer Zenitkamera – zunächst im System der Sternörter, die anschließend in geografische Koordinaten umgerechnet werden.
Die Größen B und L der Messpunkte ergeben sich andererseits aus dem terrestrischen Vermessungsnetz, dessen Gauß-Krüger-Koordinaten in Breiten- und Längenwinkel am Referenzellipsoid umgerechnet werden. Die Lotabweichung (ξ, η) bezieht sich i.a. auf dieses Referenzellipsoid und seinen Fundamentalpunkt, der meist nahe der Landesmitte liegt. Sie wird deshalb auch relative Lotabweichung genannt.
Wenn die Landesvermessung hingegen nicht regional, sondern auf das mittlere Erdellipsoid bezogen ist (z. B. bei einer GPS-Vermessung), so erhält man die Lotabweichung (ξ, η) dementsprechend in einem Weltsystem, beispielsweise dem WGS84. Sie wird dann absolut genannt.
Die Lotrichtung steht überall senkrecht auf dem Geoid, da dieses die perfekte Horizontale im Niveau des Meeresspiegels darstellt. Hätte die Erde keine Erhebungen und wäre auch im Erdinnern völlig regelmäßig aufgebaut, so wären alle Lotabweichungen Null und das Geoid identisch mit dem Erdellipsoid.
Integration der Lotabweichung
Jede Lotrichtung gibt einen Hinweis auf die kleinen Unregelmäßigkeiten des Schwerefeldes und resultiert aus der störenden Anziehung der Berge und Täler und ihrer etwas veränderlichen Dichte. Der Einfluss des Geländes macht in den Gebirgen Europas bis zu 50" aus, jener der Geologie etwa 5–10". Dies übertrifft die moderne geodätische Messgenauigkeit um mindestens das Zehnfache, sodass sie heutzutage bei jeder genauen Vermessung zu berücksichtigen ist. Auf Ebenen und im Hügelland variiert die Lotabweichung hingegen nur um etwa 5 Winkelsekunden.
Zur Geoidbestimmung benötigt man nicht nur die Werte ξ, η auf den Messpunkten (die je nach Land etwa 10 bis 50 km auseinanderliegen), sondern auch ihren Verlauf dazwischen. Früher hat man sie einfach gemittelt und das Geoid bestenfalls mit Dezimetergenauigkeit erhalten. Heute werden hingegen Methoden der „topografischen Interpolation“ angewendet, bei denen man den Einfluss der Berge zunächst „wegrechnet“ (topografische Reduktion). Die geglätteten ξ-η-Werte werden nun in kleinen Schritten entlang der Profile interpoliert und das Gelände rechnerisch wieder „aufgesetzt“. Mit diesem Remove-Restore-Prozess erhält man im ganzen künftigen Geoidnetz die genäherten Lotabweichungen auch dort, wo man sie gar nicht gemessen hat.
Im letzten Schritt werden diese gerechneten Lotabweichungen entlang aller Profile integriert, das heißt mit der jeweiligen Wegstrecke multipliziert. Durch Summation – wie beim Nivellement – erhält man so in einem flächenhaften Raster die Höhenunterschiede des Geoids zum Erdellipsoid, womit die Geoidbestimmung abgeschlossen ist.
Kombinierte Verfahren
Durch eine Kombination verschiedener Messdaten steigt im Allgemeinen die Genauigkeit und die Verlässlichkeit, aber auch der Aufwand. Besonders wirksam sind Kombinationslösungen, wo sich methodische Schwächen und Stärken paaren.
So kann die Gravimetrie oder eine Vernetzung mit GPS-Messungen eine gute Höhenlage des Geoids liefern, während das Astrogeoid seine Neigung am besten erfasst. Die entsprechenden Kombinationen heißen astro-gravimetrische Geoidbestimmung bzw. GPS-Nivellement. Einige Projekte in Gebirgsländern zielen auch auf die Einbeziehung gemessener Höhenwinkel, wofür unter anderem die Namen L. Hradilek (CZ) und E. Grafarend (D) stehen.
Geoidlösungen durch Kombination von Lotabweichungs- und Geländedaten wurden früher „astro-topografisch“ genannt, sind aber heute durch die digitalen Geländemodelle zum Standard geworden. Beispiel ist die oben genannte topografische Reduktion.
Auch globale Potentialmodelle der Erde lassen sich gut mit gravimetrischen oder Astrogeoiden kombinieren, weil sie bei der Reduktion den regionalen Trend der Messdaten korrigieren können. Solche harmonischen Kugelfunktions-Modelle werden seit den Arbeiten von R.H. Rapp und H.G. Wenzel aus der Kombination von Satellitengeodäsie mit terrestrischer bzw. Fluggravimetrie gewonnen. Sie sind heute schon bis zu Grad und Ordnung 720 oder 1000 möglich, was einer Auflösung von 20 bis 30 km entspricht.
Für das ozeanische Geoid ist die Satellitenaltimetrie mit Radar die wichtigste Datenquelle, weil die Bahnhöhen direkt über dem Meeresspiegel gemessen werden. Wegen der Meeresströmungen und Gezeiten, die 1–2 Höhenmeter ausmachen können, sind hier Datenmodelle der Ozeanografie erforderlich, die ihrerseits durch die Geodäsie an Crossing Points der Satellitenspuren abgesichert werden.
Sehr erfolgversprechende Entwicklungen der Satellitentechnik sind die Gradiometrie und das SST, mit denen die Spezialsatelliten GRACE und GOCE Änderungen des Geoids auf wenige Zentimeter erfassen sollen. Langfristige Änderungen im Erdschwerefeld werden so erfassbar, doch beträgt die räumliche Auflösung erst etwa 200 Kilometer. Hier ist eine Kombination mit detailreicheren Methoden unerlässlich.
Globale und regionale Geoidbestimmung
... ...
Geschichte der astro-geodätischen Geoidbestimmung
- 19. Jahrhundert: Gauß, J. B. Listing, Helmert, Testfeld Harz, E.Galle, Fundamental- und Laplacepunkte
- Bis 1960: St.-Gotthard-Profil, J. Litschauer und W. Wolf, Europanetz und ED50, Vening-Meinesz (Isostasie) und Hayford-Ellipsoid, Mercury-Geoid und USCGS (Irene Fischer)
- Ab 1970: Europäisches Datum 1979, J. Levallois, Hohe Tatra (Hradilek), Testnetze IFE Hannover (Institut für Erdmessung) und Wien, Kollokation (Hans Sünkel, Christian Tscherning et al.), FK5, GPS-Levelling, Schweizer Geoid, Rheingraben und Nördlinger Ries, European Gravimetric Geoid (EGG), Argentinien, Türkei, Zenitkameras, HR und SK, Marcel Mojzeš, Geoidprojekte der Central European Initiative (CEI)
- Gravimetrische und Kombinationslösungen: Tanni-Geoid, Bomford-, SAO-Netz, Y. Kozai, Satellitentriangulation, H. H. Schmid (Weltnetz der Satellitentriangulation), W. Torge und H. Denker vom IFE Hannover, Austrian Geoid 2000, Satellit GFZ-1 und Potsdamer Geoid, GeoLIS und geologische Datenbanken, Geodesy beyond 2000, Internationale Geoid-Kommission, GRACE, GOCE.
Siehe auch
Literatur
- Gottfried Gerstbach: Regionale Geoidbestimmung. In: Kolloquium der Assistenten der Studienrichtung. Vermessungswesen 1974–1976 (= Geowissenschaftliche Mitteilungen. Bd. 11, ISSN 1811-8380). Institut für Photogrammetrie Technische Universität Wien, Wien 1975.
- Siegfried Heitz: Geoidbestimmung durch Interpolation nach kleinsten Quadraten aufgrund gemessener und interpolierter Lotabweichungen (= Deutsche Geodätische Kommission bei der Bayerischen Akademie der Wissenschaften. Veröffentlichungen. Reihe: C. Bd. 124, ISSN 0065-5325). Verlag der Bayerischen Akademie der Wissenschaften, München 1968 (Zugleich: Bonn, Hab.-Schrift).
- Karl Ledersteger: Astronomische und Physikalische Geodäsie (Erdmessung) (= Handbuch der Vermessungskunde. Band 5). 10., völlig neu bearbeitete und neu gegliederte Auflage. J. B. Metzler, Stuttgart 1969, Kapitel 4 (Lotabw./Geoidbestimmung), 7 (Kugelfunktionen) und 12/13 (Geoidundulationen, Molodenskij, Weltsystem).
- Fernando Sansò, Michael Sideris (Hrsg.): Geoid Determination Theory and Methods (= Lecture Notes in Earth Sciences. Bd. 110). Springer, Berlin 2007, ISBN 978-0-387-46386-5.
Weblinks
- Das astro-gravimetr. Geoid der Schweiz (CHGeo2004)
- Geoid aus Lotabweichungen (Astro/Physikal.Geodäsie, TU München)
- High precision Geoid determination using Astro & Gravimetric Data (TU Graz) (Memento vom 21. August 2010 im Internet Archive) (PDF; 1,56 MB)
- Astrogeoid or gravimetric geoid - that is the question (TU Wien) (PDF; 16 kB)
- Lokale Bestimmung des Geoids aus terrestr.Gradiometermessungen (TU Freiberg) (PDF-Datei)
- Geoid computations based on Torsion balance measurements (TU Budapest) (PDF; 589 kB)