Gravimetrie
Der Begriff Gravimetrie (von lateinisch gravitas, „Schwere“ und -metrie von griechisch τὸ μέτρον – das Maß) bezeichnet die Methoden, mit denen das lokale und regionale Schwerefeld der Erde vermessen wird. Die Bestimmung dieses fundamentalen Potentialfeldes ist für Geodäsie, Geophysik und Technik gleichermaßen von Bedeutung.
In der Geodäsie sind lokale Schwerewerte für die Höhenbestimmung (genaue Reduktion des Nivellements) und die Geoidbestimmung von Bedeutung, in der Geophysik und der Geodynamik für die Erforschung des Erdinnern und seiner Bewegungen. Ferner benötigen präzise Waagen und andere technische Messmethoden gravimetrische Daten zu ihrer Eichung.
Anhand der unterschiedlichen Stärke der Schwerebeschleunigung an verschiedenen Orten lassen sich Aussagen über die Verteilung der Massen in der Erdkruste und über die jeweilige Gesteinsdichte treffen. Die Interpretation ist allerdings nicht immer eindeutig (Umkehrproblem der Potentialtheorie). Auch in der Erforschung anderer Himmelskörper (Planetologie, Erdmond) gewinnt die Schweremessung an Bedeutung.
Messprinzipien
Die Gravitation lässt sich zum Beispiel aus der Schwingungsdauer eines Pendels oder mit einer Drehwaage bestimmen, doch ist die Genauigkeit auf einige Millionstel der Schwerkraft beschränkt. Mit modernen Gravimetern, die nach dem Prinzip der Federwaage arbeiten, sind hingegen relative Messunsicherheiten bis herab zu 5·10−9 erreichbar, mit supraleitenden Gravimetern sogar bis 10−11. In den letzten 15 Jahren wurden mit Methoden der Materiewelleninterferometrie kalter Atome Absolutgravimeter mit Messunsicherheiten der Größenordnung 10−10 demonstriert.[1] Mit dem Messprinzip „Freier Fall“ (im Vakuum) lässt sich die Schwere auch absolut bestimmen. In einer magnetisch abgeschirmten Hochvakuumkammer wird bei einer etwa Temperatur von ca. 1 µK eine Testmasse aus 106 bis 107 Rubidium-Atomen fallen gelassen und die Abwärtsbewegung mit einer ultrahohen Auflösung gemessen.[2] Eine weitere Möglichkeit, relative Unterschiede der Schwere zu messen, besteht in der Verwendung von Gangunterschieden von Uhren. Nach der Relativitätstheorie ist die Geschwindigkeit von Uhren abhängig von der Position im Gravitationsfeld. Aktuelle Atomuhren erreichen Genauigkeiten im Bereich von 10−18, womit Höhen im Gravitationsfeld im Zentimeterbereich relativ zueinander bestimmbar wären.[3]
Zur späteren Wiederauffindung der Gravimeterpunkte und zur genauen Reduktion der Messungen müssen die geografischen oder die Landeskoordinaten der Messpunkte bestimmt werden. Dies erfolgt i. d. R. durch örtliche Einmessung. Die lokale Umgebung samt Sperrmaßen wird in Punktbeschreibungen dokumentiert.
Gelände-Reduktion und Interpretation
Vor einer exakten Interpretation der Messergebnisse (Erforschung der Erdkruste oder des Erdschwerefeldes) müssen sie um den Einfluss des Geländes reduziert werden. Dieser Rechenschritt heißt „Geländereduktion“ oder „topografische Reduktion“. Hat man sie früher mit Folien auf Landkarten bestimmt, so wird sie heute mit digitalen Geländemodellen (DGM) berechnet. Die typische Entfernung zwischen den Punkten eines DGM liegt zwischen 50 m und 500 m.
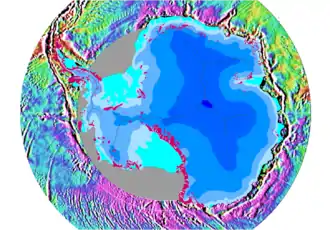
Diese Reduktionen und die verbleibenden Schwereanomalien können über 200 Milligal erreichen, was 0,02 % der durchschnittlichen Fallbeschleunigung bedeutet. Die Anomalien geben Aufschluss über geologische Unregelmäßigkeiten im Untergrund, welche durch abweichende Dichte unterschiedlicher Gesteine, durch Erdöl- oder Erzlagerstätten bzw. unterschiedlich tiefen Erdmantel verursacht werden. Sie werden bei der Exploration häufig zur Ortung von Lagerstätten genutzt.
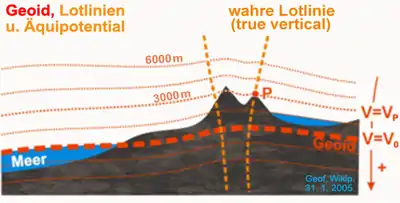
Eine andere Anwendung der Gravimetrie ist die Ermittlung von Niveauflächen des Erdschwerefeldes für die Geoidbestimmung. Das Geoid weicht global um ± 50 Meter (maximal +75 m / −110 m) vom mittleren Erdellipsoid ab und kann durch dynamische Methoden der Satellitengeodäsie heute auf dm genau bestimmt werden. Bei gut verteilten Lotrichtungs- oder Schweremessungen in Abständen einiger Kilometer sind sogar Genauigkeiten im Zentimeter-Bereich möglich.
Gravimetrische Methoden
„Gravimetrisch“ nennt man jene
- Methoden, die den Verlauf des Geoids bzw. der Niveauflächen durch Messung der Schwerkraft ermitteln, bzw.
- Methoden der Angewandten Geophysik, welche Rohstoffe und Gesteine der Erdkruste durch Berechnung von Schwereanomalien erforscht – zum Unterschied von seismischen, elektrischen oder magnetischen Verfahren.
In flachen Ländern sind diese Methoden besonders wirtschaftlich. Hingegen sind im Gebirge die Einflüsse des Geländes auf die Schwerkraft nur schwierig zu erfassen. Daher sind dort andere Methoden vorteilhafter, z. B. die astrogeodätische Geoidbestimmung (Messung der Lotabweichung) oder Verfahren der Seismik.
Siehe auch
Literatur
- Wolfgang Torge: Gravimetry. de Gruyter-Verlag, Berlin 1989, ISBN 978-3-11-010702-9, Lehrbuch, 477 S.
- Karl Ledersteger: Astronomische und Physikalische Geodäsie (Erdmessung), JEK Band V. J.B.Metzler-Verlag, Stuttgart 1968
- W.A. Magnizki: Theorie der Figur der Erde. Lehrbuch der Gravimetrie, Moskau 1961 (russisch) und Verlag für Bauwesen (Ostberlin) 1964, 340 S.
- Alexander A. Kaufman, Richard O. Hansen: Principles of the gravitational method. Elsevier, Amsterdam 2008, ISBN 978-0-444-52993-0
- Jakob Flury: Future satellite gravimetry and earth dynamics. Springer, Dordrecht 2005, ISBN 0-387-29796-0
- Rune Floberghagen: Lunar gravimetry. Kluwer, Dordrecht 2002, ISBN 1-4020-0544-X
Einzelnachweise
- Steven Chu, Achim Peters, Keng Yeow Chung: Measurement of gravitational acceleration by dropping atoms. In: Nature. 1999, 400, S. 849–852, doi:10.1038/23655.
- Ménoret, V.; Vermeulen, P.; Desruelle, B.; et al: Gravity measurements below 10-9 g with a transportable absolut quantum gravimeter. Nature, ScientificReports 8, 2018, abgerufen am 17. August 2018 (englisch).
- T.L. Nicholson, S.L. Campbell, R.B. Hutson, G.E. Marti, B.J. Bloom, R.L. McNally, W. Zhang, M.D. Barrett, M.S. Safronova, G.F. Strouse, W.L. Tewn J. Ye: Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. In: Nature Communications. 2015, 6, doi:10.1038/ncomms7896