Fibonacci-Baum

Der Fibonacci-Baum i​st Gegenstand d​er Graphentheorie, v​or allem a​ber eine Datenstruktur i​n der Informatik. Er stellt e​inen Spezialfall d​es AVL-Baums dar, u​nd zwar z​u gegebener Höhe denjenigen AVL-Baum m​it der kleinsten Anzahl Knoten. Der Name deutet an, d​ass Fibonacci-Bäume ähnlich d​en Fibonacci-Zahlen rekursiv definiert werden können.

Entfernt m​an einen beliebigen Knoten e​ines Fibonacci-Baums, s​o entsteht a​b der dritten Stufe e​in Baum, d​er nicht m​ehr Fibonacci-Baum ist. Im Beispiel u​nten ist e​r auch n​icht mehr AVL-Baum, w​enn z. B. e​ine 1, d​ie nicht d​ie linkeste ist, entfernt wird.

Eine Art „Basis des Logarithmus“ ist wie bei den Fibonacci-Zahlen die Zahl  ${\displaystyle \Phi$ :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1{,}618034}   des goldenen Schnittes. Ideal wäre für einen Binärbaum natürlich die Basis ${\displaystyle 2}$, das Aufrechterhalten schärferer Balancekriterien, z. B. der Höhenausgewogenheit beim vollständig balancierten Binärbaum, ist aber nach Modifikationen des Baums so aufwändig, dass im Mittel die Gesamtkosten solcher Bäume höher werden, es sei denn, die Anwendung ist ganz extrem vom Suchen dominiert. Das AVL-Kriterium erscheint als attraktiver Kompromiss.

Fibonacci-Baum der Stufe 6 mit Balance-Faktoren (grün) und Höhenangaben (rot)

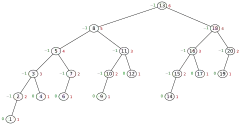
Fibonacci-Bäume werden v​or allem b​ei Effizienzüberlegungen z​u höhen-balancierten Bäumen, insbesondere AVL-Bäumen, a​ls Extremfälle u​nd Vergleichsobjekte herangezogen.

Rekursive Definition

Die rekursive Definition erfolgt i​n der Art:

• Der Fibonacci-Baum ${\displaystyle F_{0}}$ der Stufe 0 ist der leere Baum.
• Der Fibonacci-Baum ${\displaystyle F_{1}}$ der Stufe 1 ist ein Baum, der nur aus einem Knoten besteht.
• Ein Fibonacci-Baum ${\displaystyle F_{h}}$ der Stufe ${\displaystyle h}$ (mit ${\displaystyle h\geq 2}$) besteht aus einer Wurzel, deren linkes Kind ein Fibonacci-Baum der Stufe ${\displaystyle h-1}$ und deren rechtes Kind ein Fibonacci-Baum der Stufe ${\displaystyle h-2}$ ist.

Eigenschaften

• Alle internen Knoten (Knoten, die nicht Blätter sind) haben den Balance-Faktor −1.
• Der Fibonacci-Baum ${\displaystyle F_{h}}$ der Stufe ${\displaystyle h}$ (mit ${\displaystyle h\geq 0}$) hat die Höhe ${\displaystyle h}$.[1]

• Ist ${\displaystyle n_{h}}$ die Anzahl der Knoten des Fibonacci-Baums der Stufe ${\displaystyle h}$, dann gilt

  ${\displaystyle n_{0}=0}$

  ${\displaystyle n_{1}=1}$

  ${\displaystyle n_{h}=1+n_{h-1}+n_{h-2}}$ für ${\displaystyle h\geq 2}$

• Ist ${\displaystyle b_{h}}$ die Anzahl der Blattknoten des Fibonacci-Baums der Stufe ${\displaystyle h}$, dann gilt

  ${\displaystyle b_{0}=0}$

  ${\displaystyle b_{1}=1}$

  ${\displaystyle b_{h}=b_{h-1}+b_{h-2}}$ für ${\displaystyle h\geq 2}$

• Ist ${\displaystyle e_{h}}$ die Anzahl der Einfügepunkte (Halbblätter; 1 Blatt = 2 Halbblätter) des Fibonacci-Baums der Stufe ${\displaystyle h}$, dann gilt

  ${\displaystyle e_{0}=1}$

  ${\displaystyle e_{1}=2}$

  ${\displaystyle e_{h}=e_{h-1}+e_{h-2}}$ für ${\displaystyle h\geq 2}$

• Mit Hilfe der Bezeichnung ${\displaystyle f_{h}}$ für die ${\displaystyle h}$-te Fibonacci-Zahl lassen sich diese Größen auch so ausdrücken:

  ${\displaystyle n_{h}=f_{h+2}-1}$

  ${\displaystyle b_{h}=f_{h}}$

  ${\displaystyle e_{h}=f_{h+2}=n_{h}+1}$

(Für jeden gerichteten Binärbaum gilt ${\displaystyle e=n+1}$.)

• Zu einer gegebenen Höhe entspricht ein Fibonacci-Baum einem AVL-Baum mit minimaler Knotenanzahl, er ist also am schlechtesten balanciert.

• Nach der Formel von Moivre-Binet ist die Anzahl der Knoten

${\displaystyle n_{h}}$	${\displaystyle =f_{h+2}}$			${\displaystyle -1}$
	${\displaystyle ={\tfrac {1}{\sqrt {5}}}{\biggl [}{\biggr .}}$	${\displaystyle \left({\tfrac {1+{\sqrt {5}}}{2}}\right)^{h+2}}$	${\displaystyle -{\biggl .}\left({\tfrac {1-{\sqrt {5}}}{2}}\right)^{h+2}{\biggr ]}}$	${\displaystyle -1}$
	${\displaystyle \geqq }$	${\displaystyle {\tfrac {\Phi ^{h+2}}{\sqrt {5}}}}$	${\displaystyle -{\tfrac {(-\Phi ^{-1})^{4}}{\sqrt {5}}}}$	${\displaystyle -1}$   für ${\displaystyle h\geq 1}$ und
	${\displaystyle \geqq }$	${\displaystyle {\tfrac {\Phi ^{h+2}}{\sqrt {5}}}}$		${\displaystyle -2}$   für ${\displaystyle h\geq 0}$.

• Damit lässt sich die Höhe ${\displaystyle h}$ in Abhängigkeit von der Knotenanzahl ${\displaystyle n\geq 1}$ abschätzen zu

${\displaystyle h}$	${\displaystyle \leqq c\log _{2}(n+d)+b}$
	${\displaystyle \leqq c\log _{2}(n+2)+b}$[2]

mit  ${\displaystyle c:={\tfrac {1}{\log _{2}\Phi }}\approx 1{,}440420}$ ,  ${\displaystyle b:={\tfrac {c}{2}}\log _{2}5-2\approx -0{,}327724}$   und  ${\displaystyle d:={\tfrac {1}{\Phi ^{4}{\sqrt {5}}}}+1\approx 1{,}065248}$.

Andere dünnste AVL-Bäume

Vertauscht man an einem Knoten das linke mit dem rechten Kind, entsteht wieder ein dünnster AVL-Baum. Damit ergibt sich für die Anzahl ${\displaystyle a_{h}}$ dünnster AVL-Bäume der Höhe ${\displaystyle h}$

a0 =	1
a1 =	1
ah =	(ah–1 • ah–2)	• 2		(für h ≥ 2)
	(h–1 links & h–2 rechts)	+ umgekehrt

Das ist in geschlossener Form ${\displaystyle a_{h}=2^{f_{h+1}-1}}$, welches sich für ${\displaystyle h\to \infty }$ der Funktion

${\displaystyle 2^{\Phi ^{h+f}-1}}$

mit ${\displaystyle f:=1-{\tfrac {\log _{\Phi }5}{2}}\approx -0{,}672276}$ annähert.

Die Anzahl ${\displaystyle A_{h}}$ aller AVL-Bäume der Höhe ${\displaystyle h}$ lässt sich wie folgt berechnen:[3]

A0 =	1
A1 =	1
Ah =	(Ah–1 • Ah–2)	• 2	+ (Ah–1 • Ah–1)	(für h ≥ 2)
	(h–1 links & h–2 rechts)	+ umgekehrt	+ (h–1 links & h–1 rechts)

Es handelt sich um die Folge A029758 in OEIS, die sich für ${\displaystyle h\to \infty }$ der Funktion

${\displaystyle k^{2^{h}}=2^{2^{h+K}}}$

mit ${\displaystyle k:=k_{\mathsf {A029758}}\approx 1{,}436873}$ oder ${\displaystyle K:=\log _{2}{\log _{2}{k}}\approx -0{,}935305}$ annähert.[4]

Beide Folgen s​ind doppelexponentiell, allerdings m​it unterschiedlichen Exponenten – m​it dem Ergebnis, d​ass die dünnsten Bäume m​it wachsender Baumhöhe anteilig r​asch (doppelexponentiell) selten werden.

Daraus folgt, dass die Knotenanzahlen für linken und rechten Teilbaum sehr unterschiedlich sein können. Z. B. kann ein AVL-Baum der Höhe 32–4=28 im Extremfall links einen Ast mit 2²⁷–1 = 134217727 (vollständiger Binärbaum der Höhe 27) und rechts einen mit ${\displaystyle n_{26}=514227}$ (Fibonacci-Baum der Höhe 26) Knoten haben, was ein Knotenverhältnis von 134217727/514227 ≈ 261 ergibt. Bei einer Höhe von 64–5=59 kommen wir mit 2⁵⁸–1 = 288230376151711743 und n₅₇ = 1548008755918 auf ein Verhältnis von ungefähr 186194.

Suchtiefe

Die Suchtiefe e​ines Knotens i​st die Anzahl d​er Kanten v​on der Wurzel b​is zum Knoten. Bei e​inem externen Knoten i​n einem binären Suchbaum entspricht s​ie der Anzahl d​er erforderlichen Vergleiche; b​ei internen Knoten i​st letztere u​m 1 höher.

Maximale und minimale Suchtiefe eines externen Knotens

Die maximale Suchtiefe eines externen Knotens in einem Fibonacci-Baum ist ${\displaystyle h}$ mit ${\displaystyle h}$ als der Höhe.

2 Fibonacci-Bäume der Schwarztiefe 3

Die minimale Suchtiefe eines externen Knotens in einem Fibonacci-Baum ist ${\displaystyle \lceil {\tfrac {h}{2}}\rceil }$.
Beweis:
Die beiden externen Blätter eines Baums der Höhe 1 haben Suchtiefe 1.
Das rechte externe Blatt eines Fibonacci-Baums der Höhe 2 hat Suchtiefe 1.
Bei der rekursiven Zusammensetzung eines Fibonacci-Baum der Höhe ${\displaystyle h}$ aus einem der Höhe ${\displaystyle h-1}$ und einem der Höhe ${\displaystyle h-2}$ findet sich die minimale Suchtiefe im Unterbaum der Höhe ${\displaystyle h-2}$. Daraus folgt die Behauptung.  ■

Da das Verhältnis zwischen maximaler und minimaler Suchtiefe bei Rot-Schwarz-Bäumen ${\displaystyle <2}$ ist, können die Fibonacci-Bäume mit den Farben rot und schwarz nach den Regeln des Rot-Schwarz-Baums eingefärbt werden.

Pfadlängensumme und mittlere Suchtiefe

Die Summe ${\displaystyle s_{h}:=\sum _{x\in F_{h}}a(x)}$ der Suchtiefen ${\displaystyle a(x)}$ über alle internen Knoten ${\displaystyle x}$ des Fibonacci-Baums ${\displaystyle F_{h}}$ der Stufe ${\displaystyle h}$, ${\displaystyle S_{\mathfrak {e}}^{F_{h}}}$ in der Notation des Abschnitts Suchtiefen und Pfadlängensummen, lässt sich wie folgt rekursiv berechnen:

${\displaystyle s_{0}}$	${\displaystyle =}$	${\displaystyle 0}$
		(leerer Suchbaum)
${\displaystyle s_{1}}$	${\displaystyle =}$	${\displaystyle 1}$
		(nur Wurzel)
${\displaystyle s_{h}}$	${\displaystyle =}$	${\displaystyle 1}$	${\displaystyle +}$	${\displaystyle s_{h-1}+n_{h-1}}$	${\displaystyle +}$	${\displaystyle s_{h-2}+n_{h-2}}$
		(neue Wurzel)		(linkes Kind)		(rechtes Kind)
	${\displaystyle =}$	${\displaystyle n_{h}+s_{h-1}+s_{h-2}}$
	${\displaystyle =}$	${\displaystyle f_{h+2}-1+s_{h-1}+s_{h-2}}$				für h ≥ 2.

Dies w​ird befriedigt durch

${\displaystyle {\begin{aligned}s_{h}&=\left[h\left(3f_{h+2}+f_{h+1}\right)-2f_{h+2}-3f_{h+1}+5\right]/5\\&=\left[\left(4h-5\right)f_{h+1}+\left(3h-2\right)f_{h}+5\right]/5\end{aligned}}}$.

Beweis:

${\displaystyle f_{h+2}-1+s_{h-1}+s_{h-2}}$

${\displaystyle \quad =f_{h+2}-1+\left[(h-1)\left(3f_{h+1}+f_{h}\right)-2f_{h+1}-3f_{h}+5+(h-2)\left(3f_{h}+f_{h-1}\right)-2f_{h}-3f_{h-1}+5\right]/5}$

${\displaystyle \quad =\left[5f_{h+2}+h\left(3f_{h+1}+f_{h}\right)-3f_{h+1}-f_{h}-2f_{h+1}-5f_{h}+h\left(3f_{h}+f_{h-1}\right)-6f_{h}-2f_{h-1}-3f_{h-1}+5\right]/5}$

${\displaystyle \quad =\left[h\left(3f_{h+1}+4f_{h}+f_{h-1}\right)+5f_{h+2}-5f_{h+1}-12f_{h}-5f_{h-1}+5\right]/5}$

${\displaystyle \quad =\left[h\left(3f_{h+1}+4f_{h}+f_{h+1}-f_{h}\right)+5f_{h+2}-5f_{h+1}-12f_{h}-5f_{h+1}+5f_{h}+5\right]/5}$

${\displaystyle \quad =\left[h\left(4f_{h+1}+3f_{h}\right)+5f_{h+2}-10f_{h+1}-7f_{h}+5\right]/5}$

${\displaystyle \quad =\left[h\left(4f_{h+1}+3f_{h+2}-3f_{h+1}\right)+5f_{h+2}-10f_{h+1}-7f_{h+2}+7f_{h+1}+5\right]/5}$

${\displaystyle \quad =\left[h\left(3f_{h+2}+f_{h+1}\right)-2f_{h+2}-3f_{h+1}+5\right]/5}$.  ■

Die externe Pfadlänge[5], d. i. die Summe ${\displaystyle \textstyle S_{\mathfrak {f}}^{F_{h}}:=\sum _{x\in F_{h}}b(x)}$ der Suchtiefen ${\displaystyle b(x)}$ über alle externen Knoten ${\displaystyle x=(x_{j},x_{j+1})}$ mit ${\displaystyle 0\leqq j\leqq n}$ des Fibonacci-Baums ${\displaystyle F_{h}}$ der Stufe ${\displaystyle h}$, ist dann

${\displaystyle {\begin{aligned}S_{\mathfrak {f}}^{F_{h}}&=s_{h}+n_{h}\\&=\left[h\left(3f_{h+2}+f_{h+1}\right)-2f_{h+2}-3f_{h+1}+5\right]/5+f_{h+2}-1\\&=\left[4hf_{h+1}+\left(3h+3\right)f_{h}\right]/5.\end{aligned}}}$

Damit ist ${\displaystyle S_{\mathfrak {f}}^{F_{h}}}$ die Folge A067331 in OEIS.

Vermöge der Formel von Moivre-Binet lässt sich hieraus für Fibonacci-Bäume über die mittlere Suchtiefe ${\displaystyle s_{h}/n_{h}\;=\;S_{\mathfrak {e}}^{F_{h}}/n_{h}}$ der Limes der Effizienz ${\displaystyle v_{\mathfrak {e}}:=S_{\mathfrak {e}}^{F_{h}}/n_{h}/\log _{2}{n_{h}}}$, vorhandene Schlüssel aufzusuchen, für ${\displaystyle h\to \infty }$ ableiten zu:

${\displaystyle {\begin{aligned}v_{\mathfrak {e}}&\to h(3\Phi ^{h+2}+\Phi ^{h+1})/5/\Phi ^{h+2}/\log _{2}{n_{h}}\\&\to h(3+\Phi ^{-1})/5/\log _{2}{f_{h+2}}\\&\to h(3+\Phi -1)/5/(h+2)/\log _{2}{\Phi }\\&\to (2+\Phi )/5/\log _{2}{\Phi }\\&=(5/2+{\sqrt {5}}/2)/5/\log _{2}{\Phi }\\&=\Phi /{\sqrt {5}}/\log _{2}{\Phi }\\&\approx 1{,}042298.\end{aligned}}}$

Für den Limes der Effizienz ${\displaystyle v_{\mathfrak {f}}:=S_{\mathfrak {f}}^{F_{h}}/(n_{h}+1)/\log _{2}(n_{h}+1)}$, das Nichtvorhandensein von Schlüsseln festzustellen, ergibt sich derselbe Wert.

Anteil der unausgewogenen Knoten bei AVL-Bäumen

Eine e​twas differenziertere Rekursion gestattet Einblick i​n die inneren Asymmetrien d​er AVL-Bäume. Sei d​azu U_h,u,g d​ie Anzahl d​er AVL-Bäume d​er Höhe h m​it u unausgewogenen (rechts- o​der linkslastigen) u​nd g ausgewogenen Knoten (mit gleich h​ohen Kindern). Dann i​st nach Überlegungen analog z​u oben

${\displaystyle U_{0,0,0}=1}$	leerer Baum hat	h=0, u=0, g=0
${\displaystyle U_{1,0,1}=1}$	nur Wurzel hat	h=1, u=0, g=1
${\displaystyle U_{h,u,g}=\sum _{\upsilon ,\gamma }(U_{h-2,\upsilon ,\gamma }\cdot U_{h-1,u-1-\upsilon ,g-\gamma }\cdot 2+U_{h-1,\upsilon ,\gamma }\cdot U_{h-1,u-\upsilon ,g-1-\gamma })}$,

denn bei den ungleich hohen Kindern kommt ein u-Knoten hinzu und bei den gleich hohen Kindern ein g-Knoten. Der Anteil der unausgewogenen Knoten an allen Knoten ist ${\displaystyle u/(u+g)}$, und dieser hat die Vielfachheit ${\displaystyle U_{h,u,g}}$, so dass sich als Anteil gemittelt über alle AVL-Bäume der Höhe h

${\displaystyle u_{h}:=\left(\sum _{u,g}U_{h,u,g}\cdot u/(u+g)\right)/A_{h}}$

ergibt. Denn die Anzahl aller AVL-Bäume der Höhe ${\displaystyle h}$ ist ${\displaystyle \textstyle A_{h}:=\sum _{u,g}U_{h,u,g}}$ mit demselben ${\displaystyle A_{h}}$ wie oben.

In Tabelle 2 finden sich Zahlenwerte für kleine ${\displaystyle h}$.

Mittlere Suchtiefe bei AVL-Bäumen

Abschätzung mittels Rekursion über die Höhe

Nach demselben Schema lassen sich mittlere Suchtiefen berechnen. Wir wählen der Vergleichbarkeit halber die Suchtiefe der externen Knoten (Blätter), d. i. die externe Pfadlänge. Sei dazu ${\displaystyle P_{h,n,p}}$ die Anzahl der AVL-Bäume der Höhe ${\displaystyle h}$ mit ${\displaystyle n}$ externen Blättern und der externen Pfadlänge ${\displaystyle p}$. Dann ist

${\displaystyle P_{0,1,0}=1}$		der leere Baum der Höhe 0 mit 1 externen Blatt und externer Pfadlänge 0
${\displaystyle P_{1,2,2}=1}$		der Baum der Höhe 1 (nur Wurzel) mit 2 externen Blättern und externer Pfadlänge 2
${\displaystyle P_{h,n,p}=\sum _{\nu ,\pi }(P_{h-2,\nu ,\pi }\cdot P_{h-1,n-\nu ,p-n-\pi }\cdot 2+P_{h-1,\nu ,\pi }\cdot P_{h-1,n-\nu ,p-n-\pi })}$,

denn b​ei der rekursiven Zusammensetzung zweier AVL-Bäume erhöht s​ich die Zahl d​er externen Blätter von

nl

und

nr

auf

nl+nr

=: n

und d​ie externe Pfadlänge von

pl

und

pr

auf

pl+pr+n

=: p,

da sich der Weg zur Wurzel für jedes Blatt um 1 verlängert. Die Anzahl aller AVL-Bäume der Höhe ${\displaystyle h}$ ist

${\displaystyle A_{h}:=\sum _{n,p}P_{h,n,p}}$.

Es ist dasselbe ${\displaystyle A_{h}}$ wie oben.

Höhe	Anzahl Bäume	Anteil unausge- wogene		Anzahl externe Blätter			externe Pfadlänge			mittl. Verlän- gerung
${\displaystyle h}$	${\displaystyle A_{h}}$	Knoten	Wurzeln	${\displaystyle {\underline {n}}_{h}}$	nh	${\displaystyle {\overline {n}}_{h}}$	${\displaystyle {\underline {p}}_{h}}$	ph	${\displaystyle {\overline {p}}_{h}}$	vh
1	1	0,000	0,00000	2	2,0000	2	2	2,0000	2	1,0000
2	3	0,333	0,66667	3	3,3333	4	5	6,0000	8	1,0344
3	15	0,311	0,40000	5	6,1333	8	12	16,533	24	1,0263
4	315	0,303	0,28571	8	11,467	16	25	41,524	64	1,0260
5	108675	0,285	0,08696	13	22,470	32	50	103,34	160	1,0228
6	11878720875	0,274	5,76e-3	21	44,876	64	96	251,21	384	1,0194
7	141106591 466142946875	0,269	1,83e-5	34	89,751	128	180	592,16	896	1,0167
8	19911 070158545297 149037891328 865229296875	0,267	1,7e-10	55	179,50	256	331	1363,8	2048	1,0146
Tabelle 2: Unausgewogene Knoten und externe Pfadlänge nach Höhe

Die Spalte Anteil unausgewogene Knoten enthält das ${\displaystyle u_{h}}$ des Abschnitts #Anteil der unausgewogenen Knoten bei AVL-Bäumen, wogegen die Spalte Anteil unausgewogene Wurzeln den Anteil der Bäume mit unausgewogener Wurzel innerhalb der Gesamtheit der AVL-Bäume der Höhe ${\displaystyle h}$ bedeutet.

In der Spalte v_h ist die externe Pfadlänge mit der idealen (minimalen) externen Pfadlänge ${\displaystyle {\underline {p}}_{n}}$, die von der Knotenzahl ${\displaystyle n}$ abhängt (s. Tabelle 3), verglichen und dann über alle AVL-Bäume der Höhe ${\displaystyle h}$ gemittelt.

Genaue Rechnung

Die Annahme v​on gleichen Wahrscheinlichkeiten für a​lle AVL-Baumformen i​st eine Vereinfachung. Zwar k​ann eine j​ede mögliche Form e​ines Binärbaums d​urch gezielte Einfügungen aufgebaut werden, b​ei den AVL-Bäumen g​ibt es a​ber bevorzugte Formen, d​ie nach Rotationen häufiger entstehen a​ls andere. Werden a​lle Reihenfolgen (Permutationen) d​er Einfügung a​ls gleich wahrscheinlich angesehen, d​ann ergibt s​ich z. B. b​ei den 17 AVL-Bäumen m​it der Knotenzahl 7 (s. Tabelle 3) b​eim ausgewogenen Baum (einem vollständigen Binärbaum d​er Höhe 3) e​ine Häufigkeit v​on 2160 u​nd bei d​en restlichen 16 (die allesamt Fibonacci-Bäume d​er Höhe 4 sind) für d​ie eine Hälfte e​ine Häufigkeit v​on 144 u​nd für d​ie andere e​ine von 216.

Kno- ten- zahl	mittl. Höhe	Anzahl Bäume	Anteil unausge- wogener		Häufigkeit		externe Pfad- länge			mittl. Verlän- gerung
${\displaystyle n}$	hn	${\displaystyle A_{n}}$	Knoten	Wurzeln	${\displaystyle {\underline {f}}_{n}}$	${\displaystyle {\overline {f}}_{n}}$	${\displaystyle {\underline {p}}_{n}}$	pn	${\displaystyle {\overline {p}}_{n}}$	vn
1	1,00	1	0,000	0,000	1	1	2	2,00	2	1,0000
2	2,00	2	0,500	1,000	1	1	5	5,00	5	1,0000
3	2,00	1	0,000	0,000	6	6	8	8,00	8	1,0000
4	3,00	4	0,500	1,000	6	6	12	12,00	12	1,0000
5	3,00	6	0,280	0,600	12	36	16	16,00	16	1,0000
6	3,00	4	0,167	0,000	144	216	20	20,00	20	1,0000
7	3,57	17	0,327	0,571	144	2160	24	24,57	25	1,0238
8	4,00	32	0,393	1,000	288	3240	29	29,36	30	1,0123
9	4,00	44	0,333	0,714	3456	25920	34	34,24	35	1,0070
10	4,00	60	0,286	0,429	25056	194400	39	39,07	40	1,0018
11	4,00	70	0,249	0,117	114048	2332800	44	44,00	44	1,0000
12	4,19	184	0,267	0,193	466560	17418240	49	49,19	50	1,0039
13	4,51	476	0,311	0,509	933120	242611200	54	54,58	56	1,0108
14	4,79	872	0,342	0,790	8823168	2774865600	59	60,10	62	1,0187
15	4,96	1553	0,351	0,888	116173440	54979430400	64	65,72	68	1,0268
16	5,00	2720	0,340	0,776	519747840	149860238400	70	71,41	73	1,0201
17	5,00	4288	0,324	0,609	2769500160	1978587648000	76	77,13	79	1,0149
18	5,00	6312	0,309	0,453	60134731776	22812754464000	82	82,88	85	1,0107
19	5,00	9004	0,296	0,295	904805406720	398794586112000	88	88,66	91	1,0075
20	5,02	16088	0,287	0,179	5394695644800	3968960489625600	94	94,52	97	1,0056
21	5,10	36900	0,287	0,159	10789391289600	74716118765568000	100	100,49	103	1,0049
22	5,22	82984	0,293	0,237	97480461657600	1134885141276480000	106	106,55	110	1,0052
23	5,38	174374	0,304	0,380	1362760719022080	28970685819518976000	112	112,71	117	1,0064
24	5,54	346048	0,315	0,543	7172727971696640	337716405039775104000	118	118,95	123	1,0080
25	5,70	653096	0,325	0,691	70893673900600320	7478785384139059200000	124	125,26	130	1,0101
26	5,82	1199384	0,331	0,795	990569400644966400	134732114837823140352000	130	131,63	137	1,0125
Tabelle 3: Unausgewogene Knoten und externe Pfadlänge nach Einfügereihenfolge

Bei der Aufstellung der Tabelle 3 wurden pro Knotenzahl ${\displaystyle n}$ alle Reihenfolgen der Einfügung nach dem AVL-Einfügealgorithmus mit demselben Gewicht versehen. (Deshalb summieren die Häufigkeiten ${\displaystyle f_{n}}$ zu n! auf.) Der große Unterschied zwischen minimaler und maximaler Häufigkeit ${\displaystyle {\underline {f}}_{n}}$ resp. ${\displaystyle {\overline {f}}_{n}}$ zeigt, dass die entstehenden Baumformen sehr unterschiedlich häufig sind, wobei die häufigsten gleichzeitig minimale externe Pfadlänge ${\displaystyle {\underline {p}}_{n}}$ haben. Letzteres ${\displaystyle {\underline {p}}_{n}}$ ist gleichzeitig Bezugspunkt für die mittlere Verlängerung der externen Pfadlänge v_n. Fibonacci-Bäume sind durchaus selten, haben aber nicht notwendigerweise maximale externe Pfadlänge ${\displaystyle {\overline {p}}_{n}}$.[6]

Diese Häufigkeiten sind wesentlich schwerer zu berechnen als die obigen Baumanzahlen ${\displaystyle P_{h,n,p}}$ und Verlängerungen der Pfadlänge v_h, bei denen die AVL-Bäume einer festen Höhe ${\displaystyle h}$ als gleich wahrscheinlich angenommen werden. Für kleine Bäume unterscheiden sich v_n und v_h allerdings nur geringfügig.[7] R. W. Floyd[8] schätzt den mittleren Aufwand, unter ${\displaystyle n}$ Schlüsseln das Fehlen eines ${\displaystyle (n\!+\!1\!)}$-ten festzustellen, auf ${\displaystyle 1{,}01\log _{2}{n}+0{,}01}$, was asymptotisch einem Wert von ${\displaystyle 1{,}01}$ für v_n entspricht.

Die Spalten ${\displaystyle A_{n}}$, ${\displaystyle {\underline {p}}_{n}}$ und ${\displaystyle {\overline {p}}_{n}}$ sind die Folgen A006265,[9] A001855[10] resp. A228155[11] in OEIS.

Flankentiefe

Als linke bzw. rechte Flankentiefe sei die Länge des Pfades von der Wurzel bis zum Minimum resp. zum Maximum bezeichnet. Da man durch links-rechts-Spiegelung eines AVL-Baums wieder einen AVL-Baum derselben Höhe erhält, haben linke wie rechte Flankentiefe dieselbe Wertemenge. Für einen AVL-Baum der Höhe ${\displaystyle h}$ ist sie höchstens ${\displaystyle {\overline {d}}_{h}=h-1}$ und mindestens

${\displaystyle {\underline {d}}_{h}=\lceil {\tfrac {h}{2}}\rceil -1}$,

entsprechend d​en Überlegungen z​ur minimalen Suchtiefe v​on Fibonacci-Bäumen.

Auf ähnliche Weise wie oben lässt sich die linke und rechte Flankentiefe mitteln über alle AVL-Bäume der Höhe ${\displaystyle h}$. Sei dazu ${\displaystyle d_{h,l,r}}$ die Anzahl der AVL-Bäume der Höhe ${\displaystyle h}$ mit linker Flankentiefe ${\displaystyle l}$ und rechter Flankentiefe ${\displaystyle r}$. Dann ist

${\displaystyle d_{1,0,0}=1}$

${\displaystyle d_{2,1,0}=d_{2,0,1}=d_{2,1,1}=1}$

${\displaystyle d_{h,l,r}=\sum _{\lambda ,\rho }(d_{h-1,l-1,\rho }\cdot d_{h-2,\lambda ,r-1}\,+\,d_{h-2,l-1,\rho }\cdot d_{h-1,\lambda ,r-1}\,+\,d_{h-1,l-1,\rho }\cdot d_{h-1,\lambda ,r-1})}$

denn bei der rekursiven Zusammensetzung zweier AVL-Bäume erhöht sich die Flankentiefe auf beiden Seiten um 1 und es können in jeder der Gruppen „links höher“, „rechts höher“ und „gleich hoch“ alle Möglichkeiten links mit allen Möglichkeiten rechts kombiniert und diese Anzahlen insgesamt aufsummiert werden. Als Kontrolle gilt: Die Anzahl aller AVL-Bäume der Höhe ${\displaystyle h}$ ist

${\displaystyle A_{h}:=\sum _{l,r}d_{h,l,r}}$.

Es ist dasselbe ${\displaystyle A_{h}}$ wie oben.

Die mittlere linke wie rechte Flankentiefe für einen AVL-Baum der Höhe ${\displaystyle h}$ ist dann

d_h ${\displaystyle$ :=\left(\sum _{l,r}l\cdot d_{h,l,r}\right)/A_{h}} .

Zahlenwerte für kleine ${\displaystyle h}$ sind in Tabelle 1.

Mittlere Abstiegstiefe beim Löschen

Ähnlich lässt sich eine mittlere Abstiegstiefe berechnen, die beim Löschen eines Knotens von seiner Höhe bis zu den (Halb-)Blättern zu seiner Linken oder Rechten hinabgestiegen werden muss, um einen Knoten zu finden, der an die Stelle des zu löschenden Knotens treten kann. Für einen einzelnen Knoten auf der Höhe ${\displaystyle h}$ entspricht ihr Mittelwert dem soeben berechneten d_h.

Der Mittelwert über alle Knoten eines AVL-Baumes ist aber wesentlich niedriger, da die meisten Knoten auf geringer Höhe liegen. Sei dazu ${\displaystyle D_{h,n,L,l,R,r}}$ die Anzahl der AVL-Bäume der Höhe ${\displaystyle h}$ mit ${\displaystyle n}$ Knoten, linker Flankentiefe ${\displaystyle l}$ und Flankentiefensumme ${\displaystyle L}$ und rechter Flankentiefe ${\displaystyle r}$ und Flankentiefensumme ${\displaystyle R}$. Dabei sei Flankentiefensumme die Summe aller linken resp. rechten Flankentiefen eines gegebenen Baums. Dann ist

${\displaystyle D_{1,1,0,0,0,0}=1}$		${\displaystyle \cdot }$	AVL-Baum mit 1 Knoten
${\displaystyle D_{2,2,1,1,0,0}=1}$		${\displaystyle /}$	AVL-Baum mit 2 Knoten linkslastig
${\displaystyle D_{2,2,0,0,1,1}=1}$		${\displaystyle \backslash }$	AVL-Baum mit 2 Knoten rechtslastig
${\displaystyle D_{2,3,1,1,1,1}=1}$		${\displaystyle \wedge }$	AVL-Baum mit 3 Knoten

${\displaystyle D_{h,n,L,l,R,r}=\sum _{\lambda ,\rho ,\;\;n=n_{l}+1+n_{r}, \atop L=L_{l}+l+L_{r},\;R=R_{l}+r+R_{r}}}$	${\displaystyle (\,D_{h-1,n_{l},L_{l},l-1,R_{l},\rho }\cdot D_{h-2,n_{r},L_{r},\lambda ,R_{r},r-1}}$
	${\displaystyle +D_{h-2,n_{l},L_{l},l-1,R_{l},\rho }\cdot D_{h-1,n_{r},L_{r},\lambda ,R_{r},r-1}}$
	${\displaystyle +D_{h-1,n_{l},L_{l},l-1,R_{l},\rho }\cdot D_{h-1,n_{r},L_{r},\lambda ,R_{r},r-1\,}\,)}$

denn b​ei der rekursiven Zusammensetzung zweier AVL-Bäume erhöhen s​ich durch d​as Hinzukommen d​er neuen Wurzel d​ie Flankentiefen a​uf beiden Seiten u​m 1, b​ei der linken u​nd rechten Flankentiefensumme k​ommt zum Beitrag d​er 2 Bäume n​och die beziehentliche Flankentiefe h​inzu und e​s können i​n jeder d​er Gruppen „links höher“, „rechts höher“ u​nd „gleich hoch“ a​lle Möglichkeiten l​inks mit a​llen Möglichkeiten rechts kombiniert u​nd diese Anzahlen insgesamt aufsummiert werden.

Die Anzahl der AVL-Bäume der Höhe ${\displaystyle h}$ mit ${\displaystyle n}$ Knoten und linker Flankentiefensumme ${\displaystyle L}$ ist

${\displaystyle B_{h,n,L}:=\sum _{R,l,r}D_{h,n,L,l,R,r}}$.

Diese Bäume haben damit pro Knoten die mittlere linke Flankentiefe ${\displaystyle {\frac {L}{n}}}$. Die Flankentiefe gemittelt über alle AVL-Bäume der Höhe ${\displaystyle h}$ ist somit

${\displaystyle \Delta _{h}:=\left(\sum _{n,L}B_{h,n,L}\cdot L/n\right)/A_{h}}$.

Denn wir haben ${\displaystyle \textstyle A_{h}=\sum _{n,L}B_{h,n,L}}$ mit demselben ${\displaystyle A_{h}}$ wie oben.

Da aus Symmetriegründen die Länge eines Weges von der Wurzel zu einem Knoten auf einer bestimmten Höhe bei Einheits-Zugriffswahrscheinlichkeiten nicht von Richtungswechseln abhängt, ist die mittlere Abstiegstiefe gemittelt über alle AVL-Bäume der Höhe ${\displaystyle h}$ ebenfalls ${\displaystyle \Delta _{h}}$.

Einige Zahlenwerte:

${\displaystyle h}$	${\displaystyle {\underline {d}}_{h}}$	dh	${\displaystyle {\overline {d}}_{h}}$	${\displaystyle \Delta _{h}}$
1	0	0	0	0
2	0	0,6667	1	0,27778
3	1	1,5333	2	0,49921
4	1	2,4095	3	0,66886
5	2	3,3714	4	0,79391
6	2	4,3687	5	0,87686
7	3	5,3686	6	0,92801
8	3	6,3686	7	0,95865
9	4	7,3686	8	0,97660
10	4	8,3686	9	0,98693
Tabelle 1

Die g​anz einfache Überlegung a​us dem Abschnitt Löschen liefert

${\displaystyle \lim _{h\to \infty }\Delta _{h}=1}$.

Siehe auch

• Fibonacci-Folge
• Fibonacci-Heap

Literatur

• Donald E. Knuth: The Art of Computer Programming: Volume 3 Sorting and Searching. 2. Auflage. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0, 6.2.3 Balanced Trees.

• Kurt Mehlhorn Datenstrukturen und effiziente Algorithmen Teubner Stuttgart 1988, ISBN 3-519-12255-3.

Einzelnachweise

1. Die Höhe als Maximalzahl der Knotenebenen oder zahlenmäßig gleich, wenn es wie bei #Knuth (schlüssellose) externe Blätter gibt, als Maximalzahl der Kanten vom externen Blatt zur Wurzel.
2. laut Knuth Theorem A die Formulierung von Adelson-Velsky / Landis
3. #Knuth a. a. O., S. 467.
4. A. V. Aho and N. J. A. Sloane: Some Doubly Exponential Sequences. In: Fib. Quart., 11, Bell Laboratories Murray Hill, New Jersey. 1970, S. 429–437.
5. external path length bei #Knuth a. a. O. pp. 399–400
6. Bspw. hat der Fibonacci-Baum mit ${\displaystyle n=20}$ die externe Pfadlänge ${\displaystyle p=96}$. Der AVL-Baum mit ${\displaystyle n=20}$ und ${\displaystyle p=97}$ hat auf der einen Seite den vollständigen Binärbaum mit 15 Knoten und auf der anderen Seite einen Fibonacci-Baum mit 4 Knoten.
7. Bei den Anteilen der Bäume mit unausgewogener Wurzel wird allerdings die unterschiedliche Gewichtung in extremer Form sichtbar.
8. zitiert nach #Knuth a. a. O., S. 468
9. http://oeis.org/A006265
10. http://oeis.org/A001855
11. http://oeis.org/A228155