Heap (Datenstruktur)
Ein Heap (englisch wörtlich: Haufen oder Halde) in der Informatik ist eine zumeist auf Bäumen basierende abstrakte Datenstruktur. In einem Heap können Objekte oder Elemente abgelegt und aus diesem wieder entnommen werden. Sie dienen damit der Speicherung von Mengen. Den Elementen ist dabei ein Schlüssel zugeordnet, der die Priorität der Elemente festlegt. Häufig werden auch die Elemente selbst als Schlüssel verwendet.
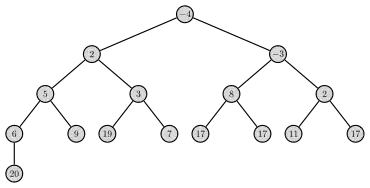
Über die Menge der Schlüssel muss daher eine totale Ordnung festgelegt sein, über welche die Reihenfolge der eingefügten Elemente festgelegt wird. Beispielsweise könnte die Menge der ganzen Zahlen zusammen mit dem Vergleichsoperator < als Schlüsselmenge fungieren.
Der Begriff Heap wird häufig als bedeutungsgleich zu einem partiell geordneten Baum verstanden (siehe Abbildung). Gelegentlich versteht man einschränkend nur eine besondere Implementierungsform eines partiell geordneten Baums, nämlich die Einbettung in ein Feld (Array), als Heap.
Verwendung finden Heaps vor allem dort, wo es darauf ankommt, schnell ein Element mit höchster Priorität aus dem Heap zu entnehmen (HIFO-Prinzip), beispielsweise bei Vorrangwarteschlangen.
Operationen
Je nach Art unterstützen Heaps eine ganze Reihe von Operationen. Die wichtigsten Operationen sind:
Heapify
Heapify ist eine Operation, um die Elemente des Heaps neu anzuordnen, um die Heap-Bedingung aufrechtzuerhalten. Sie erfolgt, wenn ein bestimmter Knoten ein Ungleichgewicht im Heap verursacht. Die Heapify kann in zwei Methoden erfolgen:
Up-Heapify folgt dem Bottom-Up-Ansatz. In diesem Fall wird geprüft, ob die Knoten die Heap-Bedingung erfüllen, indem man in Richtung der Wurzel geht, und wenn Knoten nicht die Heap-Bedingung erfüllen, werden bestimmte Operationen ausgeführt, damit der Baum der Heap-Bedingung folgt.
Down-Heapify folgt dem Top-Down-Ansatz. In diesem Fall wird geprüft, ob die Knoten die Heap-Bedingung erfüllen, indem man in Richtung der Blätter geht, und bestimmte Operationen ausführt, um die Heap-Bedingung herzustellen.
Insert
Das Einfügen eines Elements in den Heap erfolgt, indem das neue Element an das Ende des Heaps gesetzt wird. Weil das neu eingesetzte Element die Eigenschaften des Heaps verzerren kann, wird die Operation Up-Heapify durchgeführt, um die Eigenschaften des Heaps in einem Bottom-up-Ansatz zu erhalten.
Remove
Das Entfernen eines Elements erfolgt, indem das gelöschte Element durch das letzte Element im Heap ersetzt wird. Dann wird das letzte Element aus dem Heap gelöscht. Nun wird das letzte Element an einer Stelle im Heap platziert. Es kann die Heap-Bedingung nicht erfüllen, sodass die Operation Down-Heapify durchgeführt wird, um die Eigenschaften des Heaps aufrechtzuerhalten.
Find-max oder Find-min
Das maximale Element im Max-Heap und das minimale Element im Min-Heap ist die Wurzel des Heaps.
Extract Min oder Extract Max
Dieser Operation gibt das maximale Element im Max-Heap oder das minimale Element im Min-Heap zurück. Dieses Element ist die Wurzel des Heaps.
Daneben werden häufig auch die Operationen changeKey zum Anpassen des Schlüssels und merge zum Verschmelzen zweier Heaps bereitgestellt. Die Operation changeKey wird häufig durch die Nacheinanderausführung der Operationen remove und insert gebildet, wobei nach dem Entfernen und vor dem erneuten Einfügen der Schlüssel angepasst wird. In einigen Fällen bieten Heaps statt changeKey lediglich die Operation decreaseKey an, bei der der Schlüssel lediglich verkleinert werden darf.
Heap-Bedingung
Man unterscheidet Heaps in Min-Heaps und Max-Heaps. Bei Min-Heaps bezeichnet man die Eigenschaft, dass die Schlüssel der Kinder eines Knotens stets größer als oder gleich dem Schlüssel ihres Vaters sind, als Heap-Bedingung. Dies bewirkt, dass an der Wurzel des Baumes stets ein Element mit minimalem Schlüssel im Baum zu finden ist. Umgekehrt verlangt die Heap-Bedingung bei Max-Heaps, dass die Schlüssel der Kinder eines Knotens stets kleiner als oder gleich die ihres Vaters sind. Hier befindet sich an der Wurzel des Baumes immer ein Element mit maximalem Schlüssel.
Mathematisch besteht der Unterschied zwischen beiden Varianten nur in ihrer gegensätzlichen Ordnung der Elemente. Da die Definition von auf- und absteigend rein willkürlich ist, ist es also eine Auslegungsfrage, ob es sich bei einer konkreten Implementierung um einen Min-Heap oder um einen Max-Heap handelt.
Oft kommt es auch vor, dass ein Heap die Heap-Eigenschaft in beiden Richtungen abbilden soll. In diesem Fall werden einfach zwei Heaps geschaffen, wobei der eine nach der Kleiner- und der andere nach der Größer-Relation anordnet. Eine derartige Datenstruktur wird dann Doppelheap oder kurz Deap genannt.
Bei der Verwendung von Doppel-Heaps ist zu beachten, dass nicht jede Implementierung von Heaps dabei ihr Laufzeitverhalten für die einzelnen Operationen behält. Zum Beispiel unterstützen Fibonacci-Heaps nur ein decreaseKey zum Verringern der Schlüssel mit amortisiert konstanter Laufzeit. Ein allgemeineres changeKey zum Ändern des Schlüssels, welches man im Falle eines derartigen Doppel-Heaps benötigen würde, braucht aber amortisiert mindestens logarithmische Laufzeit.
Eine Variante von Heaps, die die Heap-Bedingung nur eingeschränkt bzw. in abgewandelter Form unterstützt, sind sogenannte Min-Max-Heaps. Dabei handelt es sich um Doppel-Heaps, die durch die abgewandelte Form der Heap-Bedingung die Daten in nur einem Baum halten können.
Implementierung
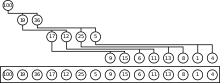
Heaps werden normalerweise mit einer impliziten Heap-Datenstruktur implementiert, bei der es sich um eine implizite Datenstruktur handelt, die aus einem Feld (Array) fester Größe oder einem dynamischen Array besteht, wobei jedes Element den Knoten eines Baums darstellt, dessen Vater-Kind-Relation implizit durch seinen Index definiert wird. Nachdem ein Element in einen Heap eingefügt oder aus einem Heap gelöscht wurde, kann die Heap-Eigenschaft verletzt werden und der Heap muss durch Austauschen von Elementen innerhalb des Arrays ausgeglichen werden.
In einer impliziten Heap-Datenstruktur enthält das erste oder letzte Element die Wurzel. Die nächsten beiden Elemente des Arrays enthalten seine untergeordneten Elemente. Die nächsten vier Elemente enthalten die vier Kinder der beiden Kindknoten usw. Somit würden sich die Kinder des Knotens an Position n an den Positionen 2n und 2n + 1 in einem Array mit Startindex 1 oder an den Positionen 2n + 1 und 2n + 2 in einem Array mit Startindex 0 befinden. Die Berechnung des Index des übergeordneten Knotens des Elements an Position n ist ebenfalls unkompliziert. Bei einem Array mit Startindex 1 befindet sich das übergeordnete Element an Position n / 2. Bei einem Array mit Startindex 0 das übergeordnete Element an der Position (n - 1) / 2. Dies ermöglicht das Durchlaufen des Baums durch einfache Indexberechnungen. Das Ausbalancieren eines Heaps erfolgt durch Austauschen von Elementen, die nicht in Ordnung sind. Da wir einen Heap aus einem Array erstellen können, ohne zusätzlichen Speicher zu benötigen, kann Heapsort verwendet werden, um ein Array in-place zu sortieren.
Verschiedene Arten von Heaps implementieren die Operationen auf unterschiedliche Weise. Insbesondere erfolgt das Einfügen jedoch häufig durch Hinzufügen des neuen Elements am Ende des Heaps im ersten verfügbaren freien Platz. Dies verstößt im Allgemeinen gegen die Heap-Eigenschaft. Daher werden die Elemente nach oben verschoben, bis die Heap-Eigenschaft wiederhergestellt wurde. In ähnlicher Weise wird das Löschen der Wurzel durchgeführt, indem die Wurzel entfernt und dann das letzte Element in die Wurzel eingefügt und zum Ausgleich gesiebt wird. Das Ersetzen erfolgt also durch Löschen der Wurzel und Einfügen des neuen Elements in die Wurzel und Durchsieben, wobei ein Aufwärtsschritt im Vergleich zum Absenken des letzten Elements gefolgt vom Aufsteigen des neuen Elements vermieden wird.
Programmierung
Das folgende Beispiel in der Programmiersprache C++ zeigt die Implementierung der wichtigsten Operationen für einen binären Min-Heap.[1]
#include <iostream>
using namespace std;
void swap(int*, int*); // Hilfsfunktion, die zwei Elemente vertauscht
// Deklariert die Klasse für den Heap
class MinHeap
{
int* elements; // Pointer auf das Array für die Elemente des Heap
int capacity; // Maximale Größe des Heap
int size; // Größe, die die Anzahl der Elemente des Heap speichert
public:
MinHeap(int);
void MinHeapify(int);
int getParent(int index) { return (index - 1) / 2; }
int getLeftChild(int index) { return 2 * index + 1; }
int getRightChild(int index) { return 2 * index + 2; }
int extractMinimum();
void decreaseKey(int, int);
int getMinimumKey() { return elements[0]; }
void deleteKey(int);
void insertKey(int);
};
MinHeap::MinHeap(int capacity) // Konstruktor
{
size = 0;
capacity = capacity;
elements = new int[capacity];
}
// Fügt einen neuen Schlüssel ein
void MinHeap::insertKey(int key)
{
if (size == capacity) // Wenn Kapazität überschritten, Funktion verlassen
{
return;
}
size++; // Erhöht die Größe des Heap um 1
int index = size - 1;
elements[index] = key; // Fügt den Schlüssel am Ende ein
// Der eingefügte Schlüssel wird so lange nach oben geschoben, wie das übergeordnete Element kleiner ist. Damit wird sichergestellt, dass die Heap-Bedingung erfüllt ist.
while (index != 0 && elements[getParent(index)] > elements[index]) // Wenn das Elternelement größer als der Schlüssel ist, werden die Elemente vertauscht.
{
swap(&elements[index], &elements[getParent(index)]);
index = getParent(index); // Aktualisiert den Index des Schlüssels
}
}
// Verringert den Wert des Schlüssels mit dem gegebenen Index
void MinHeap::decreaseKey(int index, int value)
{
if (value >= elements[index]) // Wenn der neue Wert nicht kleiner als der aktuelle Wert ist, Funktion verlassen
{
return;
}
elements[index] = value;
while (index != 0 && elements[getParent(index)] > elements[index])
{
swap(&elements[index], &elements[getParent(index)]);
index = getParent(index);
}
}
// Entfernt das minimale Element vom Heap
int MinHeap::extractMinimum()
{
if (size <= 0)
{
return INT_MAX;
}
if (size == 1)
{
size--;
return elements[0];
}
// Speichert den minimalen Wert und entfernt ihn vom Heap
int root = elements[0];
elements[0] = elements[size - 1];
size--;
MinHeapify(0);
return root;
}
// Löscht den Schlüssel mit dem gegebenen Index
void MinHeap::deleteKey(int index)
{
decreaseKey(index, INT_MIN); // Setzt den Wert auf minus unendlich
extractMinimum();
}
// Rekursive Methode, die die Heap-Bedingung für den Teilbaum mit dem gegebenen Index herstellt. Es wird vorausgesetzt, dass die Teilbäume die Heap-Bedingung schon erfüllen.
void MinHeap::MinHeapify(int index)
{
int leftChild = getLeftChild(index);
int rightChild = getRightChild(index);
int rightIndex = index;
if (leftChild < size && elements[leftChild] < elements[index])
{
rightIndex = leftChild;
}
if (rightChild < size && elements[rightChild] < elements[rightIndex])
{
rightIndex = rightChild;
}
if (rightIndex != index)
{
swap(&elements[index], &elements[rightIndex]); // Vertauscht das Wurzel-Element mit dem Wurzel-Element des rechten Teilbaums
MinHeapify(rightIndex); // Aufruf der rekursiven Methode für den rechten Teilbaum
}
}
// Vertauscht zwei Elemente des Heap
void swap(int* element1, int* element2)
{
int element = *element1;
*element1 = *element2;
*element2 = element;
}
Varianten von Heaps
Es existieren zahlreiche Arten von Heaps mit unterschiedlich gutem Laufzeitverhalten für die verschiedenen Operationen, die sie zur Verfügung stellen. Beispiele für Heaps sind:
Binärer Heap
Ein binärer Heap kann effizient mit linearem Zeitaufwand in konstruiert werden, wobei die Anzahl der Elemente aus der Eingabe bezeichnet. Folgende Operationen arbeiten auf einem Heap und haben eine Worst-Case-Laufzeit von :
- insert – fügt ein neues Element in den Heap ein
- remove – entfernt ein Element
- extractMin – extrahiert das Element mit dem kleinsten Schlüssel
- decreaseKey – verringert den Schlüsselwert eines Elements
Die Operation getMin liefert das kleinste Element im Heap zurück und benötigt dafür konstanten Rechenaufwand.
Binomial-Heap
Binomial-Heaps unterstützen effizient die Operationen
- insert – zum Einfügen eines Elementes,
- remove – zum Entfernen eines Elementes,
- extractMin – zur Rückgabe und zum Entfernen eines Elementes mit minimalem Schlüssel (=höchster Priorität),
- changeKey – zum Ändern des Schlüssels eines Elementes und
- merge – zum Verschmelzen zweier Heaps.
Alle Operationen lassen sich mit einer Worst-Case-Laufzeit von implementieren, wobei die Zahl der aktuell im Heap befindlichen Elemente ist.
Fibonacci-Heap
Ein Fibonacci-Heap ist ähnlich wie ein Binomial-Heap in einer Vorrangwarteschlange realisiert. Das heißt, dass Elemente mit festgelegter Priorität in beliebiger Reihenfolge effizient im Heap gespeichert werden können und stets ein Element mit höchster Priorität entnommen werden kann. Die Priorität der Elemente wird diesen durch Schlüssel aufgeprägt. Über der Menge der Schlüssel muss daher eine Totalordnung bestehen, wie sie zum Beispiel die Kleiner-Gleich-Relation über den ganzen Zahlen darstellt.
Weitere Varianten sind der Min-Max-Heap, der Linksbaum, der Treap und der Radix-Heap.
Außerdem gibt es mit Soft Heaps eine Variante bei der ein besseres Laufzeitverhalten erreicht wird, indem ein bestimmter Anteil der Schlüssel verdorben werden kann. Diese verdorbenen Schlüssel haben nicht mehr ihren ursprünglichen Wert.
Laufzeitverhalten
Die folgende Tabelle gibt die Laufzeiten von verschiedenen Heaps bezüglich ihrer Operationen an.
| Operation | Binärer Heap | Binomial-Heap | Fibonacci-Heap | Pairing-Heap | Linksbaum | 2-3-Heap |
|---|---|---|---|---|---|---|
| amortisiert | amortisiert | amortisiert | ||||
| extract-min | ||||||
| remove | ||||||
| insert | ( vermutet) | oder | ||||
| decrease-key | ( vermutet) | oder | ||||
| merge | ( vermutet) | oder |
Anwendung
Heaps haben ein breites Spektrum an Anwendungen. Häufig ist vor allem der Einsatz in Vorrangwarteschlangen, wie sie bei Servern oder Betriebssystemen zur Festlegung der Ausführungsreihenfolge von Aufgaben benötigt werden.
Daneben gibt es aber auch Anwendungen, die nicht explizit den Einsatz von Warteschlangen verlangen. Allgemein stellt ein Heap eine ideale Datenstruktur für Greedy-Algorithmen dar, die schrittweise lokale optimierte Entscheidungen treffen. So wird zum Beispiel beim Sortieralgorithmus Heapsort ein Binärer Heap zum Sortieren eingesetzt. Fibonacci-Heaps finden beim Algorithmus von Dijkstra bzw. Prim Anwendung.
Literatur
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7, S. 127.
- Donald E. Knuth: The Art of Computer Programming: Volume 3 Sorting and Searching. 2. Auflage. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0, S. 144–155.
Weblinks
Einzelnachweise
- GeeksforGeeks: Binary Heap