Feld (Datentyp)

Ein Feld (englisch field, array [əˈɹeɪ] (Betonung auf 2. Silbe) für ‚Anordnung‘, ‚Aufstellung‘ usw.) ist in der Informatik eine Datenstruktur-Variante, mit deren Verwendung „viele gleichartig strukturierte Daten […] verarbeitet werden sollen“.[1] Der Zugriff auf bestimmte Inhalte eines Felds erfolgt mit Hilfe von Indizes, die dessen Position bezeichnen.

Begriffe

Synonyme

Im Sprachgebrauch und im Wesentlichen geprägt aus dem Einsatz in verschiedenen Programmiersprachen ihrer Terminologie und Entstehungsgeschichte und durch Übersetzung aus dem Englischen, wird der hier – mit der Bedeutung ‚Array‘ – beschriebene Begriff ‚Feld‘ mit unterschiedlichen Ausdrücken belegt: Array ("Area" englisch Areal, Bereich), Tabelle, Vektor, Reihe, Reihung, Datenfeld, Aufstellung, Bereich, Gate Array, Matrix usw. „Der englische und gängigere Begriff für Feld [in dieser Bedeutung] ist Array“.[2]

Auch die einzelnen Elemente eines Arrays werden mit unterschiedlichen Ausdrücken bezeichnet: Element, Komponente, Unterfeld, Feldelement, indizierte Variable – zum Teil ebenfalls „Feld“ oder „Datenfeld“.

Kontextabhängig betrifft die Bezugnahme auf ‚Feld‘ alternativ die Deklarationsebene des Arrays oder gespeicherte Inhalte.

Abweichende Bedeutung

Der Ausdruck ‚Feld‘ wird auch als elementares, Daten beschreibendes Konstrukt im Allgemeinen verstanden, das im Quelltext eines Computerprogramms zur Definition von Speicherplatz verwendet wird. In diesem Sinn ist ein Feld kein Datentyp, sondern es hat einen Datentyp, und es ist unerheblich, ob es einem Array oder einer übergeordneten Datenstruktur, z. B. Verbund oder Record, angehört oder nicht. ‚Feld‘ in diesem Sinn wird damit im Wesentlichen mit Variable oder Datenfeld gleichgesetzt. Literaturbeispiele:

Ausdrücke wie statisches Feld, Klassenfeld, Feldlänge usw. beziehen sich auf ‚Feld‘ in einem allgemeinen Sinn.
‚Feld‘ wird (z. B. in[3]) als typneutrales Datenkonstrukt verwendet.
Gleiches gilt für Texte wie „… Inhalt des Feldes Auftragskennung“ (im Link zu siko.de) und „…behandelt jedes Array Element wie ein eigenes Feld“ in[4] oder Ausdrücke wie „Felder für den Datenaustausch“, „… überträgt Daten zu einem Feld“, „Inhalt des Datenfelds“, „Feldbeschreibung“, „Feldlänge“ etwa in einer Software-Bedienungsanleitung.
Sogar in Unterlagen, die ‚Feld‘ grundsätzlich im Sinne von ‚Array‘ benutzen, wird der Ausdruck ‚Feld‘ auch nicht-arraybezogen verwendet: „Hier hat das Array 10 Felder“ oder „alle anderen Felder besitzen einen undefinierten Wert“ in[5]

Die beiden sich wesentlich unterscheidenden Bedeutungen von ‚Feld‘ sind und waren immer wieder Anlass zu zum Teil heftigen Diskussionen.[6]

Indizes

Zur Adressierung eines einzelnen Elements in einem Feld wird ein ‚Index‘ verwendet. Bei mehrdimensionalen Feldern gibt es für jede Dimension einen Index.

Der Index wird bei ‚Standard-Feldern‘ in höheren Programmiersprachen als Ganzzahl angegeben. ‚Assoziative Felder‘ erlauben dagegen die Verwendung von beliebigen, nicht notwendigerweise numerischen, aber eindeutigen Schlüsselwerten als Indizes.

Sprachspezifische Unterschiede

Grundsätzlich können Arrays in den meisten Programmiersprachen angelegt und verarbeitet werden. Neben den unterschiedlichen Begriffen, die sich in einzelnen Sprachen entwickelt haben, werden Arrays von den Compilern der Programmiersprachen, zum Teil auch in verschiedenen Sprachversionen, unterschiedlich umgesetzt und unterstützt. Beispiele:

Unterscheidung Standardfeld / assoziatives Array / nur Listen durch den Compiler der Programmiersprache
Anzahl der möglichen Dimensionen (in-sich mehrdimensionale Arrays, Array-in-Array)
Maximale Array-Größe
Adressierung der Elemente (ab 0, ab 1 oder ab einem beliebigen Index, gegebenenfalls auch beginnend mit einem negativen Index)
Im Array mögliche Datenformate und -Längen
Anzahl der Unterfelder: fix, dynamisch/variabel je Dimension
Format der Unterfelder: einheitlich für alle Indexwerte, unterschiedlich
Unterstützung für Operationen auf Datenmengen im Array: nur auf Elemente, beliebige Strukturen, ganze Dimension, ganzes Array
Adressierungsverfahren:
- Der Index ist eine Ganzzahl
- Der Index enthält den relativen Abstand zum Array-Beginn
- Der Index ist ein Suchschlüssel

Zugehörige Rechnungen können manuell programmiert werden oder werden durch den Compiler teilweise oder vollständig automatisch durchgeführt.

In den meisten Assemblersprachen ist die Verarbeitung von Arrays zwar möglich, sie wird aber syntaktisch meist nicht speziell unterstützt und muss vom Programmierer explizit „nachgebaut“ werden: Der Programmierer implementiert Array-Elemente so wie auch andere Variablen, reserviert zusätzlich den Speicherplatz für n weitere Ausprägungen. Zur Verarbeitung ermittelt er die Position relevanter Elemente mit geeigneten Algorithmen, zum Beispiel in einem Indexregister, und adressiert sie mit – nicht speziell auf die Array-Verarbeitung ausgerichteten – geeigneten Anweisungen.

Beim Deklarieren werden Arrays in einer sprachspezifischen Syntax formuliert. Beispiele:

FeldX (100) (Datenname plus Anzahl der Array-Elemente in runder Klammer): PL/I
FeldX [100,...] (Datenname plus je Dimension die Anzahl der Array-Elemente in einer eckigen Klammer): C#[7]
FeldX [100][][] (Datenname plus je Dimension in eckigen Klammern die Anzahl der Array-Elemente): C/C++,[8] Java[9]
FeldX array (100) (Schlüsselwort 'array' plus Anzahl der Elemente in runder Klammer): Modula-2
FeldX occurs 100. (Schlüsselwort 'OCCURS' plus Anzahl der Elemente): Cobol
Dim FeldX (100,...) (Schlüsselwort 'Dim' plus Variablenname plus Anzahl Elemente je Dimension (in einer runden Klammer)): VBA, 'Dimension' bei Fortran90/95

Element-Datentyp

In statisch typisierenden Programmiersprachen sind Feldinhalte meist auf Elemente eines einzelnen Datentyps eingeschränkt. Mitunter ist jedoch ein Spezialfall „weitgehend beliebiger Inhalt“ möglich, bei objektorientierten Programmiersprachen oft über Polymorphie der allgemeinen Basisklasse. In dynamisch typisierenden Programmiersprachen können meist Objekte oder allgemeine Datenstrukturen in fast beliebiger Zusammensetzung und Reihenfolge gespeichert werden. In dynamisch typisierenden Programmiersprachen werden jedoch oft nur assoziative Arrays angeboten.

Feldvarianten

Standard-Feld

Standardfeld vs Assoziatives Feld vs 'Feld' als 'Datenfeld'

Mit Hilfe eines Feldes können die Daten eines üblicherweise einheitlichen Datentyps so im Speicher eines Computers abgelegt werden, dass ein Zugriff auf die Daten über Indizes möglich wird. Das Standard-Feld ist im Gegensatz zum assoziativen Feld auf ganzzahlige Indizes zur Adressierung festgelegt. Ein Index beginnt, bei einem (eindimensionalen) Feld mit N Elementen, standardmäßig je nach Programmiersprache bei 0 (C++: 0,1,2,…,N-1) oder 1 (Fortran: 1,2,3,…,N), kann jedoch oftmals auch frei gewählt werden (42,43,44,…,N+41).

Dynamisches Feld

Ein dynamisches Array oder eine Array-Liste eine Listendatenstruktur mit variabler Größe und wahlfreiem Zugriff, wo Elemente hinzugefügt oder entfernt werden können. Es wird von Standardbibliotheken vieler moderner Programmiersprachen zur Verfügung gestellt.

Ein dynamisches Array ist nicht dasselbe wie ein dynamisch zugewiesenes Array, bei dem es sich um ein Array handelt, dessen Größe bei der Zuweisung des Arrays festgelegt wird, obwohl ein dynamisches Array ein solches Array mit fester Größe möglicherweise als Back-End verwendet.

Ein einfaches dynamisches Array kann durch Zuweisen eines Arrays mit fester Größe erstellt werden, das normalerweise größer ist als die Anzahl der unmittelbar erforderlichen Elemente. Die Elemente des dynamischen Arrays werden am Anfang des zugrunde liegenden Arrays zusammenhängend gespeichert, und die verbleibenden Positionen gegen Ende des zugrunde liegenden Arrays werden reserviert oder nicht verwendet. Elemente können am Ende eines dynamischen Arrays in konstanter Laufzeit unter Verwendung des reservierten Speicherplatzes hinzugefügt werden, bis dieser Speicherplatz vollständig belegt ist.

Wenn der gesamte Speicherplatz belegt ist und ein zusätzliches Element hinzugefügt werden soll, muss das zugrunde liegende Array mit fester Größe vergrößert werden. Normalerweise ist die Größenänderung teuer, da ein neues zugrunde liegendes Array zugewiesen und jedes Element aus dem ursprünglichen Array kopiert werden muss. Elemente können in konstanter Zeit vom Ende eines dynamischen Arrays entfernt werden, da keine Größenänderung erforderlich ist. Die Anzahl der Elemente, die vom Inhalt des dynamischen Arrays verwendet werden, ist seine logische Größe, während die Größe des zugrunde liegenden Arrays als Kapazität oder physische Größe des dynamischen Arrays bezeichnet wird. Dies ist die maximale mögliche Größe, die verwendet werden kann, ohne Daten zu verschieben.

Ein dynamisches Array wird benötigt, wenn die maximale logische Größe nicht festgelegt ist oder nicht berechnet werden kann, bevor der Speicherplatz für das Array reserviert wird.

Assoziatives Feld

Eine Sonderform bildet das „assoziative Array“. Es verwendet keine notwendigerweise ganzzahligen numerischen Indizes, sondern Schlüssel zur Adressierung der Elemente. Diese Schlüssel können prinzipiell beliebigen Typs sein, zum Beispiel Zeichenketten, müssen aber ein Element eindeutig identifizieren. Beispiel: Die Produktnummer ist der Index, mit dem Daten zu einem bestimmten Produkt in einer Produkttabelle indiziert werden, z. B.: Produkt = ProdBezeichn (ProdNr). Am häufigsten werden assoziative Felder als Hashtabelle umgesetzt.

Bei assoziativen Arrays muss – als zusätzlicher Teil der Adressrechnung (siehe unten) – die Position der Daten anhand des als Schlüssel festgelegten Datenfeldes ermittelt werden. „Assoziativ“ werden solche Felder nur genannt, wenn dieser Teil der Adressierung von der Programmiersprache automatisch berechnet wird.

Dimensionen

In den meisten Programmiersprachen kann ein Feld – und damit die darin gespeicherten Daten – nicht nur ein-, sondern mehrdimensional sein. Bei mehrdimensionalen Feldern wird zur Adressierung ihrer Elemente für jede Dimension ein eigener Index verwendet. Zum Begriff der Dimension können die nachfolgenden Varianten unterschieden werden. In den Beispielen wird ein symbolischer Beispielcode verwendet, der Startindex sei 1.

Eindimensionale Felder

Die Feldelemente werden wie in einer Liste als elementares Datenfeld oder als Verbund mit mehreren Elementarfeldern geführt. Der Zugriff auf die Informationen erfolgt über 'ArrayName (index)'.

Beispiele

1. eindimensional (wie eine ‚Liste‘)

Vektor := array(3) of float  // Deklaration einer 1-dimensionalen Liste namens „Vektor“ mit 3 ‚freien Plätzen‘
 Vektor := (0.5, 1.7, -0.2)   // der Punkt (x=0.5 ; y=1.7 ; z=-0.2) im ℝ³

Vektor[2] liefert so die y-Komponente mit dem Wert 1.7.

2. eindimensional (mit Verbund-Datentyp):

Produkt := array(100) of structure{
    ProdNr := Text[6]                      // Text mit max. 6 Stellen
    Einkaufspreis := FixPunktZahl[4;2]     // Kommazahl mit 4 Stellen vor, 2 Stellen nach dem Komma
    Verkaufspreis := FixPunktZahl[4;2]     // dito
    Lagerbestand := Integer[6]             // Ganzzahl mit 6 Stellen
 } // end structure

Produkt(Index).ProdNr, Produkt(Index).Einkaufspreis liefern die genannten Werte für das Produkt, auf das der Index zeigt.

Mehrdimensional / in-sich-mehrdimensional

Mit dieser Variante lassen sich Informationen wie Elemente einer zweidimensionalen Fläche oder eines dreidimensionalen Würfels vorstellen. Dabei „beinhaltet nur die letzte Dimension die Elemente,“[10] jede Einzelinformation ist somit allen Dimensionen, z. B. Breite, Höhe, Tiefe, gleichermaßen zuzurechnen. Der Zugriff erfolgt unter Angabe aller Indizes ('<AttrName>(i1,i2,...)'). ISO_IEC 11404 nennt diese Felder unter den ‚General Purpose Datatypes‘ „inhärent mehrdimensional“. Diese mehrdimensionalen Felder werden, vor allem im Bereich des Deep Learning, nach ihrer mathematischen Entsprechung auch als Tensoren bezeichnet.[11]

Beispiele

1. zweidimensional (wie eine Matrix oder eine Tabelle):

In einer Matrix werden die waagerechten Einträge (Felder, Zellen) als Zeilen, die Senkrechten als Spalten bezeichnet. Ein einzelnes Element ist also durch Nennung von Zeile und Spalte eindeutig bezeichnet (adressiert). Üblich ist die Adressierung über ein Tupel (0,0) oder A1 für Spalte A, Zeile 1.

Schachfeld := array(8,8) of String

array deklariert Schachfeld als Array („Feld“) mit 8 mal 8 Einträgen, of deklariert den Typ des Eintrags, hier String.

 Schachfeld := (("w_Turm" ,"w_Springer","w_Läufer","w_König", … ,"w_Turm" ),
                ("w_Bauer","w_Bauer"   ,"w_Bauer" ,"w_Bauer", … ,"w_Bauer"),
                ("" target="_blank" rel="nofollow"       ,"" target="_blank" rel="nofollow"          ,"" target="_blank" rel="nofollow"        ,"" target="_blank" rel="nofollow"       , … ,"" target="_blank" rel="nofollow"       ),
                ("" target="_blank" rel="nofollow"       ,"" target="_blank" rel="nofollow"          ,"" target="_blank" rel="nofollow"        ,"" target="_blank" rel="nofollow"       , … ,"" target="_blank" rel="nofollow"       ),
                ("" target="_blank" rel="nofollow"       ,"" target="_blank" rel="nofollow"          ,"" target="_blank" rel="nofollow"        ,"" target="_blank" rel="nofollow"       , … ,"" target="_blank" rel="nofollow"       ),
                ("" target="_blank" rel="nofollow"       ,"" target="_blank" rel="nofollow"          ,"" target="_blank" rel="nofollow"        ,"" target="_blank" rel="nofollow"       , … ,"" target="_blank" rel="nofollow"       ),
                ("s_Bauer","s_Bauer"   ,"s_Bauer" ,"s_Bauer", … ,"s_Bauer"),
                ("s_Turm" ,"s_Springer","s_Läufer","s_König", … ,"s_Turm" ))

Die vorstehende Zuweisung legt die Start-Anordnung der Figuren fest, w_=weiß, s_=schwarz. D. h. oben sitzt der Spieler der weißen Figuren und unten der der schwarzen.

Im Beispiel läuft der Spaltenindex von links nach rechts, der Zeilenindex von oben nach unten. Im Folgenden sei der Zeilenindex der erste und der Spaltenindex der zweite Index, die Indizierung also Schachfeld[Zeilenindex,Spaltenindex]. Der Spaltenindex „läuft schneller“.

Beim Schach werden die Spalten als Linien bezeichnet und mit den Kleinbuchstaben „a“–„h“ adressiert, die Zeilen als Reihen, adressiert per „1“–„8“. Somit entspricht Schachfeld[z,s] dem Feld („a“–„h“)[9-s]z.

Die Beispielanweisungen Schachfeld[5,4]^*1 := Schachfeld[5,2]^*2 und Schachfeld[5,2]^*1 := "" target="_blank" rel="nofollow" liefern den Eröffnungszug „d2–d4“.

^{*1: oder [NachZeile,NachSpalte] *2: oder [VonZeile,VonSpalte]}

2. mehrdimensional (hier mit 4 Dimensionen):

Für einen Brennraum (x;y;z) (z. B. eines Motors),

wobei x, y und z in Millimeter jeweils von 1 bis 50 angegeben seien,

sei an jeder Stelle, und über den Zeitraum einer Sekunde für jede Millisekunde, eine Temperaturangabe gespeichert:

 temperatur := array(50,50,50,1000) of float

→ 4-dimensionales Array (x,y,z,zeit)

Wie heiß war es an der Stelle (x=7;y=12;z=48) zum Zeitpunkt t=617 ms?

 = temperatur( 7 , 12 , 48 , 617 )

Mehrdimensional / Feld enthält weiteres Feld

Hierbei enthält ein Feld als Element – neben meist anderen Datenfeldern – wiederum ein Feld usw. mit gegebenenfalls weiteren Stufen. Diese Variante wird auch verzweigtes Array genannt.[12][13] Im Feld gespeicherte Informationen gehören dabei jeweils zu genau einer Dimension, d. h. zu genau einer ihrer Indexausprägungen. Dementsprechend erfolgt der Zugriff auf Informationen im äußeren Feld zum Beispiel mit '<Attr_in_Dim1>(i)' und auf Informationen im inneren Feld mit '<Attr_in_Dim2>(i,j)' usw. „Mehrdimensional“ bezieht sich hier auf die Gesamtheit aller im Feld hierarchisch (= baumartig = ‚verzweigt‘) gespeicherten Informationen, nicht auf jedes einzelne Element. Die Anzahl der Dimensionen ergibt sich aus der „Schachtelungstiefe“ des innersten Arrays. ISO_IEC 11404 nennt diese Felder „induziert mehrdimensional“.

Beispiel ‚Felder für ein Lagerregal‘

 Lagerboden := array(10)                  // Es gibt 10 Lagerböden = Feld der 1. Dimension
   LB_Bezei := Text(20)                   //  wie der jeweilige Lagerboden genannt/beschriftet wird
   …                                      //  ggf. weitere Daten je Lagerboden, z. B. max. Gesamtgewicht
   WZ_Box := array(5)                     // Je Boden max. 5 Werkzeugboxen, 2. Dimension
     WZ_Bezei := Text(20)                 //  Bezeichnung der Werkzeuge, die in der Box gelagert bzw. zu lagern sind
     WZ_Anz := numeric(4)                 //  die Anzahl der darin gelagerten Werkzeuge
     …                                    //  ggf. weitere Daten je WZ-Box, u. U. weiteres Array 3. Dim.

'LB_Bezei (I1), "Box-Nr:" & I2, WZ_Bezei [I1,I2], WZ_Anz [I1,I2] ...' liefert die Werkzeug-Bezeichnung und ihre Anzahl, die in einer bestimmten Box (Lagerboden und Box-Nr) gelagert sind.

'LB_Bezei (I1)' liefert die Bezeichnung des Lagerbodens.

'WZ_Bezei (I1,I2) = "Rohrzangen", WZ_Anz (I1, I2) = 10' legt eine neue WZ-Box mit 10 Rohrzangen an.

'WZ_Anz (I1,I2) -1 aktualisiert die Anzahl bei Entnahme eines Werkzeugs aus der Box.

In den Anweisungen sind Indizes nur für die Dimension(en) anzugeben, aus denen Informationen angesprochen/abgerufen werden, z. B. LB_Bezei(x) oder WZ_Bezei(x,y).

Adressierung eines Feldes

Trotz der meist räumlich dargestellten Inhalte von Feldern, besonders bei mehrdimensionalen, werden auch die in einem Feld gespeicherten Elemente in einem linearen Speicher abgelegt. Die Elemente eines eindimensionalen Vektors werden hintereinander im Speicher abgelegt, bei einer zweidimensionalen Matrix werden die Elemente entweder als Zeilen- oder als Spaltenvektoren hintereinander abgelegt, bei einem dreidimensionalen Feld werden entsprechend viele Matrizen hintereinander abgelegt usw.

Bei den meisten Programmiersprachen wird das Adressieren von Feldern vollständig vom Compiler behandelt. In Assembler muss es im Quellcode explizit programmiert werden.

Speicherabbildungsfunktion

zwei Varianten der Anordnung eines zweidimensionalen Feldes im Hauptspeicher

Ein Programm, das auf Elemente eines Felds zugreifen will, muss deren Speicheradresse errechnen.

Beispiel

Gegeben: Ein 2-dimensionales Feld mit 4 Zeilen (1..4) und 7 Spalten (1..7). Jedes Element sei 4 Byte groß. Es soll zugegriffen werden auf das Element an (Zeile = 3, Spalte = 6). Das Feld beginne bei Speicheradresse base.

Da auf ein Element der Zeile 3 zugegriffen wird, müssen 2 Zeilen „übersprungen“ werden:

2 (Zeilen überspringen) * 7 (Elemente pro Zeile) * 4 (Byte pro Element) = 56 (= Beginn der 3. Zeile im Feld)

In der Zeile 3 soll auf Spalte 6 zugegriffen werden, also sind zusätzlich 5 Elemente zu „überspringen“:

5 (Spalten überspringen) * 4 (Byte pro Element) = 20 (= Beginn der 6. Spalte in Zeile 3)

Das gewünschte Element beginnt also an Adresse (base + 56 + 20) = (base + 76) und ist 4 Byte lang.

Allgemein

In einem $n$ -dimensionalen Feld $A[i_{1}:k_{1},i_{2}:k_{2},\ldots ,i_{n}:k_{n}]$ wird die Adresse eines Elements $a[j_{1},j_{2},..,j_{n}]$ beispielsweise mit Hilfe der Formel $(j_{n}-i_{n})+\sum _{s=1}^{n-1}((j_{s}-i_{s})\cdot \prod _{t=s+1}^{n}(k_{t}-i_{t}+1))$ berechnet. Man nennt diese Formel auch Speicherabbildungsfunktion.

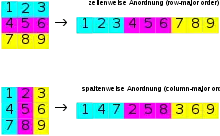
Die dargestellte Formel ist nur eine von mindestens zwei Alternativen, je nachdem, in welcher Reihenfolge die Indizes zu Speicherblöcken zusammengefasst werden, vom Ersten hin zum Letzten oder gerade umgekehrt. Im Englischen unterscheidet man hier Row-major order (zeilenweise Anordnung) und Column-major order (spaltenweise Anordnung).

Es ist normalerweise Sache der Laufzeitumgebung des jeweiligen Compilers, diese Berechnungen vorzunehmen und im jeweiligen Befehl zu verwenden, egal nach welcher Variante.

Dope-Vektor

Da die Produkte $\prod _{t=s+1}^{n}(\ldots )$ in obiger Formel konstant sind, können sie einmalig berechnet werden. Der daraus resultierende Dope-Vektor d ermöglicht anschließend über die Formel $\deg _{t=1}^{n}(j_{t}-i_{t})\cdot d_{t}$ eine sehr schnelle Berechnung der Adresse eines jeden gespeicherten Elements.

Programmeffizienz

Die Verarbeitung von Daten innerhalb eines Feldes erfordert – im Gegensatz zu ohne Index adressierbaren Datenfeldern – zusätzlichen Aufwand zur Berechnung der tatsächlichen Speicheradresse verwendeter Datenfelder. Die dazu nötigen, meist von einem Compiler erzeugten Berechnungsbefehle kann der Programmierer zum Teil beeinflussen und optimieren – sofern dies nicht bereits durch den Compiler geschieht. Die folgenden Beispiele nennen Details, deren Anwendung zu effizienterem Code führen kann, Details und weitere Beispiele siehe.[14]

Bei Literalen als Index berechnet der Compiler die Speicheradresse zur Compilezeit. Manche Compiler stellen fest, ob der Index von Variablen abhängt, deren Stand zur Compilezeit bereits bestimmt werden kann.
Verwenden von internen Datenformaten für die Indexvariable, damit im Rahmen der Adressierungsberechnung keine Formatkonvertierung erforderlich ist.
Wiederverwenden bereits berechneter Zugriffsadressen, anstatt sie für jeden Befehl erneut zu berechnen. Je nach Compiler können dazu geeignete Adressierungsmethoden gewählt werden, zum Teil stellen Compiler diese Wiederverwendung fest und erzeugen automatisch optimierten Code.
Eine geeignete Wahl der Reihenfolge der Dimensionen: Wenn in einem Computer ein Feld im RAM gehalten wird, erfolgen Zugriffe auf Feldelemente in der Regel am schnellsten, wenn direkt aufeinander folgende Adressen abgerufen werden (Lokalität ermöglicht Caching). Der Programmierer ist also gehalten, die Reihenfolge der Indizes im Feld so festzulegen, dass dies in der innersten Schleife ebenso erfolgt. Da die Speicherabbildungsfunktion vom Compiler abhängt, sollte sich der Programmierer über diese Details informieren und dann im Programm den in der innersten Schleife durchlaufenen Index so definieren, dass er im Ram aufeinanderfolgenden Elementen entspricht.
Auslagern von ‚Feld‘-Inhalten bei (ort-/zeitlokal) mehreren/vielen Zugriffen mit gleichem Index in einen eigenen, direkt adressierbaren Speicherbereich.
Übergeordnete Verbundstruktur ansprechen anstatt vieler elementarer Datenfelder: Zum Beispiel beim Verschieben von Array-Einträgen, etwa beim Sortieren von Array-Inhalten, findet die Adressberechnung bei Bezug auf einen Verbund (Verbundname(Index)) meist nur einmal je Verbund statt – dagegen bei Bezug auf einzelne Elemente des Verbunds je Verbund-Element.

Die Zweckmäßigkeit oder Notwendigkeit derartiger Effizienzmaßnahmen, die aus Gründen der Lesbarkeit eines Programms stets gut dokumentiert sein sollten, hängt von verschiedenen Faktoren ab: Nicht relevant sind sie, wenn der verwendete Compiler entsprechende Optimierungen automatisch vornimmt, weniger relevant zum Beispiel, wenn das Programm nur selten ausgeführt wird, wenn es jeweils nur eine kurze Laufzeit hat, wenn die Feld-bezogenen Befehle nur einen geringen Teil der Gesamtverarbeitung ausmachen.

Siehe auch

Weblinks

Wiktionary: Array – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Array-Datenstruktur – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Algorithmen und Datenstrukturen in C/ Felder – Lern- und Lehrmaterialien

Das Array, unendliche Weiten? – Dimensionen von Arrays; auf aspheute.com

Einzelnachweise

Programmieren in Fortran, Uni Bayreuth
Ein C-Tutorial. C-how-to
Microsoft msdn visual studio
linguee
rrzn Uni Hannover (PDF; 411 kB)
Beispiel für "heftige Diskussion" auf leo.org
msdn.microsoft.com Microsoft
www2.informatik.uni-halle.de (Memento des Originals vom 29. April 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Uni Halle
homeandlearn.co.uk Java
Programmersbase Tutorial / Java Grundlagen / Arrays (Memento vom 23. Februar 2015 im Internet Archive)
Jeff Dean, Rajat Monga, Sanjay Ghemawat: TensorFlow: Large-scale machine learning on heterogeneous systems. In: TensorFlow.org. Google Research. 11. September 2015. Abgerufen am 10. November 2015.
Rheinwerk-Verlag openbook.rheinwerk-verlag.de
MSDN msdn.microsoft.com
Maximierung der Codeperformance … MathWorks, Technical Articles and Newsletters

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Programmieren in Fortran, Uni Bayreuth

[2] Ein C-Tutorial. C-how-to

[MSDM-3] Microsoft msdn visual studio

[4] uee

[rrzn-5] rrzn Uni Hannover (PDF; 411 kB)

[6] Beispiel für "heftige Diskussion" auf leo.org

[7] sdn.microsoft.com Microsoft

[8] www2.informatik.uni-halle.de (Memento des Originals vom 29. April 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 Uni Halle

[9] rn.co.uk Java

[10] Programmersbase Tutorial / Java Grundlagen / Arrays (Memento vom 23. Februar 2015 im Internet Archive)

[whitepaper2015-11] Jeff Dean, Rajat Monga, Sanjay Ghemawat: TensorFlow: Large-scale machine learning on heterogeneous systems. In: TensorFlow.org. Google Research. 11. September 2015. Abgerufen am 10. November 2015.

[12] Rheinwerk-Verlag openbook.rheinwerk-verlag.de

[13] MSDN msdn.microsoft.com

[14] Maximierung der Codeperformance … MathWorks, Technical Articles and Newsletters