Schärfentiefe
Die Schärfentiefe (häufig auch Tiefenschärfe genannt) ist ein Maß für die Ausdehnung des scharfen Bereichs im Objektraum eines abbildenden optischen Systems. Der Begriff spielt in der Fotografie eine zentrale Rolle und beschreibt die Größe des Entfernungsbereichs, innerhalb dessen ein Objekt hinlänglich scharf abgebildet wird. In der Regel wird eine große Schärfentiefe durch kleine Blendenöffnungen oder Objektive mit kurzen Brennweiten erreicht: Von vorn bis hinten sieht dann alles mehr oder weniger scharf aus. Das Gegenteil ist der sogenannte „Film-Look“, bei dem der Bereich der Schärfentiefe klein ist (englisch: shallow): Die Kamera zeichnet die zentrale Figur scharf, eventuell nur das Auge einer Person,[1] während alles vor und hinter ihr unscharf erscheint. Tief bedeutet bei Schärfentiefe die Tiefe des Raums, also die Richtung weg von der Optik.




Die Schärfentiefe wird außer durch die Wahl der Brennweite und der Entfernungseinstellung auch durch die Blendenöffnung beeinflusst: je größer die Blendenöffnung (kleine Blendenzahl), um so geringer ist die Schärfentiefe (und umgekehrt). Bei einer Entfernungseinstellung (Fokussierung) auf ein nahes Objekt ist der optisch als scharf erfasste Objektraum von–bis kürzer als bei einer Fokussierung auf ein weiter entferntes Objekt. Die Wahl der Blendenöffnung ist Teil der Belichtungseinstellung.
In der Computeranimation ist die Schärfentiefe ein optischer Effekt, der im Nachhinein in jedes einzelne Bild eingerechnet wird und deshalb erheblichen Rechenaufwand bedeutet. Meist wird hier der englische Begriff depth of field (DOF) benutzt.
Umgangssprachlich werden Schärfentiefe und Tiefenschärfe synonym verwendet. Eine Normung des Begriffs „Schärfentiefe“ fand erstmals 1970 statt (DIN 19040-3). Die Abbildungstiefe stellt das Gegenstück zur Schärfentiefe auf der Bildseite dar.
Geometrische Schärfentiefe
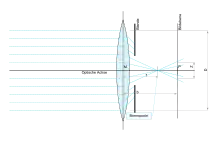
Es sind grundsätzlich zwei verschiedene Anordnungen zu unterscheiden: Die Camera obscura, die lediglich aus einer einzigen Lochblende besteht, und ein Linsensystem, das so eine Blende ebenfalls enthält, aber zusätzlich noch (mindestens) eine Linse (vor oder hinter der Blende), die eine reguläre optische Abbildung produziert.
Camera obscura
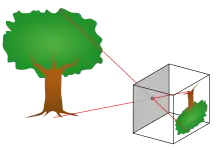
Von einem Objekt ausgehende Lichtstrahlen fallen durch die Lochblende auf die Bildebene (einen Schirm, einen Film oder einen Kamerabildsensor). Je nach Durchmesser der Blende werden aus diesen Lichtstrahlen mehr oder weniger dicke kegelförmige Lichtkörper. Durch Schnitt der Bildebene mit einem Kegel entsteht auf der Ebene ein Kreis, sogenannte Zerstreuungskreise oder Unschärfekreise (Z). Sie existieren bei jeder Dimensionierung der Abstände zwischen Objekt, Blende und Bild, die Kreisgröße in der Bildebene berechnet sich nach dem Strahlensatz. Dabei ist der Einfluss des Lochblendendurchmessers einfach proportional: Je größer das Loch, desto größer der Unschärfekreis. Für eine schärfere Abbildung wird ein kleineres Loch benötigt. Wird jedoch das Loch zu stark verkleinert, so wird der Bereich der geometrischen Optik verlassen und es treten die Welleneigenschaften des Lichtes in den Vordergrund. Die dabei auftretenden Beugungseffekte werden umso stärker, je kleiner das Loch ist. Hierdurch kommt es zu einer Abnahme der Schärfe. Somit gibt es für eine Camera obscura einen optimalen Lochdurchmesser. Weiterhin muss bei dieser Optimierung neben den Abbildungseigenschaften auch berücksichtigt werden, dass mit einem kleineren Lochdurchmesser der Lichtstrom abnimmt und damit die Belichtungszeiten zunehmen.
Linsensystem
Eine zusätzlich eingebaute Linse sorgt dafür, dass im idealen Fall bei einer bestimmten Entfernung der Bildebene von der Linse eine scharfe Abbildung auftritt. Bei dieser Position entfällt also die obige Ungenauigkeit und die Blendenöffnung kann im Interesse besserer Lichtausbeute wesentlich vergrößert werden. Erst wenn es um Objektpunkte geht, die vor oder hinter dieser scharf abgebildeten Position liegen, verringert sich diese Schärfe und sinkt mit wachsendem Abstand auf den Wert, den die Blende allein als Camera obscura bewirken würde. Genauer:
In der geometrischen Optik können nur diejenigen Punkte als scharfe Bildpunkte in der Bildebene (Film, Chip) wiedergegeben werden, die auf der Ebene liegen, die sich in der Gegenstandsweite zur Linse befindet. Alle anderen Punkte, die sich auf näher oder weiter entfernt liegenden Ebenen befinden, erscheinen in der Bildebene nicht mehr als Punkte, sondern als Scheibchen, sogenannte Zerstreuungs- oder Unschärfekreise (Z).
Zerstreuungskreise entstehen, weil die von der Linse (dem Objektiv) auf die Bildebene (den Film) fallenden Lichtkörper Kegel sind. Durch Schnitt der Bildebene mit einem Kegel entsteht auf der Ebene ein Kreis. Eng nebeneinander liegende Punkte, die nicht in der Gegenstandsebene liegen, werden durch eng nebeneinander liegende Zerstreuungskreise abgebildet, die sich überdecken und in den Randbereichen vermischen, wodurch ein unscharfes Bild entsteht.
Der für die Akzeptanz von Schärfe maximal tolerierbare Zerstreuungskreisdurchmesser für einen Fotoapparat wird mit bezeichnet. Die absolute Größe des maximalen Zerstreuungskreises ist abhängig vom Aufnahmeformat, da sie 1/1500 der Diagonalen beträgt. Solange die Unschärfekreise nicht größer als werden, liegen sie unterhalb der Auflösungsgrenze des Auges, und die Abbildung wird als scharf erachtet. Dabei entsteht der Eindruck, das Bild weise nicht nur eine Schärfenebene, sondern einen Schärfebereich auf. Problematisch wird ein eingeschränkter Schärfentiefebereich auch dann, wenn die Schärfemessung nicht direkt in der Bildebene, sondern mit gesonderten Einstellscheiben oder Schärfesensoren erfolgt, da es dann durch Toleranzen in der Bildweite leicht zu Fokussierungsfehlern kommen kann.
Die folgende Tabelle veranschaulicht die maximale Größe der Zerstreuungskreise je nach Aufnahmeformat des jeweiligen Fotoapparats:
| Aufnahmeformat | Abbildungsgröße | Seitenverhältnis | Bilddiagonale | Z | Normalbrennweite |
|---|---|---|---|---|---|
| 1/3″-Digitalkamera-Sensor | 4,4 mm × 3,3 mm | 4:3 | 5,5 mm | 3,7 µm | 6,4 mm |
| 1/2,5″-Digitalkamera-Sensor | 5,3 mm × 4,0 mm | 4:3 | 6,6 mm | 4,4 µm | 7,6 mm |
| 1/1,8″-Digitalkamera-Sensor | 7,3 mm × 5,5 mm | 4:3 | 9,1 mm | 6,1 µm | 10,5 mm |
| 2/3″-Digitalkamera-Sensor | 8,8 mm × 6,6 mm | 4:3 | 11,0 mm | 7,3 µm | 12,7 mm |
| MFT-Sensor | 17,3 mm × 13,0 mm | 4:3 | 21,6 mm | 14,4 µm | 24,9 mm |
| APS-C-Sensor | 22,2 mm × 14,8 mm | 3:2 | 26,7 mm | 17,8 µm | 30,8 mm |
| APS-C-Sensor | 23,7 mm × 15,7 mm | 3:2 | 28,4 mm | 19,2 µm | 32,8 mm |
| APS-H-Sensor | 27,9 mm × 18,6 mm | 3:2 | 33,5 mm | 22,4 µm | 38,7 mm |
| Kleinbildformat | 36 mm × 24 mm | 3:2 | 43,3 mm | 28,8 µm | 50,0 mm |
| Digitales Mittelformat | 48 mm × 36 mm | 4:3 | 60,0 mm | 40,0 µm | 69,3 mm |
| Mittelformat 4,5 × 6 | 56 mm × 42 mm | 4:3 | 70,0 mm | 46,7 µm | 80,8 mm |
| Mittelformat 6 × 6 | 56 mm × 56 mm | 1:1 | 79,2 mm | 52,8 µm | 91,5 mm |
| Großformate | z. B. 120 mm × 90 mm | z. B. 4:3 | z. B. 150 mm | 90–100 µm | z. B. 150 mm |
| Größere Formate | bis 450 mm × 225 mm | — | — | > 100 µm | — |
Schärfentiefe berechnen
Einfache Gleichung
Folgende Variablen werden benötigt:
- die Objektiv-Brennweite , zum Beispiel 7,2 mm
- die Blendenzahl gibt das Verhältnis von Brennweite zum Durchmesser der Eingangspupille an, zum Beispiel 5,6. Die Eingangspupille ist das virtuelle Bild der physischen Blende durch das gegenstandseitig vorgelagerte Linsensystem. Liegt die Blende vor dem gesamten Linsensystem, ist sie auch zugleich Eingangspupille. Weiter unten wird in den Formeln durch ersetzt. Während direkt vom Blendenring der Kamera abgelesen werden kann, ist ein um den Pupillenmaßstab korrigierter Wert:
- die Gegenstandsweite (Entfernung der fokussierten Gegenstandsebene von der vorderen Prinzipalebene), zum Beispiel 1000 mm
- der Durchmesser des Zerstreuungskreises , zum Beispiel 0,006 mm.
- der Abstand des Bildpunktes des Gegenstandes im Nah- bzw. Fernpunkt zur Bildebene der Einstellweite
Für eine Annäherung an kann folgende Formel mit als Formatdiagonale des Aufnahmeformates in mm und als Anzahl der zu unterscheidenden Punkte entlang der Diagonalen verwendet werden:
Dieser Näherung liegt die Annahme zugrunde, dass das menschliche Auge über die Bilddiagonale maximal 1500 Punkte auflösen kann, wenn der Sehabstand etwa gleich der Bilddiagonalen ist. Für technische Anwendungen mit höherer Bildauflösung muss gegebenenfalls deutlich höher gewählt werden.
Die Linsengleichung
für die vordere Hyperfokalebene und
für die hintere Hyperfokalebene. Insbesondere ergibt sich aus der Linsengleichung die Beziehung von Bildweite zur Gegenstandsweite:
- .
Geometrischen Überlegungen zum Zerstreuungskreis , dem Durchmesser der Austrittspupille und den Bildweiten und mit der Einstellbildweite und den Bildweiten der objektseitigen Fern- bzw. Nahpunkte und führen unter Berücksichtigung von mit
zu zwei Gleichungen:
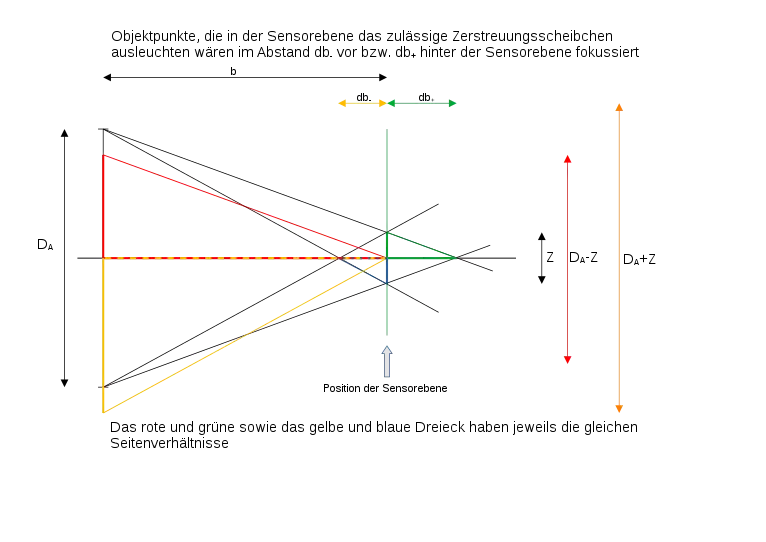
und man erhält:
- ,
so dass die Lösung für die Gegenstandsweite für den vorderen bzw. hinteren Hyperfokalpunkt lautet:
- .
Unter Zuhilfenahme von Hilfsvariablen lässt sich die Gleichung auflösen zu:
mit
Jetzt erhalten wir:
mit
- ,
dann erhalten wir für den Fern- bzw. Nahpunkt der Schärfentiefe:
- .
Somit ergibt sich:
Damit kann bei gegebener Gegenstandsweite der Nah- bzw. Fernpunkt bei gegebener Blende und Zerstreuungskreisrdurchmesser berechnet werden.
In die anfänglichen geometrischen Betrachtungen fließt implizit der Abbildungsmaßstab für die rectilineare bzw. gnomische Projektion ein: , wobei der Einfallswinkel des Lichtstrahles und der Abstand des Bildpunktes von der optischen Achse ist. Fisheyeobjektive arbeiten mit anderen Projektionen, um einen Öffnungswinkel von 180° zu erreichen, dies ist mit rectilinear abbildenden Objektiven nicht möglich. Prinzipiell gibt es mehrere Projektionen, die es erlauben einen Öffnungswinkel von 180° oder größer zu erreichen, eine Vielzahl der Fisheyeobjektive arbeiten mit der equisoliden Projektion: . Es gibt jedoch auch Objektive mit äquidistanter () und stereografischer Projektion (). Letzterer Typ ist sehr aufwendig und daher in der Regel auch verhältnismäßig teuer, hat aber den Vorteil, das die typischen Verzerrungen moderater ausfallen. Gemeinsam ist all diesen Objektiven jedoch, dass die Herleitung der Formel für die Schärfentiefe nicht oder nur eingeschränkt gültig ist. Eine notwendige Bedingung ist, dass die physische Blende sich entweder hinter dem Objektiv befindet (Blende ist gleich Austrittspupille), oder der bildseitige Teil des Objektivs die Blende gnomisch abbildet. Zudem gilt die Grundannahme für die Linsengleichung
aufgrund der andersartigen Projektionen nur näherungsweise in der Nähe der optischen Achse. Keinesfalls darf der Pupillenmaßstab vernachlässigt werden.
Aus dem Abbildungsmaßstab für die gnomische Projektion ergibt sich, dass die Ableitung der Funktion , nämlich die Winkelauflösung
- ,
eine Funktion des Einfallswinkels ist. Da die grundlegenden geometrischen Betrachtungen ganz offensichtlich (der Faktor 2 deutet auf Symmetriebedingungen hin) für Zerstreuungskreise in der optischen Achse formuliert wurden, muss der Frage nachgegangen werden, ob die Schärfentiefe eine Funktion des Einfallswinkels ist. Für beliebige Einfallswinkel gilt folgende Beziehung zwischen der Größe des Zerstreuungskreises und der der Austrittspupille:
- ,
was im Ergebnis den anfänglichen Überlegungen entspricht. Somit ist die Schärfentiefe vom Einfallswinkel unabhängig.
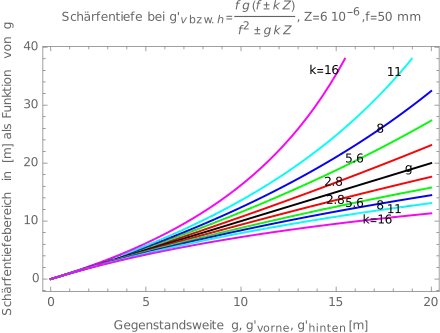
Hyperfokale Entfernung
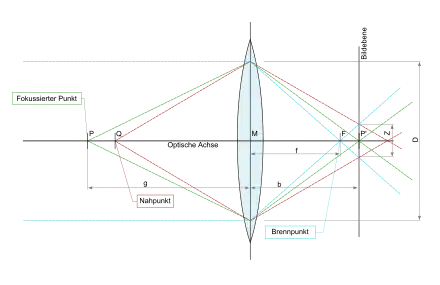
Für die nun folgenden Betrachtungen müssen wir uns darüber im Klaren sein, dass die Gegenstandsweite nicht die Entfernung eines realen Gegenstandes von der Hauptebene des Objektivs bezeichnet, sondern die Einstellweite am Objektiv für einen fiktiven Gegenstand. ist jedoch immer die Entfernung, aus der sich nach der Linsenformel die Bildweite ergibt.
Aus der Formel für den Fernpunkt des Schärfentiefenbereichs:
erkennt man, dass, wenn die Bedingung erfüllt ist, sich eine Singularität ergibt. Die Einstellweite , die diese Bedingung erfüllt nennt man Hyperfokaldistanz:
- .
Für den Spezialfall ergibt sich als Näherungsformeln:
Die Hyperfokaldistanz ist die Einstellweite, die den größten Schärfentiefebereich ergibt.
Nahpunkt
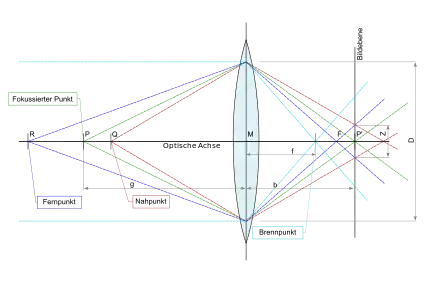
Für eine gegebene Einstellweite kann die Entfernung von der Hauptebene der Linse zum Nahpunkt berechnet werden zu:
Aus der Bedingung für die Singularität in der Formel für den Fernpunkt wissen wir:
- ,
so dass sich für eine Nahpunktdistanz von:
ergibt.
Der Nahpunkt liegt also bei der halben hyperfokalen Entfernung, und in diesem Fall werden Gegenstände von unendlich bis zur halben hyperfokalen Entfernung hinreichend scharf abgebildet. Die allgemeine Beziehung zwischen Nahpunkt und Einstellweite erhält man, wenn man die Kehrwerte von Nah- und Fernpunkt addiert:
- .
Für , was bedeutet, das die Einstellweite der Hyperfokaldistanz entspricht (), erhalten wir für den Nahpunkt wieder die halbe Einstellweite.
Eine weitere konkrete und praktisch relevante Frage ist die nach dem Gewinn an Schärfentiefe, wenn auf die hyperfokale Distanz fokussiert wird, anstatt auf eine unendliche Gegenstandsweite. Um diese Frage beantworten zu können, muss berechnet werden. Da das Rechnen mit Unendlichkeiten seine Tücken hat, wird die Gegenstandsweite substituiert durch: , sodass sich für den Nahpunkt folgende Formel ergibt:
- .
Mit: ergibt sich für den Nahpunkt:
- .
Durch fokussieren auf die Hyperfokaldistanz wird somit der Unschärfebereich nahezu halbiert.
Fernpunkt
In der Praxis wird sich recht häufig die Situation ergeben, dass eine Szene fotografiert werden soll, die sich über eine endliche Tiefe des Raumes erstreckt. Sodann stellt sich die Frage nach der optimalen Einstellweite , welche die größtmögliche Schärfentiefe für die gegebene Szene erzeugt. Für eine endliche Fernpunktdistanz
lässt sich durch Umformung und Auflösung der Gleichung nach die Einstellweite bestimmen. Über die Zwischenschritte:
- und
ergibt sich für die Einstellweite zunächst:
- .
Durch Erweiterung des Bruchs um ergibt sich:
und weiter:
Durch Multiplikation der Gleichung mit und Division durch ergibt sich dann:
Durch Substitution von durch die Hyperfokaldistanz ergibt sich dann die relativ übersichtliche Beziehung:
- ,
bzw. bei Gültigkeit der Aussage die Näherung:
- .
Eine besonders einfache Beziehung ergibt sich, wenn und in Einheiten von ausgedrückt werden ():
- .
Dieser Wert wird nie größer als eins, somit liegt die Einstellweite immer innerhalb der Hyperfokaldistanz.
Schärfentiefebereich
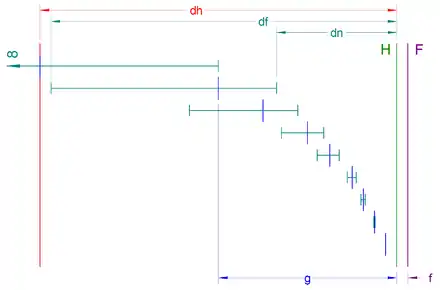
Der Schärfentiefebereich erstreckt sich vom Nahpunkt bis zum Fernpunkt mit
- ,
solange der Nenner positive Werte annimmt, was gleichbedeutend mit ist.
Wenn die eingestellte Gegenstandsweite größer oder gleich der hyperfokalen Entfernung ist (), dann ist der Schärfentiefebereich unendlich, da der Fernpunkt dann im Unendlichen liegt.
Wenn die eingestellte Gegenstandsweite gleich der Brennweite ist (), dann ist der Schärfentiefebereich null, da der Fernpunkt und der Nahpunkt identisch sind. Die Abbildung liegt dann im Unendlichen. Bei Makroaufnahmen mit entsprechend großen Abbildungsmaßstäben ergeben sich demzufolge meist recht kleine Schärfentiefebereiche.
Will man nun den Term durch ausdrücken, so ergibt sich:
- .
Sinnvolle Lösungen ergeben sich nur für , denn für wird der Nenner negativ mit der unsinnigen Konsequenz, dass der Nahpunkt in einer größeren Entfernung als der Fernpunkt liegen müsste.
Durch weitere Umformung der obigen Gleichung ergibt sich:
- .
Solange die Brennweite gegenüber der Einstellweite und der hyperfokalen Distanz vernachlässigt werden kann (), vereinfacht sich die Formel zu folgender Näherungsgleichung:
- .
Alternativ kann statt des Terms auch schon in der Formeln für den Fern- und Nahpunkt durch ausgedrückt werden. Über den Zwischenschritt
ergibt sich dann grundsätzlich in etwas schlankerer Herleitung das gleiche Ergebnis. Jedoch legt diese Herleitung nahe, für die Näherung von nur die Forderung zu stellen und auf eine Einschränkung der Einstellweite zu verzichten, so dass die Näherung für Einstellweiten gültig ist. Die Näherung ergibt sich dann zu:
- .
Zur Bestimmung der Güte der Näherung wird zunächst der relative Fehler aus dem Verhältnis des exakten Wertes zur Näherung gebildet:
- ,
und anschließend das Ergebnis für die Grenzfälle und betrachtet:
- und .
Das heißt, dass zum einen im Grenzfall die Näherung gegen den exakten Wert konvergiert und ihn für auch einnimmt. Zum anderen ergeben sich für den anderen Grenzfall Werte, die nach oben durch den relativen Fehler für die Näherungsformel der Hyperfokaldistanz beschränkt sind. Für ein Objektiv mit einer Brennweite von 50 mm ergibt sich unter der Annahme
ein maximaler relativer Fehler von 0,2%.
Generalisierter Formalismus
Ausgangspunkt zu einer generalisierten Betrachtung des Sachverhaltes sind wieder die Gleichungen für den Nah- und Fernpunkt des Schärfentiefebereichs. Indem die rechte Seite der Gleichung um den Faktor gekürzt wird ergibt sich:
Durch Normierung der Hyperfokaldistanz auf eins ergäbe sich für den Fernpunkt des Schärfentiefebereichs:
und unter der Annahme die Näherung
- .
Für den Nahpunkt ergibt sich leider eine etwas komplexere Relation, da die Brennweite im Nenner nicht verschwindet. Es erscheint daher sinnvoller zu sein, statt auf die Hyperfokaldistanz , auf deren Näherung zu normieren, was zulässig ist, da die Normierung frei gewählt werden kann.
- .
Die notwendige Annahme für die Näherung lautet nun aber: . Die Vereinfachung des Formalismusses wird also dadurch erkauft, dass die Näherung für kleine Gegenstandsweiten, insbesondere also für die Makrofotografie, nicht mehr gültig ist. Für den Nah- und Fernpunkt ergibt sich dann:
- und .
Für ergeben sich dann die bekannten Beziehungen:
- und .
Normierung auf die exakte Hyperfokaldistanz führt mit der Näherung für den Fernpunkt
unter Zuhilfenahme der allgemeinen Beziehung zwischen Nah- und Fernpunkt
ebenfalls zu der Näherung
- ,
nur wird unter dieser Herleitung die Einschränkung nicht offensichtlich.
Dieser generalisierte Formalismus, kann in einfacher Weise und unabhängig von Gerätekonstanten oder -einstellungen genutzt werden. Für den Schärfentiefenbereich ergibt sich nun:
- .
Ein Ergebnis, welches bereits oben hergeleitet wurde, jedoch nicht in dieser puristischen Form.
Ebenso einfach lassen sich nun die Bereiche der Schärfentiefe vor und hinter der Gegenstandsweite berechnen:
- und
- .
Es ist zu beachten, dass durch die Normierung alle Größen dimensionslos sind. Um metrische Größen zu erhalten, müssen resultierende Längen mit der Hyperfokaldistanz multipliziert werden.
Das Verhältnis der Schärfenbereiche vor und hinter der Gegenstandsweite ergibt sich dann zu:
- .
Für kleine Gegenstandsweiten (, d. h. die Gegenstandsweite ist klein im Verhältnis zur Hyperfokaldistanz) erstreckt sich der Schärfebereich etwa zu gleichen Teilen vor und hinter der Gegenstandsweite. Mit zunehmender Gegenstandsweite divergiert das Verhältnis sehr schnell und für (Gegenstandsweite größer der Hyperfokaldistanz) gibt es keine sinnvollen Lösungen mehr, da der Fernpunkt des Schärfebereiches dann im Unendlichen liegt. Da sich für die Fern- und Nahpunktdistanz das gleiche Verhältnis ergibt gilt:
Wird diese Gleichung nach aufgelöst, erhält man die Einstellweite, die bei gegebener Nah- und Fernpunktdistanz den kleinsten Blendenwert bzw. die größte Blendenöffnung ermöglicht, mit dem der Bereich zwischen dem Nah- und Fernpunkt hinreichend scharf abgebildet werden kann:
- .
Die optimale Einstellweite ergibt sich also aus dem harmonischen Mittel aus Nah- und Fernpunktdistanz. Da durch die Mittelwertbildung Normierungsparameter eliminiert werden, ergibt sich das Resultat bei Verwendung metrischer Eingangsdaten direkt im metrischen System.
Bei genauer Betrachtung der Beziehung zwischen Gegenstandsweite und Fernpunkt einerseits
und Nahpunkt und Gegenstandsweite andererseits
ist die Ähnlichkeit der Beziehungen augenfällig. Insbesondere erkennt man, dass bei Verringerung der Einstellweite auf die Entfernung des bisherigen Nahpunktes, der neue Fernpunkt in der Entfernung der bisherigen Gegenstandsweite liegt. Es ergibt sich also für jede Fernpunktdistanz eine Folge subsequenter Schärfentiefebereiche mit:
- und .
Speziell ergibt sich für den Fall die Folge
- .
Durch den generalisierten Formalismus konnte die Komplexität der Formeln drastisch reduziert werden, durch die Elimination der Objektivparameter ist es aber nicht mehr möglich, deren Einfluss auf die Schärfenteife zu diskutieren.
Makrofotografie
In der Makrofotografie ist das Ziel ein Objekt sehr groß und detailliert wiederzugeben. Speziell zu diesem Zweck gerechnete Objektive erreichen oft einen Abbildungsmaßstab von 1:1, d. h. das Bild auf dem Sensor/Film entspricht der Größe des abgebildeten Objektes. Die Gegenstandsweite liegt dann in der Größenordnung der Brennweite. Aus der Linsengleichung ergibt sich, dass bei einem Abbildungsmaßstand von 1:1 die Gegenstandsweite exakt das doppelte der Brennweite beträgt.
Der Abbildungsmaßstab
bestimmt das Verhältnis von Gegenstandsweite zur Bildweite und somit über die Linsenformel die Relation zwischen Gegenstandsweite und Brennweite:
- .
Somit kann der Term durch substituiert werden. Für die Schärfentiefe ergibt sich dann die Beziehung:
- .
Solange die Ungleichung gilt, kann der zweite Term im Nenner vernachlässigt werden und es ergibt sich folgende Näherung:
- .
Für die Makrofotografie ergibt sich somit eine gute Näherung für die Schärfentiefe, die keine explizite Abhängigkeit von der Brennweite enthält und stattdessen vom Abbildungsmaßstab abhängt.
Für den Abbildungsmaßstab von 1:1 vereinfacht sich die Formel zu: . Somit ergibt sich für eine Vollformatkamera mit einem Zerstreuungskreis 0,0288 mm bei einem Blendenwert von 8 eine Schärfentiefe von ca. 1 mm.
Unter diesen und der zusätzlichen Annahme, das Makroobjektive habe eine Brennweite von 100 mm ergibt sich eine relative Abweichung von der exakten Formel von .
Andererseits kann durch substituiert werden. Durch anschließende Multiplikation des Zählers und Nenners mit ergibt sich:
- .
Mit kann gegenüber und gegenüber vernachlässigt werden und folgende Näherung ist für den Bereich der Makrofotografie gut erfüllt:
- .
Außerhalb der Makrofotografie ergibt sich für hinreichend kleine Abbildungsmaßstäbe () eine Vereinfachung zu:
- .
Eine für zu vermutende annähernd reziproke quadratische Abhängigkeit der Schärfentiefe vom Parameter ist praktisch nicht gegeben, da mit steigendem sehr schnell der durch die Näherung verursachte Fehler wächst (siehe unten).
Für die hier angenommenen sehr kleinen Abbildungsmaßstäbe () gilt die Näherung , daraus folgt: .
Zur exakten Bestimmung von wird aus den obigen Formeln für folgende Beziehung extrahiert:
- .
Durch Kürzen und Multiplikation mit der Beziehung ergibt sich:
- .
Durch geeignete mathematische Umformung, indem
gesetzt wird und anschließendem Kürzen ergibt sich:
- .
Wenn die Einstellweite der Hyperfokalen Entfernung entspricht gelten die beiden folgenden Bedingungen: und . Somit ergibt sich aus obiger Beziehung:
und für den Abbildungsmaßstab in der Hyperfokaldistanz:
- .
Die Sensordiagonale als Parameter
Aus der Näherungsformel für die hyperfokale Entfernung kann leicht abgelesen werden, dass diese zunimmt und der Schärfentiefebereich somit abnimmt, wenn die Brennweite zunimmt, die Blendenzahl kleiner wird (respektive die Blendenöffnung größer) oder der Zerstreuungskreis kleiner sein soll.
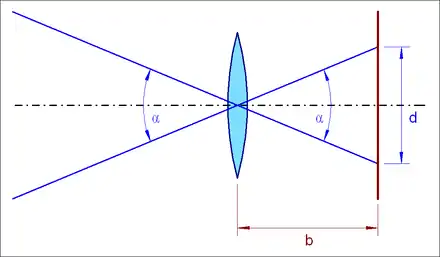
Möchte man nun die hyperfokale Entfernung nach der Bilddiagonale parametrisieren liegt mit Hinblick auf den Cropfaktor die Vermutung nahe, dass das Verhältnis zwischen Brennweite und Sensordiagonale eine Konstante ist, solange der Öffnungswinkel der Abbildung sich nicht ändert. Die detaillierte Betrachtung geht von der Formel für die gnomische bzw. rectilineare Projektion aus, die das Verhältnis zwischen Einfallswinkel des Lichtes und Abstand des Bildpunktes von der optischen Achse beschreibt. Für einen Bildkreis mit Öffnungswinkel (wobei der gewünschte Bildwinkel ist, der für die perspektivische Bildwirkung maßgeblich ist) ergibt sich die Beziehung:
Es ist zu beachten, dass sich bei einer Fokussierung auf die Bildweite der Abstand zwischen Objektiv und Sensor ändert, und somit auch der Öffnungswinkel der Abbildung. Ein Ansatz, der von einer Beziehung zwischen und ausgeht, steht also im Widerspruch zu den Eingangsvoraussetzungen. Setzt man dies in die Gleichung für die hyperfokale Entfernung ein, ergibt sich:
bzw. für ergibt sich die Näherung:
Dies bedeutet, dass die hyperfokale Entfernung linear mit der Bilddiagonalen zunimmt, wenn die Blendenzahl , die Anzahl der Bildpunkte auf der Bilddiagonalen und der Bildwinkel konstant gehalten werden. Ebenso kann der Formel abgelesen werden, dass die Schärfentiefe desto geringer ist, je kleiner die Blendenzahl oder der Bildwinkel sind. Weitwinkelobjektive haben also bei sonst gleichen Voraussetzungen einen größeren Schärfentiefebereich als Teleobjektive, beziehungsweise die hyperfokale Entfernung ist bei Weitwinkelobjektiven kleiner als bei Teleobjektiven.
Ferner kann festgehalten werden, dass die Schärfentiefe bei konstantem Verhältnis von Bildsensordiagonale und Blendenzahl bei gleichem Bildwinkel und gleicher Anzahl der akzeptablen Zerstreuungskreise immer gleich ist.
Aufeinanderfolgende Schärfentiefebereiche
Verringert man die Einstellweite derart, dass der Fernpunkt des Schärfentiefenbereichs der Hyperfokaldistanz entspricht ergibt sich eine interessante Reihe subsequenter Schärfentiefebereiche. Ausgangspunkt der Betrachtung ist, dass eine Verringerung der Einstellweite auf zum gewünschten Ergebnis führt, dann wird beim q-fachen der Einstellweite der Nenner in der Formel für die Distanz zum Fernpunkt Null und es ergibt sich folgende Beziehung:
und daraus folgt:
- ,
wobei die Näherung unter der Bedingung gültig ist. Das heißt, dass die neue Einstellweite annähernd der halben Hyperfokaldistanz entspricht, also in der Distanz des ehemaligen Nahpunktes liegt. Indem der Vorgang j-fach wiederholt wird ergibt sich:
und daraus wieder:
- .
Oder:
- .
Die Distanz zum Nahpunkt ergibt sich dann aus der Distanz zum Fernpunkt zu:
- ,
wobei der zusätzliche Term im Nenner eine weiter Näherung erfordert: , dies ist im Bereich der Makrofotografie ganz offensichtlich nicht mehr gegeben, für den Abbildungsmaßstab ergibt sich das Verhältnis zu:
- .
Somit ergibt sich für ganzzahlige eine Folge von Schärfentiefenbereiche, deren Fernpunkte annähernd bei und deren Nahpunkte annähernd bei liegen, wenn auf eine Entfernung von fokussiert wird.
Die Gültigkeit der Näherung wird mit steigendem j jedoch schnell eingeschränkt, da sich der Fehler ständig aufsummiert:
- .
Für eine Vollformatkamera mit einem dort gängigen Normalobjektiv () liegt der Faktor vor der Summe bei einer eingestellten Blende von 8 bei ca. 0,005, das heißt die Summe muss deutlich kleiner bleiben als 200, sie wächst aber stetig. Die Summe kann leicht aus den Näherungswerten der berechnet werden, da sich für die ganzzahlige positive Werte ergeben:
- .
Wird der akzeptable Fehler auf 10% beschränkt, darf der Wert der Summe 20 nicht übersteigen. Das Ergebnis für liegt dann schon außerhalb des akzeptablen Bereichs.
Mit
ergibt sich wieder die Näherung die weiter oben schon mal hergeleitet wurde. Mit der hier gegebenen Fehlerbetrachtung wurde gezeigt, dass die Näherung nur eingeschränkt anwendbar ist.
Beispiel Kurzsichtigkeit
Wenn das Auge eines Normal- oder Weitsichtigen auf die hyperfokale Entfernung scharfgestellt ist, wird der Bereich von der halben hyperfokalen Entfernung bis unendlich hinreichend scharf abgebildet und wahrgenommen. Anders ist es bei Kurzsichtigen, die aufgrund ihrer Kurzsichtigkeit nur bis zu einer maximalen Entfernung scharfstellen können und die hyperfokale Entfernung daher oft nicht erreicht werden kann.
Für die Berechnung wurde eine normale Brechkraft des Auges von 59 Dioptrien angenommen. Daraus resultiert eine Normalbrennweite von 16,9 Millimetern und ein Bildkreisdurchmesser von 14,6 Millimetern. Wenn für die Anzahl der Punkte auf der Bilddiagonalen 1500 angenommen wird, dann beträgt der Durchmesser des akzeptablen Zerstreuungskreises 9,74 Mikrometer. Bei unkorrigierter Kurzsichtigkeit kann das Auge nur auf eine maximale Gegenstandsweite scharfstellen, die sich mit Hilfe der Abbildungsgleichung aus der tatsächlichen Brechkraft ergibt, die üblicherweise als negative Dioptriendifferenz angegeben wird:
In der folgenden Tabelle werden die Schärfentiefebereiche beispielhaft für drei verschiedene Lichtsituationen respektive Blendenzahlen für das Auge dargestellt:
- Blendenzahl : weite Pupille (Durchmesser = 4,2 Millimeter in dunkler Umgebung)
- Blendenzahl : mittlere Pupille (Durchmesser = 2,1 Millimeter in mittlerer Umgebung)
- Blendenzahl : kleine Pupille (Durchmesser = 1,1 Millimeter in heller Umgebung)
Wenn der Fernpunkt unendlich erreicht, ist das Auge auf die hyperfokale Entfernung fokussiert und es ist zum scharfen Sehen gar nicht mehr nötig noch größere Entfernungen scharfzustellen.
| Fehlsichtigkeit in dpt | 0 | −0,25 | −0,5 | −0,75 | −1 | −1,5 | −2 | −3 | −5 | −10 | |
| Brennweite in m | 0,0169 | 0,0169 | 0,0168 | 0,0167 | 0,0167 | 0,0165 | 0,0164 | 0,0161 | 0,0156 | 0,0145 | |
| Blendenzahl | |||||||||||
| Hyperfokale Entfernung in m | 4 | 7,39 | 7,33 | 7,27 | 7,21 | 7,15 | 7,03 | 6,91 | 6,69 | 6,28 | 5,41 |
| Maximale Gegenstandsweite in m | 4 | 7,39 | 4,00 | 2,00 | 1,33 | 1,00 | 0,67 | 0,50 | 0,33 | 0,20 | 0,100 |
| Nahpunkt in m | 4 | 3,70 | 2,59 | 1,57 | 1,13 | 0,88 | 0,61 | 0,47 | 0,32 | 0,19 | 0,098 |
| Fernpunkt in m | 4 | ∞ | 8,76 | 2,75 | 1,63 | 1,16 | 0,73 | 0,54 | 0,35 | 0,21 | 0,102 |
| Schärfentiefe in m | 4 | ∞ | 6,17 | 1,18 | 0,50 | 0,28 | 0,12 | 0,07 | 0,03 | 0,01 | 0,003 |
| Hyperfokale Entfernung in m | 8 | 3,70 | 3,67 | 3,64 | 3,61 | 3,58 | 3,52 | 3,47 | 3,35 | 3,15 | 2,71 |
| Maximale Gegenstandsweite in m | 8 | 3,70 | 3,67 | 2,00 | 1,33 | 1,00 | 0,67 | 0,50 | 0,33 | 0,20 | 0,100 |
| Nahpunkt in m | 8 | 1,86 | 1,84 | 1,29 | 0,98 | 0,78 | 0,56 | 0,44 | 0,30 | 0,19 | 0,097 |
| Fernpunkt in m | 8 | ∞ | ∞ | 4,39 | 2,10 | 1,38 | 0,82 | 0,58 | 0,37 | 0,21 | 0,103 |
| Schärfentiefe in m | 8 | ∞ | ∞ | 3,10 | 1,12 | 0,59 | 0,25 | 0,14 | 0,06 | 0,02 | 0,006 |
| Hyperfokale Entfernung in m | 16 | 1,86 | 1,84 | 1,83 | 1,81 | 1,80 | 1,77 | 1,74 | 1,69 | 1,58 | 1,36 |
| Maximale Gegenstandsweite in m | 16 | 1,86 | 1,84 | 1,83 | 1,33 | 1,00 | 0,67 | 0,50 | 0,33 | 0,20 | 0,100 |
| Nahpunkt in m | 16 | 0,93 | 0,93 | 0,92 | 0,77 | 0,65 | 0,49 | 0,39 | 0,28 | 0,18 | 0,094 |
| Fernpunkt in m | 16 | ∞ | ∞ | ∞ | 4,86 | 2,21 | 1,05 | 0,69 | 0,41 | 0,23 | 0,107 |
| Schärfentiefe in m | 16 | ∞ | ∞ | ∞ | 4,09 | 1,56 | 0,57 | 0,30 | 0,13 | 0,05 | 0,013 |
Wellenoptische Schärfentiefe
Alle optischen Abbildungen sind durch Beugung begrenzt, so dass ein einzelner Punkt niemals auf einen Punkt, sondern nur auf ein Beugungsscheibchen (oder Airyscheibchen) abgebildet werden kann. Die Trennschärfe zweier benachbarter Beugungsscheibchen definiert analog zum fotografischen Film einen maximal zulässigen Zerstreuungskreis. Nach dem Rayleigh-Kriterium muss die Intensität zwischen zwei benachbarten Bildpunkten um 20 Prozent abfallen, um als scharf zu gelten. Die Größe des Beugungsscheibchens ist abhängig von der Wellenlänge des Lichts. Man definiert die Rayleighsche Schärfentiefe als den Bereich, innerhalb dessen sich die Abbildungsgröße nicht ändert, das heißt konstant dem kleinstmöglichen (d. h. beugungsbegrenzten) Wert entspricht:
Hierbei ist die Wellenlänge, n der Brechungsindex und u der Aperturwinkel des abbildenden Systems.
Die Rayleighsche Schärfentiefe ist bei beugungsbegrenzten optischen Systemen relevant, zum Beispiel in der Mikroskopie oder in der Fotolithografie. In der Fotografie macht sich eine wellenoptische Unschärfe jenseits der förderlichen Blende bildwirksam bemerkbar.
Hierbei ist der maximal zulässige Zerstreuungskreis, der Abbildungsmaßstab und die Wellenlänge.
Für übliche Anwendungen (kleiner Abbildungsmaßstab) in der Kleinbild-Fotografie ergibt sich eine förderliche Blende von über f/32, so dass Beugung außer in der Makrofotografie kaum eine Rolle spielt.
Da die kleinen Sensoren moderner Kompakt-Digitalkameras aber sehr kleine zulässige Zerstreuungskreise erfordern, rückt in den Bereich üblicher Blendenzahlen. Für einen 1/1,8″-Sensor liegt die förderliche Blende zum Beispiel bei zirka f/8, im Nahbereich noch darunter.
Lochkamera
Bei rein strahlenoptischer Betrachtungsweise hängt die Größe des Unschärfekreises einer Lochkamera von der Gegenstandsweite , der Bildweite und dem Lochdurchmesser ab. Ein Objekt wird dann hinreichend scharf abgebildet, wenn gilt:
Für sehr große Gegenstandsweiten vereinfacht sich die Bedingung zu: . Das heißt, der Lochdurchmesser darf nicht größer werden als der zulässige Zerstreuungskreisdurchmesser, sonst ist mit einer Lochkamera auch im Fernbereich keine hinreichend scharfe Abbildung mehr möglich.
Aus der wellenoptischen Betrachtungsweise lässt sich aus dem Rayleigh-Kriterium für die Beugung an einer Lochblende folgender Zusammenhang zwischen Unschärfekreis und Lochdurchmesser ableiten.
Der optimale Wert für den Lochdurchmesser ergibt sich dann aus der Beziehung.
zu:
bzw.
- .
Der optimale Lochdurchmesser nimmt also für unendliche Gegenstandsweiten () seinen maximal möglichen Wert an:
Sowohl unter wellen- als auch unter strahlenoptischer Betrachtungsweise ergibt sich für sehr große Gegenstandsweiten somit , d. h., sofern der Zerstreuungskreisdurchmesser größer ist als der Durchmesser des Unschärfekreises , liegt der Fernpunkt des Schärfentiefebereichs immer im Unendlichen, ansonsten gibt es keine optimal scharfe Darstellung. Mit zunehmenden sinkt der optimale Lochdurchmesser:
und der zugehörige Unschärfekreis steigt im gleichen Maß: .
Das gleiche Ergebnis resultiert aus folgender Betrachtung: Unter Zuhilfenahme zweier Konstanten und und Addition der wellenoptischen und strahlenoptischen Unschärfen ergibt sich:
- .
Die Extremwerte dieser Funktion ergeben sich durch differenzieren und anschließender Nullstellenbestimmung:
und aus
folgt dann:
- .
Dies entspricht exakt dem obigen Ergebnis. Da
- ,
handelt es sich bei dem Extremum um ein Minimum.
Aus dem minimal möglichen Unschärfekreis lässt sich nun die notwendige Bilddiagonale bestimmen (siehe oben) und es ist unmittelbar ersichtlich, dass Lochkameras riesige Dimensionen annehmen müssen. Unter der Annahme, dass die Bildweite in etwa der Bilddiagonalen entsprechen sollte, liegen deren Werte in der Größenordnung eines Meters.
Anwendung in der Fotografie






Bildgestaltung mit Schärfentiefe
Der gezielte Einsatz der Schärfentiefe durch Einstellen der Blendenzahl, der Entfernung und der Brennweite ermöglicht es, den Blick des Betrachters auf das Hauptmotiv zu lenken. Dazu schränkt der Fotograf die Schärfentiefe so eng wie möglich um die Ebene ein, auf der sich das Hauptmotiv befindet. Der Vorder- und Hintergrund wird dadurch unscharf abgebildet. Diese selektive Unschärfe lenkt weniger vom Hauptmotiv ab, das durch die selektive Schärfe akzentuiert wird.
Eine eingeschränkte Schärfentiefe kann bei fotografischen Aufnahmen mit punktförmigen Objekten, die sich etwas außerhalb der scharf abgebildeten Gegenstandsweite befinden, zu sogenannten Geisterflecken in der Aufnahme führen.
Bei kleinen Aufnahmeformaten, z. B. beim Erstellen von Ausschnittsvergrößerungen oder beim Einsatz von Digitalkameras mit kleinen Bildsensoren (Formatfaktor), verkleinert sich der maximal zulässige Zerstreuungskreis, was den Schärfentiefebereich zunächst verkleinert. Die kleineren Aufnahmeformate erfordern jedoch proportional kleinere Objektivbrennweiten, um gleichbleibende Blickwinkel zu gewährleisten – das hingegen vergrößert den Schärfentiefebereich. Beides, die Verkleinerung der Bildsensoren (⇒ Verkleinerung der maximal zulässigen Zerstreuungskreise) und die deshalb notwendige Verkleinerung der Objektivbrennweiten, beeinflusst den Schärfentiefebereich. Die Einflüsse sind zwar gegensinnig, sie gleichen sich aber nicht aus. Der maximal zulässige Zerstreuungskreis geht linear und die Objektivbrennweite annähernd quadratisch in die Schärfentiefe ein – also überwiegt der Einfluss der Objektivbrennweite. Dadurch wird die Schärfentiefe entsprechend größer und es wird zunehmend schwieriger, die selektive Schärfe als fotografisches Gestaltungsmittel direkt beim Fotografieren einzusetzen.
Wird der Unschärfebereich als gestalterisches Mittel der Bildkomposition genutzt, stellt sich schnell die Frage nach der Beeinflussung der Größe der Unschärfekreise durch die gewählten Belichtungsparameter und der fotografischen Ausrüstung. Die Abhängigkeiten werden beschrieben, indem die Gleichung für den Fernpunkt des Schärfebereiches nach aufgelöst wird.
Der Unschärfekreis wurde mit einem indiziert, um kenntlich zu machen, dass es sich hier nicht um den maximal zulässigen Zerstreuungskreis handelt, der sich aus der Bilddiagonalen und dem optischen Auflösungsvermögen des Auges bestimmt. Die Gegenstandsweite wurde mit dem Index gekennzeichnet, da sie hier die Einstellweite darstellt, auf die das Objektiv fokussiert wurde. bezeichnet die Gegenstandsweite eines Lichtpunktes, der außerhalb des Schärfentiefebereichs liegt und mit dem Durchmesser auf dem Sensor abgebildet wird. Es ist offensichtlich, dass sich für
als exakte Lösung ergibt und für hinreichen große , also als zulässige Näherung:
- .
Um bei der Bildgestaltung im Hintergrund große Unschärfekreise zu erhalten, sind Lichtstarke Objektive mit langer Brennweite und geringer Nahgrenze vorteilhaft.
| Objektiv | Brennweite | Lichtstärke | Nahgrenze | max. Unschärfekreisdurchmesser |
|---|---|---|---|---|
| Steinheil Cassar | 50 mm | f/2,8 | 0,9 m | 1,05 mm |
| Domiplan | 50 mm | f/2,8 | 0,75 m | 1,27 mm |
| Tair 11A | 135 mm | f/2,8 | 1,2 m | 6,11 mm |
| Carl Zeiss Pancolar | 50 mm | f/1,8 | 0,35 m | 4,63 mm |
| Helios 44-6 | 58 mm | f/2 | 0,5 m | 3,81 mm |
| Zenitar-N | 50 mm | f/1,2 | 0,45 m | 5,21 mm |
Da diese Unschärfekreise auf allen Sensoren gleich groß sind, Fotos von Kameras mit kleinen Sensoren jedoch stärker vergrößert werden müssen, um die üblichen Betrachtungsformate zu erhalten, erhält man am Ende mit kleinen Sensoren grundsätzlich größere Unschärfekreise. Dies gilt jedoch nicht, wenn der Bildwinkel erhalten bleiben soll. Dann gilt, dass das Verhältnis von Brennweite zu Sensordiagonalen konstant sein muss. Da die Brennweite aber quadratisch in den Durchmesser des Unschärfekreises eingeht, erhält man mit großen Sensoren dann die größeren Unschärfekreise.
In der Makrofotografie wird durch den Abbildungsmaßstab substituiert und es ergibt sich:
- .
Als Spezialfall für ergibt sich dann:
- .
Somit entspricht dann die Größe des Unschärfekreises dem Durchmesser der Eintrittspupille.
Faktoren zur Beeinflussung der Schärfentiefe
.gif)
Der Schärfebereich kann durch mehrere Faktoren (siehe Abschnitt Schärfentiefe berechnen) beeinflusst werden:
- Durch Abblenden der Blende wird er ausgedehnt und durch Aufblenden eingeengt. Je kleiner die Blendenöffnung ist, desto größer ist also der Schärfebereich.
- Eine weitere Einflussgröße auf die Schärfentiefe ist der Abbildungsmaßstab . Der Abbildungsmaßstab hängt von der Brennweite des Objektivs und der Gegenstandsweite ab ( ist die Bildweite).
- Je kleiner der Abbildungsmaßstab, desto größer ist die Schärfentiefe. Ein Weitwinkelobjektiv mit einer kürzeren Brennweite erzeugt, bei gleicher Gegenstandsweite, eine größere Schärfentiefe als ein Teleobjektiv mit einer langen Brennweite.
- Für Kamerasysteme mit unterschiedlichen Bilddiagonalen und somit entsprechend unterschiedlichen Normalbrennweiten gilt bei sonst gleichen Voraussetzungen (Blendenzahl, Bildwinkel und Bildauflösung), dass die Schärfentiefe umso geringer wird, je größer die Bilddiagonale ist. Es ist also mit größeren Kameras bei gegebener Blendenzahl besser möglich, die Schärfentiefe einzuschränken (etwa bei Porträtaufnahmen mit unscharfem Hintergrund), als mit kleinen Kameras. Wenn ein Motiv einmal so aufgenommen wird, dass es auf dem Sensor die Sensorhöhe voll ausfüllt, und einmal so, dass es auf dem Sensor eine um den Faktor geringere Höhe hat, indem man lediglich den Abstand zum Motiv vergrößert, so vergrößert sich die Schärfentiefe unter etwa quadratisch mit . Beispiel: Verkleinerung der Bildhöhe um den Faktor führt etwa zur Vervierfachung der Schärfentiefe. Diese Faustformel gilt, falls die Entfernung zum Motiv kleiner als etwa ein Viertel der hyperfokalen Entfernung ist. Entsprechend gilt diese Faustformel für unterschiedliche Sensorgrößen: Eine Verringerung der Sensorhöhe um den Faktor führt zur Vergrößerung der Schärfentiefe etwa um den Faktor , falls das Motiv in beiden Fällen die Sensorhöhe voll ausfüllt und in beiden Fällen die gleiche Blende eingestellt ist. Die Brennweite hat dabei keinen nennenswerten Einfluss, siehe unten.
- Anders sieht der eher akademische Vergleich verschiedener Kamerasysteme mit unterschiedlichen Bilddiagonalen aus, wenn man nicht Objektive mit gleicher Blendenzahl, sondern solche mit der gleichen Eintrittspupille vergleicht, also Objektive, die das gleiche, von einem Gegenstandspunkt ausgehende Lichtbündel auf einen Bildpunkt projizieren. Die Proportionalität zwischen der Sensordiagonalen und der Brennweite: wurde bereits gezeigt. Solange die Näherung gilt, ergibt sich für die hyperfokale Distanz: , wobei der Pupillenmaßstab ist. Dies bedeutet, zwei Objektive mit gleicher Eintrittspupille und gleichem Bildwinkel erzeugen unabhängig von der Sensorgröße die gleiche Schärfentiefe, solange der Pupillenmaßstab identisch ist. Diese Betrachtung ist insofern akademisch, als dass sie für Zoomobjektive kaum Anwendung findet, da sich der Pupillenmaßstab durch das Verschieben der Linsengruppen zueinander in der Regel ändert und andererseits kaum zwei Objektive zu finden sein werden, die die Bedingungen erfüllen.
- Die Verteilung der Schärfentiefe vor und hinter dem fokussierten Objekt variiert mit der eingestellten Entfernung: Im engen Nahbereich wird ungefähr ein Verhältnis von 1:1 erreicht, mit wachsender Entfernung wächst der Anteil hinter dem fokussierten Objekt kontinuierlich an, letzteres extrem, wenn die Unendlicheinstellung noch eben in den Schärfebereich gelegt wird (= hyperfokale Entfernung).
- Die Schärfentiefe ändert sich näherungsweise nicht, wenn ein Motiv einmal mit kurzer Brennweite aus geringer Entfernung und einmal mit langer Brennweite aus größerer Entfernung derart abgebildet wird, dass es im Bild die gleiche Größe hat. In diesem Fall ist der Abbildungsmaßstab konstant und somit auch die Schärfentiefe.
Diese Regel gilt, wenn in beiden Fällen die gleiche Blende verwendet wird und wenn der zweite Term im Nenner vernachlässigt werden kann: . Durch Substitution von ergibt sich als Bedingung für die Gültigkeit der Regel:
- .
Wie klein tatsächlich sein muss hängt vor allem vom akzeptablen Fehler und im geringen Maß von der Brennweite ab. Wird ein relativer Fehler von einem Prozent toleriert, darf die Differenz zwischen Gegenstandsweite und Brennweite 20 % der Hyperfokaldistanz nicht überschreiten.
- Durch das Verfahren des Focus stacking kann eine scheinbar extrem große Schärfentiefe erreicht werden, indem eine Bilderserie mit verschiedenen Entfernungseinstellungen aufgenommen wird und die Ergebnisse anschließend mit Methoden der Computergrafik neu zusammenmontiert werden.
- Umgekehrt lassen sich mittels der nach dem amerikanischen Fotografen Ryan Brenizer benannten Brenizermethode, der dieses Verfahren perfektioniert und bekannt gemacht hat, Weitwinkel- oder Panoramafotografien mit sehr geringer Schärfentiefe erzeugen. Hierbei werden mit einem lichtstarken Teleobjektiv angefertigte Aufnahmen mit kleinem Schärfebereich mittels Stitching zu einem Foto mit großem Bildwinkel kombiniert.
Kameraeinstellungen
Im Makrobereich kann die Schärfentiefe als Funktion des Abbildungsmaßstabs beschrieben werden (siehe oben).
Zur praktischen Anwendung im Feld ist der Verkleinerungsfaktor als Kehrwert des Abbildungsmaßstabs () oft geeigneter:
- man merke sich für seine aktuelle Kamera (den Wert für findet man in der Tabelle am Anfang dieses Artikels. Für Crop-DSLRs ergibt sich ein zu merkender Wert von ca. 0,4 mm; bei Vollformatkameras von ca. 0,6 mm)
- Für einen Verkleinerungsfaktor von 10, 5, 2, 1 muss man diesen Wert mit 110, 30, 6 bzw. 2 () multiplizieren und erhält 44 mm, 12 mm, 2,4 mm bzw. 0,8 mm für Crop-DSLRs bzw. 66 mm, 18 mm, 3,6 mm und 1,2 mm für Vollformatkameras.
- Das ergibt die Schärfentiefe für die Blendenzahl 10. Für andere Blendenzahlen erhöht bzw. verringert sich dieser Wert proportional.

Weitere Bemerkungen:
- Einige elektronisch gesteuerte Kameras bieten die Möglichkeit an, zuerst den vorderen und dann den hinteren Punkt des gewünschten Schärfebereiches mit dem Auslöser zu markieren (DEP-Funktion). Die Kamera berechnet dann die dafür benötigte Blende und stellt den Fokus so ein, dass die Schärfe genau dem markierten Bereich entspricht. Die A-DEP-Funktion aktueller Digitalkameras hat damit allerdings nichts zu tun, hier bestimmt die Kamera den vorderen und hinteren Schärfepunkt durch Nutzung aller AF-Felder.
- Die Verstellmöglichkeiten von Fachkameras erlauben das Nutzen der sogenannten Scheimpflug-Einstellung. Diese verändert nicht den Schärfenbereich des Objektivs, sondern erlaubt, die Schärfeebene zu verlagern und damit an das Motiv anzupassen. Für Klein- und Mittelformatkameras gibt es für den gleichen Einsatzzweck spezielle Tilt- bzw. Swing-Balgengeräte bzw. sogenannte Tilt-Objektive, eine Funktion, die oft auch mit einer Shift-Funktion zur möglichen Parallelverschiebung der Schärfenebene kombiniert wird.
- Einige Spezialobjektive verfügen über die Funktion der variablen Objektfeldwölbung (VFC, variable field curvature), die rotationssymmetrisch die stufenlose konvexe oder konkave Durchbiegung der Schärfenebene erlaubt.
- Mit einer speziellen Rechenscheibe lassen sich auch unterwegs für ein gegebenes Objektiv Schärfentiefe-Berechnungen durchführen. Bei gegebener Blende kann der optimale Fokuspunkt für einen gewünschten Schärfentiefe-Bereich oder der resultierende Schärfentiefe-Bereich bei gegebenem Fokuspunkt ermittelt werden. Außerdem lässt sich die zur Erreichung eines gewünschten Schärfentiefe-Bereiches nötige Blende bestimmen.
Anwendungen in der Computergrafik
Viele bekannte Verfahren in der Computergrafik nutzen aus Gründen der Geschwindigkeit direkte Transformationen (z. B. über Matrixmultiplikationen), um die Geometrie in Bilddaten zu überführen. Durch diese mathematischen Konstrukte ergibt sich jedoch auch eine unendliche Schärfentiefe. Da die Schärfentiefe jedoch auch als gestalterisches Mittel eingesetzt wird, wurden verschiedene Methoden entwickelt, um diesen Effekt nachzuahmen.
In 3D-Computerspielen hat sich das direkte Rendering von Polygonen durchgesetzt. Dieses Verfahren besitzt Geschwindigkeitsvorteile gegenüber dem indirekten Rendering (Raytracing), hat aber auch zugleich technische Einschränkungen. So lässt sich die Schärfentiefe nicht direkt berechnen, sondern muss in einem Postprocessing-Schritt mit Hilfe eines geeigneten Filters approximiert werden. Es handelt sich dabei um selektive Weichzeichner, die den Z-Buffer zur Kantenerkennung nutzen. Dadurch wird verhindert, dass beim Weichzeichnen des Bildes weiter vorn stehende Objekte in die Filterung des Hintergrunds mit einbezogen werden und umgekehrt. Probleme treten dabei insbesondere bei transparenten Objekten auf, da diese in separaten Postprocessing-Schritten behandelt werden müssen, was sich negativ auf die Geschwindigkeit des Bildaufbaus auswirkt.


Beim indirekten Rendering kann sowohl die zuvor beschriebene Methode als auch Multisampling verwendet werden, wobei zur Erzeugung eines Schärfentiefeeffekts sehr viele Samples nötig sind. Deshalb werden diese Verfahren vorzugsweise in Renderern eingesetzt, die unbiased sind. Diese entsprechen einem sehr nah an dem Modell einer Kamera angelehnten Verfahren, wo einzelne Photonen/Rays und deren Farbwert auf einem Film akkumuliert werden, d. h., mit fortlaufender Berechnung und höherer Samplezahl wird das Bildrauschen immer weiter reduziert. Im Gegensatz zu ersterem Verfahren erzeugt es glaubhaftere und realistischere Ergebnisse (Bokeh etc.), ist jedoch auch um Größenordnungen langsamer, weshalb es sich noch nicht für Echtzeitgrafik eignet.
Die Berechnung der Bilder in diesem Abschnitt erfolgte mit Hilfe eines Unbiased Renderers. Zur hinreichenden Rauschunterdrückung waren 2500 Abtastwerte pro Pixel notwendig, was einer Verfolgung von ca. 11,6 Milliarden Strahlengängen entspricht, die einschließlich multipler Spiegelungen und Brechungen in der Szene verfolgt wurden.
Siehe auch
- 35-Millimeter-Adapter (Schärfentiefe für herkömmliche Videokameras)
- Deep focus cinematography (möglichst große Schärfentiefe im Film)
- Beugungsunschärfe bei zu kleiner (geschlossener) Blende
Literatur
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. Verlag Harri Deutsch, Frankfurt/Main 1981, ISBN 3-87144-570-3, Kap. 6.4.3, S. 562–573.
- Andreas Feininger: Andreas Feiningers Große Fotolehre. Neuauflage. Heyne Verlag, München 2001, ISBN 3-453-17975-7.
- Michael J. Hussmann: Schärfentiefe – Theorie und Praxis. In: Fotomagazin. Februar 2020, S. 100–103.
Weblinks
- Schärfentiefe-Rechenscheibe download
- Schärfentiefe-Rechenscheibe Videoanleitung
- Schärfentiefe in der fotografischen Praxis
- Schärfentiefe, Berechnungsmethoden und -formeln im Wikibook Digitale bildgebende Verfahren
- Schärfentiefe-, Abbildungsmaßstab- und Nahlinsenrechner (deutsch). Berücksichtigt u. a. auch Beugung und Vorsatzlinsen. Kann individuelle Schärfentiefe-Tabellen ausgeben. Für Digitalkameras etwas komplizierter zu handhaben.
- Vergleich verschiedener Blendenzahlen und deren Schärfentiefe in Bildern
- Background blur calculator (englisch)
- dofmaster Berechnen der Schärfentiefe für unterschiedliche Kameras und Brennweiten in Abhängigkeit von der Blende (englisch). Kostenlose Software zur Erstellung von Schärfentiefe-Rechenscheiben.
Einzelnachweise
- Der Fotograf Emil Otto Hoppé gehörte zu den ersten, die das Manko sehr geringer Schärfentiefe als ästhetisches Stilmittel verwendete. In seinem Selbstporträt von 1926 (Bild unten (Memento des Originals vom 19. Juli 2011 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.) sind nur ein kleiner Teil seiner Hand sowie die Augen scharf – Hoppé liebte Hände.