Bändermodell
Das Bändermodell oder Energiebändermodell ist ein quantenmechanisches Modell zur Beschreibung von elektronischen Energiezuständen in einem idealen Einkristall. Dabei liegen die Atomrümpfe in einem streng periodischen Gitter vor. Es gibt mehrere Energiebereiche, in denen viele quantenphysikalisch mögliche Zustände existieren, die energetisch so dicht beieinander liegen, dass sie als Kontinuum – als Energieband – angesehen werden können. Die zugehörige Darstellung wird als Banddiagramm bezeichnet. Das Energiebändermodell eines Festkörpers ist dann die im Impulsraum dargestellte Bandstruktur (siehe unten bei E-k-Diagramm).
Entstehung der Bänder
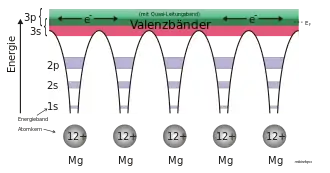
Betrachtet man ein einzelnes Atom, liegen die Energieniveaus der Elektronen im Feld des Atomkerns, in diskreter Form vor. Dies gilt auch für weit voneinander entfernte Atome. Nähert man zwei Atome einander an, so ist der beobachtete Effekt ähnlich wie bei gekoppelten Pendeln, bei denen sich die Anzahl der möglichen Schwingungsfrequenzen erhöht. Bei Atomen im Gitter und bei der Annäherung ab einem gewissen Abstand spalten sich die atomaren Elektronenniveaus aufgrund der elektrostatischen Wechselwirkung der Elektronen (dem entspricht die Koppelfeder der gekoppelten Pendel) der beiden Atome auf. Die Energieniveaus verschieben sich jeweils leicht nach oben und unten (siehe Zweizustandssystem). Betrachtet man nun einen Kristall, bei dem eine Vielzahl von Atomen miteinander wechselwirken, steigt die Anzahl der erlaubten Energiezustände entsprechend, sie verschmelzen zu gemeinsamen Energiebändern.
Dies ist die vereinfachte, anschaulichere Erläuterung. Physikalisch exakt entstehen die Bänder nicht durch elektrostatische Wechselwirkung der Elektronen, sondern durch die Bewegung der Elektronen im Feld der periodisch angeordneten Ionenrümpfe. Die Periodizität der Ionenrümpfe überträgt sich auf die Periodizität des resultierenden elektrostatischen Potentials, welches wiederum eine Periodizität der Wellenfunktion des Elektrons induziert. Es ist aber gerade die Eigenschaft der Periodizität der Wellenfunktion, welche zur Entstehung von quasi-kontinuierlichen, aber diskreten Energiespektren, d. h. Energiebändern führt. Das ist die Grundaussage des Bloch-Theorems.
Die Breite der Energiebänder ist für die unterschiedlichen atomaren Energieniveaus nicht gleich. Der Grund dafür ist die unterschiedlich starke Bindung der Elektronen an ihr Atom. Elektronen auf niedrigen Energieniveaus sind stärker gebunden und wechselwirken weniger mit Nachbaratomen. Dies führt zu schmalen Bändern. Die Valenzelektronen im Valenzband sind leichter gebunden und können daher die Potentialberge zwischen den Atomen einfacher überwinden. Sie wechselwirken stark mit denen der Nachbaratome und lassen sich in einem Kristall nicht mehr einem einzelnen Atom zuordnen, diese Bänder werden dabei breiter, siehe Abbildung.
Siehe auch: Modell der quasifreien Elektronen
Grundlagen für den Leitungsvorgang von elektrischen Ladungen

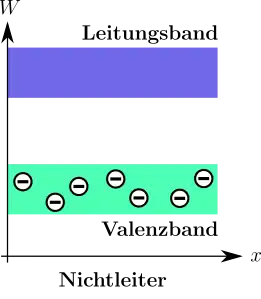
Bei der Betrachtung der elektrischen Eigenschaften eines Kristalls ist es von Bedeutung, ob die Energieniveaus in den äußeren, energetisch höchsten Energiebändern (dem Valenz- und dem Leitungsband) des Kristalls nicht besetzt, teilweise oder voll besetzt sind. Ein voll besetztes Band trägt, genau wie ein unbesetztes Band, nicht zum Ladungstransport bei. Die Ursache dafür ist, dass Elektronen in vollbesetzten Bändern keine Energie, z. B. durch ein elektrisches Feld, aufnehmen können, denn es gibt für sie keine unbesetzten Zustände mit etwas höherer Energie. Erst ein teilbesetztes Band ermöglicht im elektrischen Feld einen von Null verschiedenen Nettostrom. Dies ist aber nur eine notwendige Bedingung für den Stromfluss, wie sogenannte Mott-Isolatoren mit teilbesetzten Bändern aufzeigen, zu deren Erklärung elektronische Korrelationseffekte berücksichtigt werden müssen, die außerhalb der Gültigkeit des Bändermodells als „Ein-Elektronen-Dispersion“ des Festkörpers liegen.
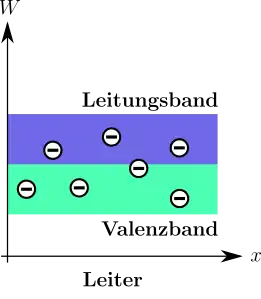
Die gute elektrische Leitfähigkeit von Metallen (auch bei tiefen Temperaturen) kommt durch das nur teilweise besetzte Leitungsband zustande (einwertige Metalle). Bei mehrwertigen Metallen kann es zwar vorkommen, dass das entsprechende Band theoretisch voll besetzt wäre, dieses Band überlappt jedoch bei Metallen mit dem nächsthöheren Band. In beiden Fällen sind nur teilweise besetzte Bänder vorhanden, so dass freie Energieniveaus für den Ladungstransport zur Verfügung stehen. Das Fermi-Niveau liegt in beiden Fällen im äußeren noch besetzten Band.
Auch bei Halbleitern und Isolatoren am absoluten Nullpunkt (Temperatur) ist das höchste Energieband vollständig mit Elektronen besetzt, dieses Band wird Valenzband genannt.[1][2] Im Gegensatz zu Metallen überlappt dieses Band nicht mit dem nächsthöheren Band, dem am absoluten Nullpunkt unbesetzten Leitungsband. Zwischen beiden Bändern liegt ein quantenmechanisch „verbotener Bereich“, der Bandlücke genannt wird. Da das Valenzband bei 0 K voll besetzt ist, kann kein Ladungstransport stattfinden. Führt man dem Material durch Temperaturerhöhung oder Lichteinstrahlung ausreichend Energie zu, können Elektronen die Bandlücke überwinden und ins Leitungsband angehoben werden. Auf diese Weise kann ein unbesetztes Leitungsband teilbesetzt werden. Diese Elektronen und die im Valenzband zurückbleibenden Löcher tragen beide zum elektrischen Strom bei (Eigenleitung).
Einteilung anhand der Lage der Bänder
Isolatoren und Halbleiter
Ein kristalliner Nichtleiter (auch als Isolator bezeichnet) hat ein nicht besetztes Leitungsband und eine so große Bandlücke (EG > 3 eV)[3], dass bei Raumtemperatur und auch bei deutlich höheren Temperaturen nur sehr wenige Elektronen vom Valenz- ins Leitungsband thermisch angeregt werden.[4] Der spezifische Widerstand eines solchen Kristalls ist sehr hoch. Durch Zufuhr von ausreichend viel Energie, also bei (sehr) hohen Temperaturen oder durch Anlegen einer genügend hohen Spannung, kann jedoch jeder Isolator zum Leiter werden, wobei dieser dann allerdings zerstört wird.[5]
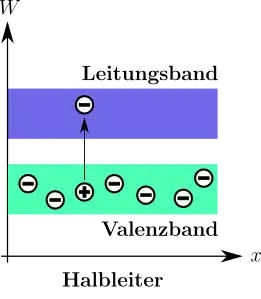
Ähnlich liegen die Verhältnisse bei einem kristallinen Halbleiter, jedoch ist die Bandlücke hier so klein (0,1 eV < EG < 3 eV[6]), dass sie durch thermische Energiezufuhr oder Absorption eines Photons (Photohalbleiter) gut überwunden werden kann. Ein Elektron kann ins Leitungsband angehoben werden und ist hier beweglich. Zugleich hinterlässt es im Valenzband eine Lücke, die durch benachbarte Elektronen aufgefüllt werden kann. Somit ist im Valenzband die Lücke beweglich. Man bezeichnet sie auch als Defektelektron, Elektronenfehlstelle oder Loch (siehe Löcherleitung). Bei Raumtemperatur weist ein Halbleiter dadurch eine geringe Eigenleitfähigkeit auf, die durch Temperaturerhöhung gesteigert werden kann.
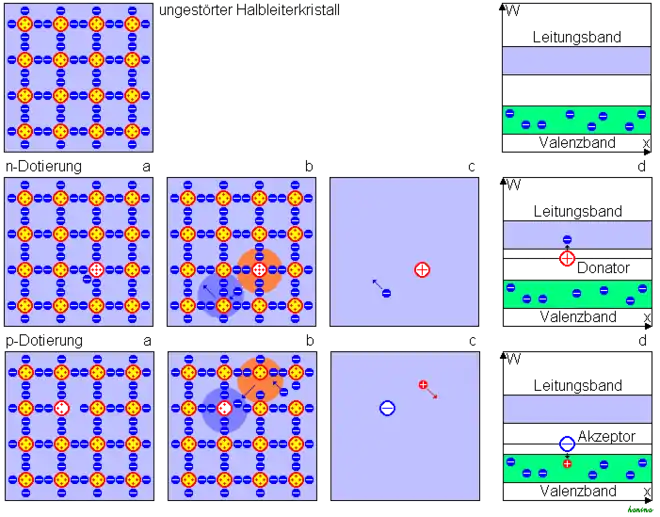
Durch Dotierung kann ein Halbleiter gezielt mit Ladungsträgern ausgestattet werden. Der Halbleiterkristall beruht auf einem Kristallgitter aus 4-wertigen Atomen, die jeweils durch vier Elektronenpaare gebunden sind. Dotierung mit 5-wertigen Atomen hinterlässt im Gitter ein für die Bindung nicht erforderliches Elektron, das somit nur locker gebunden ist (Abbildung unten, Bild a). Mit nur geringer Energie kann es daher ins Leitungsband angehoben werden und ist hier beweglich (Bild b). Ein solches Atom nennt man einen Elektronen-Donator (lateinisch donare ‚geben‘). Der Kristall wird mit beweglichen negativen Ladungsträgern ausgestattet, man spricht von einer n-Dotierung. Zugleich bleibt ein positiver Atomrumpf im Gitter zurück. Lässt man den Hintergrund der neutralen Grundsubstanz außer Betracht (Bild c), so hat man eine positive feste und eine negative bewegliche Ladung ins Gitter eingebracht. Energetisch liegt ein Donator knapp unterhalb des Leitungsbandes, da wegen der schwachen Bindung des „zusätzlichen“ Elektrons wenig Energie zur Anregung ins Leitungsband vonnöten ist (Bild d).
Dotierung mit 3-wertigen Atomen führt zu einer ungesättigten Bindung, in der ein Elektron fehlt. Dieses kann mit geringem Energieaufwand aus einer anderen Bindung gerissen werden. Ein solches Atom nennt man einen Elektronen-Akzeptor (lat. accipere ‚annehmen‘), das energetisch knapp oberhalb des Valenzbandes liegt. Es entsteht eine negative ortsfeste Ladung. Zugleich hinterlässt das Elektron im Kristall eine Lücke, die durch ein anderes Elektron aufgefüllt werden kann, also eine bewegliche Elektronenfehlstelle. Im Resultat hat man eine negative feste und eine positive bewegliche Ladung eingebracht. Man spricht dann von p-Dotierung.
Eine wichtige Anwendung finden die dotierten Kristalle in der Mikroelektronik, deren Strukturen vor allem auf Halbleiterdioden beruhen. Diese werden aus einem p-n-Übergang gebildet, das heißt aus einer Kombination eines p-dotierten mit einem n-dotierten Kristall.
Es gibt jedoch auch Halbleiter (und Isolatoren), auf die das Bändermodell nicht anwendbar ist. Dazu gehören beispielsweise sogenannte Hopping-Halbleiter,[7] bei ihnen ist der dominierende Mechanismus für den Ladungsträgertransport das Hopping (englisch für ‚hüpfen‘). Die Elektronen „wandern“ daher nicht durch das Leitungsband von einem Ort zum anderen, sondern „springen“ sozusagen von Atom zu Atom.
Metalle und Halbmetalle
In einem Metall spricht man meist nicht von Leitungs- bzw. Valenzband. Dennoch gilt auch hier, das höchste vollständig besetzte Band ist das Valenzband. Das darüberliegende teilweise besetzte Band kann als Leitungsband bezeichnet werden.[1][2]
Bei einwertigen Metallen ist das höchste besetzte Energieband zur Hälfte aufgefüllt. Bei mehrwertigen Metallen überlappen sich die äußeren Energiebänder teilweise. Elektronen können daher beim Anlegen von beliebig kleinen elektrischen Feldstärken in einen höheren Energiezustand wechseln (sich sozusagen frei bewegen) und zum elektrischen Stromfluss beitragen, deswegen sind Metalle gute elektrische Leiter. Eine Temperaturerhöhung führt im Allgemeinen zur Verringerung der Leitfähigkeit des Kristalls, da die erhöhte Streuung der Elektronen eine niedrigere mittlere Geschwindigkeit bedingt. Das Ferminiveau liegt bei Metallen bzw. Halbmetallen innerhalb des höchsten besetzten Bandes bzw. im Überlappungsbereich der Bänder.
Bei Halbmetallen liegt die Unterkante des Leitungsbands nur wenig tiefer als die Oberkante des Valenzbandes. Diese geringe Überlappung führt bereits bei Temperaturen um den absoluten Nullpunkt zu einer geringen Konzentration von Elektronen im Leitungsband und Löchern im Valenzband.
E-k-Diagramm
In den Abbildungen oben sind die Energieniveaus eindimensional über der Ortskoordinate aufgetragen. Für die Betrachtung der Vorgänge beim Sprung eines Elektrons von einem Band zum anderen hat sich dagegen die Darstellung über dem Wellenvektor bewährt. Dies wird unter dem Stichwort Bandstruktur genauer erläutert.
Geschichte
Das Bändermodell der Elektronenleitung in Metallen wurde 1928 von Felix Bloch[8] entwickelt (in seiner Dissertation bei Werner Heisenberg in Leipzig), damals noch als Einelektronenmodell in periodischem Potential, er betrachtete nur das Grundzustands-Band und keine Wechselwirkung der Elektronen untereinander. Unabhängig und gleichzeitig geschah das 1928 durch Hans Bethe in seiner Münchner Dissertation bei Arnold Sommerfeld. In den darauffolgenden Jahren wurde es von Rudolf Peierls (ab 1929 bei Heisenberg in Leipzig), Léon Brillouin und Alan Herries Wilson (1931) weiterentwickelt. Wilson betrachtete auch Isolatoren und Halbleiter anhand der Bandstruktur. Realistische Bandstruktur-Berechnungen setzten mit einer Arbeit von Eugene Wigner und Frederick Seitz über das Natrium-Gitter 1933 ein, in der auch die Wigner-Seitz-Zelle eingeführt wurde. Zu den frühen Forschern auf diesem Gebiet zählten John C. Slater am MIT und Nevill Mott und Harry Jones in Bristol.[9]
Weblinks
- Was ist das Bändermodell? (Memento vom 1. Mai 2010 im Internet Archive)
Einzelnachweise
- Hans-Jürgen Bargel, Hermann Hilbrans (Hrsg.): Werkstoffkunde. 10., bearbeitete Auflage. Springer, Berlin u. a. 2008, ISBN 978-3-540-79296-3, S. 11 (eingeschränkte Vorschau in der Google-Buchsuche).
- Wolfgang Demtröder: Atome, Moleküle und Festkörper (= Experimentalphysik. Band 3). 3., überarbeitete Auflage. Springer, Berlin u. a. 2005, ISBN 3-540-21473-9, S. 441 (eingeschränkte Vorschau in der Google-Buchsuche).
- Rudolf Gross, Achim Marx: Festkörperphysik. Walter de Gruyter GmbH & Co KG, 2014, ISBN 978-3-11-035870-4 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 23. Dezember 2016]).
- Heinrich Frohne, Karl-Heinz Löcherer, Hans Müller, Franz Moeller: Moeller Grundlagen der Elektrotechnik. Springer-Verlag, 2005, ISBN 978-3-519-66400-0 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 23. Dezember 2016]).
- Hansgeorg Hofmann, Jürgen Spindler: Werkstoffe in der Elektrotechnik: Grundlagen – Struktur – Eigenschaften – Prüfung – Anwendung – Technologie. Carl Hanser Verlag GmbH & Company KG, 2013, ISBN 978-3-446-43748-7 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 23. Dezember 2016]).
- A. F. Holleman, E. Wiberg, N. Wiberg: Lehrbuch der Anorganischen Chemie. 101. Auflage. Walter de Gruyter, Berlin 1995, ISBN 3-11-012641-9, S. 1313.
- Erwin Riedel, Christoph Janiak: Anorganische Chemie. 7. Auflage. Walter de Gruyter, Berlin u. a. 2007, ISBN 978-3-11-018903-2, S. 724 ff.
- Felix Bloch: Über die Quantenmechanik der Elektronen in Kristallgittern. In: Zeitschrift für Physik. Band 52, Nr. 7–8, 1. Juli 1929, S. 555–600, doi:10.1007/BF01339455.
- Zur Geschichte: Lillian Hoddeson u. a. (Hrsg.): Out of the Crystal Maze. Chapters in the history of solid state physics. Oxford University Press 1992, Kapitel 2: Lillian Hoddeson, Gordon Baym, Michael Eckert: The development of the quantum mechanical electron theory of metals 1926–1933. S. 88–181, Kapitel 3: Paul Hoch: The development of the band theory of solids 1933–1960. S. 182–235.
Siehe auch: Lillian Hoddeson, Gordon Baym, Michael Eckert: The development of the quantum-mechanical electron theory of metals: 1928–1933. In: Reviews of Modern Physics. Band 59, Nr. 1, 1987, S. 287–327, doi:10.1103/RevModPhys.59.287.