Valenzband
Der Begriff Valenzband gehört zum Bändermodell, mit dem die elektrische Leitfähigkeit, speziell die der Halbleiter, erklärt wird. Das Valenzband ist im Allgemeinen das höchste besetzte Elektronenenergieband am absoluten Nullpunkt (Temperatur) bzw. es sind die Bänder, deren Elektronen (Valenzelektronen) zur chemischen Bindung beitragen.
.svg.png.webp)
Erklärungen
Wie oben erwähnt ist das Valenzband das höchste besetzte Energieband am absoluten Nullpunkt (Temperatur). Bei Halbleitern und Isolatoren ist dieses Band vollständig besetzt und durch die so genannte Bandlücke vom nächsthöheren Energieband (Leitungsband) getrennt. Bei Leitern kann – je nach Elektronenkonfiguration des Elements – das Valenzband entweder identisch mit dem Leitungsband sein (z. B. bei Natrium), oder es kann sich mit dem nächsthöheren Band (quasi das Leitungsband) überlagern. Daraus resultiert, dass das Valenzband bei Metallen nur teilweise besetzt ist.
Für den Fall eines einwertigen Metalls trägt jedes Atom im Kristallverbund ein Valenzelektron zur Bindung bei (Grundkonfiguration 3s1). Die Valenzelektronen gehören, als Ursache der chemischen Bindung, dem Festkörper als Ganzem an. So entsteht im Fall von Natrium (einwertiges Metall) das 3s-Band, dem Valenzband von Natrium; zur Entstehung der Bänder siehe Bändermodell. Da Natrium nur ein Valenzelektron für das entsprechende Energieniveau und somit auch zum entsprechenden Energieband beiträgt, ist das 3s-Band nur zur Hälfte besetzt (vgl. Pauli-Prinzip).
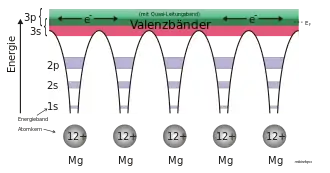
Anders sieht dies bei zweiwertigen Metallen wie Magnesium aus. Magnesium besitzt zwei Valenzelektronen (Grundkonfiguration 3s2), es wäre demnach zu erwarten, dass sein Valenzband voll besetzt und daher ein Isolator ist. Durch die energetische Überlagerung mit dem nächsthöheren Energieband (auch II. Valenzband genannt, im Fall von Magnesium das 3p-Band) können Elektronen vom I. in das II. Valenzband übertreten, so dass beide nur teilbesetzt sind; dabei sind die Elektronen nicht einfach anteilsmäßig, sondern in Abhängigkeit von den Zustandsdichten verteilt (vgl. auch Bandstruktur). Analog verhält es sich im Fall von Aluminium (Grundkonfiguration 3s2 3p1), bei dem das 3-s-Band vollbesetzt und das 3-p-Band halbbesetzt sein müsste. Durch die Überlagerung der Energiebänder sind aber wie beim Magnesium beide Bänder nur teilweise besetzt.
Bei Halbleitern und Isolatoren existiert die beschriebene Überlagerung des Valenzbandes und des nächsthöheren (unbesetzten) Bandes nicht. Beispielsweise besitzt Silizium vier Valenzelektronen (Grundkonfiguration 3s2 3p2). Ähnlich wie bei Natrium, Magnesium und Aluminium überlagern sich auch hier die beiden Valenzbänder (3s- und 3p-Band). Da aber keine Überlagerung mit dem nächsthöheren Band vorliegt – zur Veranschaulichung kann auch das Energieschema von Kohlenstoff[1] genutzt werden – ist das Valenzband (hier werden häufig beide Valenzbänder einfach zusammengefasst) vollständig besetzt. Die energetische Lücke zwischen dem Valenzband und dem Leitungsband bezeichnet man als Bandlücke, einer quantenmechanisch verbotenen Zone für Elektronen. Da keine freien Energieniveaus im Valenzband existieren, ist Silizium beim absoluten Nullpunkt (T = 0 K) ein Isolator, denn ein äußeres (kleines) elektrisches Feld kann keine Valenzelektronen in das freie Leitungsband befördern. Da es mit steigender Temperatur oder Lichteinfall möglich ist, dass Elektronen in das Leitungsband wechseln können, bezeichnet man Silizium auch als Halbleiter.
Bedeutung bei der elektrischen Leitung
Grundzustand und äußeres elektrisches Feld
Voll besetzte Bänder können zur Leitfähigkeit nicht beitragen, denn beim Anlegen eines äußeren elektrischen Feldes nehmen Elektronen Energie aus diesem Feld auf, sie werden auf freie höhere Energieterme im Band gehoben und es kommt zu Bandverbiegungen. Damit sich Elektronen im Festkörper bewegen können, sind freie Energiezustände notwendig. Bei einem vollbesetzten Band können die Elektronen durch die zugeführte Energie des elektrischen Feldes kein höheres Energieniveau im selben Band annehmen. Da auch eine Ortsveränderung der gesamten Elektronen keinen Nettotransport von elektrischer Ladung mit sich bringt, ist ein Material mit vollbesetztem Valenzband ein Isolator.
Externe Energiezufuhr
Wird jedoch einem Halbleiter eine thermische oder photonische Energiemenge zugeführt, die im Bereich der Bandlücke liegt, so werden viele Valenzelektronen in das Leitungsband angeregt. Diese Elektronen im Leitungsband können Energie von einem elektrischen Feld aufnehmen und machen das Material (zusammen mit den entstandenen Defektelektronen, d. h. „Löchern“ im Valenzband) leitfähig. Diesen stark mit der Temperatur zunehmenden Effekt bezeichnet man als Eigenleitung, im Fall der Anregung durch Photonen als Photoleitung. Im Gegensatz dazu steht die Störstellenleitung, die durch das Einbringen von Fremdatomen (Dotierung) in den Halbleiter erzeugt werden kann.
Halbleiter und Isolatoren unterscheiden sich nur durch die Breite der Bandlücke. Bei letzteren ist diese so groß (Eg > 3 eV), dass Elektronen sie bei Zimmertemperatur und auch bei höheren Temperaturen kaum durch thermische Anregung überwinden können.[2] Erst bei (sehr) hohen Temperaturen oder durch das Anlegen einer genügend hohen Spannung verwandeln sich Isolatoren in Leiter, wobei diese dabei allerdings meist irreversibel zerstört werden.[3][4][5]
Einzelnachweise
- Energieschema von Kohlenstoff
- Peter W. Atkins, Julio De Paula: Physikalische Chemie. John Wiley & Sons, 2013, ISBN 978-3-527-33247-2, S. 764,765 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 1. Februar 2017]).
- Hansgeorg Hofmann, Jürgen Spindler: Werkstoffe in der Elektrotechnik: Grundlagen - Struktur - Eigenschaften - Prüfung - Anwendung - Technologie. Carl Hanser Verlag GmbH & Company KG, 2013, ISBN 978-3-446-43748-7, S. 105 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 1. Februar 2017]).
- Matthias Günther: Energieeffizienz durch Erneuerbare Energien: Möglichkeiten, Potenziale, Systeme. Springer-Verlag, 2014, ISBN 978-3-658-06753-3, S. 70 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 1. Februar 2017]).
- Wilfried Plaßmann, Detlef Schulz: Handbuch Elektrotechnik: Grundlagen und Anwendungen für Elektrotechniker. Springer-Verlag, 2013, ISBN 978-3-8348-2071-6, S. 202 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 1. Februar 2017]).