Eigenleitung

Eigenleitung (auch intrinsische Leitung) bezeichnet in der Festkörperphysik die relativ geringe elektrische Leitfähigkeit undotierter (reiner) Halbleiter. Materialien, bei denen die Eigenleitung der bestimmende Mechanismus für die Leitfähigkeit von elektrischem Strom ist, nennt man Eigenhalbleiter (oder intrinsischer Halbleiter). Im Gegensatz dazu führen die Störstellen in dotierten Halbleitern (Störstellenleitern) zu einer Erhöhung der elektrischen Leitfähigkeit, hier dominiert die Störstellenleitung.

Wesentlich früher als in Halbleitern ist die Eigenleitfähigkeit in Flüssigkeiten untersucht worden, beispielsweise in[1]. Diese müssen, wenn sie elektrisch neutral sind, zu einem gewissen Anteil dissoziiert sein, um elektrisch leiten zu können.

Beschreibung

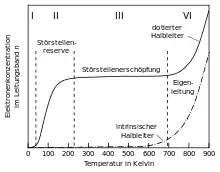
Leitungsmechanismen im dotierten und undotiertem Halbleiter in Abhängigkeit von der Temperatur

Die elektrische Leitfähigkeit fester Materialien ist hauptsächlich durch die Verfügbarkeit von Ladungsträgern und freien Energieniveaus in den Energiebändern bestimmt, d. h. leere sowie volle Energiebänder ermöglichen keinen Ladungstransport.

Am absoluten Nullpunkt (bei 0 K) steht nicht ausreichend Energie zur Verfügung, um Elektronen in das Leitungsband oder auf Störstellenniveaus anzuregen, daher unterscheiden sich dotierte und undotierte Halbleiter hier hinsichtlich der Ladungsträgerdichte nicht.

Mit zunehmender Temperatur steigt die zur Verfügung stehende Energie (z. B. der Phononen), so dass sich auch die Wahrscheinlichkeit der thermischen Anregung eines Elektrons vom Valenzband in das Leitungsband erhöht. Die Bandabstandsenergie liegt bei typischen Halbleitern wie Germanium oder Silizium im Bereich von 0,5 bis 3,5 eV und somit meist deutlich höher als der Abstand von Valenz- oder Leitungsband zu den Störstellenniveaus (0,01 bis 0,5 eV[2]) in dotierten Halbleitern. Somit steigt die elektrische Leitfähigkeit durch Eigenleitung erst bei deutlich höheren Temperaturen als bei Störstellenleitung.

Eigenleitfähigkeit

Für die elektrische Leitfähigkeit eines Halbleiters lässt sich kaum eine charakterisierende Materialkonstante angeben, da die Leitfähigkeit um mehrere Größenordnungen durch Verunreinigung oder Dotierung des Halbleiters veränderbar ist. Bei Silizium sind Werte im Bereich 10⁰…10⁶ S/m möglich.[3] Für Germanium mit einem Reinheitsgrad > 99,999 % wird der spezifische Widerstand bei 20 °C mit 53000 μΩ·cm angegeben;[4] das entspricht einem Leitwert von 1.9e³ S/m. Dieser Wert liegt um drei Größenordnungen über dem Wert der nachfolgend berechneten intrinsischen oder Eigenleitfähigkeit. Entsprechendes wird für Silizium berichtet.[5] Eine repräsentative Konstante des Halbleiters lässt sich nur für einen Zustand angeben, der vom Reinheitsgrad unabhängig ist, das ist der Zustand der Eigenleitung.

Daten zur Eigenleitfähigkeit bei 300 K
Material	$n_{\mathrm {i} }$ in ${\tfrac {1}{{\text{cm}}^{3}}}$	$b_{\mathrm {n} }$ in $\mathrm {\tfrac {cm^{2}}{Vs}}$	$b_{\mathrm {p} }$ in $\mathrm {\tfrac {cm^{2}}{Vs}}$	$\sigma _{\mathrm {i} }$ in $\mathrm {\tfrac {S}{m}}$	Quelle
Germanium	2.4e¹³	3600	1700	2,0	[6]
	2.4e¹³	3900	1900	2,2	[7]
	2.3e¹³	3900	1900	2,1	[8]
Silizium	6.8e¹⁰	1400	400	2.0e^-3	[6]
	1.5e¹⁰	1350	850	0.5e^-3	[7]
	1.5e¹⁰	1350	480	0.4e^-3	[8]

Zur Leitfähigkeit $\sigma$ tragen nicht nur die freien Elektronen bei, sondern auch die zurückbleibenden Defektelektronen (Löcher), jeweils mit ihren negativen oder positiven Ladungen, ihren Beweglichkeiten $b_{\mathrm {n} }$ , $b_{\mathrm {p} }$ und ihren Teilchendichten $n_{\mathrm {n} }$ , $n_{\mathrm {p} }$ .

Mit der Elementarladung $e$ ergibt sich[9]

\sigma =e\,(n_{\mathrm {n} }\,b_{\mathrm {n} }+n_{\mathrm {p} }\,b_{\mathrm {p} })

.

Bei der Eigenleitung sind die Teilchendichten gleich groß und gleich der Eigenleitungsdichte $n_{\mathrm {i} }=n_{\mathrm {p} }=n_{\mathrm {n} }$ . Damit ergibt sich die Eigenleitfähigkeit zu

\sigma _{\mathrm {i} }=e\,n_{\mathrm {i} }\,(b_{\mathrm {n} }+b_{\mathrm {p} })

.

Die erforderlichen Daten und die Ergebnisse stehen in der beigefügten Tabelle. Die unterschiedlichen Angaben in verschiedenen Quellen zeigen die Schwierigkeit auf, um selbst für die Eigenleitung zu verlässlichen Daten zu kommen.

Die Eigenleitungsdichte sollte im Verhältnis zur Atomdichte $n_{\mathrm {A} }=4\ldots 5\cdot 10^{22}\,\mathrm {cm} ^{-3}$ gesehenen werden.[6][8] Mit den Tabellenwerten für 300 K ist

n_{\mathrm {i} }/n_{\mathrm {A} }<10^{-9}

für Germanium und

<10^{-12}

für Silizium.

Das bedeutet, dass für den eigenleitenden Zustand auf 10⁹ Germaniumatome höchstens ein Fremdatom kommen darf.[10]

Die niedrigste Verunreinigungskonzentration, die sich bei Halbleitereinkristallen heute erreichen lässt, liegt bei 10¹² cm⁻³.[11] Damit ist bei Zimmertemperatur eigenleitendes Germanium möglich. Bei Silizium und bei technisch verwendetem Germanium mit einer Störstellenkonzentration 10¹⁵…10¹⁸ cm⁻³ [12] ist bei Zimmertemperatur Eigenleitung nicht möglich.

Eigenleitfähigkeit in Flüssigkeiten

Im Gegensatz zu den Halbleitern gibt es hier die elektrolytische Leitfähigkeit, die mit dem Transport von Materie in Form von positiven und negativen Ionen verbunden ist. Beispielsweise im Leitungswasser sind diese durch gelöste Salze reichlich vorhanden, und ihre Konzentrationen (und Beweglichkeiten) bestimmen die Leitfähigkeit. Bei Reinstwasser geht damit die Leitfähigkeit wegen fehlender Salze nicht gegen null, sondern es gibt eine Eigenleitfähigkeit, die gegenüber der Leitfähigkeit durch Fremdionen überwiegen kann, denn Wasser selbst dissoziiert zu einem geringen Anteil[13] in protonierte Wassermoleküle (H₃O⁺) und Hydroxidionen (HO⁻). Die Eigenleitfähigkeit von Wasser liegt bei 4,2 μS/m bei 20 °C und 5,5 μS/m bei 25 °C. Diese wird aber nicht mehr (wie früher mit hohem Reinigungsaufwand) gemessen, sondern berechnet.[13] Bei Verunreinigungen des Wassers im Spurenbereich lassen sich in ihre Beiträge zur Leitfähigkeit von der Eigenleitfähigkeit des Wassers nicht unterscheiden.

Bei organischen Substanzen ist die Leitfähigkeit im Allgemeinen sehr gering. Anders als bei Wasser ist ein natürliches Minimum der Leitfähigkeit nicht bekannt, so dass sie vom Reinheitsgrad abhängig bleibt, und diese Leitfähigkeit wird dann als Eigenleitfähigkeit bezeichnet.[14][15] Die organische Substanz muss nur über ein Ionisierungsvermögen für einen Elektrolyten verfügen,[14] wenn sich die Leitfähigkeit des Fremdstoffes von der Eigenleitfähigkeit abheben soll.

Siehe auch

Intrinsische Leitfähigkeit

Einzelnachweise

Jahresbericht über die Fortschritte der Chemie und verwandter Theile anderer Wissenschaften. Vieweg, 1904, S. 156.
S. M. Sze: Physics of Semiconductor Devices. 2. Auflage. Wiley & Sons, 1981, ISBN 0-471-09837-X, S. 21 (Neuere Auflagen enthalten keine Übersicht für Germanium).
Konrad Reif (Hrsg.): Bosch Autoelektrik und Autoelektronik: Bordnetze, Sensoren und elektronische Systeme. 6. Aufl., Vieweg + Teubner, 2011, ISBN 9783834899026, S. 168.
Prospektblatt Ge 99,999 % siehe Eigenschaften; abgerufen 10. November 2019.
Henricus P. J. Wijn, Peter Dullenkopf: Werkstoffe der Elektrotechnik: Physikalische Grundlagen der technischen Anwendungen. Springer, 1967, ISBN 978-3-642-88698-0, S. 59.
Franz Moeller (Begr.), Hans Fricke, Heinrich Frohne, Paul Vaske: Grundlagen der Elektrotechnik. 17. Aufl., Springer, 1986, ISBN 3663121569, S. 234.
Wilfried Plaßmann, Detlef Schulz (Hrsg.): Handbuch Elektrotechnik: Grundlagen und Anwendungen für Elektrotechniker. 5. Aufl., Vieweg+Teubner, 2009, ISBN 978-3-8348-0470-9, S. 231.
Leonhard Stiny: Aktive elektronische Bauelemente: Aufbau, Struktur, Wirkungsweise, Eigenschaften und praktischer Einsatz. 4. Aufl., Springer-Vieweg, 2019, ISBN 978-3-658-24751-5, S. 28.
Wilfried Plaßmann, Detlef Schulz (Hrsg.): Handbuch Elektrotechnik: Grundlagen und Anwendungen für Elektrotechniker. 5. Aufl., Vieweg+Teubner, 2009, ISBN 978-3-8348-0470-9, S. 225.
Eberhard Spenke: Elektronische Halbleiter: Eine Einführung in die Physik der Gleichrichter und Transistoren. Springer, 1955, S. 26 f, Fußnote 2.
Harald Ibach, Hans Lüth: Festkörperphysik: Einführung in die Grundlagen. 7. Aufl., Springer, 2009, ISBN 9783540857952, S. 416.
Reinhold Paul: Transistoren: Physikalische Grundlagen und Eigenschaften. Springer und Vieweg, 1965, S. 24 f.
Kurt Marquardt et al: Rein- und Reinstwasseraufbereitung. Expert-Verlag, 1994, S. 273 ff.
Hugo Josef Kauffmann: Beziehungen zwischen physikalischen Eigenschaften und chemischer Konstitution. Enke, 1920, S. 364 ff.
Robert Kremann, Robert Müller: Elektromotorische Kräfte, Elektrolyse und Polarisation. Akad. Verlagsgesellschaft, 1924, S. 285.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Jahresbericht über die Fortschritte der Chemie und verwandter Theile anderer Wissenschaften. Vieweg, 1904, S. 156.

[Sze1981-2] S. M. Sze: Physics of Semiconductor Devices. 2. Auflage. Wiley & Sons, 1981, ISBN 0-471-09837-X, S. 21 (Neuere Auflagen enthalten keine Übersicht für Germanium).

[3] Konrad Reif (Hrsg.): Bosch Autoelektrik und Autoelektronik: Bordnetze, Sensoren und elektronische Systeme. 6. Aufl., Vieweg + Teubner, 2011, ISBN 9783834899026, S. 168.

[4] Prospektblatt Ge 99,999 % siehe Eigenschaften; abgerufen 10. November 2019.

[5] Henricus P. J. Wijn, Peter Dullenkopf: Werkstoffe der Elektrotechnik: Physikalische Grundlagen der technischen Anwendungen. Springer, 1967, ISBN 978-3-642-88698-0, S. 59.

[Moeller-6] Franz Moeller (Begr.), Hans Fricke, Heinrich Frohne, Paul Vaske: Grundlagen der Elektrotechnik. 17. Aufl., Springer, 1986, ISBN 3663121569, S. 234.

[PlaSch-7] Wilfried Plaßmann, Detlef Schulz (Hrsg.): Handbuch Elektrotechnik: Grundlagen und Anwendungen für Elektrotechniker. 5. Aufl., Vieweg+Teubner, 2009, ISBN 978-3-8348-0470-9, S. 231.

[Stiny-8] Leonhard Stiny: Aktive elektronische Bauelemente: Aufbau, Struktur, Wirkungsweise, Eigenschaften und praktischer Einsatz. 4. Aufl., Springer-Vieweg, 2019, ISBN 978-3-658-24751-5, S. 28.

[9] Wilfried Plaßmann, Detlef Schulz (Hrsg.): Handbuch Elektrotechnik: Grundlagen und Anwendungen für Elektrotechniker. 5. Aufl., Vieweg+Teubner, 2009, ISBN 978-3-8348-0470-9, S. 225.

[10] Eberhard Spenke: Elektronische Halbleiter: Eine Einführung in die Physik der Gleichrichter und Transistoren. Springer, 1955, S. 26 f, Fußnote 2.

[11] Harald Ibach, Hans Lüth: Festkörperphysik: Einführung in die Grundlagen. 7. Aufl., Springer, 2009, ISBN 9783540857952, S. 416.

[12] Reinhold Paul: Transistoren: Physikalische Grundlagen und Eigenschaften. Springer und Vieweg, 1965, S. 24 f.

[Marquardt-13] Kurt Marquardt et al: Rein- und Reinstwasseraufbereitung. Expert-Verlag, 1994, S. 273 ff.

[Kauffmann-14] Hugo Josef Kauffmann: Beziehungen zwischen physikalischen Eigenschaften und chemischer Konstitution. Enke, 1920, S. 364 ff.

[15] Robert Kremann, Robert Müller: Elektromotorische Kräfte, Elektrolyse und Polarisation. Akad. Verlagsgesellschaft, 1924, S. 285.