p-n-Übergang

Ein p-n-Übergang bezeichnet einen Materialübergang in Halbleiterkristallen zwischen Bereichen mit entgegengesetzter Dotierung. Bereiche, in denen die Dotierung von negativ (n) zu positiv (p) wechselt, kommen in vielen elektrischen Bauelementen der Halbleitertechnik vor. Die Besonderheit des p-n-Übergangs ist die Ausbildung einer Raumladungszone (auch Verarmungszone oder Sperrschicht genannt), die beim Anlegen einer äußeren Spannung Stromfluss nur in einer Richtung zulässt.[1][2][3] So wirkt ein p-n-Übergang wie ein „Stromventil“, welches beispielsweise bei Einkristall-Halbleiterdioden eingesetzt wird und angelegten Strom sperrt (Sperrzustand) oder durchlässt (Durchlasszustand).

p-n-Übergang im Gleichgewicht

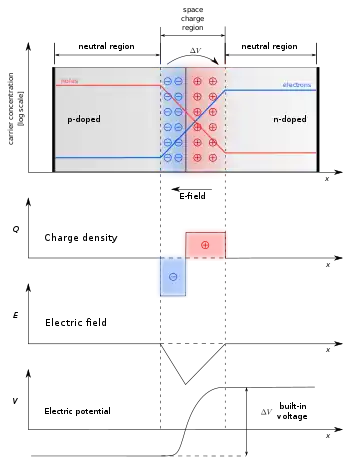
Aufbau einer Sperrschicht (Raumladungszone, RLZ) im asymmetrischen p-n-Übergang (p-Seite ist hier stärker dotiert). Ausgehend von der Ladungsverteilung im obersten Bild erhält man das elektrische Feld sowie das elektrische Potential am Übergang durch Integrieren der Poissongleichung. Aufgrund des gaußschen Integralsatzes und der ersten Maxwellgleichung muss das elektrische Feld außerhalb der Raumladungszone null sein, da die Gesamtladung der gesamten Raumladungszone die elektrische Neutralität nicht verletzen darf.

Wie intrinsische Halbleiter sind auch dotierte Halbleiter in ihrem Grundzustand (am absoluten Nullpunkt) ungeladen. Elektronen und Löcher sind hier an ihre Dotieratome fest gebunden (örtlich lokalisiert) und stehen nicht für den Ladungstransport zur Verfügung. Die in dotierten Halbleitern auftretenden Donator- und Akzeptorzustände liegen jedoch in der Regel sehr nahe am Leitungs- bzw. Valenzband, so dass Elektronen schon bei geringen Temperaturen aus bzw. in diese Energieniveaus angeregt werden (vgl. Störstellenleitung). Die frei beweglichen Elektronen bzw. Löcher stellen ein Elektronen- bzw. Löchergas dar, das für den Ladungstransport bereitsteht. Trotz diesen frei beweglichen Ladungsträgern ist ein solcher (nicht verbundener) dotierter Halbleiter weiterhin insgesamt elektrisch neutral. Diese nach außen wirkende Ladungsneutralität gilt auch für zwei entgegengesetzt dotierte Halbleiterstücke bzw. -bereiche, einem pn-Übergang. Im Inneren sind die Verhältnisse jedoch komplizierter und bestimmen das elektrische Verhalten bei äußerlich angelegtem elektrischen Potential.

Betrachtet man einen abrupten pn-Übergang, das heißt die Verbindung zweier gleichförmig dotierter n- und p-Bereiche, entsteht aufgrund des Konzentrationsgradienten der frei beweglichen Ladungsträger zwischen den beiden Bereichen eine gerichtete thermische Bewegung hin zur kleineren Konzentration (Diffusion). Die Majoritätsladungsträger wandern in den jeweils anderen Bereich, in denen ihre Konzentration geringer ist (Konzentrationsdiffusion). Das heißt: Die Elektronen des n-Kristalls streben in den p-Kristall und rekombinieren dort mit Löchern. Löcher des p-Kristalls diffundieren auf die n-Seite und rekombinieren dort mit freien Elektronen. Durch diese Ladungsträgerbewegung und -rekombination fehlen nun auf beiden Seiten Ladungsträger, die Bereiche „verarmen“ an Ladungsträgern. Die zu den nun fehlenden beweglichen Ladungsträgern gehörenden ortsfesten Dotierungsatome mit ihren jetzt nicht mehr elektrisch kompensierten Raumladungen verursachen ein elektrisches Feld zwischen den beiden Bereichen, welches eine Kraft auf die verbleibenden freien Ladungsträger ausübt. Die dadurch verursachte Driftbewegung ist der durch Diffusion verursachten Bewegung entgegen gerichtet und es stellt sich ein Gleichgewicht zwischen beiden ein.

Beiderseits der Grenze zwischen p- und n-Kristall entsteht eine Zone ohne freie Ladungsträger (Verarmungszone), in der nur noch die ortsfesten Raumladungen der Dotierungsatome verbleiben (Raumladungszone, RLZ). Die Ausdehnung dieser Zone ist abhängig von der Dotierung der beiden Bereiche und der intrinsischen Ladungsträgerdichte des Materials. Bei gleich hoher Dotierungsdichte in p- und n-Gebiet ist die Raumladungszone symmetrisch. Bei ungleichen Dotierungsdichten breitet sich die RLZ weiter in das weniger stark dotierte Gebiet aus.

Betrachtet man das Bändermodell dieser Anordnung, so haben sich durch den Diffusionsprozess die Fermi-Niveaus der beiden Kristalle angeglichen und es zeigt sich eine Krümmung der Energiebänder (Valenzband und Leitungsband) im Bereich des p-n-Übergangs. Die zuvor elektrisch neutralen Kristalle haben durch die zurückbleibenden, festen Ladungen nunmehr eine Raumladung erhalten, die im p-Kristall einen negativen und im n-Kristall einen positiven Pol erzeugt. Die dadurch entstandene Spannung wird Diffusionsspannung $\Phi _{\mathrm {D} }$ (englisch built-in voltage, U_bi) genannt. Auch sie ist abhängig von Dotierung und Material. Für einen p-n-Übergang aus Silizium beträgt die Diffusionsspannung für typische Dotierungen etwa 0,6 bis 0,7 V. Für die Ladungsträger stellt die Krümmung der Energiebänder einen Potenzialwall von der Energie $E=\Phi _{\mathrm {D} }\cdot e$ (e ist die Elementarladung) dar. Die Elektronen und Löcher müssen diesen Wall überwinden, um in den jeweils anderen Teil zu gelangen. Dafür benötigen sie Energie.

p-n-Übergang bei angelegter elektrischer Spannung

Die Energie zum Überwinden der Diffusionsspannung kann in Form elektrischer Energie zugeführt werden. Diese Energie vergrößert entweder den Potentialwall oder verkleinert ihn.

Durch Anlegen einer äußeren Spannung in Sperrrichtung (+ am n-Kristall, − am p-Kristall) wird das elektrische Feld der Sperrschicht verstärkt und die Ausdehnung der Raumladungszone vergrößert. Elektronen und Löcher werden von der Sperrschicht weggezogen. Es fließt nur ein sehr geringer Strom, erzeugt durch Minoritätsladungsträger (Sperrstrom), außer die Durchbruchspannung wird überschritten.

Bei Polung in Durchlassrichtung (+ am p-Kristall, − am n-Kristall) wird der Potentialwall abgebaut. Das elektrische Feld der Sperrschicht wird ab einer gewissen angelegten Spannung komplett neutralisiert und es ergibt sich mit dem von außen angelegten elektrischen Feld ein neues elektrisches Feld, welches Ladungstransport durch den gesamten Kristall erlaubt. Neue Ladungsträger fließen von der äußeren Quelle auf die Sperrschicht zu und rekombinieren hier fortwährend. Bei ausreichender angelegter Spannung fließt ein signifikanter elektrischer Strom.

Anwendung

Wie oben gezeigt, leitet der einfache p-n-Übergang elektrischen Strom in eine Richtung sehr gut, in die andere fast nicht. Eine solche Anordnung in Stromfließrichtung nennt man Diode (Halbleiterdiode). Sonderformen der Diode sind beispielsweise die Fotodiode und die Solarzelle. Bei diesen wird die entgegengesetzte elektrische Ladung der Raumladungszone verwendet, um generierte Elektron-Loch-Paare zu trennen. Fotodioden werden daher in Sperrrichtung betrieben. Dadurch hebt sich die Wirkung des Widerstandes auf, und der p-n-Übergang verliert seinen Einfluss auf die Elektron-Loch-Paare.

Eine direkte Anwendung des p-n-Übergangs in Querrichtung zum Stromfluss ist die Begrenzung von Leiterbahnen sowie ihre Abgrenzung voneinander. Die stets unvollkommene Abgrenzung führt zu den sogenannten Leckströmen.

Auch die meisten übrigen Halbleiterbauelemente beinhalten in klassischer Bauweise einen oder mehrere p-n-Übergänge zur Erzielung ihrer Funktion, z. B. im Bipolartransistor, Feldeffekttransistor (FET), MOS-FET, Halbleiterdetektor usw.

Berechnung

Die Weite der Raumladungszone in Abhängigkeit von der Donator- (N_D) und Akzeptorkonzentration (N_A) berechnet sich bei vollständiger Ionisierung der Dotieratome nach Shockley zu

W(U)={\sqrt {{\frac {2\cdot \varepsilon _{\mathrm {r} }\cdot \varepsilon _{0}}{e}}\left({\frac {1}{N_{\mathrm {A} }}}+{\frac {1}{N_{\mathrm {D} }}}\right)(\Phi _{D}-U)}}

,

wobei $\varepsilon _{0}$ die Permittivität des Vakuums, $\varepsilon _{\mathrm {r} }$ die relative Permittivität, $\Phi _{\mathrm {D} }$ die sich einstellende Diffusionsspannung am p-n-Kontakt, $e$ die Elektronenladung und $U$ die Spannung über der Diode ist.

Metall-Halbleiter-Übergänge

Werden statt zweier entgegengesetzt dotierter Halbleiter ein Metall mit einem p- oder n-dotierten Halbleiter kontaktiert, entsteht ein Metall-Halbleiter-Übergang. Bei normaler Dotierung des Halbleiters ist dies ein gleichrichtender Metall-Halbleiter-Kontakt. Er wird auch als Schottky-Kontakt bezeichnet und findet in Schottky-Dioden Anwendung. Bei hoher Dotierung oder bei Ausbildung von Mischkristallen am Kontakt (z. B. Al-Si oder WSi₂) entsteht ein Kontakt mit linearem Übertragungsverhalten, der als ohmscher Kontakt bezeichnet wird. Dies wird beim Drahtbonden von Halbleiterbauelementen mit metallischen Zuleitungen genutzt.

Weblinks

Commons: PN-junction diagrams – Sammlung von Bildern, Videos und Audiodateien

Philipp Laube: Der p-n-Übergang. In: halbleiter.org. 2009, abgerufen am 21. September 2009.
PN-Übergang aus wissenschaftlicher Sichtweise, iwenzo.de
3D-Animationen zum Thema (Memento vom 2. Mai 2008 im Internet Archive)
p-n-Übergang – Halbleiterdiode bei LEIFI mit Animationen (Schulniveau)

Einzelnachweise

Rudolf Müller: Grundlagen der Halbleiter-Elektronik. 5. Auflage. Springer-Verlag, Berlin 1987, ISBN 3-540-18041-9.
Joachim Rudolf: Knaurs Buch der modernen Chemie. Droemersche Verlagsanstalt, München 1971, S. 67 & 74.
Stefan Goßner: Grundlagen der Elektronik. 11. Auflage. Shaker-Verlag, Aachen 2019, ISBN 978-3-8440-6784-2, Kapitel 1 und 2.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Rudolf Müller: Grundlagen der Halbleiter-Elektronik. 5. Auflage. Springer-Verlag, Berlin 1987, ISBN 3-540-18041-9.

[2] Joachim Rudolf: Knaurs Buch der modernen Chemie. Droemersche Verlagsanstalt, München 1971, S. 67 & 74.

[3] Stefan Goßner: Grundlagen der Elektronik. 11. Auflage. Shaker-Verlag, Aachen 2019, ISBN 978-3-8440-6784-2, Kapitel 1 und 2.