Signalgeschwindigkeit

Die Signalgeschwindigkeit ist diejenige Geschwindigkeit, mit der sich ein Signal ausbreitet. Die Geschwindigkeit, mit der sich die erste Auslenkung einer Wellenfront bewegt, ist die Frontgeschwindigkeit. Diese Geschwindigkeit, und damit auch die Signalgeschwindigkeit, ist immer kleiner als die Lichtgeschwindigkeit. In Kabeln wird sie durch den Verkürzungsfaktor angegeben.

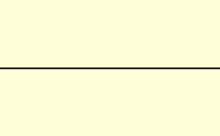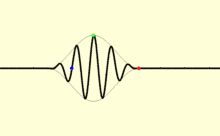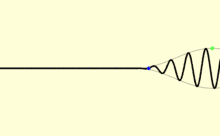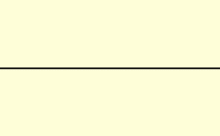
Propagation eines Wellenpaketes: Der blaue Punkt bewegt sich mit Phasengeschwindigkeit; der grüne mit Gruppengeschwindigkeit und der rote mit Frontgeschwindigkeit

Ein Signal, also eine Änderung eines Zustandes, lässt sich als Wellenpaket beschreiben. Die Geschwindigkeit, mit der sich die Einhüllende eines solchen Wellenpaketes bewegt, ist die Gruppengeschwindigkeit. Sie ist im Allgemeinen, insbesondere wenn die Phasengeschwindigkeit stark von der Frequenz abhängig oder die Absorption nicht vernachlässigt werden kann, von der Signalgeschwindigkeit zu unterscheiden.

Frontgeschwindigkeit und Gruppengeschwindigkeit

Im 19. Jhdt. nahm Lord Rayleigh an, dass eine Welle Information und Energie mit Gruppengeschwindigkeit überträgt.[1] In Ausbreitungsmedien mit anomaler Dispersion ist die Gruppengeschwindigkeit proportional zum Betrag der Dispersion. Dabei gibt es keine prinzipielle physikalische Grenze; so ist möglich, dass sich das Zentrum eines Wellenpakets mit Überlichtgeschwindigkeit bewegt.

Gemäß der speziellen Relativitätstheorie ist jedoch die Lichtgeschwindigkeit die höchste Geschwindigkeit, mit der Information übertragen werden kann. Woldemar Voigt zeigte daher anhand der Telegraphengleichung, dass die Geschwindigkeit einer Wellenfront im Fall dieser Telegraphengleichung kleiner als die Gruppengeschwindigkeit ist, und damit die Signalgeschwindigkeit von der Gruppengeschwindigkeit unterschieden werden muss.[2]

Die Front einer Welle ist durch eine Oberfläche definiert, hinter der zu einem gewissen Zeitpunkt die Amplitude einer Welle identisch Null ist.

Frontgeschwindigkeit und Lichtgeschwindigkeit

Dass die Frontgeschwindigkeit immer kleiner als die Lichtgeschwindigkeit ist, lässt sich zeigen anhand eines allgemeinen Signals der Form[1]

\Psi (x=0,t)=\Theta (t)e^{\mathrm {i} \omega t}

mit der Heaviside-Funktion $\Theta (t)$ .

Wenn sich die Wellenfront $t=0$ dieser Welle nicht mit Überlichtgeschwindigkeit bewegen kann, so muss für eine Distanz $x>ct$ die Wellenfunktion $\Psi (x,t)$ Null sein. Für die Wellenfunktion

\Psi (x,t)=\int _{-\infty }^{\infty }\mathrm {d} t'\,G(x,t-t')\Psi (0,t')

mit der Greensfunktion

G(x,\tau )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\mathrm {d} \omega \,e^{\mathrm {i} \omega \left(n(\omega ){\frac {x}{c}}-\tau \right)}

lässt sich dies mithilfe des Residuensatzes zeigen.

Da für große Frequenzen $\omega \to \infty$ der Brechungsindex $n=1$ ist, bleibt dort $e^{\mathrm {i} \left({\frac {x}{c}}-t\right)}$ als Integrand über. Für $x>ct\Leftrightarrow {\tfrac {x}{c}}-t>0$ lässt sich dies als Kurvenintegral über die obere Hälfte der komplexen Ebene schreiben. Da der Brechungsindex dort aber analytisch ist (also keine Singularitäten besitzt), ist das Integral Null.

Literatur

Léon Brillouin: „Wave propagation and group velocity“, Academic Press Inc., New York, 1960

Weblinks

gregegan.customer.netspace.net.au – Applet, das Gruppen-, Phasen- und Signalgeschwindigkeit einer Welle verdeutlicht.
Zur Geschichte der Begriffe bei Sommerfeld, Brillouin, Duke University

Einzelnachweise

P.W. Milonni: Fast Light, Slow Light and Left-Handed Light. CRC Press, 2004, ISBN 1-4200-3433-2, S. 26 (eingeschränkte Vorschau in der Google-Buchsuche).
Léon Brillouin: Wave Propagation and Group Velocity. Academic Press, 2013, ISBN 1-4832-7601-5, S. 10 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[milonni-1] P.W. Milonni: Fast Light, Slow Light and Left-Handed Light. CRC Press, 2004, ISBN 1-4200-3433-2, S. 26 (eingeschränkte Vorschau in der Google-Buchsuche).

[2] Léon Brillouin: Wave Propagation and Group Velocity. Academic Press, 2013, ISBN 1-4832-7601-5, S. 10 (eingeschränkte Vorschau in der Google-Buchsuche).