Zustandsgröße (Systemtheorie)

Der Begriff Zustandsgröße oder Zustandsvariable wird in der Systemtheorie zur Systembeschreibung in der Zustandsraumdarstellung benutzt.

Die Zustandsvariablen der Zustandsraumdarstellung beschreiben physikalisch den Energiegehalt der in einem technischen dynamischen System enthaltenen Speicherelemente. Sie bedeuten z. B. Spannung an einem Kondensator, Strom in einer Induktivität, potentielle und kinetische Energieanteile bei einem Feder-Masse-Dämpfungssystem. Die Anzahl $n$ der Zustandsvariablen $x_{1}(t)\cdots x_{n}(t)$ des Zustandsvektors ${\underline {x}}(t)$ ist die Dimension des Zustandsraumes. Technische Anwendung: Regelungstechnik.

Zustandsgrößen der Zustandsraumdarstellung

Die Theorie des Zustandsraumes stammt aus den USA der 1960er Jahre von dem Mathematiker und Stanford-Universitätslehrer Rudolf E. Kalman.

Ein dynamisches System ist eine abgegrenzte zeitabhängige Funktionseinheit, die durch ihre Signaleingänge und Signalausgänge in einer Wechselwirkung mit der Umwelt steht. Das System kann ein mechanischer Körper, ein elektrisches Netzwerk {Netzwerk (Elektrotechnik)}, aber auch ein biologischer Vorgang oder ein Bestandteil der Volkswirtschaft sein.

Die Zustandsraumdarstellung ist eine Systembeschreibung eines meist technischen Systems mit mehreren Energiespeichern und mindestens einer Eingangsgröße und einer Ausgangsgröße. Die Eingangsgröße kann den Wert Null haben, in diesem Fall ist das System mit seinen Anfangswerten der Energiespeicher zum Zeitpunkt t = 0 für t > 0 sich selbst überlassen und strebt mit seiner Ausgangsgröße nach genügend langer Zeit den Wert Null an (im Fall eines stabilen Systems, Beispiel gedämpftes Federpendel). Physikalisch betrachtet ist der Zustand eines dynamischen Systems durch den Energiegehalt der im System vorhandenen Energiespeicher bestimmt. Die Zustandsgrößen beschreiben den Energiegehalt der im System enthaltenen Speicherelemente.

Symbolisches Blockschaltbild eines Modells eines Übertragungssystems mit Zustandsvariablen

x_{i}(t)

in der Zustandsraumdarstellung für ein Eingrößensystem.

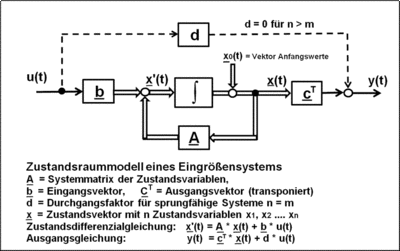
Zwei Wege führen zu einem Zustandsraummodell eines dynamischen Systems:

durch Aufstellen des physikalischen Wirkungszusammenhanges mittels Differentialgleichungen 1. Ordnung,
durch Umwandlung einer Differentialgleichung höherer Ordnung in ein System gekoppelter Differentialgleichungen 1. Ordnung.

Sämtliche Beziehungen der Zustandsgrößen, der Eingangsgrößen und Ausgangsgrößen einer Zustandsraummodells werden in Form von Matrizen und Vektoren dargestellt. Das Zustandsraummodell wird durch zwei Gleichungen – die Zustandsdifferentialgleichung und die Ausgangsgleichung – beschrieben.

Die Zustandsvariablen $x_{i}(t)$ sind bei gegebener Ausgangsgleichung der Zustandsraumdarstellung (bei n > m ist der Durchgangsfaktor d = 0) direkt ablesbar.

{\begin{bmatrix}y(t)\\\end{bmatrix}}=\underbrace {\begin{bmatrix}c_{1}&...&c_{n}\\\end{bmatrix}} _{Ausgangs-Vektor}\ \cdot \underbrace {\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\\vdots \\x_{n}(t)\\\end{bmatrix}} _{Zustd.-Vektor}

Nachfolgend wird die Entstehung, Definition und Anwendung der Zustandsvariablen $x_{i}(t)$ , die in dem Zustandsvektor ${\underline {x}}(t)$ zusammengefasst sind, behandelt.

Entstehung der Zustandsvariablen

Typische physikalische Größen, die als Zustandsvariablen wie Ströme, Spannungen, Winkel, Wege, Geschwindigkeiten, Beschleunigungen, Kräfte, Temperatur an Energiespeichern wie Kapazitäten, Induktivitäten, Massen und Federn auftreten, geben das zeitliche Verhalten an den Speicherelementen in Abhängigkeit von den Eingangssignalen oder Anfangswerten wieder.

Ein lineares dynamisches System wird durch eine gewöhnliche Differentialgleichung mit konstanten Koeffizienten beschrieben.

a_{n}\cdot y^{(n)}(t)+\ \cdots \ +a_{2}\cdot {\ddot {y}}(t)+a_{1}\cdot {\dot {y}}(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)+b_{1}\cdot {\dot {u}}(t)+b_{2}\cdot {\ddot {u}}(t)+\ \cdots \ +b_{m}\cdot u^{(m)}(t)

Der höchste Grad der Ableitung von $y(t)\;$ gibt die Anzahl der Speicherelemente des Systems wieder. Diese Differentialgleichung kann mit Hilfe der Laplace-Transformation als Übertragungsfunktion definiert werden:

Übertragungsfunktion der Polynomdarstellung und der Zerlegung in die Pol-Nullstellen-Darstellung mit reellen Linearfaktoren:

G(s)={\frac {Y(s)}{U(s)}}={\frac {b_{m}s^{m}+\ldots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{n}s^{n}+\ldots +a_{2}s^{2}+a_{1}s+a_{0}}}:=k\cdot {\frac {(s-s_{n1})(s-s_{n2})\dotsm (s-s_{nm})}{(s-s_{p1})(s-s_{p2})\dotsm (s-s_{pn})}}

Dabei bedeuten m = Anzahl der Nullstellen $s_{n}$ , n = Anzahl der Pole $s_{p}$ , s = Laplace-Variable.

Zustandsvariablen entstehen aus den Polen des Übertragungssystems:

Die Zustandsvariablen eines linearen Systems n-ter Ordnung mit n Energiespeichern entstehen immer aus den Polen der Übertragungsfunktion. Hat das Übertragungssystem auch Nullstellen – also differenzierende Anteile – so werden die Zustandsvariablen mit den Koeffizienten der Ableitungen der Eingangsgröße u(t) zu der Ausgangsgröße y(t) addiert. Die Pole einer Übertragungsfunktion bestimmen die Geschwindigkeit der Systembewegung und der Stabilität. Die Nullstellen einer Übertragungsfunktion haben nur Einfluss auf die Amplituden des Systems.

Die Zustandsvariablen eines mathematischen Modells eines dynamischen Systems, einer Regelstrecke, können aus der gewöhnlichen systembeschreibenden Differentialgleichung bestimmt werden. Grundlage der Lösung der Differentialgleichung ist der Signalflussplan mit der grafischen Darstellung der Regelungsnormalform. Dabei werden die Terme der Ableitungen der Ausgangsgröße y(t) jeweils integriert und mit den zugehörigen Koeffizienten auf den Systemeingang zurückgeführt.

Für jede Ableitung von y(t) der Differenzialgleichung wird die Bezeichnung der Zustandsgrößen x(t) wie folgt eingeführt:

x_{1}(t)=y(t)

x_{2}(t)={\frac {dy}{dt}}={\dot {y}}

x_{3}(t)={\ddot {y}}

x_{n}(t)={\frac {dy^{(n-1)}}{d^{(n-1)}t}}=y^{(n-1)}(t)

In dem Zustandsvektor ${\underline {x}}(t)$ sind alle Zustandsvariablen $x_{i}(t)$ zusammengefasst. Zu einem beliebigen Zeitpunkt t₍₀₎ sind in dem Zustandsvektor ${\underline {x}}(t)$ alle Informationen des dynamischen Übertragungssystems enthalten.

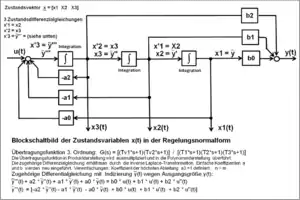
Blockschaltbild des Signalflussplanes eines Übertragungssystems 3. Ordnung in der Regelungsnormalform.

Regelungsnormalform

Bei den Zustandsbeschreibungen mit Normalformen nehmen die Zustandsgleichungen besonders einfache und zweckmäßige Formen für bestimmte Berechnungen an. Für die Normalformen wird von der Systembeschreibung des linearen Übertragungssystems durch die Differenzialgleichung oder zugehörige Übertragungsfunktion ausgegangen.

Die Signalstruktur der Regelungsnormalform stellt sich als ein analoges zeitkontinuierliches System dar, das mit der Eingangsgröße $u(t)$ die Lösung der Differentialgleichung $y(t)$ wiedergibt und gleichzeitig die Zustandsvariablen $x_{1}(t),x_{2}(t)\cdots x_{n}(t)$ zeigt.

Das Blockschaltbild der Regelungsnormalform zeigt die Umsetzung und Lösung der Differentialgleichung in die physikalischen analogen Signalflüsse der Zustandsgrößen einschließlich der Ausgangsgröße bei gegebener Eingangsgröße. Die Lösungsstruktur ergibt sich aus der Umformung der Differentialgleichung mit der Freistellung der höchsten Ableitung $a_{n}\cdot y^{(n)}(t)$ von y(t). Alle Ableitungen werden in der Reihenfolge der Ordnung durch Integratoren integriert und mit den zugehörigen Koeffizienten wieder auf die höchste Ableitung zurückgeführt und subtrahiert. Die Ausgänge der Integratoren bilden die Zustandsvariablen. y(t) ist neben den Zustandsvariablen die Systemausgangsgröße.

Man kann die Regelungsnormalform als eine Weiterentwicklung der in der Analogrechentechnik bekannten Verfahren zur Lösung einer Differentialgleichung n-ter Ordnung mit n Integratoren betrachten. Die Signalflüsse können bei Kenntnis der Koeffizienten der Zustandsvariablen direkt mittels numerischer Berechnung für beliebige Eingangssignale ermittelt und grafisch dargestellt werden.

Liegen Anfangswerte der Systemspeicher vor, können diese Werte auf die Integratoren des Signalflussplanes der Regelungsnormalform gesetzt werden.

In dem Blockschaltbild der Regelungsnormalform werden die Ableitungen von ${\tilde {y}}(t)$ durch die Zustandsvariablen $x_{1}\cdots x_{n}$ ersetzt, so dass ${\tilde {y}}(t)$ nicht mehr in Erscheinung tritt.

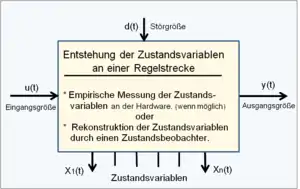
Schnittstelle einer Regelstrecke im Zustandsraum.

Zeitliches Verhalten der Zustandsvariablen in einer Regelstrecke

Der zeitliche Verlauf der Zustandsvariablen als Folge eines Eingangssprungs u(t) = 1 an dem Modell zeigt den Vorteil der Behandlung des Systems im Zustandsraum gegenüber einer klassischen „Ausgangsrückführung“ des Systems. Die Zustandsvariablen x(t) erscheinen zeitlich früher als die Ausgangsgröße y(t). Dieses Verhalten wird beim Zustandsregelkreis genutzt, indem die Zustandsvariablen auf eine Soll-Ist-Differenz mit der Führungsgröße w(t) zurückgeführt werden.

Regelstrecken bestehen allgemein aus einer bereits vorhandenen Hardware und haben mindestens einen Systemeingang $u(t)$ und einen Systemausgang $y(t)$ . Gegebenenfalls können an mehreren Eingriffsstellen Störgrößen $d(t)$ in verschiedensten Signalformen angreifen. Häufig wird die Systembeschreibung im Laplace-transformierten s-Bereich als Übertragungsfunktion $G(s)$ beschrieben.

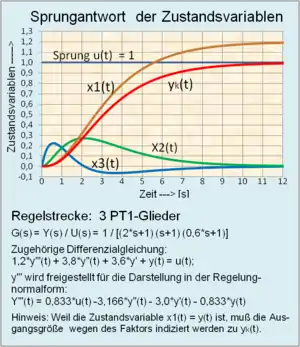
Sprungantwort der Zustandsvariablen einer PT3-Regelstrecke.

Man kann die vorgegebene Hardware der Regelstrecke als Eingrößensystem auch im Zustandsraum als Funktionsblock beschreiben. In diesem Fall hat der Block mindestens einen Systemeingang $u(t)$ , einen Systemausgang $y(t)$ und mehrere Ausgänge der Zustandsvariablen $x_{i}(t)$ und gegebenenfalls Störgrößeneingänge $d(t)$ .

Das Systemverhalten des Funktionsblocks kann durch gewöhnliche Differentialgleichungen oder Übertragungsfunktionen beschrieben und in die Regelungsnormalform der Zustandsraumdarstellung überführt werden. Die Integratoren der Regelungsnormalform können für einen betrachteten Zeitpunkt $t_{0}$ in der Ruhelage den Wert Null annehmen, sie können aber auch Anfangswerte $y_{0}^{(n)}(t)>0$ für mehrere Ableitungen enthalten.

Selten ist die Differentialgleichung oder die Übertragungsfunktion der Regelstrecke bekannt, man muss das Übertragungsverhalten identifizieren. Die für den Regler benötigten Zustandsvariablen $x_{i}(t)$ müssen ermittelt werden durch:

In der Praxis können die Zustandsvariablen an der Hardware einer Regelstrecke gemessen werden, was nicht immer möglich ist.
Beobachter durch Rekonstruktion der Zustandsvariablen, wenn die Strecke beobachtbar ist. Die Regelstrecke muss steuerbar sein.
Alle Zustandsvariablen müssen verfügbar sein.
Pol-Nullstellenkompensation im Zustandsraum ist nicht erlaubt, weil Informationsverlust.

Zustandsregler

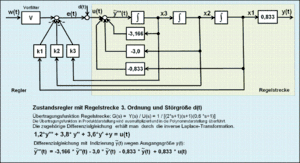
Blockschaltbild eines Zustandsreglers für eine Regelstrecke 3. Ordnung eines Eingrößensystems.

Als Entwurfsstrategie für die Bestimmung der Bewertungsfaktoren des Zustandsreglers gilt die Polzuweisung (Polvorgabe) des geschlossenen Regelkreises.

Simulationen eines Zustandsregelkreises können mit einem guten Modell der Regelstrecke an einem programmierbaren Rechner einfach durchgeführt werden. Die Beschreibung des Signalflussplanes der Regelstrecke und des Reglers im Zustandsraum kann sowohl in Form von Matrizen als auch mit Differenzengleichungen erfolgen. Je nach Höhe der Ordnung der Differentialgleichung werden alle Zustandsgrößen einem Zustandsregler zugeführt, der auf den Eingang des Zustandsraummodells der Regelstrecke wirkt. Durch die Rückführung sämtlicher Zustandsvariablen entsteht ein mehrschleifiger Regelkreis.

Es ist auch möglich, die Verstärkungsfaktoren des Zustandsreglers empirisch zu bestimmen. Die Regelstrecke in der Regelungsnormalform und der aus einer Mehrfach-Subtraktionsstelle mit dem Vorfilter V bestehende Zustandsregler können durch Simulation mittels Differenzengleichungen an einem Personal Computer nachgebildet werden.

Durch die Hintereinanderschaltung der Integratoren laut Blockschaltbild ist nur die Zustandsvariable $x1(t)$ eine stationäre Größe >0, wenn die Eingangsgröße $u(t)$ > 0 konstant ist. Alle anderen Zustandsvariablen – eine stabile Regelstrecke vorausgesetzt – streben gegen den Wert Null. Damit ist bei grafischer Darstellung der Systemausgangsgröße $y(t)$ der Simulation der stationäre Zustand für das Einschwingverhalten für einen noch festzulegenden Faktor $K_{1}(x1)$ gegeben. Die Verstärkungsfaktoren können möglichst hoch gewählt werden, z. B. 20-fach bis 100-fach, jedoch ist zu berücksichtigen, dass die Regelstrecke in der Realität ein Hardware-System ist, das keine beliebig hohen Stellwerte des Reglers aufnehmen kann.

Strategie der Bestimmung der Verstärkungsfaktoren bei einer Regelstrecke mit drei Zustandsgrößen:

Die Führungsgröße $w(t)$ wird auf einen normierten Sprung $1(t)$ eingestellt.
Die Verstärkungsfaktoren $K_{1}(x1)$ ; $K_{2}(x2)$ , $K_{3}(x3)$ und $K_{V}$ des Vorfilters V werden auf z. B. auf 20 eingestellt.
Die Verstärkungsfaktoren $K_{2}(x2)$ und $K_{3}(x3)$ werden solange geändert, bis der gewünschte Einschwingvorgang z. B. überschwingungsfrei erfolgt.
Mit dem Faktor $K_{V}$ des Vorfilters wird der stationäre Zustand von $y(t)$ auf das Niveau 1 eingestellt.

Der lineare Zustandsregler bewertet die einzelnen Zustandsvariablen der Regelstrecke mit Faktoren und summiert die so entstandenen Zustandsprodukte zu einem Soll-Istwert-Vergleich.

u(t)=w(t)-x_{1}\cdot k_{1}-x_{2}\cdot k_{2}-\cdots -x_{n}\cdot k_{n}=w(t)-{\underline {x}}(t)\cdot {\underline {k}}(t)

Es handelt sich bei diesem Zustandsregler nicht um einen P-Regler, wenngleich ein solcher Eindruck laut Signalflussplan entstehen könnte. Durch die mit dem Regler zurückgeführten Zustandsvariablen mit Bewertungsfaktoren durchlaufen noch einmal die Rechenschaltung zur Lösung der Differenzialgleichung mit n Integratoren und bilden neue Kreisvariablen, wodurch differenzierendes Verhalten entsteht. Deshalb entspricht die Wirkung der zurückgeführten Zustandsgrößen je nach Höhe der Ordnung n der Differenzialgleichung der Strecke der eines $PD_{(n-1)}$ -Reglers.[1]

Als Entwurfsstrategie für die Bestimmung der Bewertungsfaktoren des Zustandsreglers gilt die Polzuweisung (Polvorgabe) des geschlossenen Regelkreises oder auch empirisch. Durch die Hintereinanderschaltung der Integratoren ist nur die Zustandsvariable x1(t) = y(t) eine stationäre Größe >0, wenn die Eingangsgröße u(t) konstant ist. Alle anderen Zustandsvariablen – eine stabile Regelstrecke vorausgesetzt – streben gegen den Wert Null.

Ein Vorfilter vor dem Soll-Ist-Vergleich korrigiert den statischen Fehler zwischen w(t) und y(t), weil es sich hier um eine Zustandsrückführung und nicht um eine Ausgangsrückführung handelt. Das Vorfilter kann entfallen, wenn ein zusätzlicher PI-Regler anstelle des Vorfilters eingesetzt wird, der die statische Regelabweichung minimiert.

Die Regelgüte einer Regelung mit Zustandsvariablen kann durch kein anderes Regelverfahren erreicht werden.

Siehe auch

systemeigene Größe

Einzelnachweise

Zustandsregler durch Polvorgabe. In: Oliver Nelles: Vorlesungsmanuskript Meß- und Regelungstechnik II. Universität Siegen, 4. Mai 2010.

Literatur

Jan Lunze: Regelungstechnik 1: Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen. 7. Auflage. Springer, 2008, ISBN 3-540-68907-9.
H. Lutz, W. Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. Europa-Verlag, 2021, ISBN 978-3-8085-5870-6.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Zustandsregler durch Polvorgabe. In: Oliver Nelles: Vorlesungsmanuskript Meß- und Regelungstechnik II. Universität Siegen, 4. Mai 2010.