Netzwerk (Elektrotechnik)

In der theoretischen Elektrotechnik versteht man unter einem Netzwerk verschieden komplexe mathematische Modelle einer elektrischen Schaltung, oder Teile einer solchen Schaltung, welche der Modellbildung im Rahmen der Systemtheorie wie der Schaltungsanalyse und Schaltungssynthese dienen.

Allgemeines

Verschiedene Schaltsymbole, wie sie in der grafischen Darstellung von elektrischen Netzwerken Verwendung finden

Die grafische Darstellung elektrischer Bauelemente erfolgt in Form von Schaltplänen in einer abstrakten Weise. Werden im Rahmen der Modellbildung elektrische Schaltungen zur leichteren Untersuchung auf ihre wesentlichen Bauelemente und Parameter reduziert, spricht man auch von einer Ersatzschaltung. Der Umfang der Reduzierung wird durch die jeweilige Anwendung bestimmt, unter der Beachtung, dass dabei der Fehler in der Modellbildung nicht zu groß werden darf.

Sind in einem Netzwerk die Beziehungen zwischen den auftretenden Spannungen und Strömen linear, so spricht man von linearen (elektrischen) Netzwerken. Eine weitere Vereinfachung erlauben die zeitinvarianten Netzwerke, auch als lineares zeitinvariantes System bezeichnet. In diesem Fall sind die Parameter keiner zeitlichen Abhängigkeit unterworfen, es gilt unter anderem der Überlagerungssatz. Dadurch sind weitere systematische Methoden zur Analyse anwendbar, wie das Maschenstromverfahren und das Knotenpotentialverfahren.

Beispiele verschiedenartiger einfacher Netzwerke sind unter anderem Widerstandsnetzwerke, Spannungs- und Stromteiler oder Netzwerke in Form verschiedenartiger Filtertopologien, elektrische Leitungen. Ist der konkrete innere Aufbau eines Netzwerkes nicht von Interesse, sondern nur das Verhalten an seinen Anschlüssen nach außen, die Anschlüsse werden in diesem Zusammenhang auch als Tor bezeichnet, erfolgt die Beschreibung durch das Verhalten an diesen Anschlüssen. Eine wichtige Beschreibungsform stellt dabei das sogenannte Zweitor dar.

Modelle

Je nach Anforderung gibt es verschiedene Netzwerkmodelle. Im Folgenden werden die zwei Modelle, mit konzentrierten Bauelementen und mit verteilten Bauelementen, dargestellt.

Netzwerkmodell mit konzentrierten Elementen

Das Netzmodell mit konzentrierten Elementen, englisch lumped element model, beschreibt elektrische Schaltkreise mit einzelnen Elementen in welchem die bestimmenden Parameter konzentriert sind. Die Verbindungsleitungen sind als ideal, also ohne Verluste oder sonstige Einflussnahme, angenommen. Feldgrößen wie beispielsweise das elektrische oder die magnetische Flussdichte kommen nicht direkt vor. Die physikalischen Eigenschaften des Netzwerkes wird durch die Eigenschaften und Parameter in den einzelnen Bauelementen in Näherung abgebildet, was die Modellbeschreibung dieses Netzwerkmodells vereinfacht und unter anderem Anwendung im Rahmen der Kirchhoffschen Regeln (u. a. Maschenregel und Knotenregel) findet. Beispiele für konzentrierte Elemente sind unter anderem ideale Widerstände, Kondensatoren, Spulen und Spannungs- und Stromquellen.

In mathematischen Bezug kann durch diese Vereinfachung die Zustandsraumdarstellung auf eine endliche Anzahl von Parametern reduziert werden. Die partiellen Differentialgleichungen werden dabei auf gewöhnliche Differentialgleichungen mit einer endlichen Anzahl von Parametern überführt.

Die Gültigkeit dieses Modells und die Vereinfachung ist in Näherung dann gegeben, wenn die Bedingung

l_{c}\ll \lambda

erfüllt ist. $l_{c}$ beschreibt die charakteristische räumliche Ausdehnung des Netzwerkes, $\lambda$ die in dem Netzwerk auftretenden Wellenlängen. Eine andere Möglichkeit um die Zulässigkeit des Modells zu prüfen ist die Signallaufzeiten innerhalb des Netzwerkes zu betrachten: Können diese Signallaufzeiten in einem Anwendungsfall vernachlässigt werden, kann das Netzwerkmodell mit konzentrierten Elementen verwendet werden.

Kommt die charakteristische räumliche Ausdehnung $l_{c}$ des Netzwerkes in die Größenordnung der darin auftretenden Wellenlänge $\lambda$ , der Übergang ist fließend und durch zunehmenden Fehler im Modell gekennzeichnet, muss auf das Netzwerkmodell mit verteilten Elementen übergangen werden.

Netzwerkmodell mit verteilten Elementen

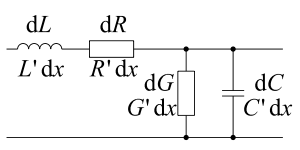
Netzwerkmodell eines infinitesimalen Leitungsstücks mit seinen Leitungsbelägen

Das Netzwerkmodell mit verteilten Elementen, englisch distributed element model, oder auch als Übertragungsleitungsmodell bezeichnet, beschreibt elektrische Schaltkreise in infinitesimal kleinen und räumlich quasi „verschmierten“ Bauelementen in Form von Leitungsbelägen. Die dabei auftretenden Beläge sind der Widerstandsbelag R', der Kapazitätsbelag C', der Induktivitätsbelag L' und der Ableitungsbelag G'. Auch die Verbindungsleitungen innerhalb des Netzwerkes werden aus diesen räumlich verteilten Belägen modelliert und Leitungen werden nicht mehr als ideal angenommen. Im Gegensatz zu dem einfacheren Netzwerkmodell mit konzentrierten Elementen können auch die auf der Vereinfachung basierenden Verfahren wie die Kirchhoffsche Regeln nicht mehr angewendet werden, stattdessen erfolgt die Systembeschreibung über partielle Differentialgleichungen. Auch ist eine grafische Darstellung in Schaltplänen mit konzentrierten Bauelementen im Allgemeinen nicht mehr möglich.

Anwendung dieses Modells ist unter anderem die Leitungstheorie, wie sie unter anderem im Rahmen der Telegraphengleichung zum Ausdruck kommt. Die Anwendung dieses Netzwerkmodells kann auch bei kleinen räumlichen Strukturen mit der charakteristischen Ausdehnung $l_{c}$ notwendig sein, wenn die dabei auftretenden Wellenlängen $\lambda$ in etwa in der gleichen Größenordnung oder darunter liegen. Dieser Fall ist gleichbedeutend mit dem Auftreten hoher Frequenzen. Aus diesem Grund findet das Netzwerkmodell mit verteilten Elementen im Bereich der Hochfrequenztechnik, wie der Modellierung von Streifenleitungen, Anwendung.

Zusammenhang

Neben den verschiedenen Netzwerkmodellen können die physikalischen Zusammenhänge in elektrischen Netzwerken auch mit Hilfe der Feldtheorie, ausgehend von den Maxwell-Gleichungen und Materialgleichungen der Elektrodynamik und mit Feldgrößen wie dem elektrischen Feld oder der magnetische Flussdichte, beschrieben werden. Die dabei auftretenden partiellen Differentialgleichungen sind im Regelfall bis auf einige Problemstellungen nicht mehr analytisch lösbar. Es kommen numerische Lösungsverfahren wie die Finite-Elemente-Methode zur Anwendung.

Literatur

Karl Küpfmüller, Wolfgang Mathis, Albrecht Reibiger: Theoretische Elektrotechnik und Elektronik. 18. Auflage. Springer, 2008, ISBN 978-3-540-78589-7, 4. Kapitel.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.