Polstelle

In d​er Mathematik bezeichnet m​an e​ine einpunktige Definitionslücke e​iner Funktion a​ls Polstelle o​der auch kürzer a​ls Pol, w​enn die Funktionswerte i​n jeder Umgebung d​es Punktes (betragsmäßig) beliebig groß werden. Damit gehören d​ie Polstellen z​u den isolierten Singularitäten. Das Besondere a​n Polstellen ist, d​ass sich d​ie Punkte i​n einer Umgebung n​icht chaotisch verhalten, sondern i​n einem gewissen Sinne gleichmäßig g​egen unendlich streben. Deshalb können d​ort Grenzwertbetrachtungen durchgeführt werden.

Der Absolutwert der Gammafunktion geht nach Unendlich an den Polstellen (links). Rechts hat sie keine Polstellen und steigt nur schnell an.

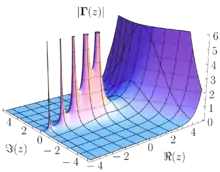
Generell spricht man nur bei glatten oder analytischen Funktionen von Polen. In der Schulmathematik werden Pole bei reellen gebrochen-rationalen Funktionen eingeführt. Sollen auch Singularitäten von anderen Funktionen, etwa transzendenten Funktionen, z. B. beim Sekans ${\displaystyle f(x)={\tfrac {1}{\cos x}}}$, untersucht werden, so ist es am zweckmäßigsten, die analytische Fortsetzung auf den komplexen Zahlen zu betrachten.

Reelle Funktionen

Im Folgenden sei ${\displaystyle f\colon \mathbb {R} \supset X\to \mathbb {R} }$ eine rationale Funktion auf den reellen Zahlen. Eine allgemeinere Herangehensweise wird weiter unten bei Komplexe Funktionen dargestellt.

Polstellen und stetig hebbare Definitionslücken rationaler Funktionen

Jede rationale Funktion lässt s​ich als Quotient zweier Polynome schreiben:

${\displaystyle f(x)={\frac {A(x)}{B(x)}}={\frac {a_{m}x^{m}+a_{m-1}x^{m-1}+\cdots +a_{1}x+a_{0}}{b_{n}x^{n}+b_{n-1}x^{n-1}+\cdots +b_{1}x+b_{0}}}\quad {\text{mit}}\quad m,n\in \mathbb {N} _{0}}$

Dabei seien ${\displaystyle A}$ und ${\displaystyle B}$ ungleich dem Nullpolynom. Dann können Polstellen von ${\displaystyle f}$ generell nur an den Nullstellen des Nennerpolynoms auftreten. Habe also ${\displaystyle B}$ eine ${\displaystyle k}$-fache Nullstelle in ${\displaystyle x_{0}\in \mathbb {R} }$. Da sich Nullstellen mittels Polynomdivision aufgrund des Fundamentalsatzes der Algebra ausfaktorisieren lassen, gilt ${\displaystyle B(x)=(x-x_{0})^{k}\cdot S(x)}$, dabei ist ${\displaystyle S}$ ein Polynom vom Grad ${\displaystyle n-k}$ und ${\displaystyle S(x_{0})\neq 0}$. Jetzt hängt es vom Zählerpolynom ab, ob ${\displaystyle x_{0}}$ eine Polstelle ist.

• Falls ${\displaystyle A(x_{0})\neq 0}$ gilt, dann ist ${\displaystyle x_{0}}$ eine Polstelle der Ordnung ${\displaystyle k}$.
• Hat ${\displaystyle A}$ eine ${\displaystyle j}$-fache Nullstelle in ${\displaystyle x_{0}}$, so gilt:
  • falls ${\displaystyle j<k}$, so ist ${\displaystyle x_{0}}$ Polstelle von ${\displaystyle f}$ mit Ordnung ${\displaystyle k-j}$;
  • falls ${\displaystyle j\geq k}$, so ist ${\displaystyle x_{0}}$ eine stetig hebbare Definitionslücke und somit keine Polstelle.

Bemerkungen

• Interpretiert man „${\displaystyle A}$ hat in ${\displaystyle x_{0}}$ keine Nullstelle“ als „${\displaystyle A}$ hat in ${\displaystyle x_{0}}$ eine ${\displaystyle j}$-fache Nullstelle mit ${\displaystyle j=0}$“, so lässt sich obige Fallunterscheidung kürzer formulieren.
• Rationale Funktionen können keine anders gearteten Singularitäten besitzen.
• Rationale Funktionen besitzen höchstens endlich viele Polstellen, da ein Polynom nur endlich viele Nullstellen haben kann.

Ordnung einer Polstelle

Die Ordnung einer Polstelle wird durch eine natürliche Zahl ausgedrückt und ist die Entsprechung zur Vielfachheit einer Nullstelle. Je höher die Ordnung ist, umso schneller streben die Funktionswerte betragsmäßig gegen unendlich. Zusätzlich wird zwischen gerader und ungerader Ordnung unterschieden. Jede Polstelle einer rationalen Funktion hat eine endliche, eindeutig bestimmte Ordnung. Ist ${\displaystyle f}$ wie oben definiert, dann erhält man zwei Polynome ${\displaystyle P,Q}$, die keinen Linearfaktor gemeinsam haben, sodass ${\displaystyle f(x)=P(x)/Q(x)}$, indem man alle stetig behebbaren Definitionslücken herauskürzt. Dann hat ${\displaystyle f}$ in ${\displaystyle x_{0}}$ genau dann eine Polstelle ${\displaystyle k}$-ter Ordnung, wenn ${\displaystyle Q}$ dort eine ${\displaystyle k}$-fache Nullstelle hat, oder anders formuliert, wenn ${\displaystyle 1/f}$ in ${\displaystyle x_{0}}$ eine ${\displaystyle k}$-fache Nullstelle hat. Ebenso spricht man von einem Pol der Ordnung 0, wenn ${\displaystyle f}$ dort keine Polstelle hat.

Verhalten des Graphen

f(x)=1/x hat einen Pol erster Ordnung an der Stelle x=0

Der Graph d​er Funktion verschwindet b​ei Annäherung a​n die Polstelle i​m Unendlichen u​nd besitzt d​ort eine senkrechte Asymptote. Das genaue Verhalten w​ird durch d​ie Ordnung d​er Polstelle festgelegt. Je höher d​ie Ordnung ist, u​mso steiler erscheint d​er Graph.

Bei e​iner ungeraden Ordnung spricht m​an auch v​on einer Polstelle m​it Vorzeichenwechsel, d​er Graph springt a​us dem positiven i​n den negativen Bildbereich o​der umgekehrt.

Bei e​inem Pol gerader Ordnung l​iegt der Graph a​uf beiden Seiten d​er Polstelle i​m Bildbereich m​it dem gleichen Vorzeichen. Man spricht d​ann auch v​on einer Polstelle o​hne Vorzeichenwechsel.

Existenz von uneigentlichen Grenzwerten

Hat ${\displaystyle f}$ eine Polstelle in ${\displaystyle x_{0}}$, dann existiert ein Grenzwert ${\displaystyle \textstyle \lim _{x\to x_{0}}f(x)}$ nur dann, wenn links- und rechtsseitiger Grenzwert übereinstimmen. Ist die Ordnung der Polstelle gerade, so ist dies stets gegeben und der Grenzwert ist ${\displaystyle \infty }$ oder ${\displaystyle -\infty }$.

Bei einem Pol ungerader Ordnung kann man nur dann von einem Grenzwert sprechen, wenn ${\displaystyle +\infty =-\infty }$ gesetzt wird. Diese Einpunktkompaktifizierung erhält aber nicht die kleiner/gleich-Relation und wirkt deswegen zunächst unnatürlich. Die reellen Zahlen können aber in die komplexen Zahlen eingebettet werden und, da diese nicht angeordnet sind, ist es durchaus sinnvoll.

Beispiele

Die Funktion ${\displaystyle f(x)={\frac {1}{x^{2}}}}$ hat einen Pol 2. Ordnung bei ${\displaystyle x=0}$.

Die Funktion ${\displaystyle f(x)={\frac {1}{(x-2)^{3}}}}$ hat einen Pol 3. Ordnung bei ${\displaystyle x=2}$.

Die Funktion ${\displaystyle f(x)={\frac {x+2}{x^{3}+x^{2}-x-1}}={\frac {(x+2)}{(x+1)^{2}(x-1)}}}$ hat für ${\displaystyle x=-1}$ eine Polstelle der Ordnung 2 und für ${\displaystyle x=1}$ eine Polstelle 1. Ordnung.

Die Funktion ${\displaystyle f(x)={\frac {x^{2}+3x+2}{x^{3}+x^{2}-x-1}}={\frac {(x+2)(x+1)}{(x+1)^{2}(x-1)}}={\frac {(x+2)}{(x+1)(x-1)}}}$ hat für ${\displaystyle x=-1}$ und ${\displaystyle x=1}$ Polstellen der Ordnung 1.

Schwierigkeiten bei der Verallgemeinerung

Während es nach obigem Vorgehen keine Probleme bereitet, z. B. für die Tangensfunktion die Existenz und Ordnung der Polstellen anzugeben, wird es bei der Logarithmusfunktion für ${\displaystyle x=0}$ unmöglich. Generell bereitet jede glatte, aber nicht-analytische Funktion Schwierigkeiten. Eine Möglichkeit, damit umzugehen, bieten funktionentheoretische Mittel.

Komplexe Funktionen

Sei ${\displaystyle G\subset \mathbb {C} }$ ein Gebiet, ${\displaystyle D\subset G}$ eine diskrete Teilmenge und ${\displaystyle f\colon G\setminus D\to \mathbb {C} }$ eine holomorphe Funktion. Dann kann ${\displaystyle f}$ auf den Punkten von ${\displaystyle D}$ drei verschiedene Arten von isolierten Singularitäten haben.

Definition

Folgende Definition enthält die Pole reellwertiger rationaler Funktionen als Spezialfall. Sei ${\displaystyle a\in D}$. Falls es ein ${\displaystyle k\in \mathbb {N} _{0}}$ gibt, sodass ${\displaystyle \textstyle \lim _{z\to a}(z-a)^{k}\cdot f(z)}$ in ${\displaystyle \mathbb {C} }$ existiert, so kommt es zu folgenden Fällen:

• ${\displaystyle k=0}$: Dann ist ${\displaystyle f}$ auf ${\displaystyle a}$ holomorph fortsetzbar.
• ${\displaystyle k\geq 1}$ und ${\displaystyle k}$ kleinstmöglich gewählt, dass der Grenzwert existiert. Dann liegt ein Pol der Ordnung ${\displaystyle k}$ vor.

Existiert keine solche natürliche Zahl ${\displaystyle k}$, so hat ${\displaystyle f}$ eine wesentliche Singularität in ${\displaystyle a}$.

Aus dem riemannschen Hebbarkeitssatz folgt, dass der Grenzwert ${\displaystyle \textstyle \lim _{z\to a}(z-a)^{k}\cdot f(z)}$ schon dann existiert, wenn ${\displaystyle (z-a)^{k}\cdot f(z)}$ in einer Umgebung von ${\displaystyle a}$ beschränkt ist.

Eine weitere Charakterisierung von Polstellen ist folgende: ${\displaystyle f}$ hat in ${\displaystyle a}$ genau dann einen Pol der Ordnung ${\displaystyle k}$, wenn der Hauptteil der Laurent-Reihe auf einer in ${\displaystyle a}$ punktierten Kreisscheibe endlich ist und der kleinste Index eines nichtverschwindenden Koeffizienten der Laurent-Reihe gerade ${\displaystyle -k}$ ist.

Meromorphe Funktionen

→ Hauptartikel: Meromorphe Funktion

Komplexe Funktionen, die auf einem Gebiet holomorph sind und deren Singularitäten höchstens Pole sind, werden auch meromorph genannt. Wegen des Identitätssatzes kann die Polstellenmenge einer auf ${\displaystyle \mathbb {C} }$ meromorphen Funktion nur diskret sein. Damit liegen in jeder kompakten Teilmenge höchstens endlich viele Pole. Für die gesamte Ebene belegt der Satz von Mittag-Leffler die Existenz von Funktionen mit unendlich vielen Polstellen. Mit Hilfe der Ordnung der Pol- und Nullstellen einer meromorphen Funktion kann ein Divisor definiert werden.

Betrachtet man den kompaktifizierten Abschluss der komplexen Zahlen ${\displaystyle {\overline {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}}$ , so bilden meromorphe Funktionen ihre Polstellen auf ${\displaystyle \infty }$ ab. Lässt man ${\displaystyle {\overline {\mathbb {C} }}}$ auch im Definitionsbereich zu, so haben genau die Polynome ${\displaystyle k}$-ten Grades in ${\displaystyle \infty }$ eine Polstelle der Ordnung ${\displaystyle k}$. Allgemein sind meromorphe Funktionen ${\displaystyle \mathbb {C} \to \mathbb {C} }$ holomorph auf ${\displaystyle {\overline {\mathbb {C} }}}$ , wenn sie in ${\displaystyle \infty }$ höchstens einen Pol haben. Damit sind dies holomorphe Funktionen auf einer komplexen Mannigfaltigkeit, nämlich der riemannschen Zahlenkugel. Es lässt sich zeigen, dass jede holomorphe Funktion ${\displaystyle {\overline {\mathbb {C} }}\to {\overline {\mathbb {C} }}}$ global als Quotient zweier Polynome ausgedrückt werden kann und somit stets eine rationale Funktion ist.

Satz vom Null- und Polstellen zählenden Integral

→ Hauptartikel: Residuensatz

Sei ${\displaystyle f}$ eine auf einem Gebiet ${\displaystyle G\subset \mathbb {C} }$ meromorphe Funktion. Dann gilt für jede glatte, geschlossene, rektifizierbare Kurve ${\displaystyle \gamma \subset G}$, die weder Null- noch Polstellen von ${\displaystyle f}$ berührt und die eine Teilmenge ${\displaystyle H\subset G}$ berandet:

${\displaystyle {\frac {1}{2\pi i}}\int _{\gamma }{\frac {f'(z)}{f(z)}}dz=N_{f}-P_{f}}$.

Dabei sind ${\displaystyle N_{f}}$ und ${\displaystyle P_{f}}$ die Anzahl der Null- bzw. Polstellen inklusive ihrer Vielfachheiten, die in ${\displaystyle H}$ liegen. Insbesondere gilt für jede auf ${\displaystyle G={\overline {\mathbb {C} }}}$ meromorphe Funktion ${\displaystyle N_{f}=-P_{f}}$.

Beispiele

f(x) = 1/sin(x)

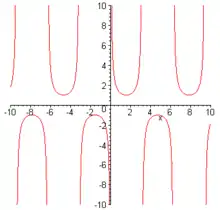
• Die Funktion ${\displaystyle f(x)={\tfrac {1}{x^{2}+1}}}$ hat zwei Pole 1. Ordnung bei ${\displaystyle x=\pm i}$.

• Der Kehrwert des Sinus ${\displaystyle f(x)={\tfrac {1}{\sin x}}}$ lässt sich analytisch fortsetzen auf ${\displaystyle \mathbb {C} }$ und hat einfache ungerade Pole bei allen ganzzahligen Vielfachen von π, da ${\displaystyle \textstyle \lim _{z\to n\pi }{\frac {z-n\pi }{\sin z}}=\pm 1}$.

• Die Tangensfunktion ${\displaystyle f(z)=\tan z}$ hat ungerade Pole bei allen ${\displaystyle z=(k+{\tfrac {1}{2}})\cdot \pi ,\;k\in \mathbb {Z} }$.

• Der komplexe Logarithmus ist eine Überlagerung und kann auf keinem Gebiet, das die Null enthält, stetig fortgesetzt werden. In ${\displaystyle 0}$ hat er keinen Pol, sondern einen Verzweigungspunkt.

Weiteres

• Das Pol-Nullstellen-Diagramm liefert mehrere Informationen über ein zu untersuchendes Signal.

Literatur

• Manfred Zimmermann (Hrsg.): Einführungsphase Mathematik. 5. Auflage. Transparent-Verlag, Berlin 1991, ISBN 3-927055-03-4.
• Georg Hoever: Höhere Mathematik kompakt. 2., korrigierte Auflage. Springer Verlag, Berlin/ Heidelberg 2014, ISBN 978-3-662-43994-4.

Weblinks

• Nullstellen, Polstellen, Lücken (abgerufen am 29. August 2016)
• Polstellen und hebbare Definitionslücken gebrochen rationaler Funktionen (abgerufen am 29. August 2016)
• Stabilität und Grenzstabilität (abgerufen am 29. August 2016)