Zeitgleichung

Als Zeitgleichung (ZG oder ZGL) wird die Differenz zwischen der wahren Sonnenzeit (wahre Ortszeit, WOZ) und der mittleren Sonnenzeit (mittlere Ortszeit, MOZ) bezeichnet:

ZG=WOZ-MOZ

Sonnenuhr mit Zeitgleichungs-Tabelle zur Korrektur der angezeigten wahren Sonnenzeit (wahre Ortszeit WOZ) auf mittlere Sonnenzeit (mittlere Ortszeit MOZ)[A 1]

Dieser Zeitunterschied ergibt sich, wenn die für einen bestimmten Ort ermittelte wahre Ortszeit – bei der die Sonne zu Mittag (12 Uhr WOZ) jeweils über der gleichen Stelle am Horizont steht, dem Südpunkt – verglichen wird mit einem konstruierten Zeitmaß (MOZ), das auf eine übers Jahr gemittelte Stellung der Sonne im Tageslauf Bezug nimmt. Die Unterschiede ergeben sich zum einen infolge Veränderungen der Bahngeschwindigkeit der Erde bei ihrem Umlauf (Revolution) um die Sonne auf der elliptischen Erdbahn sowie zum anderen aufgrund der Umdrehung (Rotation) der Erde um ihre Achse, die nicht senkrecht zur Bahnebene steht und bei der jährlichen Bewegung nahezu raumfest ausgerichtet bleibt:

aus der nahezu parallelen Verlagerung der geneigten Erdachse ergibt sich – mit ungefähr halbjährlicher Periode – ein periodischer Unterschied von etwa ± 10 Minuten,
aus der annähernd elliptischen Form der Erdbahn ergibt sich – mit ungefähr jährlicher Periode – ein periodischer Unterschied von etwa ± 7,5 Minuten.

Würden die Extrema beider Perioden zusammenfallen, ergäbe sich für die Zeitgleichung als Maximum +17,5 Minuten (+7,5 + 10) oder als Minimum −17,5 Minuten (−7,5 − 10). Derzeit liegen die jährlichen Extremwerte bei etwa +16 und etwa −14 Minuten.

Die Zeitgleichung ändert sich stetig um bis zu etwa 30 Sekunden in 24 Stunden. In üblichen Tabellenwerken wird der Wert der Zeitgleichung für jeden Tag des jeweiligen Jahres für den Zeitpunkt 12:00 UT angegeben. Für dazwischen liegende Zeitpunkte kann man interpolieren. Für viele Anwendungen kann es auch ausreichen, den angegebenen Wert für den ganzen Tag zu benutzen.

Die meisten Sonnenuhren zeigen die wahre Sonnenzeit an und gehen folglich gegenüber der mittleren Sonnenzeit zeitweise bis etwa 16 Minuten vor beziehungsweise bis etwa 14 Minuten nach.[1] Eine manchmal neben dem Zifferblatt angegebene Zeitgleichungstabelle oder ein -diagramm hilft dem Benutzer, die mittlere Zeit auszurechnen (oberes Bild). Oftmals wird in Analogie zur Mitteleuropäischen Zeit MEZ die wahre Sonnenzeit des 15. östlichen Längengrades angezeigt, indem die Bezifferung um die konstante Längendifferenz zwischen Standort und Bezugsmeridian, umgerechnet ins Stundenmaß, abgeändert ist. Man erhält von einer solchen Sonnenuhr die MEZ durch Korrektur mit dem Wert der Zeitgleichung und erspart sich die sonst noch nötige Reduktion von der örtlichen mittleren Sonnenzeit zur MEZ.

Das folgende Diagramm (unteres Bild) ist ein etwas mehr als ein Jahr langer Ausschnitt aus der prinzipiell stetig aus der Vergangenheit in die Zukunft fortlaufenden Zeitgleichung (rote Linie). Es gibt keinen exakt gleichen jährlichen Verlauf. Die jeweils vier Jahre auseinanderliegenden Werte (zum Beispiel die für 2011 im Diagramm und die künftigen für 2015) unterscheiden sich aber lediglich um Sekunden. Innerhalb der vierjährigen Schaltperiode decken sich die Jahresausschnitte infolge der kleinen Verschiebungen der kalendarischen Tagesskala (< ±1Tag) gegen das Sonnenjahr mit etwas größeren Abweichungen, die dennoch kleiner als ±1 Minute sind.

In astronomischen Jahrbüchern werden die Zeitgleichungswerte jährlich für die Tage des jeweiligen Jahres berechnet und sekundengenau angegeben. In ihnen können auch jüngste Erkenntnisse zum Einfluss der astronomischen Ursachen berücksichtigt sein.

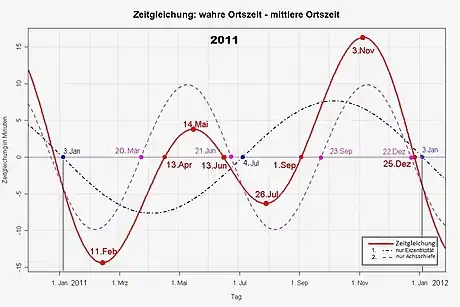
Zeitgleichung in Minuten, Ausschnitt für 2011 (erstes Jahr der Berechnung).
Zusätzlich sind die Beiträge der beiden Anteile zu sehen: 1. (strichpunktiert) nur Exzentrizität (Erdachse nicht schief, Periode 1 Jahr); 2. (gestrichelt) nur Achsschiefe (Erde auf Kreisbahn, Periode 1 Halbjahr).

Historisches

Die Zeitgleichung war schon den antiken Astronomen bekannt. Geminos von Rhodos erwähnt sie.[2] Im Almagest des Ptolemäus wurde sie recht genau und bündig angesprochen.[3] Bald nach Bekanntwerden der Keplerschen Gesetze hat John Flamsteed 1672 die quantitative Beschreibung eingeführt.[4][5]

In der älteren Literatur sind Minuend und Subtrahend vertauscht. Dieses Resultat mit umgekehrtem Vorzeichen wurde der früher im Alltag benutzten, auf einer Sonnenuhr angezeigten wahren Sonnenzeit hinzugefügt, um die mit der neu erfundenen Räderuhr dargestellte mittlere Sonnenzeit zu erhalten. Dieser Vorgang entspricht der alten Bedeutung von „Gleichung“ als „zuzufügende Korrektur“.[6] In französischen Jahrbüchern ist diese Konvention heute noch üblich.[7]

Heutzutage hat die mittlere Zeit, die man von (prinzipiell) stets gleichmäßig laufenden Uhren abliest, Priorität, und man folgert aus ihr die wahre Sonnenzeit. Die heutige Vorzeichenregelung wurde getroffen, um auch bei dieser Gewohnheit „zufügend korrigieren“ zu können.[A 2]

Siderischer Tag, Sonnentag und mittlere Sonne

Siderischer Tag und Sonnentag

Schematische Darstellung – auf der sich drehenden und mit gleichem Drehsinn in der Ekliptikebene die Sonne umlaufenden Erde dauert ein Sonnentag länger als ein Siderischer Tag:
von 1 nach 2 = ein Siderischer Tag
von 1 nach 3 = ein Sonnentag

Die Zeitspanne zwischen zwei Meridiandurchgängen der Sonne ist ein Sonnentag; er beträgt im Mittel 24 Stunden. Im Unterschied dazu wird die Zeitspanne zwischen zwei Meridiandurchgängen eines Fixsternes als Siderischer Tag bezeichnet. Dieser entspricht der Dauer für eine Drehung der Erde um sich selbst und beträgt im Mittel 23 Stunden 56 Minuten und 4 Sekunden. Der Unterschied von durchschnittlich 3 Minuten und 56 Sekunden zum Sonnentag ergibt sich durch die jährliche Bewegung der Erde auf ihrer Bahn um die Sonne. Von Tag zu Tag kommt die Erde auf der Erdbahn um nahezu einen Bogengrad voran (auf einen vollen Umlauf von 360 Grad entfallen rund 365 Sonnentage beziehungsweise rund 366 Siderische Tage). Da Umdrehung und Umlauf beide den gleichen Drehsinn haben, muss sich die Erde um ebenfalls knapp ein Grad über die volle Umdrehung hinaus weiterdrehen, bis die Sonne wieder durch den gleichen Meridian geht. Diese täglichen zusätzlichen Teildrehungen machen in einem Jahr genau eine ganze Umdrehung aus. Daher ist die Anzahl der auf den Meridiandurchgang der Sonne bezogenen Tage um 1 kleiner als die der siderisch bezogenen Tage.

Die Erdrotation ist sehr gleichmäßig, weshalb die Dauer eines Siderischen Tages nur sehr gering schwankt. Dagegen sind die Schwankungen in der Dauer von Sonnentagen erheblich größer, wegen der geneigten Rotationsachse der Erde und ihrer unterschiedlichen Bahngeschwindigkeit auf der elliptischen Bahn um die Sonne. Sonnentage können bis etwa 30 Sekunden länger oder bis etwa 20 Sekunden kürzer sein als ihr mittlerer Wert. Ihre Unterschiede vom Mittelwert können sich über Monate hinweg bis zu rund einer Viertelstunde aufsummieren, bevor sich der Effekt wieder umkehrt. Die am Sonnenstand abgelesene wahre Sonnenzeit (WOZ) vergeht somit ungleichmäßig. Ihre Abweichung von der gleichmäßig vergehenden, zum Beispiel von einer Räderuhr ablesbaren, mittleren Sonnenzeit (MOZ) ist die sogenannte Zeitgleichung.

Mittlere Sonne

Als der von der (scheinbaren) Bewegung der (wahren) Sonne „gemachte“ Sonnentag als ungleichmäßig lang erkannt wurde, der Sonnentag aber grundlegendes Zeitmaß bleiben sollte, wurde auf den formalen Gebrauch einer fiktiven sogenannten mittleren Sonne ausgewichen und mit der sogenannten mittleren Sonnenzeit ein gleichmäßiges Zeitmaß geschaffen. Die künstliche mittlere Sonne dieses Modells läuft gleichmäßig und nicht auf der Ekliptik, sondern auf dem Himmels-Äquator um und „macht“ dabei den mittleren Sonnentag.

Zwei Zeitgleichungsursachen, überlagert

Die Ursachen für die Zeitgleichung erkennt man leichter aus heliozentrischer Sicht, denn sie folgen aus den Bewegungen der Erde relativ zur ruhenden Sonne. Der Einfachheit halber wird gelegentlich weiterhin von „Sonnenzeit“ gesprochen, auch wenn es sich um Bewegungen der Erde, nicht um die der Sonne, in Abhängigkeit von der Zeit handelt.

Erste Ursache: Elliptizität der Erdbahn

Die Bahn der Erde um die Sonne ist eine Ellipse, in deren einem Brennpunkt die Sonne steht. Das zweite Keplersche Gesetz beschreibt die Veränderung der Bahngeschwindigkeit der Erde während eines Umlaufs. In der Umgebung des Perihels – des sonnennächsten Punkts – bewegt sich die Erde – von der Sonne gesehen – mit höherer Winkelgeschwindigkeit als im Mittel und legt während eines Tages einen größeren Winkel zurück, so dass sie eine etwas größere Zusatzdrehung machen muss, bis die Sonne wieder durch den Meridian geht. Das dauert länger als im Durchschnitt. In der Umgebung des Aphels – des sonnenfernsten Punkts – ist es umgekehrt.

In Perihel-Umgebung (Winterhalbjahr auf der Nordhalbkugel) vergeht die wahre Sonnenzeit wegen der größeren Erdgeschwindigkeit (und der dadurch nötigen größeren Zusatzdrehung) langsamer, in Aphel-Umgebung (Sommerhalbjahr auf der Nordhalbkugel) vergeht sie schneller als die gleichmäßige mittlere Sonnenzeit. Die Änderung der wahren Tageslänge zwischen zwei Tagen beträgt maximal etwa ±8 Sekunden.[8] Die Summierung dieser Änderungen ergibt innerhalb eines Jahres maximal etwa ±7½ Minuten Schwankung der wahren Sonnenzeit (sinus-ähnliche schwarze Linie in oben stehendem Diagramm (ohne Ekliptikschiefe), Nulldurchgänge im Perihel und im Aphel[A 3]).

Durch die Überlagerung der zweiten Ursache der Zeitgleichung werden die aus der ersten Ursache resultierenden Schwankungs-Werte verändert.

Zweite Ursache: parallele Verlagerung der geneigten Erdachse

Die Richtung der Erdachse, die die Ebene der Erdbahn schräg (im oben dargestellten Schema nicht beachtet) mit etwa 23,44° Abweichung von der Normale schneidet, ist relativ zu den Fixsternen nahezu unveränderlich. Von der Sonne aus betrachtet ändert die Erdachse täglich ihre Richtung, sie macht eine volle Taumelbewegung pro Jahr. Die tägliche Bahnfahrt der Erde ist eine Drehung (etwa 1°) um die Bahnachse (bzw. um die Sonne). Die dadurch erforderliche Zusatzdrehung der Erde erfolgt um ihre eigene Achse. Da beide Achsen nicht parallel sind, sind beide Drehungen nicht gleich groß.

An den Tag-und-Nacht-Gleichen schneiden sich die beiden Achsen von der Sonne aus gesehen unter dem Winkel ε ≈ 23,44°. Der Schnittwinkel ist jetzt am größten. Die Drehung der Erde um ihre Achse wirkt sich mit maximaler Verstärkung als Drehung um die zu ihrer Bahnebene (Ekliptik) rechtwinklige Achse aus. Folge ist, dass die Zusatzdrehung und die dafür erforderliche Zeit kleiner als im Mittel sind. Die wahre Sonnenzeit vergeht schneller als die mittlere Sonnenzeit.

An den Sonnenwenden decken sich beide Achsen scheinbar. Einer der beiden Erdpole ist aber der Sonne näher als der andere. Die tägliche 1°-Drehung der Erde um die Bahnachse bildet sich als Bogen auf einem ihrer beiden Wendekreise ab. Der zugehörende Bogen auf dem Erdäquator ist größer. Die erforderliche Zusatzdrehung der Erde um ihre Achse und die dafür erforderliche Zeit sind größer als im Mittel. Die wahre Sonnenzeit vergeht langsamer als die mittlere Sonnenzeit.

Wenn die erste Ursache der Zeitgleichung entfiele (fiktiver Grenzfall), betrüge die Änderung der wahren Tageslänge zwischen zwei Tagen maximal etwa ± 20 Sekunden.[9] Die Summierung dieser Änderungen ergibt innerhalb eines Jahres maximal etwa ± 10 Minuten halbjährliche Schwankung der wahren Sonnenzeit (sinus-ähnliche Magenta-farbene Linie in oben stehendem Diagramm: auf Kreisbahn; Start etwa zur Wintersonnenwende[A 4]).

Zeitgleichung, Überlagerung zweier Ursachen

Die Wirkungen der Elliptizität der Erdbahn und der parallelen Verlagerung der geneigten Erdachse resultieren zur Zeitgleichung. Die beiden sinus-ähnlichen Linien sind Annäherungen, und ihre relative Phasenlage ändert sich auch langsam im Laufe der Zeit. Letzteres verursacht im Wesentlichen die langsame Werte-Änderung der prinzipiell insgesamt vier Extremwerte der Zeitgleichung. Den absoluten Größtwert von etwa |17,5| min kann wegen des Periodenverhältnisses von 2 : 1 der beiden jeweils sinus-ähnlichen Linien nur einer der vier Extremwerte haben. Positiv/negativ gleiche Wertepaare sind möglich. Ihre beiden Werte können unmittelbar nacheinander (wie es annähernd zur Zeit der Fall ist) oder zeitlich versetzt auftreten (s. auch unten im Abschnitt Analemma).

Die Zeitgleichung hat gegenwärtig (2011) folgende Kennwerte (siehe rote Linie in obigem Diagramm):

Nullpunkte: 13. April, 13. Juni, 1. September und 25. Dezember,
Hauptextremwerte: 11. Februar (−14 min 14 s) und 3. November (+16 min 26 s) – ein annähernd gleiches Wertepaar.
Nebenextremwerte: am 14. Mai (+3 min 40 s) und am 26. Juli (−6 min 32 s) – ein weiteres annähernd gleiches Wertepaar.

Negative Zahlenwerte bedeuten: Die wahre Sonnenzeit läuft der mittleren Sonnenzeit beziehungsweise die wahre Sonne der mittleren Sonne nach.
Positive Zahlenwerte bedeuten: Die wahre Sonnenzeit läuft der mittleren Sonnenzeit beziehungsweise die wahre Sonne der mittleren Sonne voraus.

Berechnung

Zur Ermittlung eines Zeitgleichungswerts für einen gegebenen Zeitpunkt $t$ ist die Differenz WOZ – MOZ (s. o.) auf den Sonnenstand und den Stand einer fiktiven mittleren Sonne zurückzuführen. Die Rotation der Erde um ihre Polachse spielt dabei keine Rolle.

Modell der mittleren Sonnen

Zeitgleichung als Winkel
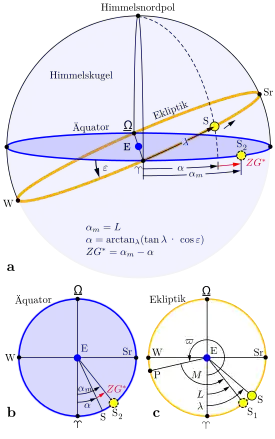
a Himmelskugel
b Äquatorialschnitt c Ekliptikalschnitt
Winkel

ZG^{*}

gespreizt
Die Punkte auf der Ekliptik bezeichnen geozentrische Projektionen der Sonne auf die Himmelskugel zu verschiedenen Zeitpunkten: ♈ und ♎ bei Frühlings- bzw. Herbstanfang (Frühlings- bzw. Herbstpunkt); Sr und W bei Sommer- bzw. Winteranfang. S: Anfang Mai. E: Erde. P: Perihel. Übrige Bezeichnungen s. Text

Zur Erläuterung der Zeitgleichung werden zwei fiktive mittlere Sonnen[10] herangezogen.(Abbildung rechts). Die erste mittlere Sonne $\mathrm {S} _{1}$ läuft gleichmäßig mit der mittleren Winkelgeschwindigkeit des Sonnenumlaufs in der Ekliptik um und durchläuft zusammen mit der wahren Sonne $\mathrm {S}$ das Perihel. Die zweite mittlere Sonne $\mathrm {S} _{2}$ läuft mit derselben Periode im Äquator um und passiert gleichzeitig mit $\mathrm {S} _{1}$ den Frühlingspunkt ♈. $\mathrm {S} _{2}$ ist die mittlere oder Vergleichssonne mit der Rektaszension $\alpha _{m}.$

Ausgehend von diesem Modell ergibt sich die Zeitgleichung zu

ZG{}^{*}=\alpha _{m}-\alpha ,

wobei $\alpha$ die Rektaszension der (wahren) Sonne bezeichnet. Der hochgestellte Stern weist darauf hin, dass $ZG^{*}$ als Winkel statt als Zeit angegeben ist. Wenn die wahre Sonne westlich der mittleren steht, ist WOZ > MOZ, aber $\alpha <\alpha _{m}$ . Daher ist die Reihenfolge von Minuend und Subtrahend gegenüber der anfänglichen Definition per Zeitunterschied umgedreht.

Im Tageslauf durchläuft die Sonne 360° in 24 Stunden oder 1° in 4 min. Damit gilt für die Zeitgleichung in Minuten

ZG=4\cdot ZG^{*}.

$ZG^{*}$ ist in Grad einzusetzen. Das Winkel- und das Zeitformat der Zeitgleichung sind übereinstimmende Versionen desselben Begriffs.

Rektaszension der wahren und der Vergleichssonne

**Bahnelemente des scheinbaren Sonnenumlaufs**
$e$	=	$\textstyle 0{,}016709-{\frac {0{,}000042}{36525}}\cdot t$
		numerische Exzentrizität
$\varepsilon$	=	$\textstyle 23+26/60+21/3600-{\frac {46{,}82/3600}{36525}}\cdot t$
		Schiefe der Ekliptik in Grad
$\varpi$	=	$\textstyle 282{,}9400+{\frac {1{,}7192}{36525}}\cdot t$
		Länge des Perihels in Grad
$L$	=	$\textstyle 280{,}4656+{\frac {36000{,}7690}{36525}}\cdot t$
		mittlere Länge in Grad
$t$	=	Zeit ab 1. Januar 2000 12:00 UTC in Tagen

Im Folgenden werden die Rektaszensionen $\alpha$ und $\alpha _{m}$ für den Zeitpunkt $t$ ermittelt. Die Rechnung basiert auf dem Kepler'schen Zweimassenmodell, wobei hier allerdings die Erde als Zentral- und die Sonne als Umlaufkörper aufgefasst wird. Das ist zulässig, weil der geozentrische Ortsvektor der Sonne dem heliozentrischen Ortsvektor der Erde genau entgegengesetzt ist (vgl. Sonnenbahn). Damit gilt der Kepler’sche Formelsatz auch für die scheinbare Bahn der Sonne[11] (s. a. Sonnenstand).

Zur Bestimmung der Rektaszension der Sonne $\alpha$ sind einige Elemente ihrer scheinbaren Bahn um die Erde nötig. Die rechts tabellierten Werte sind Montenbruck[12] entnommen. Montenbruck gibt die Bahnelemente[13] für die Erde an. Weil hier die Sonne der Umlaufkörper ist, sind die Längen $L$ und $\varpi$ in der Tabelle um 180° vergrößert.

Der vorgegebene Termin, für den die Zeitgleichung ausgerechnet werden soll, legt die Zeit $t$ fest, wie in der letzten Zeile der Tabelle angegeben. Damit kann die mittlere Anomalie der scheinbaren Sonne

M=L-\varpi

aus zwei Bahnelementen lt. Tabelle bestimmt werden. Die Länge der wahren Sonne in der Ekliptik

\lambda =L+C

ergibt sich aus einer Reihenentwicklung der Mittelpunktsgleichung[14]

C={\frac {180}{\pi }}\left[\left(2e-{\frac {e^{3}}{4}}\right)\sin M+{\frac {5}{4}}e^{2}\sin(2M)+{\frac {13}{12}}e^{3}\sin(3M)+\dots \right]

mit ausreichender Genauigkeit. Die Mittelpunktsgleichung $C=\lambda -L$ beschreibt die scheinbare Sonnenbewegung (Bahnellipse der Erde) mit gleichem Ergebnis wie die aus der Keplergleichung ermittelte Lösung.

Die Rektaszension der Sonne $\alpha$ hängt mit ihrer ekliptikalen Länge $\lambda$ über die Transformationsformel

\alpha =\arctan _{\lambda }(\tan \lambda \cdot \cos \varepsilon )

von ekliptikalen in äquatoriale Koordinaten zusammen (Schiefe $\varepsilon$ s. Tabelle). Der Index $\lambda$ bei arctan ruft den (Neben-)Wert der Arkustangensrelation auf, der $\lambda$ am nächsten liegt (s. Arcustangens mit Lageparameter).

Um die Bahn der zweiten mittleren Sonne $\mathrm {S} _{2}$ mit derjenigen der ersten in der von Schneider (s. o.) beschriebenen Weise zu synchronisieren, ist der mittleren Rektaszension $\alpha _{m}$ der Zeitverlauf des Sonnenbahnelements $L$ (vgl. Tabelle) zuzuweisen.[15] Mit

\alpha _{m}=L

liegen alle Größen zur Berechnung von $ZG^{*}$ und $ZG$ vor.

Resultat

Ausgehend von $ZG{}^{*}=\alpha _{m}-\alpha =L-\alpha$ führen die bisherigen Angaben zur zusammenfassenden Formel

ZG^{*}=L-\arctan _{\lambda }(\tan \lambda \cdot \cos \varepsilon ),\qquad (*)

die sich mit einem Tangens-Additionstheorem in

ZG^{*}=\arctan {\frac {\tan L-\tan \lambda \cdot \cos \varepsilon }{1+\tan L\cdot \tan \lambda \cdot \cos \varepsilon }}

umformen lässt.

Komponenten

Die Zeitgleichungsfunktion lässt sich gemäß

ZG^{*}=ZG_{\varepsilon =0}^{*}+ZG_{\varepsilon }^{*}

aus zwei Komponenten zusammensetzen[16]. Der linke Summand beziffert den Beitrag der Bahnexzentrizität $e$ („erste Usache“, s. o.) bei senkrecht auf der Ekliptik stehender Erdachse ( $\varepsilon =0$ ). Aus Gl. $(*)$ folgt dafür

ZG_{\varepsilon =0}^{*}=L-\lambda .

Dieser Teil verläuft sinusähnlich mit Jahresperiode. Die Werte sind gleich denen der negativen Mittelpunktsgleichung $C.$ . Die beiden Nullstellen fallen mit den Apsiden zusammen.
Der rechte Summand bezeichnet den Beitrag, der nach berücksichtigter Exzentrizität $e$ durch die Schiefe der Ekliptik $\varepsilon$ hinzukommt („zweite Usache“, s. o.). Er ergibt sich zu

ZG_{\varepsilon }^{*}=\lambda -\alpha

und verläuft ebenfalls sinusähnlich, aber mit zwei Perioden pro Jahr. Die vier Nullstellen fallen mit den Jahreszeitanfängen zusammen.

Geltungsdauer und Genauigkeit

Die Zeitgleichungsformel $(*)$ ist mit den tabellierten Konstanten mehrere Jahrhunderte vor und nach dem Jahr 2000 anwendbar. Die Werte weichen um weniger als 5 s von denen eines genauen Referenzmodells (z. B. VSOP) ab, das – anders als das Kepler-Modell – die Störkräfte der anderen Planeten und vor allem des Mondes berücksichtigt.

Zahlenbeispiel

Die Tabelle enthält die Werte in der Reihenfolge der Rechenschritte ohne Zwischenergebnisrundung. Die Himmelskugel-Graphik passt grob zum gewählten Zeitpunkt.

Rechnung für 1. Mai 2015 15:00 UTC
	$\textstyle t$	$\textstyle e$	$\textstyle \varepsilon$	$\textstyle \varpi$	$\textstyle L=\alpha _{m}$	$\textstyle M$	$\textstyle C$	$\textstyle \lambda$	$\textstyle \alpha$
Wert	5599,125 d	0,016703	23,437°	283.204°	5799,228°	5516,025°	1,704°	5800,932°	5798,508°
Hauptwert					39,228°	116,025 °		40,932°	38,508°
	$\textstyle ZG^{*}$	$\textstyle ZG$	$\textstyle ZG_{\varepsilon =0}^{*}$	$\textstyle ZG_{\varepsilon =0}$	$\textstyle ZG_{\varepsilon }^{*}$	$\textstyle ZG_{\varepsilon }$
Wert	0,720°	2,88 min	-1,704°	-6.82 min	2,424°	9.70 min

Ein präziser Vergleichswert[17] für $ZG$ beträgt 2,89 min.

Zeitgleichungswerte für die Passage ausgezeichneter Bahnpunkte

Die Berechnung von Zeitgleichungswerten für die Passage ausgezeichneter Bahnpunkte ist kürzer und einfacher. Es entfällt die aufwändige und nicht geschlossen durchführbare Bestimmung eines zu einer vorgegebenen Zeit gehörenden Bahnortes. Für diese Berechnung empfiehlt sich Anwendung der Kepler-Gleichung.

Sonnenauf- und -untergang zur Zeit der Sonnenwenden

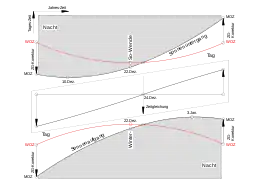
Sonnenauf- und -untergangszeiten im Dezember und am Anfang des Januars, schematisch

Dass der Sonnenuntergang schon mehrere Tage vor der Wintersonnenwende wieder später am Abend und der Sonnenaufgang erst mehrere Tage danach wieder früher am Morgen stattfindet, ist eine Folge der Zeitgleichung. In WOZ angegeben sind die Grenzen zwischen Nacht und Tag und zwischen Tag und Nacht zwar zueinander über die Datumsachse symmetrisch, nicht aber in MOZ. Nach der Korrektur der WOZ mittels Zeitgleichung zur MOZ ist der Tageskorridor (siehe nebenstehende Abbildung) verzerrt. Die Wendepunkte seiner Grenzlinien haben sich auf ein früheres Datum (Sonnenuntergang) beziehungsweise auf ein späteres Datum (Sonnenaufgang) verschoben.

Auf das Datum für den kürzesten lichten Tag im Jahr (Wintersonnenwende) hat das keinen merklichen Einfluss. Es bleibt etwa beim 22. Dezember (1-Tages-Variation infolge Schaltjahrzyklus).

Bei der Sommersonnenwende besteht der gleiche Effekt. Er ist weniger ausgeprägt als im Winter, weil die Steigung der Zeitgleichung als Funktion des Datums nur etwa ein Drittel so groß ist.

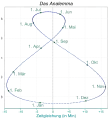
Analemma

Stundenschleife (Analemma) eines Mittagsweisers für MOZ,
darüber eine einfache Sonnenuhr (mit Stundengeraden für WOZ)

Stellt man die Abhängigkeit der Zeitgleichung von der Deklination der Sonne als Diagramm dar, entsteht eine Schleifenfigur, die als Analemma bezeichnet wird. Diese Schleife zeigt den wahren Stand der Sonne um 12 Uhr mittags mittlerer Ortszeit für die verschiedenen Jahreszeiten als Höhe über dem Himmelsäquator und als seitlichen Abstand vom Meridian. Dabei entsprechen in seitlicher Richtung vier Zeitminuten einem Grad im Winkelmaß. Die links gezeigten Figuren gelten nördlich des nördlichen Wendekreises mit der Blickrichtung nach Süden. In den Bildern links sind die Figuren gegenüber der Himmelsfigur in horizontaler Richtung ungefähr um den Faktor fünf bis sechs gedehnt. Rechts sieht man in einem historischen Mittagsweiser die zugehörige Schattenkurve (links/rechts unverzerrtes Analemma) auf einer vertikalen Wand markiert.

Die leichte Asymmetrie zwischen rechts und links rührt davon her, dass Perihel und Wintersonnenwende nicht auf denselben Tag fallen. Letzteres war zuletzt im Jahre 1246 der Fall (Tag der Wintersonnenwende etwa wie heute). Die innere Schnittstelle galt etwa für den 16. April und den 29. August (Gregorianischer Kalender rückwärts angewendet).

Im Jahre 6433 wird das Perihel den Tag des Frühlings-Äquinoktiums erreicht haben (Präzession). Die Zeitgleichung wird an den Tagen der Äquinoktien null und das Analemma eine zu diesem Punkt symmetrische Figur sein.[18]

Am häufigsten ist das Analemma als Stundenschleife auf Sonnenuhren zu sehen, die zur Anzeige der mittleren Sonnenzeit ausgelegt sind. Oftmals wird es allerdings in zwei Teile (ein Teil ähnlich einem S, der andere ähnlich einem Fragezeichen) aufgeteilt, um Verwechslungen beim Ablesen zu verhindern (für einen Deklinationswert gibt es zwei Punkte auf der ganzen Figur). Jedes der beiden Teile gilt etwa ein halbes Jahr lang. Solche Uhren haben zwei auswechselbare Zifferblätter.[1] Die Zifferblätter lassen sich leicht auf die am Aufstellort gültige Zonenzeit auslegen, zeigen also die „Normalzeit“ an.

Auch die jeden Tag zur gleichen mittleren Zeit fotografierte Sonne ergibt in der Summe ein am Himmel stehendes Analemma.[19]

Analemma, 20./21. Jahrhundert
Analemma, schematisch
Schwarz im Jahr 1246, Rot ca. 11.620
Analemma, schematisch
Rot im Jahr 6433, Schwarz ca. 16.810

Literatur

D. W. Hughes, B. D. Yallop, C. Y. Hohenkerk: The Equation of Time. In: Monthly Notices of the Royal Astronomical Society. Band 238, Juni 1989, ISSN 0035-8711, doi:10.1093/mnras/238.4.1529, bibcode:1989MNRAS.238.1529H, S. 1529–1535.
Bernd Loibl: Wann ist Mittag? In: Sterne und Weltraum. Spektrum der Wissenschaft, 8–9, 1996. S. 643–645.
Robert Weber. Zeitsysteme. In: Hermann Mucke (Hrsg.): Moderne astronomische Phänomenologie. 20. Sternfreunde-Seminar, 1992/93. Planetarium der Stadt Wien – Zeiss Planetarium der Stadt Wien – Zeiss Planetarium und Österreichischer Astronomischer Verein 1992, S. 55–102.

Weblinks

Commons: Zeitgleichung – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Zeitgleichung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Anmerkungen

Die Skala ist für MEZ ausgelegt, somit wird die für 15° Ost angezeigte wahre Sonnenzeit (wahre Ortszeit WOZ) auf mittlere Sonnenzeit (mittlere Ortszeit MOZ) für 15° Ost (gleich MEZ) korrigiert. Standort: 12° 22' Ost, Skalenverschiebung: etwa 10½ Minuten (entspricht dem Winkel zwischen Vertikaler und XII-Uhr-Linie).
In den meisten Fällen befindet sich der Beobachtungsort nicht auf dem Bezugslängengrad der gebrauchten Zonenzeit, die sich deshalb von seiner mittleren Ortszeit unterscheidet. Man muss letztere vorgängig ermitteln: Potsdam liegt z. B. 2° westlicher als 15° Ost, dem Bezugslängengrad der MEZ. Die mittlere Ortszeit ist hier 8 Minuten (4 Minuten / Längengraddifferenz) kleiner als die von der (Armband-)Uhr angezeigte MEZ.
Bei der Berechnung der Zeitgleichung in den ersten Näherungen wird die vom Mond periodisch verursachte Beschleunigung der Erde vernachlässigt. Man rechnet zum Beispiel für den Periheldurchgang gegenwärtig mit dem 3. oder 4. Januar (Unterschied innerhalb einer Vierjahres-Schaltperiode), was genau genommen nur für den gemeinsamen Massenmittelpunkt von Erde und Mond gilt. Erst bei angestrebter Genauigkeit im Sekundenbereich wird beachtet, dass der Massenmittelpunkt der Erde um den gemeinsamen Massenmittelpunkt näherungsweise auf einem Kreis mit einem Radius von etwa 4700 km umläuft, die Erde also in Bahnrichtung während einer Mondperiode zeitweise um bis zu 4700 km voraus oder zurück ist.
Die vier Jahreszeiten wären exakt gleich lang und deshalb die Kalenderdaten der Nulldurchgänge (Sonnenwenden und Tag-und-Nacht-Gleichen) bis etwa zwei Tage verschoben.

Einzelnachweise

Es existieren auch moderne Sonnenuhren, die für den Zeitausgleich konstruiert sind. Vgl. Siegfried Wetzel: Die Physik der Sonnenuhr. In: Deutsche Gesellschaft für Chronometrie (Hrsg.): Schriften des Historisch-wissenschaftlichen Fachkreises Freunde alter Uhren in der Deutschen Gesellschaft für Chronometrie. 1998, ISBN 3-923422-16-4, Abb. 16–18 (online, PDF).
O. Neugebauer: A History of Ancient Mathematical Astronomy. Berlin 1975.
R. Wolf: Handbuch der Astronomie. Amsterdam 1973
Flamsteed eröffnete seine Laufbahn mit einer wichtigen Abhandlung über die Bestimmung der Zeitgleichung. peter-hug.ch
Flamsteed J.: De inaequilitate dierum solarium dissertatio astronomica. London 1672 (online).
N. Dershowitz, E.M. Reingold: Calendrical Calculations. Cambridge University Press, 2008, ISBN 978-0-521-70238-6, S. 182.
J. Meeus: Astronomical Algorithms. Richmond 2000, S. 184.
Siegfried Wetzel Die Zeitgleichung, elementar behandelt - Private Homepage
Siegfried Wetzel Die Zeitgleichung, elementar behandelt - Private Homepage: Die angegebenen Werte folgen auf einfache Weise aus den Vorgaben 23,44° Abweichung der Erdachse von der Rechtwinkligkeit zur Bahnebene (Schiefe der Ekliptik) und 236 Sekunden, um die der mittlere Sonnentag länger als der Sterntag ist.
Manfred Schneider: Himmelsmechanik, Band II: Systemmodelle. BI-Wissenschaftsverlag, 1993, ISBN 3-411-15981-2, S. 507.
J. Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 1998/2009, Chapter 25: Solar Coordinates
O. Montenbruck: Grundlagen der Ephemeridenrechnung, Spektrum Akademischer Verlag Heidelberg, 7. Auflage 2005
Bahnelemente
Mittelpunktsgleichung, s. dort auch Anmerkung zur Herkunft der Mittelpunktsgleichung
Herleitung der Setzung $\alpha _{m}=L$ aus dem Schneider'schen Modell (s. Graphik Zeitgleichung als Winkel): Die Zeit $t_{F}$ der Frühlingspunktpassage von $\mathrm {S} _{1}$ in der Ekliptik folgt aus $L_{0}+{\dot {L}}t_{F}=0$ zu $t_{F}=-L_{0}/{\dot {L}}$ . $L_{0}$ und ${\dot {L}}$ sind die in der Tabelle Bahnelemente angegebenen Konstanten. Die Rektaszension von $\mathrm {S} _{2}$ im Äquator ist als lineare Gleichung $\alpha _{m}=\alpha _{m0}+{\dot {\alpha }}_{m}t$ anzusetzen. Da die Umlaufzeit beider mittlerer Sonnen gleich sein soll, gilt ${\dot {\alpha }}_{m}={\dot {L}}$ . Die beiden mittleren Sonnen gehen gemeinsam durch den Frühlingspunkt, was die Gleichung $\alpha _{m0}+{\dot {\alpha }}_{m}t_{F}=0$ nach sich zieht. Mit $t_{F}=-L_{0}/{\dot {L}}$ folgt daraus $\alpha _{m0}=L_{0}$ . Damit erfüllt die Setzung $\alpha _{m}=L$ die Merkmale des Zeitgleichungsmodells von Schneider.
M. Schneider: Himmelsmechanik, Band II: Systemmodelle, BI-Wissenschaftsverlag, 1993, S. 508, ISBN 3-411-15981-2
nach Multiyear Interactive Computer Almanac 1800 - 2050, U.S. Naval Observatory, Willmann-Bell 2005
Heinz Schilt: Zur Berechnung der mittleren Zeit für Sonnenuhren, Schriften der Freunde alter Uhren, 1990
Am Himmel in Griechenland fotografierte Analemmata perseus.gr

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Die Skala ist für MEZ ausgelegt, somit wird die für 15° Ost angezeigte wahre Sonnenzeit (wahre Ortszeit WOZ) auf mittlere Sonnenzeit (mittlere Ortszeit MOZ) für 15° Ost (gleich MEZ) korrigiert. Standort: 12° 22' Ost, Skalenverschiebung: etwa 10½ Minuten (entspricht dem Winkel zwischen Vertikaler und XII-Uhr-Linie).

[9] In den meisten Fällen befindet sich der Beobachtungsort nicht auf dem Bezugslängengrad der gebrauchten Zonenzeit, die sich deshalb von seiner mittleren Ortszeit unterscheidet. Man muss letztere vorgängig ermitteln: Potsdam liegt z. B. 2° westlicher als 15° Ost, dem Bezugslängengrad der MEZ. Die mittlere Ortszeit ist hier 8 Minuten (4 Minuten / Längengraddifferenz) kleiner als die von der (Armband-)Uhr angezeigte MEZ.

[11] Bei der Berechnung der Zeitgleichung in den ersten Näherungen wird die vom Mond periodisch verursachte Beschleunigung der Erde vernachlässigt. Man rechnet zum Beispiel für den Periheldurchgang gegenwärtig mit dem 3. oder 4. Januar (Unterschied innerhalb einer Vierjahres-Schaltperiode), was genau genommen nur für den gemeinsamen Massenmittelpunkt von Erde und Mond gilt. Erst bei angestrebter Genauigkeit im Sekundenbereich wird beachtet, dass der Massenmittelpunkt der Erde um den gemeinsamen Massenmittelpunkt näherungsweise auf einem Kreis mit einem Radius von etwa 4700 km umläuft, die Erde also in Bahnrichtung während einer Mondperiode zeitweise um bis zu 4700 km voraus oder zurück ist.

[13] Die vier Jahreszeiten wären exakt gleich lang und deshalb die Kalenderdaten der Nulldurchgänge (Sonnenwenden und Tag-und-Nacht-Gleichen) bis etwa zwei Tage verschoben.

[wetz-2] Es existieren auch moderne Sonnenuhren, die für den Zeitausgleich konstruiert sind. Vgl. Siegfried Wetzel: Die Physik der Sonnenuhr. In: Deutsche Gesellschaft für Chronometrie (Hrsg.): Schriften des Historisch-wissenschaftlichen Fachkreises Freunde alter Uhren in der Deutschen Gesellschaft für Chronometrie. 1998, ISBN 3-923422-16-4, Abb. 16–18 (online, PDF).

[3] O. Neugebauer: A History of Ancient Mathematical Astronomy. Berlin 1975.

[4] R. Wolf: Handbuch der Astronomie. Amsterdam 1973

[5] Flamsteed eröffnete seine Laufbahn mit einer wichtigen Abhandlung über die Bestimmung der Zeitgleichung. peter-hug.ch

[6] Flamsteed J.: De inaequilitate dierum solarium dissertatio astronomica. London 1672 (online).

[7] N. Dershowitz, E.M. Reingold: Calendrical Calculations. Cambridge University Press, 2008, ISBN 978-0-521-70238-6, S. 182.

[8] J. Meeus: Astronomical Algorithms. Richmond 2000, S. 184.

[Wetzel-10] Siegfried Wetzel Die Zeitgleichung, elementar behandelt - Private Homepage

[12] Siegfried Wetzel Die Zeitgleichung, elementar behandelt - Private Homepage: Die angegebenen Werte folgen auf einfache Weise aus den Vorgaben 23,44° Abweichung der Erdachse von der Rechtwinkligkeit zur Bahnebene (Schiefe der Ekliptik) und 236 Sekunden, um die der mittlere Sonnentag länger als der Sterntag ist.

[14] Manfred Schneider: Himmelsmechanik, Band II: Systemmodelle. BI-Wissenschaftsverlag, 1993, ISBN 3-411-15981-2, S. 507.

[15] J. Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 1998/2009, Chapter 25: Solar Coordinates

[16] O. Montenbruck: Grundlagen der Ephemeridenrechnung, Spektrum Akademischer Verlag Heidelberg, 7. Auflage 2005

[Bahnelemente-17] Bahnelemente

[Mittelpunktsgleichung-18] Mittelpunktsgleichung, s. dort auch Anmerkung zur Herkunft der Mittelpunktsgleichung

[alpha_m=L-19] Herleitung der Setzung $\alpha _{m}=L$ aus dem Schneider'schen Modell (s. Graphik Zeitgleichung als Winkel): Die Zeit $t_{F}$ der Frühlingspunktpassage von $\mathrm {S} _{1}$ in der Ekliptik folgt aus $L_{0}+{\dot {L}}t_{F}=0$ zu $t_{F}=-L_{0}/{\dot {L}}$ . $L_{0}$ und ${\dot {L}}$ sind die in der Tabelle Bahnelemente angegebenen Konstanten. Die Rektaszension von $\mathrm {S} _{2}$ im Äquator ist als lineare Gleichung $\alpha _{m}=\alpha _{m0}+{\dot {\alpha }}_{m}t$ anzusetzen. Da die Umlaufzeit beider mittlerer Sonnen gleich sein soll, gilt ${\dot {\alpha }}_{m}={\dot {L}}$ . Die beiden mittleren Sonnen gehen gemeinsam durch den Frühlingspunkt, was die Gleichung $\alpha _{m0}+{\dot {\alpha }}_{m}t_{F}=0$ nach sich zieht. Mit $t_{F}=-L_{0}/{\dot {L}}$ folgt daraus $\alpha _{m0}=L_{0}$ . Damit erfüllt die Setzung $\alpha _{m}=L$ die Merkmale des Zeitgleichungsmodells von Schneider.

[20] M. Schneider: Himmelsmechanik, Band II: Systemmodelle, BI-Wissenschaftsverlag, 1993, S. 508, ISBN 3-411-15981-2

[21] Multiyear Interactive Computer Almanac 1800 - 2050, U.S. Naval Observatory, Willmann-Bell 2005

[Schilt-22] Heinz Schilt: Zur Berechnung der mittleren Zeit für Sonnenuhren, Schriften der Freunde alter Uhren, 1990

[23] Am Himmel in Griechenland fotografierte Analemmata perseus.gr