Analemma
Der Begriff Analemma (griechisch ‚Umschreibung‘, ‚etwaige Annahme‘, ‚Vorschrift‘ für den Sockel einer Sonnenuhr) wird am häufigsten für die Figur gebraucht, die der Sonnenstand bei konstanter mittlerer Ortszeit erzeugt. Diese Figur entsteht zum Beispiel durch Fotos der Sonne, die man täglich zur selben mittleren Ortszeit (das heißt auch: zur selben Zonenzeit am selben Ort) über ein Jahr macht. Wenn man nach Ablauf eines Jahres alle diese Sonnenbilder in einer Fotomontage überlagert, erkennt man eine langgestreckte Acht (siehe Abbildung): das Analemma.

In der Gnomonik, der Lehre von den Sonnenuhren, ist das Analemma eine von Vitruv angegebene Vorschrift zur Konstruktion von Sonnenuhren.
Die Sonnenpositionen als Analemma
Die zum Analemma führende scheinbare Schwankung der Sonne ist eine Folge zweier Bewegungen der Erde:
- Die Bahn der Erde ist elliptisch
- die Abweichung der scheinbaren Bahnebene der Sonne, auch Ekliptik genannt, vom Himmelsäquator (Projektion des Äquators auf den Himmel) beträgt ca. 23,5°.
Wäre die Bahn der Erde ein exakter Kreis und stünde die Erdachse senkrecht auf der Bahnebene, dann befände sich die Sonne täglich im selben Moment einer gleichmäßig ablaufenden Zeit stets am selben Punkt am Himmel (auch nicht verschieden hoch, denn dann gäbe es auch keine Jahreszeiten).
Durch die beiden beschriebenen Abweichungen weicht die Sonne jedoch während eines Jahres von o. g. Punkt ab und wandert einmal durch eine Figur mit der Form einer „8“, das Analemma.
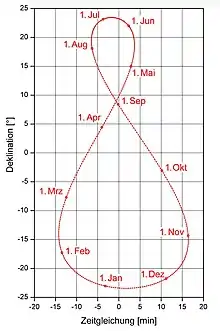
Die oben stehende Fotomontage zeigt die übers Jahr verschiedenen Sonnenstände um ca. 9 Uhr MEZ auf etwa dem 8. östlichen Längengrad und etwa dem 49. nördlichen Breitengrad, wobei die Sonne den unteren, breiteren Teil der Doppelschleife („8“) von Anfang September bis Mitte April im Uhrzeigersinn, den oberen, schmaleren Teil von Mitte April bis Anfang September entgegengesetzt durchläuft.
Die Abweichung von der eingezeichneten Hilfsgeraden ist das mit Hilfe der Zeitgleichung ausgedrückte Vor- beziehungsweise Nachgehen der wahren Sonnenzeit (wahre Ortszeit (WOZ)) von der künstlichen mittleren Sonnenzeit („mechanische Zeit“, mittlere Ortszeit (MOZ)). Der nebenstehenden Zeitgleichungsgraph ist im Vergleich zur oben stehenden Fotomontage in der Breite gestreckt, das Analemma in ihm nur schematisch.
Die Analemma-Figur bekam erst durch die Erfindung und den Gebrauch der prinzipiell gleichförmig laufenden mechanischen Uhr am Ende des Mittelalters allgemeine Bedeutung. Im Altertum war die scheinbare Bewegung der Sonne selbst allgemein benutzter Zeitmaßstab gewesen; ihr leicht ungleichförmiger Lauf wurde hingenommen bzw. war der Allgemeinheit unbekannt.
Das Analemma auf Sonnenuhren

Bei Sonnenuhren mit Punktanzeige ist die mittlere Ortszeit (MOZ) auf analemmaförmigen Stundenmarkierungen ablesbar. Auf der abgebildeten Wandsonnenuhr wird dabei nicht der Stab-Schatten auf den Stundenlinien, sondern der Punkt-Schatten (von der Kugel an der Stabspitze herrührend) auf den analemmaförmigen Stundenmarkierungen abgelesen.
Das Analemma des Vitruv
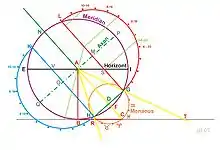
Im neunten seiner Zehn Bücher über die Architektur deutet Vitruv an, wie Sonnenuhren mithilfe einer Figur, die er Analemma nennt, konstruiert werden können. Er beschreibt, wie das Analemma allein bei Verwendung von Lineal und Zirkel zu zeichnen ist. Sein Beispiel gilt für Rom, er beginnt mit dem Verhältnis Schattenlänge zu Gnomonhöhe, wie es zu den Äquinoktien dort gültig ist. Die Gnomonspitze befindet sich im Zentrum A des Kreises, welcher den Meridian des Standortes darstellt. Aus dem Tangens der geografischen Breite von Rom, d. h. aus dem äquinoktialen Längenverhältnis Schatten zu Gnomon (8:9; C-B:A-B) lässt sich der Äquator und damit der Verlauf des Sonnenstrahls N-A-C zum Sonnenhöchststand am Mittag auftragen. Parallele Sekanten L-G und K-H zum Äquator im Abstand von 1/15 Kreisumfang approximieren die jeweiligen Bahnebenen der Sonne zu den Solstitien (Deklination der Sonne ±24°). Zur Wintersonnenwende wird die Sonne von K über A nach T projiziert. Zur Sommersonnenwende wird sie von L über A nach R abgebildet. In der gewählten Ansicht bewegt sich die Sonne auf diesen Solstitien-Sekanten zwischen Horizont E-I und den Mittagspunkten L und K einmal am Tag auf und ab. Somit sind die Schnittpunkte S und V dieser Bahnen mit dem Horizont die Konstellationen bei Sonnenaufgang und -untergang. Die zugehörige Zeit zur Tagesposition der Sonne kann ermittelt werden, wenn um die jeweilige Sekante der Sonnenbahn ein (Halb-)Kreis geschlagen wird, der in Stundenwinkel zu je 15° unterteilt wird. Die Unterteilung wird von Vitruv bereits nicht mehr beschrieben. In nebenstehender Abbildung ist die Zeitablesung für den Sonnenauf- und -untergang am Tag der Sommersonnenwende durch die Linie S – SA-SU dargestellt. Für den Deklinations-Bereich zwischen Sommer- und Wintersonnenwende kann der von Vitruv beschriebene Menaeus, der Monats- oder Tierkreis unterteilt werden. Auf diesem wird die dem gewünschten Kalendertag eines Monats entsprechende Position aufgetragen und durch diesen Punkt eine Parallele zum Äquator gezogen. Das ergibt die Sekante der Sonnenbahn dieses Tages. Ihr oberer Schnittpunkt mit dem Meridiankreis ergibt den Projektionsstrahl für die Mittagssonne. Um die Position der Sonne während der Tagesstunden ermitteln zu können, wird wieder ein Halbkreis mit entsprechender Stundenteilung um diese Sekante geschlagen.
Siehe auch
Literatur
- Georg Kauffmann: Analemma. In: Paulys Realencyclopädie der classischen Altertumswissenschaft (RE). Band I,2, Stuttgart 1894, Sp. 2052–2055.