Zahlenkreis

Der Zahlenkreis ist ein Begriff aus der maschinellen Datenverarbeitung. Er ist insbesondere hilfreich bei den endlichen Zahlensystemen, wie sie in Rechenwerken erforderlich sind. In diesen steht nur eine begrenzte Anzahl von Stellen zur Verfügung. Dies muss beim Rechnen sorgfältig berücksichtigt werden, um Fehler durch Überschreitung einer Begrenzung zu vermeiden. Mathematisch gesehen behandelt der Zahlenkreis eine Restklasse.

Grundlage

Bei der in Europa in Alltag und Wissenschaft üblichen Schreibweise von Zahlen wird eine Zahl in einem Stellenwertsystem dargestellt durch Ziffern, Vorzeichen und Trennzeichen (wie Komma, Leerzeichen). Eine Ziffer steht für eine Zahl aus einem beschränkten Vorrat. Durch eine Anordnung aus mehreren Ziffern entsteht ein unbeschränkter Vorrat an Zahlen. Jeder Platz in dieser Anordnung, den eine Ziffer einnimmt oder einnehmen soll, ist eine Stelle.[1] Jede Ziffer ist je nach der Stelle unterschiedlich zu bewerten („Einerstelle“, „Zehnerstelle“, …).

Das Stellenwertsystem enthält $b$ Ziffern, denen in der Regel die Werte der natürlichen Zahlen von $0$ bis $b-1$ zugeordnet werden.[1] Wird die Einerstelle, die den Stellenwert 1 hat, mit $i=0$ nummeriert, so hat die $i$ -te Stelle den Stellenwert $b^{i}$ .

Unter den vielen Stellenwertsystemen sind vorzugsweise das vertraute Dezimalsystem mit $b=10$ gebräuchlich und in der Digitaltechnik das Dualsystem mit $b=2$ oder das Sedezimalsystem[2] mit $b=16$ , das jeweils vier Stellen des Dualsystems zu einer Stelle zusammenfasst.

Unbeschränkter Zahlenvorrat

Das Stellenwertsystem entwickelt sich auf folgende Weise: Durch den Rechenschritt „Addition einer Eins“ wird auf der Einerstelle statt der vorhandenen Ziffer die Ziffer mit dem nächsthöheren Wert geschrieben. Steht da bereits die Ziffer mit dem höchsten Wert, wird an ihrer Stelle eine Null geschrieben und der Rechenschritt wird auf der nächst höherwertigen Stelle ausgeführt. Gibt es keine höherwertige Stelle, so wird vor die Ziffernfolge eine Null gesetzt und damit den Rechenschritt durchgeführt. Das System ist für weiter links stehende höherwertige Stellen unbeschränkt. Vor eine Zahl können beliebig viele Nullen geschrieben werden, was ihren Wert nicht ändert und normalerweise unterbleibt.

Bei negativen Zahlen wird ein Vorzeichen links vor die Ziffernfolge gesetzt. Diese steht dann für den Betrag der Zahl.

Zahlengerade mit der nach beiden Seiten unbegrenzten Anordnung der vorzeichenbehafteten (reellen) Zahlen

Die Unbegrenztheit des Zahlenvorrats wird veranschaulicht an der Unbegrenztheit einer Zahlengeraden.

Beschränkter Zahlenvorrat

Bei beschränktem Platz für Stellen, wie im Rechenwerk eines Mikroprozessors, ist die Verwendung eines unbeschränkten Zahlensystems nicht möglich. Bei Zahlen aus einem begrenzten Zahlenvorrat werden alle Stellen geschrieben, auch die mit führenden Nullen. Entsprechend der Anwendung bei Digitalrechnern befasst sich die Beschreibung hier nur mit Dualzahlen. Mit zwei Ziffern sind die Zahlen 000…000 bis 111…111 möglich mit der durch die Auslegung des Rechenwerkes festgelegten Anzahl von Stellen.

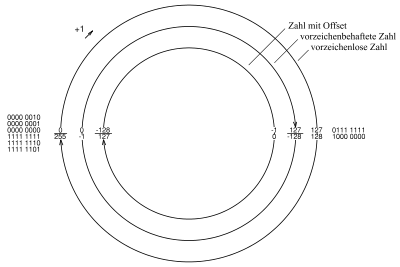
Zahlenkreis mit achtstelligen Dualzahlen und unterschiedlichen Dezimalzahl-Zuordnungen. Ein waagerechter Strich markiert die Grenzen des Zahlenbereiches.

Mit $n$ Stellen lassen sich $2^{n}$ natürliche Zahlen von $0$ bis $2^{n}-1$ darstellen. Der Rechenschritt „Addition einer Eins“ wird ausgeführt wie bei unbeschränktem Zahlenvorrat außer bei der Dualzahl 111…111, bei der es keinen Übertrag auf eine höherwertige Stelle gibt, so dass die Addition auf die Zahl 000…000 zurückführt. Dieses wird veranschaulicht an einem Zahlenkreis.[3][4][5]

Zur Darstellung negativer Zahlen aus dem Zahlenbereich $-2^{n-1}$ bis $2^{n-1}-1$ ist im Dualsystem das Zweierkomplement üblich, siehe auch Integer (Datentyp). Dadurch bleibt die Verarbeitung im Rechenwerk einfach, denn der Rechenschritt „Addition einer Eins“ bleibt in seiner Ausführung unverändert. Allerdings ist das Zweierkomplement für eine negative Zahl nicht wie in einem Stellenwertsystem aufgebaut.

Ferner ist zur Darstellung von $2^{n}$ vorzeichenbehafteten Zahlen ein Offset (Nullpunktversatz) im Gebrauch. Zur kleinsten (am weitesten negativen) Zahl gehört dann die (konventionell kleinste) Dualzahl 000…000, zur größten Zahl gehört 111…111, und die bei symmetrischem Zahlenbereich unmittelbar oberhalb der Mitte liegende Null gehört zur Dualzahl unmittelbar oberhalb der Mitte, zu 100…000. Der Rechenschritt „Addition einer Eins“ läuft auch hier wie beim Stellenwertsystem, aber keine der Zahlen ist wie in einem Stellenwertsystem aufgebaut.

Wird bei einer Addition oder Subtraktion eine Grenze des Zahlenbereichs überschritten, so entsteht ein fehlerhaftes Ergebnis, das aber vom Rechenwerk durch seine Statusbits gekennzeichnet wird.

Einzelnachweise

DIN 1333, Zahlenangaben, 1992, Kap. 10.1
DIN 1333, Kap. 8
Erich Leonhardt: Grundlagen der Digitaltechnik. Carl Hanser, 1984, Seite 147 ff
Erwin Samal, Wilhelm Becker: Grundriss der praktischen Regelungstechnik. Oldenbourg, 2004, Seite 507
Axel Böttcher, Franz Kneißl: Informatik für Ingenieure: Grundlagen und Programmierung in C. Oldenbourg, 2012, Seite 29 ff

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[D1333-1] DIN 1333, Zahlenangaben, 1992, Kap. 10.1

[2] DIN 1333, Kap. 8

[3] Erich Leonhardt: Grundlagen der Digitaltechnik. Carl Hanser, 1984, Seite 147 ff

[4] Erwin Samal, Wilhelm Becker: Grundriss der praktischen Regelungstechnik. Oldenbourg, 2004, Seite 507

[5] Axel Böttcher, Franz Kneißl: Informatik für Ingenieure: Grundlagen und Programmierung in C. Oldenbourg, 2012, Seite 29 ff