Zahlensystem
Ein Zahlensystem oder Ziffernsystem (seltener auch Zahlsystem genannt) legt fest mit welchen Ziffern eine Zahl dargestellt wird. Zahlen können mit einer eigenen Schrift dargestellt werden, wie arabischen Ziffern, oder verwenden normale Buchstaben, wie römische Ziffern. Eine moderne Zahlschrift enthält zusätzliche Zahlzeichen und Konventionen. Es gibt +, -, Komma, Tausendertrennzeichen, Bruchstrich, Potenz um nur einige zu nennen. Ein Ziffernsystem enthält meist auch Zahlworte wie "eins", "acht", "hundert", "dutzend".
Die moderne Forschung unterscheidet vor allem drei Ziffernsysteme nach den Regeln, wie die Ziffern angeordnet werden, bzw. wie zusammengezählt wird. Am bekanntesten ist das Stellenwertsystem, oder Positionssystem. Der Wert einer Ziffer ändert abhängig an welcher Stelle sie steht. Wenn die Eins an der zweiten Stelle steht, wie bei 10, dann hat sie den Wert zehn, wenn sie an der dritten Stelle steht, wie bei 100, dann hat sie den Wert hundert. Bei einem Additionssystem ist der Wert einer Ziffer immer gleich. 15 Striche in einer Strichliste, oder römisch XV haben den Wert von fünfzehn. Ein Hybridsystem ist ähnlich dem schriftlichen Deutsch. Anstatt 3'000'000 schreibt man 3 Millionen. Es wird für jede Ziffer zusätzlich angeben mit was man die Ziffer mal rechnet. Im traditionellen japanischen Ziffernsystem schreibt man 三万六十 drei mal zehntausend und 6 mal 10 für 30'060, der Multiplikator in grün.
Die bekanntesten positionellen Systeme werden mit speziellen Namen bezeichnet nach Anzahl der Ziffern. Das Zehnersystem oder Stellenwertsystem zur Basis 10 hat 10 Ziffern, 0 bis 9. Es heißt auch Dezimalsystem. Das 2er-System heißt Binärsystem, das 16er-System Hexadezimalsystem, das 12er auch Duodezimalsystem, das babylonische 60er-System heißt auch Sexagesimalsystem.[1]
Additionssysteme
In einem Additionssystem wird eine Zahl als Summe der Werte ihrer Ziffern dargestellt. Dabei verändert die Position einer Ziffer ihren Wert nicht. Ein Beispiel ist das Strichsystem (Unärsystem). Es bietet sich an, wenn etwas schriftlich mitgezählt werden soll (wie zum Beispiel die Getränke auf einem Bierdeckel). Hierbei wird die Zahl durch Striche dargestellt. Dies ist vermutlich eines der ältesten Zählsysteme überhaupt. Das Unärsystem wird bei der Darstellung größerer Zahlen sehr schnell unübersichtlich. Deshalb ist es meist üblich, die Zahlen in Blöcke zusammenzufassen, indem man etwa jeden fünften Strich quer über die vier vorangegangenen Einzelstriche legt. Obwohl es aus diesem Grund nicht geeignet ist, große Zahlen darzustellen, wird es im Alltag dennoch in manchen Situationen verwendet. Eine Addition um einen Zahlenwert ist einfach durch das Hinzufügen eines Striches möglich. Herkömmliche Systeme lassen eine so einfache und schnelle Erweiterung im Allgemeinen nicht zu. Das römische Ziffernssystem ist bereits etwas komplizierter. Buchstaben werden für 5er und 10er Zahlen verwendet, wie V für fünfzig. Es gibt auch spezielle Regeln nach der Position der Zeichen zueinander. XI ist elf, IX ist neun. Der Wert der Ziffern verändert sich jedoch nicht, ein I ist immer eine Eins.
Hybridsysteme
Hierbei wird eine Grundziffer einem Zeichen vorangestellt, das eine Potenz der Basis wiedergibt; die Werte beider werden miteinander multipliziert. In den europäischen Zahlensystemen kamen solche Hybridsysteme so gut wie nicht vor, wohl aber, schon seit Beginn des zweiten Jahrtausends v. Chr., in Mesopotamien, später auch in China und im Nahen Osten allgemein. Sowohl aus Äthiopien als auch aus Südindien und Sri Lanka sowie der Maya-Kultur sind solche hybriden Zahlensysteme bekannt.
Beispiele im japanisch-chinesischen Zahlensystem:
23: 二十三 (2 × 10 + 3) 30.000: 三万 (3 × 10.000)
Stellenwertsysteme
Aufbau
Im Alltag und in der Wissenschaft wird eine Zahl üblicherweise durch Ziffern (0, 1, 2, …, 9, die allein die ersten zehn der natürlichen Zahlen darstellen, und Buchstaben) und weitere Zahlenzeichen wie Vorzeichen (plus, minus) und Trennzeichen (Komma, Leerzeichen) dargestellt. Die Anzahl der verwendeten Ziffern wird „Basis des Stellenwertsystems“ genannt. Die gängigsten Basen sind 2 (beim Dualsystem), 8 (beim Oktalsystem), 10 (beim im Alltag gebrauchten Dezimalsystem) oder 16 (beim in der Datenverarbeitung wichtigen Hexadezimalsystem).
Die Ziffern haben eine durch Konvention festgelegte Reihenfolge ihres Wertes. Beim Hochzählen (das entspricht der Addition einer Eins) wird in dieser Reihenfolge zur nächsten Ziffer übergegangen. Bei der Addition einer Eins auf die höchstwertigste Ziffer wird auf die niederwertigste Ziffer übergegangen, und auf der nächsthöheren Stelle wird eine Eins addiert.
Dazu werden die Ziffern je nach ihrer Stelle unterschiedlich bewertet, wobei der Stellenwert eine Potenz der Basis ist (zum Beispiel „Einerstelle“, „Zehnerstelle“, „Hunderterstelle“, …). Die Stelle mit der niedrigsten Bewertung steht dabei ganz rechts. Die Berechnung des Zahlenwertes erfolgt dann durch Multiplikation der einzelnen Ziffernwerte mit den zugehörigen Stellenwerten und der Addition dieser Produkte.[2]
Auf diese Weise lässt sich in einem Stellenwertsystem jede natürliche Zahl darstellen. Für die Erweiterung auf negative Zahlen wird ein Vorzeichen links vor die Ziffernfolge gesetzt, mit dem angegeben wird, ob eine Zahl positiv oder negativ ist. Durch die Verwendung negativer Exponenten lassen sich in einem Stellenwertsystem auch rationale Zahlen schreiben, wobei der Übergang von nichtnegativen zu negativen Exponenten durch ein Trennzeichen in der Zahldarstellung markiert wird, beispielsweise ein Komma oder einen Punkt.
Darstellungsbereich
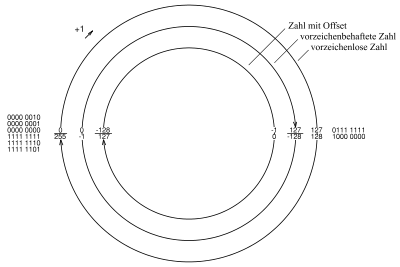
Die Menge der darstellbaren Zahlen lässt sich bei einer unbeschränkten Anzahl von Stellen an einer Zahlengeraden veranschaulichen. Steht nur eine beschränkte Anzahl von Stellen zur Verfügung, wird das an einem Zahlenkreis veranschaulicht. Bei dieser Beschränkung kann eine Addition oder Subtraktion von Zahlen aus dem Bereich der darstellbaren Zahlen herausführen.
Literatur
- Georges Ifrah: Universalgeschichte der Zahlen. 2. Auflage. Campus-Verlag, Frankfurt/Main 1987, ISBN 3-593-33666-9.
- John D. Barrow: Warum die Welt mathematisch ist. Campus-Verlag, Frankfurt/Main 1993, ISBN 3-593-34956-6.
- Guido Walz (Hrsg.): Lexikon der Mathematik. Band 5: Sed bis Zyl. 2. Auflage. Springer, Mannheim 2017, S. 442 f. (Zahlsystem).
Weblinks
- Online-Umrechner für verschiedene Zahlensysteme (JavaScript)
- Zahlen in beliebige Zahlensysteme umrechnen
- Online-Tool zum gleichzeitigen Konvertieren der Zahlensysteme (PHP)
- Es werde Zahl! Artikel zur Geschichte der Zahlensysteme mit Tabellen von ägyptischen Zahlhieroglyphen, hieratischen Zahlen und Keilschriftzahlen.
Einzelnachweise
- Scriptum Elementare Zahlentheorie, W.Hofmann, Uni Bielefeld, zugegriffen 2022-02-07.
- Axel Böttcher, Franz Kneißl: Informatik für Ingenieure: Grundlagen und Programmierung in C. Oldenbourg 2012.