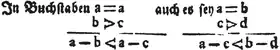Vergleichszeichen

Vergleichszeichen sind die in der mathematischen Notation üblichen Zeichen für die Darstellung der Größenverhältnisse zweier Zahlen oder Terme. Die wichtigsten Vergleichszeichen sind das Gleichheitszeichen (=) sowie das Größer-als-Zeichen (>) und das Kleiner-als-Zeichen (<). Vergleichszeichen können vielfältig kombiniert werden, etwa mit einer Tilde für die Äquivalenz. Durchgestrichene Varianten stehen für die Negation des ursprünglichen Verhältnisses. Viele der Kombinationen fallen in den meisten Anwendungen mit der Bedeutung anderer Zeichen zusammen.

< >
Mathematische Zeichen
Arithmetik
Pluszeichen	+
Minuszeichen	−, ⁒
Malzeichen	⋅, ×
Geteiltzeichen	:, ÷, /
Plusminuszeichen	±, ∓
Vergleichszeichen	<, ≤, =, ≥, >
Wurzelzeichen	√
Prozentzeichen	%
Analysis
Summenzeichen	Σ
Produktzeichen	Π
Differenzzeichen, Nabla	∆, ∇
Prime	′
Partielles Differential	∂
Integralzeichen	∫
Verkettungszeichen	∘
Unendlichzeichen	∞
Geometrie
Winkelzeichen	∠, ∡, ∢, ∟
Senkrecht, Parallel	⊥, ∥
Dreieck, Viereck	△, □
Durchmesserzeichen	⌀
Mengenlehre
Vereinigung, Schnitt	∪, ∩
Differenz, Komplement	∖, ∁
Elementzeichen	∈
Teilmenge, Obermenge	⊂, ⊆, ⊇, ⊃
Leere Menge	∅
Logik
Folgepfeil	⇒, ⇔, ⇐
Allquantor	∀
Existenzquantor	∃
Konjunktion, Disjunktion	∧, ∨
Negationszeichen	¬

Typografie und Aussehen

Winkelklammern, Vergleichszeichen und einfache Guillemets (halbe Spitzzeichen) in den Schriftarten Cambria, DejaVu Serif, Andron Mega Corpus, Andika und Everson Mono

Das Kleiner-als-Zeichen und das Größer-als-Zeichen bestehen aus einem in der Mitte abgeknickten Strich mit geraden Schenkeln, wobei der Knickwinkel regelmäßig spitz (also kleiner als ein rechter Winkel) ist. Die Endpunkte liegen senkrecht übereinander, sodass die Schenkel gleich lang sind; dies wird auch meistens in der Kursivschrift beibehalten. Die Höhe und Höhenlage der Zeichen entsprechen regelmäßig denen des Pluszeichens. Sie sind damit in den meisten Schriftart deutlich größer als Guillemets (Spitzzeichen) und andererseits deutlich kleiner als Winkelklammern. Letztere unterscheiden sich auch durch einen deutlich offeneren Winkel an der Knickstelle, zumeist deutlich größer als ein rechter Winkel.

Geschichte

Vergleichszeichen in einem Druck von 1631[1]

Kleiner-als- und Größer-als-Zeichen mit Serifen in einem Druck von 1802[2]

Die Zeichen > und < wurden von dem englischen Mathematiker Thomas Harriot 1631 in seinem Werk Artis Analyticae Praxis eingeführt. Das Zeichen ≥ wurde erstmals von dem französischen Mathematiker Pierre Bouguer im Jahr 1734 verwendet.[3]

Verwendung

Mathematik

In der Mathematik werden Vergleichszeichen (vom Gleichheitszeichen abgesehen) genutzt, um Ungleichungen zu bilden. In der elementaren Mathematik bezeichnen sie die Vergleiche von Zahlen, darüber hinaus werden sie als Symbole für allgemeine Ordnungsrelationen benutzt.

Das Kleiner-als-Zeichen (<) kennzeichnet eine zweistellige Relation, deren semantische Belegung von der verwendeten Algebra abhängt. Implizit wird angenommen, dass die Relation zu „wahr“ ausgewertet wird.

Im täglichen Sprachgebrauch der natürlichen Zahlen bezeichnet man damit die Relation eines echt kleineren (nicht gleich großen!) Wertes gegenüber einem echt größeren Wert. In Präfixnotation bedeutet das: < (a, b) wird zu „wahr“ ausgewertet, also a ist echt kleiner als b.

Die gebräuchlichere Form ist die Infixnotation a < b, wenn a echt kleiner ist als b.

Beispiel

Die natürliche Zahl 3 ist echt kleiner als die natürliche Zahl 4. Man schreibt: $3<4.$ Die Ordnung gibt der Zahlenstrahl der natürlichen Zahlen vor.

Auch die reellen Zahlen sind geordnet: $\pi <{\sqrt {10}}.$

Merksätze und Eselsbrücken

Zur Vermeidung von Verwechslungen zwischen den Größer-als-Zeichen und dem Kleiner-als-Zeichen wird teils – gerade für Schulkinder – der Vergleich mit einem Krokodil als hilfreich angesehen, das stets nach dem größeren „Bissen“ schnappe: „Das Krokodil, das stets das Meiste fressen will“. In der Zeitschrift Kopf und Zahl (Zeitschrift der ZTR zur Behandlung von Rechenschwäche) wird dieser Merksatz kritisiert:

„Einer solchen ‚Erklärung‘ stehe ich skeptisch gegenüber, da sich diese Eselsbrücke nicht aus der mathematischen Logik speist, sondern sich ausschließlich dem Wunsch nach einem kindgemäßen Bild verdankt. Was ist eigentlich, wenn das Reptil nur einen kleinen Hunger hat? (…) Ich bevorzuge stattdessen eine Erklärung, die auf die Entstehung des Symbols Bezug nimmt: ‚Auf derjenigen Seite, auf der das Zeichen größer ist, steht auch die größere Zahl.‘ Auf diese Weise bekommt man auch einen eleganten Übergang zum ‚ist gleich‘ hin: dieses Zeichen ist auf beiden Seiten gleich weit geöffnet.“

– Zeitschrift Kopf und Zahl, 8. Ausgabe, 2007[4]

Auszeichnungssprachen

In manchen Auszeichnungssprachen wie HTML oder XML werden Kleiner-als- und Größer-als-Zeichen zur spracheigenen Kennzeichnung des Beginns und Endes aller (Haupt-)Elemente (Tags) verwendet. Um derartige Auszeichnungen in HTML dennoch darstellen zu können, können ersatzweise die (auch englisch abgekürzt) benannten Elemente < und > verwendet werden – so beispielsweise für das Absatz-Anfangs- und -Endezeichen <p> und </p> (vergleiche auch Absatzzeichen und siehe allgemein unter Maskierungszeichen).

Linguistik

In der Linguistik werden Größer-als- und Kleiner-als-Zeichen als Pfeile verwendet, die von einer grammatisch oder phonetisch ursprünglichen auf eine abgeleitete Form weisen, z. B. altgriechisch ἑλληνικός ἀλφάβητος > neugriechisch ελληνικό αλφάβητο.

Musik

Das gebräuchlichste Zeichen für einen Akzent in der Notation von Musik ist das keilförmige Zeichen $>$ über oder unter der Note. Das Zeichen symbolisiert das rasche Verklingen eines Tones vom lauten in den leisen dynamischen Bereich. Eine noch etwas schärfere Betonung (Akzentuierung) bezeichnet der „Dachakzent“: $\wedge$ .

Darstellung in Computersystemen

Tastatureingabe

Auf deutschen Standard-Tastaturen werden das Kleiner-als-Zeichen und das Größer-als-Zeichen mit der Taste rechts neben der linken Umschalttaste eingegeben.

Auf deutschen Standard-Tastaturen mit der Belegung T2 gemäß DIN 2137:2012-06 wird das Kleiner-Gleich-Zeichen mit der Tastenkombination AltGr+a eingegeben, das Größer-Gleich-Zeichen mit der Tastenkombination AltGr+s.

In macOS wird das Kleiner-Gleich-Zeichen mit der Tastenkombination Alt+< eingegeben, das Größer-Gleich-Zeichen mit der Tastenkombination Alt+⇧+>.

Liste der Vergleichszeichen

Mathematische Vergleichszeichen
Zeichen		Unicode		Bedeutung	Zeichen		Unicode		Bedeutung
=	≠	`U+003D`	`U+2260`	gleich/ungleich	≈	≉	`U+2248`	`U+2249`	fast gleich/nicht fast gleich
<	>	`U+003C`	`U+003E`	kleiner/größer als	≺	≻	`U+227A`	`U+227B`	vorangehend/nachfolgend
≤	≥	`U+2264`	`U+2265`	kleiner/größer als oder gleich	≼	≽	`U+227C`	`U+227D`	vorangehend/nachfolgend oder gleich
≮	≯	`U+226E`	`U+226F`	nicht kleiner/größer als	⊀	⊁	`U+2280`	`U+2281`	nicht vorangehend/nachfolgend
≰	≱	`U+2270`	`U+2271`	weder kleiner/größer als noch gleich	⋠	⋡	`U+22E0`	`U+22E1`	weder vorangehend/nachfolgend noch gleich
≲	≳	`U+2272`	`U+2273`	kleiner/größer als oder äquivalent	≾	≿	`U+227E`	`U+227F`	vorangehend/nachfolgend oder äquivalent
⋜	⋝	`U+22DC`	`U+22DD`	gleich oder kleiner/größer als	⋞	⋟	`U+22DE`	`U+22DF`	gleich oder vorangehend/nachfolgend
⋦	⋧	`U+22E6`	`U+22E7`	kleiner/größer als, aber nicht äquivalent	⋨	⋩	`U+22E8`	`U+22E9`	vorangehend/nachfolgend, aber nicht äquivalent
≴	≵	`U+2274`	`U+2275`	weder kleiner/größer als noch äquivalent	⊰	⊱	`U+22B0`	`U+22B1`	vorangehend/nachfolgend in Relation
≦	≧	`U+2266`	`U+2267`	kleiner/größer als über gleich zu	≨	≩	`U+2268`	`U+2269`	kleiner/größer als, aber nicht gleich
≪	≫	`U+226A`	`U+226B`	viel kleiner/größer als	⋘	⋙	`U+22D8`	`U+22D9`	sehr viel kleiner/größer als
≶	≷	`U+2276`	`U+2277`	kleiner/größer oder größer/kleiner als	≸	≹	`U+2278`	`U+2279`	weder kleiner noch größer als/ weder größer noch kleiner als
⋚	⋛	`U+22DA`	`U+22DB`	kleiner/größer als, gleich oder größer/kleiner als	⋖	⋗	`U+22D6`	`U+22D7`	kleiner/größer als mit Punkt

Zum ASCII-Satz gehören das Kleiner-als-Zeichen (Code 0x3C), das Gleichheitszeichen (Code 0x3D), und das Größer-als-Zeichen (Code 0x3E).

Typografische Varianten

Je nach Tradition des Formelsatzes werden für das Kleiner-gleich-Zeichen und das Größer-gleich-Zeichen geringfügig abweichende Varianten verwendet:

Zeichen		Unicode		LaTeX[5]		HTML
≤	≥	`U+2264`	`U+2265`	`\leq`	`\geq`	`≤`	`≥`
≦	≧	`U+2266`	`U+2267`	`\leqq`	`\geqq`	`≦`	`≧`
⩽	⩾	`U+2A7D`	`U+2A7E`	`\leqslant`	`\geqslant`	`⩽`	`⩾`

In DIN 1302 „Allgemeine mathematische Zeichen und Begriffe“ werden für das Kleiner-gleich- und Größer-gleich-Zeichen die Varianten der ersten Zeile festgelegt. Auch sind es diese Zeichen, die mit der deutschen Standardtastatur (Belegung E1) gemäß DIN 2137-01:2018-12 und der Belegung T2 gemäß der Vorgängernorm DIN 2137-01:2012-06 eingegeben werden können.

Siehe auch

Vergleichsoperator

Einzelnachweise

Thomas Harriot: Artis analyticae praxis, London 1631, Seite 10 (Detail)
Johann Friedrich Ludwig Häseler: Anfangsgründe der Arithmetik. Meyersche Buchhandlung, Lemgo 1802, Teil 1, S. 89.
Clifford A. Pickover: A Passion for Mathematics: Numbers, Puzzles, Madness, Religion, and the Quest for Reality. John Wiley & Sons, 2005, ISBN 978-0-471-69098-6, S. 22. (wordpress.com (Memento des Originals vom 4. März 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 (PDF); abgerufen am 9. Oktober 2015)
Kopf und Zahl. (PDF; 621 KB) In: JOURNAL des Vereins für Lerntherapie und Dyskalkulie e. V. in Zusammenarbeit mit den Mathematischen Instituten zur Behandlung der Rechenschwäche (ZTR), 8. Ausgabe, 2007. Verein für Lern- und Dyskalkulietherapie, 6. November 2007, S. 8, abgerufen am 1. September 2018.
Scott Pakin: The Comprehensive LaTeX Symbol List. (PDF, 21,2 MB) 5. Mai 2021, archiviert vom Original am 18. Juli 2021; abgerufen am 19. Juli 2021 (englisch, siehe Tabellen „Inequalities“ und „𝒜ℳ𝒮 Inequalities“; der Originallink führt zu einem Spiegelserver des CTAN; zum Archivlink vergleiche Datei:Comprehensive LaTeX Symbol List.pdf).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Thomas Harriot: Artis analyticae praxis, London 1631, Seite 10 (Detail)

[2] Johann Friedrich Ludwig Häseler: Anfangsgründe der Arithmetik. Meyersche Buchhandlung, Lemgo 1802, Teil 1, S. 89.

[3] Clifford A. Pickover: A Passion for Mathematics: Numbers, Puzzles, Madness, Religion, and the Quest for Reality. John Wiley & Sons, 2005, ISBN 978-0-471-69098-6, S. 22. (wordpress.com (Memento des Originals vom 4. März 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 (PDF); abgerufen am 9. Oktober 2015)

[4] Kopf und Zahl. (PDF; 621 KB) In: JOURNAL des Vereins für Lerntherapie und Dyskalkulie e. V. in Zusammenarbeit mit den Mathematischen Instituten zur Behandlung der Rechenschwäche (ZTR), 8. Ausgabe, 2007. Verein für Lern- und Dyskalkulietherapie, 6. November 2007, S. 8, abgerufen am 1. September 2018.

[5] Scott Pakin: The Comprehensive LaTeX Symbol List. (PDF, 21,2 MB) 5. Mai 2021, archiviert vom Original am 18. Juli 2021; abgerufen am 19. Juli 2021 (englisch, siehe Tabellen „Inequalities“ und „𝒜ℳ𝒮 Inequalities“; der Originallink führt zu einem Spiegelserver des CTAN; zum Archivlink vergleiche Datei:Comprehensive LaTeX Symbol List.pdf).