Suchverfahren
Die Informatik bezeichnet mit Suchverfahren oder Suchalgorithmus einen Algorithmus, der in einem Suchraum nach Mustern oder Objekten mit bestimmten Eigenschaften sucht. Man unterscheidet einfache und heuristische Suchalgorithmen. Einfache Suchalgorithmen benutzen intuitive Methoden für das Durchsuchen des Suchraumes, während heuristische Suchalgorithmen Wissen über den Suchraum (beispielsweise die Datenverteilung) miteinbeziehen, um die benötigte Suchzeit zu reduzieren.
Die Lösung eines algorithmischen Problems kann allgemein als Suche nach der Lösung in einer Menge von möglichen Lösungen (dem Lösungsraum) verstanden werden. Als Lösung kann der Zielzustand gelten, aber auch der Pfad zum Ziel oder die Reihenfolge von entsprechenden Aktionen. Ist der Suchraum endlich, kann die Suche mit einer geeigneten Suchstrategie immer zu einem Ergebnis führen. Bei unendlichen (Lösungs-)Mengen muss die Suche nach gewissen Kriterien (z. B. nach einer bestimmten Zeit) abgebrochen werden.
Wiederholte Suche in einer endlichen Menge kann dadurch effizient gestaltet werden, dass über den Daten eine Indexstruktur (z. B. in Form eines Suchbaums) erstellt wird, die nach einem bestimmten Kriterium sortiert ist. Dann müssen bei einer Suche nicht mehr alle Einträge betrachtet werden (z. B. beginnt man die Suche in einem Telefonbuch bei dem Buchstaben, mit dem der Name anfängt).
Einfache Suchalgorithmen
Einfache Suchalgorithmen vernachlässigen die spezielle Natur des jeweiligen Problems. Deshalb können sie allgemeiner und abstrakter implementiert werden, wodurch dieselbe Implementierung für eine große Auswahl von Problemen verwendet werden kann. Der Nachteil einfacher Suchalgorithmen sind die entstehenden Kosten: Der Suchraum von Suchproblemen ist im Allgemeinen sehr groß, einfaches Suchen läuft jedoch nur in kleinen Suchräumen in annehmbarer Zeit ab.
Suche in Listen
Algorithmen zur Suche in Listen sind die einfachsten Suchalgorithmen überhaupt. Das Ziel der Suche in Listen ist es, ein bestimmtes Element einer Liste zu finden, von dem der zugehörige Suchschlüssel bekannt ist. Da dieses Problem in der Informatik oft anzutreffen ist, sind die verwendeten Algorithmen – sowie deren Komplexität – sehr gut untersucht.

Der einfachste Suchalgorithmus für Listen ist die lineare Suche. Bei ihr wird solange ein Element nach dem anderen durchlaufen, bis ein Element mit dem gesuchten Schlüssel angetroffen wird. Die lineare Suche hat eine Laufzeit von (n ist die Anzahl der Elemente der Liste) und kann sowohl auf sortierte als auch unsortierte Listen angewendet werden. Ein fortgeschrittenes Verfahren ist die binäre Suche mit einer Laufzeit von . Für große Listen ist sie viel effizienter als die lineare Suche, setzt jedoch voraus, dass die Liste vorher sortiert wurde und ein wahlfreier Zugriff auf die Elemente möglich ist. Die Interpolationssuche, auch Intervallsuche genannt, ist eine Verbesserung der binären Suche, die eine Gleichverteilung der Daten voraussetzt. Die Laufzeit ist nur für sehr große Datenmengen besser als die der binären Suche. Ein weiterer Suchalgorithmus für Listen ist der Grover-Algorithmus, der auf Quantencomputern zum Einsatz kommt und quadratisch schneller als die klassische lineare Suche für unsortierte Listen abläuft. Für die Suche in Listen kann auch Hashing verwendet werden, das im Durchschnitt eine konstante Zeit , im schlechtesten Fall jedoch lineare Zeit benötigt.
Suche in Bäumen
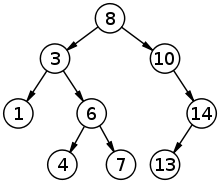
Die Suche in Bäumen ist die Königsdisziplin unter den Suchalgorithmen. Sie durchsucht Knoten von Bäumen, unabhängig davon, ob der Baum explizit oder implizit (während der Suche generiert) ist. Dabei wird folgendes Prinzip angewendet: Ein Knoten wird aus einer Datenstruktur entnommen. Seine Kindknoten werden untersucht und gegebenenfalls der Datenstruktur hinzugefügt. Je nach Auswahl der Datenstruktur kann der Baum in verschiedenen Reihenfolgen durchsucht werden. Die Verwendung einer Warteschlange führt so zu einer Breitensuche, bei der der Baum Ebene für Ebene durchlaufen wird. Bei Verwendung eines Stacks hingegen wird jeweils bis zu einem Blatt gesucht und erst anschließend mit dem nächsten Kindknoten fortgefahren. Dies wird als Tiefensuche bezeichnet.
Suche in Graphen
Viele Probleme der Graphentheorie können mit Hilfe von Suchalgorithmen gelöst werden. Beispiele für diese Probleme sind das Problem des Handlungsreisenden, die Berechnung kürzester Pfade und die Konstruktion eines minimalen Spannbaums. Die entsprechenden Algorithmen sind zum Beispiel Kruskals Algorithmus, Dijkstras Algorithmus oder Prims Algorithmus, die als Erweiterungen der Algorithmen für die Suche in Bäumen gesehen werden können.
Heuristische (Informierte) Suchalgorithmen
Strategien, die das Auffinden von Lösungen beschleunigen können, bezeichnet man als Heuristiken. Typische Heuristiken sind Faustregeln, die Orientierung an Beispielen und die Nachbildung des menschlichen Problemlöseprozesses. Demnach können die Verfahren in uninformierte (auch blinde Suche genannt) und informierte (Nutzung von Heuristiken) unterschieden werden. Das Studium verschiedener Verfahren zur heuristischen Suche, die Entwicklung und Implementation neuer Verfahren und ihre Anwendung auf verschiedene Problembereiche rechnet man üblicherweise zum algorithmischen Kern der Künstlichen Intelligenz. Dazu gehören z. B. das automatische Beweisen, die Steuerung von Robotern und, als typische Vertreter, insbesondere Spiele. Gemeint sind sowohl Zwei-Personen-Spiele (Nullsummenspiele mit vollständiger Information) wie z. B. Schach, Dame, Mühle als auch Ein-Personen-Spiele wie Schiebepuzzles oder Solitaire. Die klassischen Verfahren zur heuristischen Suche sind A*, IDA*, bidirektionale Suchschemata, das Minimax-Verfahren, Alpha-Beta-Suche.
Heuristische Suchalgorithmen kommen auch dann zum Einsatz, wenn ein Algorithmus zur Problemlösung zu rechenintensiv ist. In diesem Fall wird ein gewisser Fehler in Kauf genommen – also auch eine nicht optimale Lösung akzeptiert – wenn dafür die eingesetzte Rechenzeit deutlich reduziert werden kann.
Optimierende Suche
Diese Art der Suche löst Optimierungsaufgaben, bei der eine Reihe von Variablen mit Werten belegt werden muss. Da es sich dabei um sehr viele Variablen mit sehr großem Wertebereich handeln kann, ist der Suchbereich sehr groß und herkömmliche Suchverfahren versagen.
Kombinatorische Suche und Backtracking sind Verfahren, die bei der optimierenden Suche zum Einsatz kommen, vor allem bei diskreten Variablen.
Zur analogen Suche nach Minima oder Maxima von mehrdimensionalen Funktionen gibt es eine ganze Anzahl an numerischen Optimierungsverfahren, die je nach den jeweiligen Ausgangsbedingungen eingesetzt werden.
Ein anderes Vorgehen beruht auf dem Feedback durch den Nutzer, der die Relevanz der Ergebnisse zu bewerten hat, siehe Relevanz-Feedback.
Andere Suchverfahren
Suchverfahren für Zeichenketten suchen in Zeichenketten nach dem Auftreten eines Schlüssels. Bekannte Vertreter sind der Algorithmus von Knuth-Morris-Pratt, der Algorithmus von Boyer-Moore sowie der Karp-Rabin-Algorithmus. Siehe dazu: String-Matching-Algorithmus.
Evolutionäre Algorithmen benutzen Ideen aus der Evolutionstheorie als Heuristiken, um schneller gute Ergebnisse zu bekommen.
Simulierte Abkühlung (simulated annealing) ist ein auf Wahrscheinlichkeit beruhender Suchalgorithmus.
Adversarial Search wird im Bereich der künstlichen Intelligenz eingesetzt.
Leistungsunterschiede der Suchverfahren
In den No-Free-Lunch-Theoremen wurde gezeigt, dass – gemittelt über alle mathematisch formulierbaren Probleme – alle Suchverfahren gleich gut sind. Einen Leistungsvorsprung zeigt ein Suchverfahren jeweils nur auf einer speziellen Klasse von Problemen.
Siehe auch
Weblinks
- R. Poli, W. B. Langdon, N. F. McPhee: A Field Guide to Genetic Programming. Lulu.com, 2008, ISBN 978-1-4092-0073-4. (researchgate.net)