Alpha-Beta-Suche
Die Alpha-Beta-Suche (auch Alpha-Beta-Cut oder Alpha-Beta-Pruning genannt) ist eine optimierte Variante des Minimax-Suchverfahrens, also eines Algorithmus zur Bestimmung eines optimalen Zuges bei Spielen mit zwei gegnerischen Parteien. Während der Suche werden zwei Werte – Alpha und Beta – aktualisiert, die angeben, welches Ergebnis die Spieler bei optimaler Spielweise erzielen können. Mit Hilfe dieser Werte kann entschieden werden, welche Teile des Suchbaumes nicht untersucht werden müssen, weil sie das Ergebnis der Problemlösung nicht beeinflussen können.
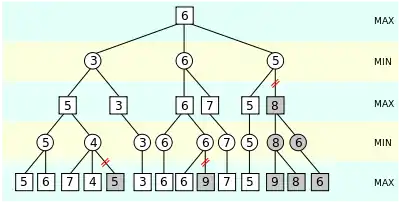
Die einfache (nicht optimierte) Alpha-Beta-Suche liefert exakt dasselbe Ergebnis wie die Minimax-Suche.
Informelle Beschreibung
Der Minimax-Algorithmus analysiert den vollständigen Suchbaum. Dabei werden aber auch Knoten betrachtet, die in das Ergebnis (die Wahl des Zweiges an der Wurzel) nicht einfließen. Die Alpha-Beta-Suche ignoriert alle Knoten, von denen im Moment, da sie von der Suche erreicht werden, bereits feststeht, dass sie das Ergebnis nicht beeinflussen können.
Ein anschauliches Beispiel für die Funktionsweise ist ein Zweipersonenspiel, bei dem der erste Spieler eine von mehreren Taschen auswählt und von seinem Gegenspieler den Gegenstand mit geringstem Wert aus dieser Tasche erhält.
Der Minimax-Algorithmus durchsucht für die Auswahl alle Taschen vollständig und benötigt somit viel Zeit. Die Alpha-Beta-Suche hingegen durchsucht zunächst nur die erste Tasche vollständig nach dem Gegenstand mit minimalem Wert. In allen weiteren Taschen wird nur solange gesucht, bis der Wert eines Gegenstands dieses Minimum erreicht oder unterschreitet. Dann steht fest, dass diese Tasche für den ersten Spieler nicht besser als die erste ist, und die Suche darin kann abgebrochen werden. Andernfalls ist diese Tasche eine bessere Wahl, und ihr minimaler Wert dient für die weitere Suche als neue Grenze.
Ähnliche Situationen sind jedem Schachspieler vertraut, der gerade einen konkreten Zug darauf prüft, ob er ihm vorteilhaft erscheint. Findet er bei seiner Analyse des Zuges eine für sich selbst ungünstige Erwiderung des Gegners, dann wird er diesen Zug als „widerlegt“ ansehen und verwerfen. Es wäre sinnlos, noch weitere Erwiderungen des Gegners zu untersuchen, um festzustellen, ob der Gegner noch effektivere Widerlegungen besitzt und wie schlecht der betrachtete Zug tatsächlich ist.[1]
Der Algorithmus
Die Alpha-Beta-Suche arbeitet prinzipiell genauso wie obige informelle Beschreibung. Die Idee ist, dass zwei Werte (Alpha und Beta) weitergereicht werden, die das Worst-Case-Szenario der Spieler beschreiben. Der Alpha-Wert ist das Ergebnis, das Spieler A mindestens erreichen wird, der Beta-Wert ist das Ergebnis, das Spieler B höchstens erreichen wird. (Hier ist zu beachten, dass es für Spieler B darum geht, ein möglichst niedriges Ergebnis zu erhalten, da er ja „minimierend“ spielt!)
Besitzt ein maximierender Knoten (von Spieler A) einen Zug, dessen Rückgabe den Beta-Wert überschreitet, wird die Suche in diesem Knoten abgebrochen (Beta-Cutoff, denn Spieler B würde A diese Variante erst gar nicht anbieten, weil sie sein bisheriges Höchst-Zugeständnis überschreiten würde). Liefert der Zug stattdessen ein Ergebnis, das den momentanen Alpha-Wert übersteigt, wird dieser entsprechend nach oben angehoben.
Analoges gilt für die minimierenden Knoten, wobei bei Werten kleiner als Alpha abgebrochen wird (Alpha-Cutoff) und der Beta-Wert nach unten angepasst wird.
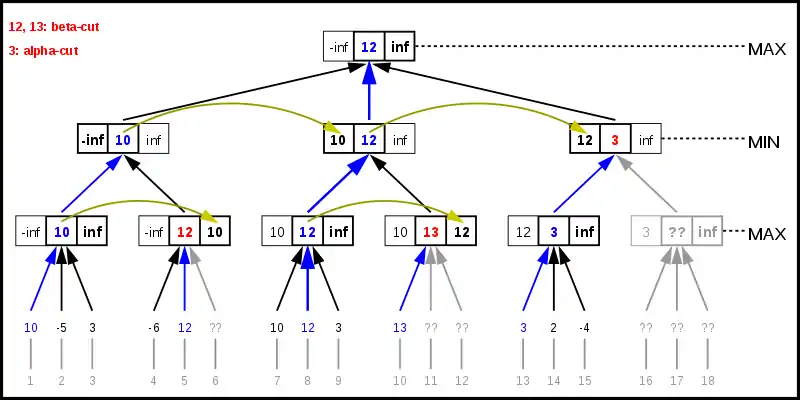
Obige Abbildung zeigt einen Beispielbaum mit 18 Blättern, von denen nur 12 ausgewertet werden. Die drei umrandeten Werte eines inneren Knotens beschreiben den Alpha-Wert, den Rückgabewert und den Beta-Wert.
Der Suchalgorithmus verwendet ein sogenanntes Alpha-Beta-Fenster, dessen untere Grenze der Alpha-Wert und dessen obere Grenze der Beta-Wert darstellt. Dieses Fenster wird zu den Kindknoten weitergegeben, wobei in der Wurzel mit dem maximalen Fenster [-inf, inf] begonnen wird. Die Blätter 1, 2 und 3 werden von einem maximierenden Knoten ausgewertet und der beste Wert 10 wird dem minimierenden Vaterknoten übergeben. Dieser passt den Beta-Wert an und übergibt das neue Fenster [-inf, 10] dem nächsten maximierenden Kindknoten, der die Blätter 4, 5 und 6 besitzt. Der Rückgabewert 12 von Blatt 5 ist aber so gut, dass er den Beta-Wert 10 überschreitet. Somit muss Blatt 6 nicht mehr betrachtet werden, weil das Ergebnis 12 dieses Teilbaumes besser ist als das des linken Teilbaumes und deshalb vom minimierenden Spieler nie gewählt werden würde.
Ähnlich verhält es sich beim minimierenden Knoten mit dem 3-Alpha-Cutoff. Obwohl dieser Teilbaum erst teilweise ausgewertet wurde, ist klar, dass der maximierende Wurzelknoten diese Variante niemals wählen würde, weil der minimierende Knoten ein Ergebnis von höchstens 3 erzwingen könnte, während aus dem mittleren Teilbaum das Ergebnis 12 sichergestellt ist.
Implementierung
Anmerkung: Unterschiede zum einfachen Minimax-Algorithmus sind gelb hinterlegt.
Hauptprogramm (Auszug):
gespeicherterZug = NULL;
int gewuenschteTiefe = 4;
int bewertung = max(gewuenschteTiefe,
-unendlich, +unendlich);
if (gespeicherterZug == NULL)
es gab keine weiteren Zuege mehr (Matt oder Patt);
else
gespeicherterZug ausführen;
Die normale Variante lautet:
int max(int tiefe,
int alpha, int beta) {
if (tiefe == 0 or keineZuegeMehr(spieler_max))
return bewerten();
int maxWert = alpha;
Zugliste = generiereMoeglicheZuege(spieler_max);
for each (Zug in Zugliste) {
fuehreZugAus(Zug);
int wert = min(tiefe-1,
maxWert, beta);
macheZugRueckgaengig(Zug);
if (wert > maxWert) {
maxWert = wert;
if (tiefe == gewuenschteTiefe)
gespeicherterZug = Zug;
if (maxWert >= beta)
break;
}
}
return maxWert;
}
int min(int tiefe,
int alpha, int beta) {
if (tiefe == 0 or keineZuegeMehr(spieler_min))
return bewerten();
int minWert = beta;
Zugliste = generiereMoeglicheZuege(spieler_min);
for each (Zug in Zugliste) {
fuehreZugAus(Zug);
int wert = max(tiefe-1,
alpha, minWert);
macheZugRueckgaengig(Zug);
if (wert < minWert) {
minWert = wert;
if (minWert <= alpha)
break;
}
}
return minWert;
}
Die NegaMax-Variante lautet:
int miniMax(int spieler, int tiefe,
int alpha, int beta) {
if (tiefe == 0 or keineZuegeMehr(spieler))
return bewerten(spieler);
int maxWert = alpha;
Zugliste = generiereMoeglicheZuege(spieler);
for each (Zug in Zugliste) {
fuehreZugAus(Zug);
int wert = -miniMax(-spieler, tiefe-1,
-beta, -maxWert);
macheZugRueckgaengig(Zug);
if (wert > maxWert) {
maxWert = wert;
if (tiefe == gewuenschteTiefe)
gespeicherterZug = Zug;
if (maxWert >= beta)
break;
}
}
return maxWert;
}
Anmerkung: Während die Standard-Implementierung für einen Spieler maximiert und für den anderen Spieler minimiert, maximiert die Negamax-Variante für beide Spieler und vertauscht und negiert Alpha und Beta bei der Rekursion. Daraus folgt, dass sich die Bewertungsfunktion in beiden Implementierungen unterschiedlich verhalten muss.
- Standard-Implementierung: Je besser die Brettstellung für den maximierenden Spieler ist, desto größer ist der Rückgabewert der Bewertungsfunktion (Funktion bewerten()). Je besser sie für den minimierenden Spieler ist, desto kleiner ist der Rückgabewert.
- Negamax-Implementierung: Da beide Spieler maximieren, muss die Bewertungsfunktion umso größere Werte liefern, je besser die Brettposition des gerade Ziehenden ist (Funktion bewerten(spieler)). Der Wert wird immer aus dessen Sicht angegeben.
Optimierungen
Kann man auf Grund der Komplexität des betrachteten Spiels den Spielbaum nur bis zu einer gewissen Tiefe berechnen, sind grundsätzlich zwei Optimierungsansätze möglich. Zum einen kann die Bewertungsfunktion verbessert werden, zum anderen bietet der Alpha-Beta-Algorithmus selbst Optimierungspotential. Je besser die Bewertungsfunktion ist, desto weniger tief muss der Spielbaum betrachtet werden, um eine gewisse Spielstärke zu erlangen.
Im Folgenden wird nur auf Optimierungen der Alpha-Beta-Suche eingegangen.
Vorsortierung der Züge
Anders als beim Minimax-Algorithmus spielt bei der Alpha-Beta-Suche die Reihenfolge, in der Kindknoten (Züge) bearbeitet werden, eine wesentliche Rolle. Je schneller das Alpha-Beta-Fenster verkleinert wird, desto mehr Cutoffs werden erreicht. Deshalb ist es wichtig, zuerst die Züge zu betrachten, die das beste Ergebnis versprechen. In der Praxis werden verschiedene Heuristiken verwendet. Bei Schach z. B. kann man die Züge danach sortieren, ob bzw. welche Figur geschlagen wird, oder auch welche Figur schlägt. „Turm schlägt Dame“ wird demnach vor „Turm schlägt Turm“ einsortiert und „Bauer schlägt Turm“ wird zwischen beiden einsortiert.
Principal-Variation-Suche
Ein Knoten bei der Alpha-Beta-Suche gehört einer von drei Kategorien an (bezogen auf die NegaMax-Variante):
- Alpha-Knoten: Jeder Folgezug liefert einen Wert kleiner oder gleich Alpha, was bedeutet, dass hier kein guter Zug möglich ist.
- Beta-Knoten: Mindestens ein Folgezug liefert einen Wert größer oder gleich Beta, was einen Cutoff bedeutet.
- Principal-Variation-Knoten: Mindestens ein Folgezug liefert einen Wert größer als Alpha, aber alle liefern einen Wert kleiner Beta.
Manchmal kann man frühzeitig erkennen, um welchen Knoten es sich handelt. Liefert der erste getestete Folgezug einen Wert größer gleich Beta, dann ist es ein Beta-Knoten. Liefert er einen Wert kleiner gleich Alpha, dann ist es möglicherweise ein Alpha-Knoten (vorausgesetzt, die Züge sind gut vorsortiert). Liefert er aber einen Wert zwischen Alpha und Beta, so handelt sich möglicherweise um einen Principal-Variation-Knoten.
Die Principal-Variation-Suche nimmt nun an, dass ein Folgezug, der einen Wert zwischen Alpha und Beta liefert, sich als bester möglicher Zug herausstellen wird. Deshalb wird das Alpha-Beta-Fenster im Folgenden auf das Minimum (alpha, alpha+1) verkleinert (Nullfenster), um eine maximale Anzahl an Cutoffs zu erreichen, aber dennoch die verbleibenden Züge als schlechter zu beweisen.
Stellt sich bei Suche mit diesem Nullfenster heraus, dass der Zug einen Wert größer alpha hat (aber das Ergebnis noch kleiner als beta ist, denn sonst kann man gleich einen beta-Schnitt machen), muss die Suche mit einem größeren Fenster wiederholt werden: Da man aus der Nullfenstersuche schon eine untere Schranke für den Zugwert kennt, sollte das Fenster bei der Wiederholungssuche von diesem Wert bis beta reichen. Wegen der zuweilen nötigen Wiederholungssuche erreicht man durch dieses Verfahren nur dann Erfolge, wenn die Züge gut vorsortiert wurden, weil dadurch Fehleinordnungen in eine der drei genannten Kategorien minimiert werden, d. h., es wird unwahrscheinlich, dass ein Folgezug einen besseren Wert als alpha hat und die Suche wiederholt werden muss. Andererseits können Principal-Variation-Knoten in Verbindung mit dem Iterative Deepening auch für die Vorsortierung der Züge verwendet werden.
int AlphaBeta(int tiefe, int alpha, int beta)
{
if (tiefe == 0)
return Bewerten();
BOOL PVgefunden = FALSE;
best = -unendlich;
Zugliste = GeneriereMoeglicheZuege();
for each (Zug in Zugliste)
{
FuehreZugAus(Zug);
if (PVgefunden)
{
wert = -AlphaBeta(tiefe-1, -alpha-1, -alpha);
if (wert > alpha && wert < beta)
wert = -AlphaBeta(tiefe-1, -beta, -wert);
} else
wert = -AlphaBeta(tiefe-1, -beta, -alpha);
MacheZugRueckgaengig(Zug);
if (wert > best)
{
if (wert >= beta)
return wert;
best = wert;
if (wert > alpha)
{
alpha = wert;
PVgefunden = TRUE;
}
}
}
return best;
}
Iterative Tiefensuche (Iterative Deepening)
Die iterative Tiefensuche ist die schrittweise Erhöhung der Tiefe des Suchbaumes. Da die Alpha-Beta-Suche eine Tiefensuche ist, kann man meist vorher nicht bestimmen, wie lange die Berechnung dauern wird. Deshalb beginnt man mit einer geringen Suchtiefe und erhöht diese schrittweise. Das Ergebnis einer Berechnung kann benutzt werden, um bei erhöhter Suchtiefe die Züge besser vorzusortieren.
Aspiration windows
Aspiration windows werden zusammen mit der iterativen Tiefensuche verwendet. Grundsätzlich beginnt die Alpha-Beta-Suche an der Wurzel mit einem maximalen Fenster. Bei der iterativen Tiefensuche kann aber angenommen werden, dass eine neue Berechnung mit höherer Tiefe einen ähnlichen Ergebniswert liefern wird. Deshalb kann das Suchfenster initial auf einen (relativ) kleinen Bereich um den Ergebniswert der vorherigen Berechnung gesetzt werden. Stellt sich heraus, dass dieses Fenster zu klein war, muss (ähnlich wie bei der Principal-Variation-Suche) die Suche mit größerem oder maximalem Fenster wiederholt werden.
Killer-Heuristik
Die Killer-Heuristik ist eine spezielle Art der Zugvorsortierung. Man nimmt hierbei an, dass Züge, die einen Cutoff verursacht haben, auch in anderen Teilen des Suchbaumes (bei gleicher Tiefe) einen Cutoff verursachen werden. Deshalb werden sie künftig immer zuerst betrachtet, sofern sie in der gerade betrachteten Spielposition gültige Züge darstellen. Diese Heuristik kann nicht bei allen Spielen sinnvoll angewendet werden, da die Aussicht darauf, dass diese so genannten Killerzüge auch in anderen Teilen des Suchbaumes noch gültige Züge sind, von der Art des Spiels abhängt.
Ruhesuche
Bei der Alpha-Beta-Suche bzw. dem Minimax-Algorithmus ist es wenig günstig, wenn die Suche beim Erreichen einer festen Suchtiefe abgebrochen wird. Auf diese Weise könnte zum Beispiel beim Schach das Schlagen eines gedeckten Bauern durch die Dame als vorteilhaft erscheinen, wenn das Zurückschlagen unterhalb des Suchhorizonts liegen und daher vom Algorithmus „übersehen“ würde. Aus diesem Grund erfolgt der Übergang von der Alpha-Beta-Suche zur Bewertungsfunktion dynamisch, und zwar derart, dass unterhalb der Mindestsuchtiefe in Bezug auf die Bewertungsfunktion eine annähernde Konstanz abgewartet wird. Diese „Ruhe“ in Bezug auf die Werte der Bewertungsfunktion ist namensgebend für die Verfahrensweise, man spricht von einer Ruhesuche (englisch Quiescence search). Beim Schach führt die Ruhesuche insbesondere dazu, dass ein Schlagabtausch bis zum Ende analysiert wird.
Null-Zug-Suche
Die Null-Zug-Suche ist eine Optimierung, die sich die Tatsache zu Nutze macht, dass bei manchen Spielen (z. B. Schach) das Zugrecht von Vorteil ist.
Vergleich von Minimax und AlphaBeta
Nachfolgende Tabelle zeigt eine Beispielberechnung einer Schachstellung bei konstanter Suchtiefe von vier Halbzügen (jeder Spieler zieht zweimal). Es wurde der normale Minimax-Algorithmus angewendet und Alpha-Beta ohne Zugsortierung und mit (einfacher) Zugsortierung. Die Prozentangabe bei den Cutoffs beziehen sich auf den gesamten Suchbaum und beschreibt, wie viel des gesamten Suchbaumes nicht ausgewertet wurde. Es handelt sich dabei um Schätzungen, denen zugrunde liegt, dass die Teilbäume in etwa gleich groß sind (bei Cutoffs ist nicht bekannt, wie groß der weggeschnittene Teilbaum wirklich wäre).
| Algorithmus | Bewertungen | Cutoffs | Anteil der Cutoffs | Rechenzeit in Sekunden |
|---|---|---|---|---|
| Minimax | 28.018.531 | 0 | 0,00 % | 134,87 s |
| AlphaBeta | 2.005.246 | 136.478 | 91,50 % | 9,88 s |
| AlphaBeta + Zugsortierung | 128.307 | 27.025 | 99,28 % | 0,99 s |
Es ist deutlich zu erkennen, dass die Alpha-Beta-Suche eine erhebliche Geschwindigkeitssteigerung gegenüber Minimax bedeutet. Auch die Zugsortierung verbessert die Rechenzeit in diesem Beispiel um den Faktor 10. Die Tatsache, dass mit Zugsortierung die Anzahl der Cutoffs absolut sinkt, lässt sich dadurch erklären, dass diese auf höheren Ebenen im Suchbaum erfolgen und somit größere Teile weggeschnitten werden.
Geschichte
Während die zentrale Bedeutung des Minimax-Algorithmus für die Schachprogrammierung bereits von deren Pionieren Alan Turing und Claude Shannon in den 1940er-Jahren hervorgehoben wurde, liegen die Anfänge der Alpha-Beta-Suche in den späten 1950er-Jahren, wobei zunächst nur Alpha-Cutoffs verwendet wurden.[2] Erst in den 1960er-Jahren wurde der Alpha-Beta-Algorithmus zum festen Bestandteil von Schachprogrammen. Eine erste, allerdings unveröffentlichte Beschreibung stammt aus dem Jahr 1963.[3] Die erste ausführliche Untersuchung erschien 1975.[4]
Literatur
- Jörg Bewersdorff: Glück, Logik und Bluff. Mathematik im Spiel – Methoden, Ergebnisse und Grenzen. 5. Auflage. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-0775-5, doi:10.1007/978-3-8348-9696-4, S. 177–197 (Kapitel 2.10).
- Alexander Reinefeld: Entwicklung der Spielbaum-Suchverfahren: Von Zuses Schachhirn zum modernen Schachcomputer. In: Wolfgang Reisig & Johann-Christoph Freytag (Hrsg.): Informatik. Aktuelle Themen im historischen Kontext. Springer, Berlin/Heidelberg/New York 2006, ISBN 978-3-540-32742-4, doi:10.1007/3-540-32743-6_11, S. 241–276.
- Wolfgang Ertel: Grundkurs Künstliche Intelligenz: Eine praxisorientierte Einführung, Computational Intelligence. 4. Auflage. Springer Vieweg, Wiesbaden 2016, ISBN 978-3658135485, doi:10.1007/978-3-658-13549-2, S. 125–127.
Weblinks
- Burkhard Monien, Ulf Lorenz & Daniel Warner: Der Alphabeta-Algorithmus für Spielbaumsuche. 2006.
- Visualisierung der Alpha-Beta-Suche als Java-Applet für beliebige Spielbäume
Fußnoten
- Jörg Bewersdorff: Glück, Logik und Bluff. Mathematik im Spiel – Methoden, Ergebnisse und Grenzen. 5. Auflage. 2010, S. 184.
- Allen Newell, J. C. Shaw & H. A. Simon: Chess-playing programs and the problem of complexity. In: IBM Journal of Research and Development. Band 2, Heft 4, 1958, doi:10.1147/rd.24.0320, S. 330–335 (PDF; 2,172 MB).
- D. J. Edwards & T. P. Hart: The alpha-beta heuristic (= AI Memos. 030). Massachusetts Institute of Technology, 1963 (PDF; 288 kB).
- Donald E. Knuth & Ronald W. Moore: An analysis of alpha-beta Pruning. In: Artificial Intelligence. Band 6, Heft 4, 1975, doi:10.1016/0004-3702(75)90019-3, S. 293–326