Geostatistik
Die Geostatistik oder räumliche Statistik ist ein Teilgebiet der Statistik, welches unter Einbezug der Wahrscheinlichkeitsrechnung ortsabhängige Daten (Geodaten) auswertet und modelliert.[1] Die Hauptanwendung der Geostatistik liegt somit in der stochastischen Validierung von Messdaten und der Schätzung (Approximation) über diese hinaus.
Die grundlegende Annahme der Geostatistik ist, dass benachbarte Daten sich ähneln und somit Punkte über die Distanz zueinander korrelieren. So können z. B. Relief- oder Temperaturkarten erstellt werden, ohne dass jeder Punkt vermessen werden muss, da in der Regel zwischen Temperaturen oder Höhenlagen ein Mittel auftritt.
Geschichte
Die Ursprünge der Geostatistik gehen auf die Lagerstättenkunde in den 1950er Jahren zurück, als Danie. G. Krige die ersten Konzepte entwickelte, um mit statistischen Verfahren und guten Schätzmethoden teuere Probebohrungen zu minimieren und damit die wirtschaftliche Gewinnspanne im Bergbau zu steigern. Als Begründer der Geostatistik selbst gilt Georges Matheron, der 1971 die als "Theorie der regionalisierten Variablen" bekannten mathematisch-theoretischen Grundlagen für die Disziplin veröffentlichte.[1]
Geostatistische Parameter
Der Schätzwert für eine physikalische Größe (wie die Oberflächentemperatur) an einem Schätzort ist aufgrund der räumlichen Korrelation stärker von den Messwerten benachbarter als von solchen entfernter Messorte abhängig. Für die Abschätzung sind diese benachbarten Messwerte daher stärker zu berücksichtigen. Dabei unterscheidet man zwei Methoden, die nichtstatistischen und die statistischen Interpolationsverfahren, wobei letztere auf einem Geostatistischen Modell (häufig einem speziellen Zufallsfeld) beruhen.
Um herauszufinden, bis zu welcher maximalen Entfernung (Reichweite) und in welchem Maße Messwerte von benachbarten oder weiter entfernten Messwerten abhängen, werden sogenannte experimentelle Semivariogramme modelliert: Für alle Entfernungen (als x-Werte), die jeweils zwei Messorte des Datensatzes zueinander haben, werden die Differenzen der jeweiligen Messwerte (als y-Werte) aufgetragen: Die wachsende Unähnlichkeit mit wachsender Entfernung spiegelt sich in der Zunahme der y-Werte mit steigenden x-Werten bis zu einem bestimmten Grenzwert wider. Diese Abhängigkeit wird mit einer Modellfunktion, zum Beispiel einer quadratischen Funktion, ausgedrückt.
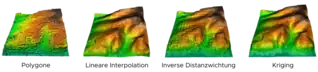
Die Funktion, die aus der Analyse der Messwerte gewonnen wurde, ist die Grundlage für die nachfolgende Interpolation einer Verteilung von Schätzwerten im Raum. Als Interpolationsmethode hat sich das Kriging-Verfahren gegenüber anderen Methoden wie der Linearen Interpolation, Polygonmethode und Inversen Distanzwichtung etabliert. Beim Kriging erhalten die Messwerte je nach Nähe zum gesuchten Schätzwert in Abhängigkeit vom modellierten Semivariogramm unterschiedliche Gewichtungsfaktoren, mit denen sie in die Berechnung des Schätzwerts eingehen (Gegenbeispiel: arithmetischer Mittelwert als Schätzer: alle Messwerte erhalten ohne Unterschied dasselbe Gewicht).
Voraussetzung für die Interpolation ist, dass im Untersuchungsgebiet die Messwertverteilung homogen ist. In der Regel wird dies in der Praxis auf die stochastische Stationarität 2. Ordnung abgeschwächt, also dass der Erwartungswert einer Zufallsfunktion unabhängig von ihrem Ort und nur eine Funktion des Abstandsvektors ist.[2] Beispiel für Inhomogenität: der Aluminium-Gehalt von Gesteinen eines Untersuchungsgebiets, in dem durch Versatz an einer Störung zwei völlig unterschiedliche Gesteinseinheiten nebeneinander vorliegen und ohne Übergangszone aneinandergrenzen.
Für das Beispiel Oberflächentemperatur eines Sees wäre das Ergebnis des Krigings eine Verteilung von Schätzwerten in der Ebene, die zum Beispiel als Isothermen-Karte oder Oberflächenrelief („fliegender Teppich“) mit der Höhen-Achse als Temperatur-Achse visualisiert werden kann.
Anwendungsbereich
Die Geostatistik ist ein elementarer Bestandteil der Lagerstättenkunde und des Bergbaus, da beispielsweise über Volumen-/Blockschätzung die Gesamtvorkommen einer Lagerstätte oder über Kokriging die Abbauwürdigkeit von Erzen (Reinheit) bewertet werden kann. Über Flächenschätzungen können digitale Geländemodelle und Karten erstellt, die Ausbreitung von Stoffkonzentrationen in Böden und im Grundwasser, sowie Nährstoffverhältnisse, Schwermetall- oder Schadstoffkonzentrationen abgeschätzt oder die räumliche Verteilung von Niederschlägen, Lufttemperaturen und Windfeldern modelliert werden. Daher findet die Geostatistik untergeordnet auch in anderen Geowissenschaften wie Klimatologie, Hydrologie, Bodenkunde, Hydrogeologie sowie in der Geographie anwendung.[1]
Standardliteratur
- H. Wackernagel: Multivariate Geostatistics. Springer, Berlin/ Heidelberg/ New York 1995, ISBN 3-540-60127-9.
- J. P. Chiles, P. Delfiner: Geostatistics: Modelling Spatial Uncertainty. Wiley, New York 1999, ISBN 0-471-08315-1.
- N. Cressie: Statistics for Spatial Data. World Scientific, Singapore 2007.
Einzelnachweise
- Geostatistik. In: Lexikon der Kartographie und Geomatik. Spektrum, abgerufen am 12. Oktober 2021.
- Stationarität. In: Lexikon der Kartographie und Geomatik. Spektrum, abgerufen am 30. Januar 2022.