Schere, Stein, Papier
Schere, Stein, Papier (auch Schnick, Schnack, Schnuck; Fli, Fla, Flu; Ching, Chang, Chong; Klick, Klack, Kluck; Stein schleift Schere; Schnibbeln, Knobeln oder Schniekern) ist ein sowohl bei Kindern als auch Erwachsenen beliebtes und weltweit verbreitetes Spiel. Zwei Spieler wählen je eins der drei möglichen Symbole Schere, Stein oder Papier und zeigen dieses dann auf ein Kommando gleichzeitig (schlagartig) mit Hilfe einer ihrer Hände an. Da jedes Symbol gegen ein anderes gewinnen oder verlieren kann, steht immer einer der Spieler als Gewinner fest. Zu Unentschieden kommt es, wenn beide Spieler dasselbe Symbol wählen. Das Spiel wird in diesem Fall wiederholt.
Es wird in Analogie zum Münzwurf auch oft zur Entscheidung zwischen zwei Möglichkeiten benutzt, zum Beispiel dafür, welche Fußball-Mannschaft den ersten Anstoß ausführt.
.png.webp) Die Geste für Schere
Die Geste für Schere.png.webp) Die Geste für Papier
Die Geste für Papier.png.webp) Die Geste für Stein
Die Geste für Stein
Spielprinzip
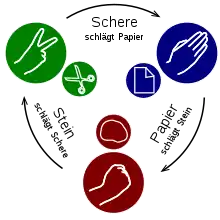
Das Spiel wird ausschließlich mit den Händen gespielt. Den Handhaltungen werden Symbole zugeordnet, die einander „schlagen“ können. Die drei Hauptfiguren sind Schere, Stein und Papier. Das Papier wird durch eine flache Hand mit ungespreizten Fingern dargestellt, das Symbol der Schere ist der gespreizte Zeige- und Mittelfinger, und der Stein wird durch eine Faust symbolisiert. Die Wertigkeit der Symbole gegeneinander ergibt sich aus dem jeweils Dargestellten: Die Schere schneidet das Papier (Schere gewinnt), das Papier wickelt den Stein ein (Papier gewinnt), und der Stein macht die Schere stumpf (Stein gewinnt). Entscheiden sich beide Spieler für dasselbe Symbol, wird das Spiel als unentschieden gewertet und wiederholt.
Schere, Stein, Papier wird oft im Best-of-Three-Modus gespielt.
Ziel des Spiels
Ziel des Spieles ist es, eine höherwertige Handhaltung zu haben als der Gegner. Damit keiner der Spieler einen Nachteil durch verfrühtes Zeigen seiner Handhaltung bekommt, bewegen beide Spieler ihre rechte Hand noch zur Faust geballt vor sich auf und ab und sprechen dabei zusammen den Namen des Spiels, zählen bis drei oder Ähnliches. Diese Bewegung dient der Spannung und ist außerdem eine rhythmische Synchronisierungshilfe. Gleichzeitig mit dem letzten Wort des Spielnamens (Papier, Schnuck, Chong oder Kluck) offenbaren die Spieler sich gegenseitig ihre Handhaltung. In einer abgewandelten Form hakeln die Spieler beim Synchronisieren ihre kleinen Finger ineinander.
Logik und Psychologie des Spiels
Wenn der Mensch rein zufällig eine der drei Spielfiguren auswählen könnte, wäre das Spiel ein reines Glücksspiel. Rein zufälliges Wählen ist aber nicht möglich, da der Mensch sich immer von seinen Gedanken beeinflussen lässt, und somit kommt als psychologisch-taktische Komponente hinzu, dass man versuchen kann, die Verhaltensweise des Gegners einzuschätzen. Beispielsweise nimmt ein Spieler nicht gern zweimal dasselbe Symbol hintereinander oder hat eine gewisse Präferenz für eines der Symbole. Um also seine eigene Gewinnchance zu erhöhen, muss man verhindern, dass der Gegner die eigene Wahl erahnen kann, er seine Figuren also zufällig auswählen muss. Wenn er jetzt also meint, die Figuren des Gegners erahnen zu können (er könnte zum Beispiel denken, dass der Gegner, nachdem er bereits dreimal Stein gewählt hat, das auch noch ein viertes Mal macht) und er sich darauf einstellt, indem er diesmal Papier wählt, rückt er vom Zufall ab. Dadurch wird er angreifbar, da der Gegner damit rechnen könnte und statt des vierten Mals Stein die Schere wählt.[1] Professionelle Spieler legen deshalb vor den Turnieren ihre Reihenfolge der Figuren fest und merken sich diese Listen, sogenannte Gambits, die sie dann im Turnier durchspielen.
Rein statistisch gesehen wird die Schere bei der „Schere, Stein, Papier“-Weltmeisterschaft mit 29,6 % am seltensten gewählt.[2]
Nach dem law of effect (Gesetz der (Aus)-Wirkung) von Edward Lee Thorndike neigen Spieler beim Gewinn eher dazu in der nächsten Runde bei der gewählten Spielfigur zu bleiben. Bei einer Niederlage oder bei einem Unentschieden neigen sie zur Wahl einer anderen Spielfigur. Haben Spieler verloren, wählen sie eher die niedrigere Spielfigur zu ihrer vorher gewählten (Papier statt Schere, Stein statt Papier, Schere statt Stein) in der nächsten Runde. Bei einem Unentschieden dagegen entscheiden sich Spieler statistisch für die nächsthöhere Spielfigur (Schere statt Papier, Papier statt Stein, Stein statt Schere) in der nächsten Runde.[3] Nach diesen Erkenntnissen kann man folgende Strategie verfolgen: Nimm nach einem Unentschieden die nächsttiefere Spielfigur, nimm nach einem Sieg die Spielfigur, die der Gegner gewählt hatte, nimm nach einer Niederlage die nächsthöhere Spielfigur als die, die der Gegner gewählt hatte.[4]
Geschichte des Spiels
%252C_Japanese_rock-paper-scissors_variant%252C_from_the_Kensarae_sumai_zue_(1809).jpg.webp)
%252C_Japanese_rock-paper-scissors_variant%252C_from_the_Genyoku_sui_bento_(1774).jpg.webp)
Die Herkunft des Spiels ist nicht vollkommen geklärt. Man nimmt an, dass es über Japan nach Europa gelangt ist.
Das japanische Sansukumi-ken (三すくみ拳) bezeichnet eine Reihe von Trinkspielen, die mit den Händen gespielt wurden. Das „ken“ bezeichnet dabei eine Faust, und verschiedene Varianten sind dazu belegt. Die ältesten Formen werden in das 17. Jahrhundert eingeordnet – dabei gewinnt der Frosch (der Daumen) gegen die Giftschnecke (kleiner Finger), die Giftschnecke gewinnt gegen die Schlange (Zeigefinger), und die Schlange gegen den Frosch. Spiele mit Symbolen für diese Tiere sind auch in älteren chinesischen Texten bekannt, so dass eine Herkunft von dort angenommen wird. Dieses mushi-ken wurde später auch mit anderen Tierbezügen gespielt.
Im Laufe der Zeit wurden andere Spiele nach dem Muster mit drei Gesten entwickelt. Bekannt ist etwa mitsu-ken oder kitsune-ken, das mit beiden Händen gespielt wird. Dabei gewinnt der mythische Fuchs Kitsune gegen den Dorfvorsteher, der Dorfvorsteher gewinnt gegen den Jäger, und der Jäger gewinnt gegen den Fuchs. Schlussendlich ist in Japan auch die einhändige Variante jan-ken mit den Gesten für Schere, Stein, Papier entwickelt worden, das sich wiederum im asiatischen Raum verbreitete, und darüber im 19. Jahrhundert nach Europa gekommen ist.
Auch Schimpansen können „Schere, Stein, Papier“ erlernen.[5]
Erweiterungen
Vier Gesten

Es gibt weitere Varianten mit mehr möglichen Handhaltungen. Dabei werden die Figuren beispielsweise um den Brunnen erweitert. Beim Brunnen bildet der Daumen mit den restlichen Fingern einen Kreis. Wird von einem Spieler der Brunnen gewählt, so gewinnt er gegen den Stein und die Schere, die beide in den Brunnen fallen, verliert aber gegen das Papier, das den Brunnen abdeckt.
Dadurch, dass das Spiel um die Figur Brunnen erweitert wurde, verschiebt sich das Gleichgewicht der Gewinnchancen. Wenn es nun vier erlaubte Symbole gibt, kann die Gewinnchance nicht mehr bei allen gleich groß sein, da jede Figur gegen drei andere ein Ergebnis bekommt, anstatt gegen zwei, wie bei der Variante ohne Brunnen.
| Stein | Schere | Papier | Brunnen | |
|---|---|---|---|---|
| Stein | X | + | − | − |
| Schere | − | X | + | − |
| Papier | + | − | X | + |
| Brunnen | + | + | − | X |
- Die Tabelle der möglichen Handzeichen, erweitert um die Figur Brunnen. Von links nach rechts gelesen, bedeutet ein Plus, dass die Figur gewinnt, ein Minus bedeutet, dass sie verliert, und das X , dass das Spiel unentschieden endet.
Betrachtet man nun in dieser Darstellung die Wertigkeit der Figuren zueinander, fällt auf, dass die Figuren Papier und Brunnen jeweils zweimal gewinnen und nur einmal verlieren. Vergleicht man den Stein und den Brunnen, fällt auf, dass sie beide gegen das Papier verlieren und gegen die Schere gewinnen, im direkten Vergleich der Stein aber den Kürzeren zieht. Brunnen ist also gegen kein Symbol schlechter als Stein, dafür aber zweimal besser. Spieltheoretisch ist Brunnen eine zu Stein dominante Strategie. Wenn man schwach dominierte Strategien eliminiert, also wenn der Stein nicht mehr gewählt werden würde, hätte man wieder die Ausgangssituation, in der jede Figur einmal gegen jede andere gewinnt und verliert (siehe Tabelle unten, in der die Strategie Stein eliminiert wurde und sich ein zur Ausgangssituation Stein-Schere-Papier äquivalentes Spiel einstellt).
| Schere | Papier | Brunnen | |
|---|---|---|---|
| Schere | X | + | − |
| Papier | − | X | + |
| Brunnen | + | − | X |
- Der Stein wurde durch den Brunnen ersetzt, ansonsten ändert sich für den Spieler nichts. Jede Figur schlägt einmal jede und wird auch einmal geschlagen.
- Damit das Spiel mit vier Symbolen trotzdem sinnvoll gespielt werden kann, muss das dominierte Symbol (Stein) im Erfolgsfall (gegen Schere) höher gewertet werden (beispielsweise als Doppelsieg).
Fünf Gesten
Bei dieser Erweiterung gibt es fünf Symbole und es gibt wie bei der Grundversion keine „besseren“ Symbole. Die Wahrscheinlichkeit für gleiche Symbole sinkt dagegen.
Das Streichholz wird mit einem ausgestreckten Zeigefinger dargestellt. Es verbrennt das Papier und schwimmt im Brunnen, gewinnt also. Es wird aber vom Stein zerschlagen und von der Schere zerschnitten, wobei es verliert. Insgesamt ergibt sich:
| Stein | Schere | Papier | Brunnen | Streichholz | |
|---|---|---|---|---|---|
| Stein | X | + | − | − | + |
| Schere | − | X | + | − | + |
| Papier | + | − | X | + | − |
| Brunnen | + | + | − | X | − |
| Streichholz | − | − | + | + | X |
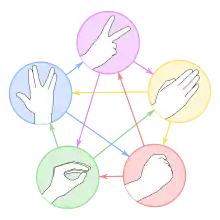
Eine durch die Serie The Big Bang Theory bekannt gewordene Variante davon ist Stein–Papier–Schere–Echse–Spock (engl. Rock–Paper–Scissors–Lizard–Spock), bei der anstatt Streichholz und Brunnen Echse und Mr. Spock eingesetzt werden: Schere schneidet Papier, Papier bedeckt Stein, Stein zerquetscht Echse, Echse vergiftet Spock, Spock zertrümmert Schere, Schere köpft Echse, Echse frisst Papier, Papier widerlegt Spock, Spock verdampft Stein, und Stein schleift Schere. Diese Variante wurde vom Amerikaner Sam Kass zusammen mit Karen Bryla erfunden.[6]
Andere Erweiterungen
Das Spiel kann durch weitere Handzeichen ergänzt werden. Die Erweiterung durch viele weitere Figuren erschwert das Spiel und damit die Spielbarkeit. Der Nutzen wird manchmal damit erklärt, dass es weniger wahrscheinlich ist, zwei gleiche Symbole zu zeigen und damit ein Unentschieden zu produzieren.
Modifikationen und Sonderformen

Neben der wohl bekanntesten Änderung, der oben angesprochenen Ergänzung durch den Brunnen, gibt es oft auch noch mehr Ergänzungen durch Symbole wie Feuer oder Ähnliches. Oft wird das Spiel so gespielt, dass erst der eine Runde gewonnen hat, der zuerst drei Punkte oder mehr erreicht hat. Es gibt auch Varianten, bei denen der Sprechrhythmus nicht aus dem Takt geraten darf und man nach jeder verlorenen Runde mit einem körperlichen Manko (beispielsweise auf einem Bein) weiterspielen muss oder bei dem man nach einer Niederlage ein Kleidungsstück ausziehen muss.
Japanische Gewinnermittlung
In einer weit verbreiteten japanischen Variante des Spiels ist bei einer Überlegenheit einer Geste noch keineswegs die Runde gewonnen. Dazu muss man noch die Blickrichtung erraten, in die der Unterlegene beim dritten Akzent einer ebenfalls rhythmisch gesprochenen Strophe schauen wird. Dafür hält der vermeintliche Gewinner seinen Zeigefinger vor die Nasenspitze des Mitspielers und spricht im selben Takt wie zuvor die Silben „Atchi-Muite-Hoi“. Auf „Hoi“ müssen sich beide Spieler gleichzeitig für eine Richtung entscheiden, also oben, unten, rechts oder links. Der Unterlegene der Vorrunde muss auf der Silbe „Hoi“ ruckartig seinen Kopf in eine der vier Richtungen drehen, der mögliche Gewinner zeigt mit seinem Zeigefinger in eine spontan gewählte Richtung. Erst bei einer Übereinstimmung geht ein Siegpunkt an den Gewinner, andernfalls gilt auch die als „Jan-Ken-Pon“ übliche Vorrunde (nur Stein, Schere, Papier) als unentschieden. Oft kann man die Niederlage so noch aufhalten.
Mora/Morra
Insbesondere in Italien, aber auch in anderen südlichen Ländern ist das Fingerspiel Morra oder Mora bekannt. Obwohl das Spiel nicht aus Schere, Stein, Papier hervorgeht, gibt es doch gewisse Ähnlichkeiten. Bei diesem Spiel entscheiden sich beide Spieler, wie viele Finger einer Hand sie dem Gegner zeigen, und versuchen gleichzeitig die Gesamtanzahl der Finger zu erraten. Wer die richtige Gesamtanzahl der von beiden gezeigten Finger gerufen hat, hat das Spiel gewonnen und bekommt einen Punkt. Ähnlich wie bei Schere, Stein, Papier wird auch hier gespielt, bis einer der beiden Spieler eine vereinbarte Gesamtpunktzahl erreicht hat.
Gerade und Ungerade
Das bereits im antiken Griechenland und Rom bekannte Gerade und Ungerade ist ein einfaches Glücksspiel, welches darin besteht, dass man verschiedene Münzen oder sonstige kleine Gegenstände in die Hand nimmt, diese schließt und einen anderen erraten lässt, ob die Anzahl der Gegenstände eine gerade oder ungerade sei.
Bei der Version, die Morra sehr ähnelt, entscheiden sich ebenfalls beide Spieler, wie viele Finger einer Hand sie dem Gegner zeigen. Da vorher festgelegt wurde, wer bei Gerade und wer bei Ungerade gewinnt, liegt der Reiz bei dieser Variante darin, die vom Gegner vermutete Anzahl der Finger so mit der eigenen Anzahl zu kombinieren, dass am Ende die zuvor festgelegte Zuordnung von Gerade oder Ungerade erreicht wird. Wer eine Übereinstimmung mit der zuvor festgelegten Zuordnung erreicht hat, bekommt einen Punkt. Bei dieser Variante des Fingerspiels gibt es also nie ein Unentschieden.
Schere-Stein-Papier-Prinzip
Bisweilen ist von dem „Schere-Stein-Papier-Prinzip“ die Rede, meist im Zusammenhang mit Strategiespielen. Damit ist gemeint, dass eine Kampfeinheit bestimmten Einheiten überlegen ist, anderen hingegen unterlegen, ohne dass diese generell zu schwach oder zu stark wären. Dieses Prinzip sorgt dafür, dass strategische Planung angewandt werden muss, um die Schwächen einer Einheit durch eine andere zu kompensieren, und ermöglicht durch die entstehende Einheitenvielfalt verschiedene taktische Manöver; es ist heute daher Teil der meisten Duell- und Strategiespiele. Beispiel: Infanterie gewinnt gegen Kavallerie, Bogenschützen gegen Infanterie und Kavallerie gegen Bogenschützen.
Mathematisch betrachtet handelt es sich beim „Schere-Stein-Papier-Prinzip“ um eine intransitive Relation.
Literatur
- Benjamin James Dyson, Jonathan Michael Paul Wilbiks, Raj Sandhu, Georgios Papanicolaou, Jaimie Lintag: Negative outcomes evoke cyclic irrational decisions in Rock, Paper, Scissors, Scientific Reports 6, Article number: 20479 (2016), doi:10.1038/srep20479
- Zhijian Wang, Bin Xu, Hai-Jun Zhou: Social cycling and conditional responses in the Rock-Paper-Scissors game, Scientific Reports 4, Article number: 5830 (2014), doi:10.1038/srep05830
- Christian Rieck: Spieltheorie. 5. Auflage. Rieck Verlag, ISBN 3-924043-91-4
- Sepp Linhart: Rituality in the ken game. In: Jan van Bremen, D. P. Martinez: Ceremony and Ritual in Japan. Religious Practices in an Industrialized Society. Routledge, London & New York 1995, ISBN 0-415-11663-5. S. 38–66
- Douglas Walker, Graham Walker: The Official Rock Paper Scissors Strategy Guide. Fireside Books (Simon & Schuster), New York 2004, ISBN 978-0-7432-6751-9
Weblinks
Einzelnachweise
- http://www.neues-deutschland.de/artikel/961736.poker-per-fingerzeig.html?sstr=Poker%7Cper%7CFingerzeig
- World RPS Society: How to beat someone at Rock, Paper, Scissors, abgerufen am 17. Oktober 2017
- Wang (2014), Dyson (2016)
- Teresa Nauber: Wie Sie bei Schnick-Schnack-Schnuck öfter gewinnen, Die Welt, 20. April 2016
- Jie Gao, Yanjie Su, Masaki Tomonaga, Tetsuro Matsuzawa (2017) Learning the rules of the rock–paper–scissors game: chimpanzees versus children. In: Primates, doi:10.1007/s10329-017-0620-0
- Sam Kass: Rock Paper Scissors Spock Lizard.