Punktmechanik

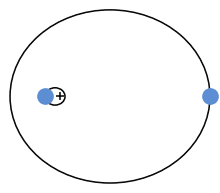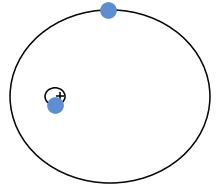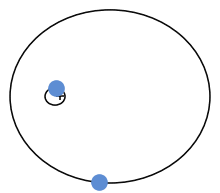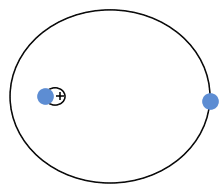
Die Punktmechanik[1][2]^{:66 ff., 77–166}[3] ist ein Teilgebiet der Mechanik, in dem von der Beschaffenheit und Gestalt der Körper, deren Bewegungen interessieren, abgesehen wird und sie auf ihre im Massenmittelpunkt konzentrierte Masse reduziert werden. Diese Idealisierung vereinfacht die mathematische Behandlung und hatte ihre ersten Erfolge in der Himmelsmechanik, wo es Isaac Newton gelang, die Keplerbahnen um die Sonne mathematisch darzustellen (siehe Bild). Denn die Abmessungen der Himmelskörper sind im Sonnensystem klein gegen ihren Abstand und der Einfluss der Eigenrotationen ist vernachlässigbar.[4]

Zweikörperproblem von zwei sich anziehenden Massenpunkten (blau)

In vielen Bereichen und Anwendungen ist das Konzept des Massenpunkts erfolgreich und es können mit ihm auch Aspekte der Relativitätstheorie und Quantenmechanik behandelt werden. Die Darstellung bleibt dabei aber übersichtlich und auch Anfängern zugänglich.[1]^{:V ff.}

Geschichtliches

Die Punktmechanik geht auf den Begründer der theoretischen Physik Isaac Newton zurück. Ihm gelang es, aus den Kepler’schen Gesetzen das Gravitationsgesetz herzuleiten[5]^{:494, 498} und den Flächensatz auf beliebige Zentralkräfte zu verallgemeinern.[5]^:464 Dieser Erfolg führte zum Bemühen alle Naturerscheinungen auf Kräfte zurückzuführen, die zwischen zwei punktförmigen Teilchen wirken und nur von deren Abstand abhängen, eine Auffassung, die die Physik bis weit ins 19. Jahrhundert beherrschte.[5]^:449

Eine neue Anwendung hat die Punktdynamik darin gefunden, mechanische Analogien physikalischer Erscheinungen zu liefern, mit denen beispielsweise James Clerk Maxwell zu seinen Fundamentalgleichungen des Elektromagnetismus gelangte. Die Bewegungsgleichungen können vom mechanischen System auf das analoge übertragen werden, wodurch die Lagrangegleichungen eine universelle Bedeutung für die ganze Physik gewannen.[5]^{:451 ff.}

Mechanisch ähnliches Verhalten von Systemen fiel schon Aristoteles, Galileo Galilei und Isaac Newton auf aber erst M. J. Bertrand hat das Prinzip der mechanischen Ähnlichkeit von der Punktmechanik ausgehend in voller Strenge ausgesprochen.[5]^:478[6]

Anwendungsbereiche und Limitierungen

Die Idealisierung eines Körpers als Massenpunkt ist probat, wenn eine charakteristische Abmessung des Körpers klein ist gegen die Genauigkeit, mit der Längenmessungen vorgenommen werden,[1]^{:1 f.} und Fehler in der Größenordnung des Verhältnisses der gleich null gesetzten Strecken zu den anderen Strecken in kauf genommen werden können.[2]^{:66 f.} Der Ort des Massenpunkts ist im Allgemeinen der Massenmittelpunkt oder – was oft dasselbe ist – der Schwerpunkt des von ihm repräsentierten Körpers.

Effekte, die auf die Ausdehnung realer Körper zurückgehen, kann die Punktmechanik nicht behandeln. Eigendrehung mit Präzession und Nutation oder Verformungen können zutreffender mit anderen Disziplinen wie Starrkörper- oder Kontinuumsmechanik abgebildet werden, wo die Mathematik jedoch ungleich komplizierter ist, nicht zuletzt, weil der Starrkörper sechs und der verformbare unendlich viele Freiheitsgrade besitzt.[4] Die Bedeutung des Drallsatzes als unabhängiges Prinzip ist in der Punktmechanik nicht darstellbar, siehe Drallsatz in der Punktmechanik, denn in der Punktmechanik ist die Drehimpulserhaltung eine Konsequenz der Impulserhaltung und davon, dass Massenpunkte nur Zentralkräfte aufnehmen können.

Seit der Begründung der theoretischen Physik durch Isaac Newton 1687 wird die elementare Punktmechanik in den Lehrbüchern praktisch unverändert dargestellt, und das obwohl sie in mancher Hinsicht logisch unbefriedigend ist. Diese Mängel in der Newton’schen Mechanik wurden durch die Relativitätstheorie und Quantenmechanik behoben, doch es gibt eine beträchtliche Anzahl von Aussagen, die in der klassischen und der modernen Physik gleich lauten. Diese Aussagen betreffen sämtlich fundamentale physikalische Größen, die Prozesse durch ihren Austausch beschreiben. So ist der Newton’schen, Einstein’schen und der Quantenmechanik gemeinsam, dass zusammenstoßende Körper oder Teilchen Impuls und Energie austauschen. Nur die Kinematik, also die geometrische Darstellung der Bewegung durch den Raum, ist in der modernen Physik und der klassischen Mechanik grundverschieden.[1]^{:V ff.}

Bewegungsgleichungen und Integrale der Bewegung

Die Bewegung eines Massenpunkts wird durch seinen dreidimensionalen Ortsvektor als Funktion des Zeitparameters beschrieben, der wie eine zusätzliche Koordinate behandelt wird. Während der Massenpunkt durch den Raum wandert, kann durch Zeitableitungen seine Geschwindigkeit und Beschleunigung ermittelt werden. In physikalischen Gesetzen wie Newton’s Gravitationsgesetz oder dem Coulomb-Gesetz ist umgekehrt die Beschleunigung des Massenpunkts vorgegeben und das Weg-Zeit-Gesetz ergibt sich dann durch zweifache Zeitintegration. Eine Schar von Bahnkurven kennzeichnen den zum Beschleunigungsverlauf gehörigen Bewegungstyp.[1]^:10 So sind die Keplerbahnen der Bewegungstyp der Planeten im Gravitationsfeld des Sonnensystems.

Von Bedeutung sind Größen, die für einen sich bahntypisch bewegenden Körper über die Zeit konstant sind. Diese Konstanten werden Integrale der Bewegung oder erste Integrale eines Bewegungstyps genannt und haben in den Erhaltungssätzen fundamentale Vertreter. Beispielsweise ist die Gesamtenergie eines isolierten Systems von Massenpunkten aufgrund des Energieerhaltungssatzes ein Integral der Bewegung. Aus den ersten Integralen lassen sich häufig wichtige Schlüsse über den Verlauf der Bewegung ziehen, siehe beispielsweise den folgenden Abschnitt #Newton’s Gravitationsgesetz. Die Integrale sind eine Funktion des Ortes und der Geschwindigkeit aber entlang der Bahnkurve konstant, weswegen der Funktionswert schon mit den Anfangsbedingungen festliegt.[1]^:18

Newton’s Gravitationsgesetz

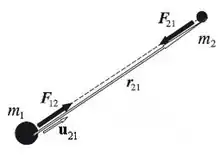
Zwei sich anziehende Massenpunkte m₁ und m₂

Das Newton’sche Gravitationsgesetz besagt, dass zwei wechselwirkende Massenpunkte aufeinander zu beschleunigt werden, was sich als Anziehungskraft bemerkbar macht, siehe Bild. In moderner Sichtweise ist das Gravitationsfeld ein Beschleunigungsfeld und kein Kraftfeld.[1]^:22 Newton hatte aus den Kepler’schen Gesetzen sein Gravitationsgesetz hergeleitet und Johann I Bernoulli konnte 1710 zeigen, dass eine dem Quadrat des Abstands reziproke Zentralkraft wie bei Newtons Gesetz stets zu einer Keplerbewegung auf einem Kegelschnitt führt.[5]^:494

Der Bewegungstyp der Newton’schen Gravitationstheorie sind dementsprechend Keplerbahnen, wie sie Himmelskörper verfolgen. Das Bewegungsintegral in Form der spezifischen Bahnenergie bestimmt den Bewegungstyp, der ellipsen-, hyperbel- oder parabelförmig ist, je nachdem das Integral negativ, positiv oder null ist. Das Zweikörperproblem kann analytisch gelöst werden,[1]^{:23 ff.} was beim Dreikörperproblem und N-Körper-Problem mit N > 3 im Allgemeinen nicht (analytisch) möglich ist.

Bei gravitativ wechselwirkenden Massenpunkten existieren sieben Integrale der Bewegung, die auf die Erhaltungssätze von Impuls, Drehimpuls und Energie zurückgehen. Am Impuls- und Energieaustausch zwischen den Körpern beteiligt sich auch das von ihnen erzeugte Gravitationsfeld, das im Gegensatz zu den Massenpunkten nicht lokalisierbar, sondern über den gesamten Raum ausgebreitet ist. Das Newton’sche Gravitationsfeld kann Energie aufnehmen, nicht aber Impuls, den es deshalb unverzüglich an andere Massenpunkte wieder abgibt (Prinzip Actio und Reactio).[1]^:75

Die im Zweikörpersystem des Zweikörperproblems gespeicherte, konstante Gesamtenergie kann aufgespalten werden in die Schwerpunkts- oder äußere Energie, die die konstante kinetische Energie des Schwerpunkts ist, und die daher ebenfalls konstante innere Energie. Die Schwerpunktsenergie kann durch Übergang ins Schwerpunktsystem, in dem der Gesamtimpuls verschwindet, auf null reduziert werden, während die innere Energie invariant gegen Galilei-Transformationen ist. In Abwesenheit von Gesamtimpuls ist die Gesamtenergie minimal und gleicht der inneren Energie. Mit dieser Zerlegung vereinfacht sich die Lösung des Zweikörperproblems. Die Aufspaltung in wegtransformierbare äußere Energie und einen Minimalwert der Energie, die innere oder Ruheenergie, ist auch in der Einstein’schen Mechanik von Bedeutung.[1]^:73

Dynamik

Die Dynamik beschreibt die Bewegung eines Körpers so, dass der Körper im Lauf der Bewegung bestimmte austauschbare physikalische Größen von anderen Körpern oder Systemen aufnimmt oder an diese abgibt. In der Punktmechanik sind Impuls, Drehimpuls und Energie austauschbar und für sie gelten Erhaltungssätze (Impulserhaltungssatz, Drehimpulserhaltungssatz, Energieerhaltungssatz). Sie können daher weder erzeugt noch vernichtet, sondern nur aufgenommen, abgegeben oder behalten werden. Das Gravitationsfeld beteiligt sich an dem Austausch und vermag Impuls und Energie von einem Körper auf andere zu übertragen.[1]^:76

Impulsbilanz

Zwei Massenpunkte können Impuls durch Kräfte übertragen, die sie nach dem Prinzip Actio und Reactio immer paarweise entgegengesetzt gleich aufeinander ausüben, wie beispielsweise beim Zusammenstoß. Die modellierten realen Körper verformen sich dabei mehr oder weniger, worin sich die gegenseitigen Kraftwirkungen offenbaren. Die Impulsübertragung geschieht nach Newton’s zweitem Gesetz Kraft gleich Masse mal Beschleunigung, wo das Produkt aus Masse und Beschleunigung die Impulsänderungsgeschwindigkeit ist. Die Impulszu- oder -abnahme ist das Resultat des ausgeübten Kraftstoßes, durch den das ausübende System in gleichem Maß Impuls verliert, wie es durch den Kraftstoß überträgt. Auch das Gravitationsfeld vermag durch die Anziehungskraft eine Impulsänderung zu bewirken, da es aber selbst keinen Impuls aufnehmen kann, muss es ihn momentan an andere Massenpunkte abgeben (Prinzip Actio und Reactio). Jean-Baptiste le Rond d’Alembert sah im Produkt aus Masse und Beschleunigung die „Trägheitskraft“ und in der Gravitationskraft eine „äußere Kraft“.[1]^{:70 f.} Davon zu unterscheiden ist die Reaktionskraft aufgrund von geometrischen Bindungen an Schienen oder Flächen, eine Kraft, die sich erst im Bewegungsverlauf ergibt.

Drehimpulsbilanz

Der Drehimpuls ist wie der Impuls eine Erhaltungsgröße und kann nur verändert werden, indem ein Drehmoment aufgebracht wird. Dem System, das das Drehmoment ausübt, wird in gleichem Maß Drehimpuls entzogen, wie dieser durch das Moment übertragen wird.

Bei einem System von Massenpunkten kann der Drehimpuls zerlegt werden in den Bahndrehimpuls des Massenmittelpunkts und einen Eigendrehimpuls um den Massenmittelpunkt. Beide Drehimpulse, Bahn- und Eigendrehimpuls, sind Erhaltungsgrößen aber nur der Eigendrehimpuls ist invariant gegen Galilei-Transformationen des Bezugssystems. Zwei nicht rotierende, gegeneinander gleichförmig bewegte Beobachter nehmen immer übereinstimmende Eigendrehimpulse der von ihnen beobachteten Körper wahr.[1]^:102

Energiebilanz

Die Energie eines Massenpunkts kann nur verändert werden, indem eine Kraft an ihm Arbeit entlang eines Weges verrichtet. Das die Kraft ausübende System verliert dabei in gleichem Maß an Energie, wie durch die Arbeit übertragen wird. Die Geschwindigkeit der Energieübertragung ist die Arbeit pro Zeiteinheit oder die Leistung. Relativ zu einem festen Bezugspunkt bringt die Kraft ein Drehmoment auf, das Arbeit bei der Drehung verrichtet, sodass dem Massenpunkt Rotationsenergie verliehen wird.

Das Gravitationsfeld vermag Lageenergie von Massenpunkten aufzunehmen, zu speichern oder an sie abzugeben.

Massenerhaltung

Mit dem Impuls muss in der Newton’schen Dynamik auch die Masse einen Erhaltungssatz erfüllen.

Denn der Gesamtimpuls eines abgeschlossenen Systems von Massenpunkten ist, anders als deren Massen, abhängig von der Geschwindigkeit des benutzten Bezugssystems. Im Schwerpunktssystem ist der Gesamtimpuls konstant null, auch wenn die Massenpunkte untereinander Impuls austauschen. Ein relativ dazu gleichförmig bewegter Beobachter stellt ein zu seiner Relativgeschwindigkeit und der Gesamtmasse proportionalen, ebenfalls konstanten Gesamtimpuls wahr. Weil das bei jeder Relativgeschwindigkeit festzustellen ist, muss die Gesamtmasse zu jeder Zeit dieselbe sein. Dies gilt auch dann, wenn eine Geschwindigkeitsabhängigkeit der Einzelmassen zugelassen wird.[1]^:80

In der Newton’schen Mechanik sind schwere Masse und träge Masse zwangsweise proportional zueinander.

Denn beim Zweikörperproblem geht in das Impulsintegral der Bewegung nur die schwere Masse („Gravitationsladung“) und ihre momentane Geschwindigkeit ein. Dieselben Körper würden bei einem Zusammenstoß mit derselben Geschwindigkeit einen zu ihrer trägen Masse proportionalen Impuls zeigen, der in Summe ebenfalls eine Erhaltungsgröße ist. In den Impulsgleichungen treten die Geschwindigkeiten mit den schweren bzw. trägen Massen als Koeffizienten auf. Wären beide Gleichungen linear unabhängig, könnten aus ihnen die dann zwangsläufig konstanten Geschwindigkeiten berechnet werden und wären somit nur geradlinige Bewegungen auf den Keplerbahnen erlaubt, was offensichtlich nicht zutrifft. Lineare Abhängigkeit der Gleichungen mündet in die Proportionalität der trägen und schweren Massen in der Newton’schen Mechanik.[1]^:73

Aspekte der modernen Physik

Grundlagen der Mechanik

Die Newton’sche und Einstein’sche Mechanik können aus drei Gesetzen abgeleitet werden:

Impuls und Energie sind Erhaltungsgrößen.[1]^:66
Geschwindigkeit ${\vec {v}}$ und Impuls ${\vec {p}}$ sind parallel und ihr Proportionalitätsfaktor, die Masse $m$ , kann von der Geschwindigkeit abhängen:[1]^:67 ${\vec {p}}=m(v){\vec {v}}$
Fundamentalgleichung der Dynamik: Die Änderung der Energie dE entspricht der Änderung des Impulses $\mathrm {d} {\vec {p}}$ , wenn die Transportgeschwindigkeit der Energie gleich der Geschwindigkeit ist:[1]^:76 $\mathrm {d} E={\vec {v}}\cdot \mathrm {d} {\vec {p}}$ .

Eine Mechanik wird durch die Energie-Impuls-Relation $E=E({\vec {p}})$ definiert.[1]^:79

Newton’sche Mechanik

In der Newton’schen Mechanik ist ${\vec {p}}=m{\vec {v}}$ , die Masse m konstant und $\mathrm {d} E={\tfrac {1}{m}}{\vec {p}}\cdot \mathrm {d} {\vec {p}}={\tfrac {1}{m}}\mathrm {d} (p^{2}/2)$ , woraus sich die Energie-Impuls-Relation[1]^:77

E({\vec {p}})={\frac {p^{2}}{2m}}+E_{0}={\frac {m}{2}}v^{2}+E_{0}

ableitet. Die Konstante $E_{0}$ ist die innere Energie bei ${\vec {p}}={\vec {0}}$ .

Einstein’sche Mechanik

In der Einstein’schen Mechanik ist $E=c^{2}m(v)$ mit der Lichtgeschwindigkeit c und aus der Geschwindigkeits-Impuls-Relation (2) und der Fundamentalgleichung (3) ergibt sich:[1]^{:81 f.}

\mathrm {d} E={\vec {v}}\cdot \mathrm {d} {\vec {p}}={\frac {c^{2}}{E}}{\vec {p}}\cdot \mathrm {d} {\vec {p}}={\frac {c^{2}}{E}}\mathrm {d} (p^{2}/2)

oder $E^{2}=(cp)^{2}+E_{0}^{2}$ , wo $E_{0}$ die Ruheenergie ist. Einsetzen von Impuls und Energie als Funktion der Masse ergibt

E={\frac {E_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}

und

m(v)={\frac {\frac {E_{0}}{c^{2}}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}

Die Beziehung zwischen Geschwindigkeit und Impuls (2) führt auf den relativistischen Impuls, womit dann klar ist, dass sich Geschwindigkeiten nicht mehr so einfach wie in der Newton’schen Mechanik addieren. Aus der Betrachtung eines zerfallenden Teilchens leitet sich das relativistische Additionstheorem für Geschwindigkeiten ab.[1]^:84

In der Relativitätstheorie ist jeder Austausch durch die Lichtgeschwindigkeit begrenzt. Während das Gravitationsfeld zum Beispiel Impuls von einem Massenpunkt auf den anderen überträgt, kann der Impulserhaltungssatz verletzt erscheinen, denn der zu übertragende Teil des Impulses ist im Feld absorbiert, was als Retardierung bekannt ist, siehe auch Retardiertes Potential im Elektromagnetismus.

Der Energieerhaltungssatz der Einstein’schen Mechanik zerfällt im Grenzfall kleiner Geschwindigkeiten in einen Erhaltungssatz für die innere Energie und einen für die Masse[1]^:87. Ganz allgemein enthält die Einstein’sche Mechanik die Newton’sche als Grenzfall bei kleinen Energien und Impulsen.

Quantenmechanik

Feynmandiagramm für den Zerfall eines Neutrons n in Proton p, Elektron e⁻ und Elektron-Antineutrino

{\overline {\nu }}_{e}

vermittelt über ein W-Boson W⁻.

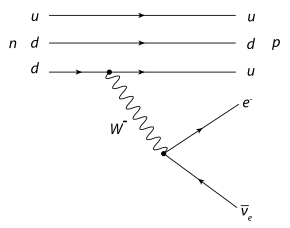
In der Quantenmechanik kann auch mit Massenpunkten gearbeitet werden,[1]^:97 wenn ihnen neben Impuls, Energie und/oder Masse auch ein Eigendrehimpuls in Form eines Spin und andere Größen wie Ladung zugeordnet werden. Diese physikalischen Größen können in der Quantenmechanik nur diskrete Werte annehmen und unterliegen ebenfalls Erhaltungssätzen.[1]^:114 Aus der Drehimpulserhaltung ist beispielsweise erkennbar, das beim β^–-Zerfall des Neutrons in ein Proton und ein Elektron mit jeweils gleichem Spin ℏ/2, trotzdem die Ladungserhaltung durch die drei Teilchen bereits gewährleistet ist, noch ein viertes Teilchen mit Spin ℏ/2 entstehen muss, siehe Bild.[1]^{:105 f.}

Siehe auch

Anwendungen: Ballistik, Mathematisches Pendel, Foucaultsches Pendel
Bahnkurven: Wurfparabel, Brachistochrone, Traktrix
Statistische Mechanik

Weblinks

Wagner, Paul: Einführung in die Physik I, II Mechanik: Dynamik von Massenpunkten. Technische Informationsbibliothek, 2015, abgerufen am 26. Februar 2020.

Literatur

Gottfried Falk: Theoretische Physik auf der Grundlage einer allgemeinen Dynamik. Elementare Punktmechanik. 1. Band. Springer-Verlag, Berlin, Heidelberg 1966, DNB 456597212, doi:10.1007/978-3-642-94958-6.
Georg Hamel: Elementare Mechanik. Ein Lehrbuch. B. G. Teubner, Leipzig und Berlin 1912, S. 66 f. (archive.org [abgerufen am 26. Februar 2020]).
Punktmechanik. Spektrumverlag, 1998, abgerufen am 26. Februar 2020.
Wilderich Tuschmann, Peter Hawig: Sofia Kowalewskaja. Ein Leben für Mathematik und Emanzipation. Birkhäuser Verlag, Basel 1993, ISBN 978-3-0348-5721-5, S. 119 f., doi:10.1007/978-3-0348-5720-8 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 25. Mai 2017]).
Paul Stäckel, redigiert von Felix Klein und Conr. Müller: Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Mechanik. Hrsg.: Akademien der Wissenschaften zu Göttingen, Leipzig, München und Wien. Vierter Band, 1. Teilband, Art. 6.1: Punktdynamik. B. G. Teubner Verlag, 1908, ISBN 978-3-663-16021-2, S. 449 ff., doi:10.1007/978-3-663-16021-2 (wikisource.org [abgerufen am 24. Januar 2020]).
J. M. Bertrand: Notiz über die Ähnlichkeit in der Mechanik. In: École polytechnique (Hrsg.): Journal de l’École polytechnique. Tome XIX, Nr. 32. Bachelier, Paris 1848, S. 189–197 (französisch, bnf.fr [abgerufen am 28. Februar 2020] Originaltitel: Note sur la similitude en méchanique.).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[falk-1] Gottfried Falk: Theoretische Physik auf der Grundlage einer allgemeinen Dynamik. Elementare Punktmechanik. 1. Band. Springer-Verlag, Berlin, Heidelberg 1966, DNB 456597212, doi:10.1007/978-3-642-94958-6.

[hamel-2] Georg Hamel: Elementare Mechanik. Ein Lehrbuch. B. G. Teubner, Leipzig und Berlin 1912, S. 66 f. (archive.org [abgerufen am 26. Februar 2020]).

[3] Punktmechanik. Spektrumverlag, 1998, abgerufen am 26. Februar 2020.

[Tuschmann-4] Wilderich Tuschmann, Peter Hawig: Sofia Kowalewskaja. Ein Leben für Mathematik und Emanzipation. Birkhäuser Verlag, Basel 1993, ISBN 978-3-0348-5721-5, S. 119 f., doi:10.1007/978-3-0348-5720-8 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 25. Mai 2017]).

[staeckel-5] Paul Stäckel, redigiert von Felix Klein und Conr. Müller: Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Mechanik. Hrsg.: Akademien der Wissenschaften zu Göttingen, Leipzig, München und Wien. Vierter Band, 1. Teilband, Art. 6.1: Punktdynamik. B. G. Teubner Verlag, 1908, ISBN 978-3-663-16021-2, S. 449 ff., doi:10.1007/978-3-663-16021-2 (wikisource.org [abgerufen am 24. Januar 2020]).

[6] J. M. Bertrand: Notiz über die Ähnlichkeit in der Mechanik. In: École polytechnique (Hrsg.): Journal de l’École polytechnique. Tome XIX, Nr. 32. Bachelier, Paris 1848, S. 189–197 (französisch, bnf.fr [abgerufen am 28. Februar 2020] Originaltitel: Note sur la similitude en méchanique.).