Bloch-Wand
Als Bloch-Wand oder blochsche Wand (nach dem schweizerisch-amerikanischen Physiker Felix Bloch) bezeichnet man in ferromagnetischem Material einen Übergangsbereich zwischen den Weiss-Bezirken unterhalb der Curie-Temperatur, in dem sich die Orientierung der magnetischen Momente so ändert, dass sie mit zunehmendem Abstand (~ x) zum Weiss-Bezirk mehr und mehr in der Wandebene verdreht sind; dadurch weisen sie genau in der Mitte zwischen den Weiss-Bezirken nicht in die gleiche Richtung wie in den Weiss-Bezirken (also z. B. in die +y- bzw. -y-Richtung), sondern in die Vertikalrichtung (~ z).
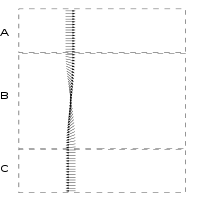
(Die Länge der eingezeichneten Vektorpfeile soll konstant sein.)
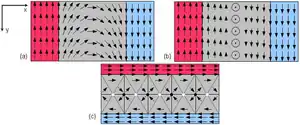
im Vergleich zur Néel-Wand a)
(Darstellung gegenüber der ersten Abb. um 90° gegen den Uhrzeigersinn gedreht)
Erfolgt der Übergang hingegen so, dass die magnetischen Momente auch im Übergangsbereich in der Horizontalebene verbleiben, also in der x-y-Ebene, so spricht man von einer Néel-Wand. Diese kommt, wie dem unten angegebenen Kompendium von A. Hubert und R. Schäfer entnommen werden kann, seltener vor als die Bloch-Wand, außer in dünnen Schichten und speziellen Situationen.
Beschreibung
In der ersten Graphik stellt die (nicht eingezeichnete) zentrale Vertikalebene durch B die eigentliche Ebene der Bloch-Wand dar. Die Magnetisierung ist hier nach oben gerichtet (M ~ z), während sie in den Gebieten A bzw. C gleichförmig nach rechts bzw. links zeigt (M ~ +y bzw. ~ -y). Die eigentliche Blochwand ist nur „ungefähr“ definiert; z. B. kann man dazu das gesamte Zwischengebiet B zählen, mit Ausnahme ganz schmaler Streifen an den beiden eingezeichneten Grenzlinien, wo die Winkelabweichung vom Grenzwert einen sehr kleinen, aber endlichen Wert unterschreitet.
Stoßen zwei Weiss-Bezirke mit unterschiedlicher – meist entgegengesetzter – Magnetisierungsrichtung aneinander, so ändert sich diese Richtung in den Bloch-Wänden fließend. Der Grund für den allmählichen Übergang liegt im energetischen Kompromiss zwischen
- der kurzreichweitigen Austauschenergie, die innerhalb eines Weiss-Bezirks die Spins parallel ausrichtet, und
- der langreichweitigen Dipol-Dipol-Wechselwirkung, die die Spins antiparallel auszurichten versucht.
Die Magnetisierung bleibt dabei – im Gegensatz zur Néel-Wand – immer parallel zur Wandebene, d. h., die Magnetisierung dreht sich helikal. Dadurch zeigt die Magnetisierung der Bloch-Wand an der Materialoberfläche aus der Ebene heraus, und es entsteht ein magnetisches Streufeld, das z. B. über die bitterschen Streifen detektiert werden kann.
Die Größe der Weiss-Bezirke (Domänen) liegt meist unter 100 µm, und die Dicke der Bloch-Wände beträgt meist einige hundert Atomabstände.[1] Die Bloch-Wände wären unendlich dick, wäre nicht die Energie der magnetischen Anisotropie, zu deren Quadratwurzel die Dicke der Bloch-Wände umgekehrt proportional ist:
Die Anisotropieenergie trägt bei, weil die Spins innerhalb der Bloch-Wand zum Großteil in schwere Magnetisierungsrichtungen weisen.
Bloch-Wände werden von Gitterfehlern, Korngrenzen, Einschlüssen oder inneren Spannungen am Ort gehalten. Ein hartmagnetischer Stoff hat viele Gitterfehler und behindert so die Bewegung der Bloch-Wände stark. Durch Anlegen eines äußeren Magnetfelds ändert sich die Position der Bloch-Wände sprunghaft – dies nennt man Barkhausen-Sprünge.
Verallgemeinerungen
Analog spricht man von Bloch-Linien bzw. Bloch-Punkten, wenn von einer Linie bzw. von einem Punkt ausgehend die Magnetisierung in topologisch nichttrivialer Weise von der Richtung abhängt.[2] Andere topologische Verallgemeinerung werden als Skyrmionen bezeichnet.
Literatur
- Hans Fischer: Werkstoffe in der Elektrotechnik. 2. Auflage, Carl Hanser Verlag, München Wien, 1982 ISBN 3-446-13553-7.
- Horst Stöcker: Taschenbuch der Physik. 4. Auflage, Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4.
- Alex Hubert und Rudolf Schäfer: Magnetic Domains, Berlin, Springer 2000, ISBN 3-540-64108-4 (sehr umfangreiches Kompendium)
Einzelnachweise
- Wolfgang Bergmann: Werkstofftechnik 2: Werkstoffherstellung - Werkstoffverarbeitung - Werkstoffanwendung. 3. Auflage. Carl Hanser Verlag, München/Wien 2002, S. 573 (eingeschränkte Vorschau in der Google-Buchsuche).
- W. Döring: Point Singularities in Micromagnetism (Seite nicht mehr abrufbar, Suche in Webarchiven) Info: Der Link wurde automatisch als defekt markiert. Bitte prüfe den Link gemäß Anleitung und entferne dann diesen Hinweis. , J. Appl. Phys. 39, 1006 (1968)