Polbewegung

Als Polbewegung oder Polschwankung (engl. Polar Motion) bezeichnen Astronomen und Geowissenschaftler eine langsame, schwingende Verlagerung der Erdachse innerhalb des Erdkörpers. Sie macht zwar nur einige Millionstel des Erdradius aus, ist aber für die heutige Geowissenschaft – insbesondere Geodäsie und Geophysik – sowie für die Astronomie und ihr Fundamentalsystem von großer Bedeutung.

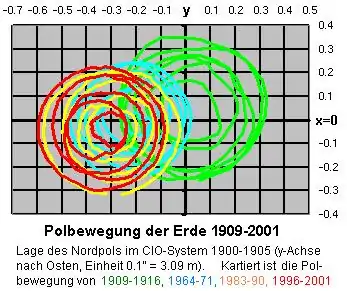
Polbewegung des Nordpols von 1909 bis 2001; die positive x-Achse (nach oben) entspricht der Datumsgrenze, die positive y-Achse (nach rechts) dem 90. Längengrad Ost.

Dass Nord- und Südpol der Erde nicht völlig unveränderlich sind, haben einzelne Astronomen schon vor 150 Jahren vermutet. Inzwischen weiß man, dass sich der Nordpol in einer annähernd jährlichen, spiralförmigen Schwingung von einigen Metern Amplitude über die Erdoberfläche bewegt und außerdem um 10–12 Meter pro Jahrhundert ungefähr in Richtung 80° West driftet. Letzteres wird auch als Polwanderung bezeichnet.

Das periodische leichte Taumeln (umgangssprachlich „Eiern“) der Erdachse hat seine Ursache darin, dass die Drehachse und die Hauptträgheitsachse nicht ganz zusammenfallen und der Erdkörper etwas elastisch ist. Deshalb reagiert der Erdkörper geringfügig auf jahreszeitliche oder tektonische Massenverschiebungen. Die Polbewegung muss für genaue Koordinaten- und Bezugssysteme der Erde und des Weltraums berücksichtigt werden (siehe ICRS und ITRF).

Als Bezugspunkt für den geografischen Nord- und Südpol hat man den von 1900 bis 1905 gemittelten Schnittpunkt der Rotationsachse mit der Erdoberfläche festgelegt und CIO (Conventional International Origin) genannt. Die Polbewegung ist nicht zu verwechseln mit der Veränderung der Ausrichtung der Rotationsachse der Erde im Raum (siehe Himmelspol). Die Gravitationskräfte von Mond, Sonne und den übrigen Planeten üben Drehmomente auf den Erdkörper aus, die zu zyklischen Präzessions- und Kippbewegungen der Erdachse in Zeiträumen von mehreren 10.000 bis 100.000 Jahren führen, die auch Einfluss auf das globale Klima haben (siehe Milanković-Zyklen). Die hier beschriebene Polbewegung ist außerdem nicht zu verwechseln und steht auch nicht in unmittelbarem Zusammenhang mit der Wanderung der magnetischen Pole der Erde.

Grundlegendes

Die Rotationsachse der Erde hat – wie die Drehachse jedes stabilen Kreisels – die Tendenz, ihre Richtung im Raum genau beizubehalten (siehe auch Inertialsystem). Sie weist also während des jährlichen Umlaufs um die Sonne immer in fast dieselbe Richtung – derzeit zum sogenannten Polarstern im Sternbild Kleiner Bär – obwohl ihre Jahresbahn dazu schräg verläuft.

Wäre die Erde völlig starr und keinen Kräften von außen ausgesetzt, würde ihre Drehachse über Jahrmillionen aufgrund der Drehimpulserhaltung in genau dieselbe Richtung weisen. Tatsächlich bewirken jedoch die Anziehungskräfte im Planetensystem (insbesondere die Gravitation von Mond und Sonne) eine kleine, regelmäßige Kippung, weil die Erde etwas von der Kugelgestalt abweicht. Diese sog. Präzession und ein verwandter Effekt, die Nutation, haben zwar nicht direkt mit der Polbewegung zu tun, werden aber oft mit ihr verwechselt.

Die im vorliegenden Artikel behandelte Polbewegung ist die Folge der Tatsache, dass die Erde

kein starrer Körper ist, sondern eine gewisse Elastizität aufweist,
keine Kugel ist, sondern um 0,3 Prozent abgeplattet,
an ihrer Oberfläche jahreszeitliche Effekte und kleine Deformationen auftreten, und
im Erdinnern langsame Massenverschiebungen stattfinden.

Die inneren und äußeren Formveränderungen der Erde (Faktoren 3 und 4) bedeuten, dass sich mit der Massenverteilung auch die Achse des größten Trägheitsmomentes ändert: die Erdachse reagiert mit einem geringfügigen Taumeln, sodass die geografischen Breiten und Längen von Messstationen nicht mehr als unveränderlich gelten können. Der früher klar definierte Zusammenhang zwischen dem erdfesten und dem Himmelskoordinatensystem (verlängerte Erdachse = Himmelspol) wird komplizierter, wenn man die heutigen Ansprüche und hohen Messgenauigkeiten berücksichtigen will.

Historisches

Obwohl die Polbewegung nur wenige Meter ausmacht, wurde der Effekt bereits bis 1844 von Friedrich Wilhelm Bessel beobachtet, um 1860 als Ursache vermutet und 1885 vom Bonner Astronomen Karl Friedrich Küstner durch genaue Messungen der „Polhöhe“ (astronomische Breite) nachgewiesen. Aus längeren Messreihen ließen sich die vermuteten Änderungen der Erdachse als kleine periodische Breitenänderungen von etwa ±0,3″ herausfiltern. Erst gegen Ende des 19. Jahrhunderts hatten die astro-geodätischen Messungen mit Passageninstrumenten und Zenitteleskopen diese Genauigkeitsstufe erreicht.

Perioden und Deutung der Polbewegung

Der von der instantanen Rotationsachse der Erde in den Jahren 2001 bis 2005 am Nordpol zurückgelegte Weg

Die genauesten empirischen Untersuchungen der Polbewegung wurden neben Küstner vom Wiener Geodäten Richard Schumann und dem US-amerikanischen Astronomen Seth Carlo Chandler vorgenommen. Letzterer entdeckte dabei 1891 die Chandler-Periode, die etwa 435 Tage beträgt. Demgegenüber hatte Leonhard Euler für eine starre Erde einen theoretischen Wert von rund 305 Tagen abgeleitet (Euler-Periode). Die theoretische Basis hierfür ist folgende:

Die Symmetrieachse der Erde fällt nicht genau mit ihrer Drehachse zusammen, die durch den Schwerpunkt des Erdkörpers verläuft. Darum „taumelt“ der Erdkörper ein wenig bezüglich seiner eigenen Drehachse, was sich in Änderungen der geografischen Koordinaten eines ortsfesten Beobachters bemerkbar macht. Ein solches Taumeln ist nur stabil, wenn die Drehung (näherungsweise) um die Körperachse mit dem größten oder dem kleinsten Trägheitsmoment stattfindet. Ist das nicht der Fall, nimmt das Taumeln langfristig zu und der Drehkörper orientiert sich so lange um, bis eine der beiden genannten Körperachsen (näherungsweise) mit der Drehachse zusammenfällt. Da die Symmetrieachse der Erde wegen der Erdabplattung die Achse mit dem größten Trägheitsmoment ist, tritt eine solche Instabilität nicht auf. Die Abweichung zwischen Symmetrie- und Drehachse bleibt daher begrenzt und die Symmetrieachse vollführt etwa einmal im Jahr eine präzessionsähnliche Bewegung um die Drehachse.

Das Verhalten des „Erd-Kreisels“ und sein leichtes Taumeln kann mit den Methoden der wissenschaftlichen Mechanik genau berechnet werden, wenn man für ihn einen starren Festkörper mit den Maßen der Erde annimmt. Gibt der Erdkörper (vor allem das plastische Erdinnere) hingegen etwas nach – was die Geologie anhand gefalteter Gesteine schon lange weiß – verlängert sich die Periode dieses Taumelns, weil die Störkräfte nicht mehr so „griffig“ ansetzen können.

Die Gesamtschwingung setzt sich zusammen aus einer freien und einer erzwungenen Komponente. Die freie Schwingung hat eine Amplitude von ca. 6 m und eine Periodendauer von 415 bis 433 Tagen (Chandlersche Periode). Die Schwankung der Periodendauer hängt mit jahreszeitlichen Effekten zusammen (Laubfall und Vegetation, Vereisung, Plattentektonik usw.), die auf Massenverschiebungen an der Erdoberfläche oder im Erdinneren zurückgehen. Aus dem Unterschied zwischen Chandler- und Euler-Periode kann die Starrheit des Erdkörpers berechnet werden, was allerdings durch ihre Schichtung in Erdkruste und Erdmantel erheblich erschwert wird. Doch lässt sich die Verformbarkeit der Erde auch mit anderen Methoden bestimmen, z. B. mittels der Erdgezeiten.

Die erzwungene Schwingung hat eine etwa halb so große Amplitude und eine jährliche Periode. Sie wird durch jahreszeitliche Verlagerungen von Wasser- und Luftmassen angeregt. Die Überlagerung der beiden unterschiedlich lang dauernden Schwingungen führt dazu, dass die Amplitude der Gesamtschwingung in etwa sechsjährigem Rhythmus zwischen ca. 2 m und ca. 8 m schwankt.

Dieser Spiralbewegung überlagern sich kleinere Schwingungen mit Perioden von wenigen Stunden bis zu Jahrzehnten. Auch spontane kleine Verlagerungen sind manchmal festzustellen, die einige Zentimeter betragen – ausgelöst etwa durch das Seebeben vom 26. Dezember 2004 bei Sumatra, das im Indik den gewaltigen Tsunami auslöste.

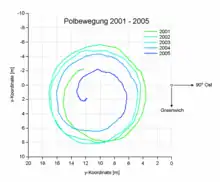
Der Mittelpunkt der Schwingung driftet mit einer Geschwindigkeit von etwa 10 m pro Jahrhundert in Richtung 80° West. Diese Bewegung wird auf großräumige tektonische Vorgänge zurückgeführt.

Internationaler Breitendienst, IPMS und IERS

Um diese Effekte genauer zu untersuchen, wurde 1899 der Internationale Breitendienst gegründet. Er bestand aus fünf Sternwarten auf verschiedenen Kontinenten, die aber alle auf 39,8° nördlicher Breite lagen. Durch allabendliche Messung der astronomischen Breite erhielt man eine kontinuierliche Kurve der Polbewegung, wobei die kleinen (unvermeidlichen) Widersprüche der Daten gegenüberliegender Kontinente durch Ausgleichungsrechnung minimiert wurden.

Einige Jahre nach Beginn der Raumfahrt konnten die astronomischen Messungen durch Methoden der Satellitengeodäsie ergänzt, und bald auch verbessert werden. Dafür wurde der International Polar Motion Service gegründet (Abkürzung IPMS). Er ging in den 1990er Jahren in den Erdrotationsdienst IERS über, dessen Resultate nun auf den Daten von fünf bis sechs sehr unterschiedlichen Messmethoden beruhen.

Siehe Spezialartikel: Fundamentalastronomie.

Theorie

Jahreszeitliche Welle

Abbildung 3. Vektor m der jahreszeitlichen Komponente der Polbewegung als Funktion der Jahreszeit. Die Zahlen und die Strichmarken geben den Beginn eines Kalendermonats an. Die gestrichelte Linie ist die Richtung der großen Ellipsenachse. Die Linie in Richtung der kleinen Achse ist die Lage der Anregungsfunktion als Funktion der Jahreszeit. (100 mas (Milliarcsekunden) = 3,09 m auf der Erdoberfläche).

Es besteht heute allgemeine Übereinstimmung, dass die jahreszeitliche Komponente eine erzwungene Schwingung ist, die im Wesentlichen durch atmosphärische Dynamik zustande kommt.[1] Verantwortlich dafür ist eine stehende antisymmetrische atmosphärische Gezeitenwelle der meridionalen Wellenzahl $m=1$ und der Periode von einem Jahr, die eine Druckamplitude in erster Näherung proportional zu $\sin \theta \cos \theta$ (mit dem Polabstand $\theta$ ) besitzt. Im Winter auf der Nordhemisphäre existiert ein Hochdruckgebiet über dem Nordatlantik und ein Tiefdruckgebiet über Sibirien mit Temperaturdifferenzen bis zu 50°. Im Sommer ist es umgekehrt. Das bedeutet eine Massenimbalance (Unwucht) auf der Erdoberfläche, die eine Kreiselbewegung der Figurenachse des Erdkörpers gegen ihre Rotationsachse zur Folge hat.

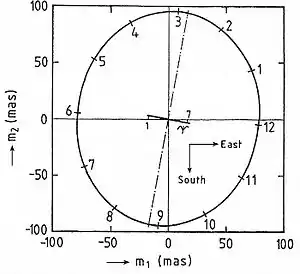
Aus den eulerschen Gleichungen findet man die Position der Polbewegung. Die Position des Vektors m der jahreszeitlichen Komponente der Polbewegung beschreibt eine Ellipse (Abb. 3), deren große und kleine Achse im Verhältnis[2]

{\frac {m_{1}}{m_{2}}}=\nu _{C}\,

(1)

stehen (mit $\nu _{C}=0{,}83$ der Chandler-Resonanzfrequenz; oder einer Chandler-Resonanzperiode von $\tau _{C}=441$ siderischen Tagen = 1,20 siderischen Jahren). Das Ergebnis in Abb. 3 ist in guter Übereinstimmung mit den Beobachtungen.[3][4] Die Druckamplitude der atmosphärischen Welle, die dieses Wobbeln erzeugt, ist $p_{o}=2{,}2\,\mathrm {hPa}$ mit einem Maximum bei $\lambda _{o}$ = −170° geographischer Länge.

Es ist schwierig, den Einfluss des Ozeans zu bestimmen. Seine Wirkung ist zu 5–10 % abgeschätzt worden.[5]

Chandler-Wobbel

Während die Jahreskomponente von Jahr zu Jahr ziemlich konstant bleibt, schwankt die beobachtete Chandler-Periode im Laufe der Jahre erheblich. Diese Schwankung wird durch die empirische Formel[4]

m={\frac {3{,}7}{(\nu -0{,}816)}}

(für

0{,}83<\nu <0{,}9

)

(2)

ziemlich gut beschrieben. Der Betrag m wächst mit der reziproken Frequenz. Eine Erklärung für das Chandler-Wobbeln ist die Anregung durch quasiperiodische atmosphärische Dynamik. In der Tat hat man aus einem gekoppelten Atmosphäre-Ozean-Modell eine Quasi-14-Monatsperiode herausgelesen,[6] und es ist ein regionales 14-Monats-Signal in der Ozean-Oberflächentemperatur beobachtet worden.[7]

Zur theoretischen Behandlung der eulerschen Gleichungen muss die (normierte) Frequenz $\nu$ durch eine komplexe Frequenz $\nu +i\nu _{D}$ ersetzt werden, wobei der imaginäre Term $\nu _{D}$ Dissipationseffekte auf Grund des elastischen Erdkörpers simuliert. Wie in Abb. 3 setzt sich die Lösung aus einer prograden und einer retrograden zirkular polarisierten Welle zusammen. Für Frequenzen $\nu <0{,}9$ kann die retrograde Welle vernachlässigt werden, und es bleibt die zirkular polarisierte prograde Welle, wobei der Vektor m sich auf einem Kreis entgegen dem Uhrzeigersinn bewegt. Der errechnete Betrag von m ist[2]

m=14{,}5\,p_{o}\,{\frac {\nu _{C}}{\sqrt {{((\nu -\nu _{C})}^{2}+\nu _{D}^{2})}}}\,

(für

\nu <0{,}9

)

(3)

Dies ist eine Resonanzkurve, deren Flanken durch

m\approx 14{,}5\,p_{o}\,{\frac {\nu _{C}}{|\nu -\nu _{C}|}}

(für

{(\nu -\nu _{C})}^{2}\gg \nu _{D}^{2}\,\,

)

(4)

approximiert werden können. Die Maximalamplitude von m bei $\nu =\nu _{C}$ wird

m_{\mathrm {max} }=14{,}5\,p_{o}\,{\frac {\nu _{C}}{\nu _{D}}}\,

(7)

Im Bereich der Gültigkeit der empirischen Formel Gl. (2) besteht gute Übereinstimmung mit Gl. (4). Aus den Beobachtungen der letzten 100 Jahre ergibt sich, dass bisher kein größerer Wert als $m_{\mathrm {max} }\sim 230\,$ mas (Milliarcsekunden) gefunden wurde. Das ergibt eine untere Grenze für $\tau _{D}={\frac {1}{\nu _{D}}}\geq 100\,$ Jahre. Die entsprechende Druckamplitude der atmosphärischen Welle ist $p_{o}\sim 0{,}2\,\mathrm {hPa}$ . Diese Zahl ist in der Tat klein und deutet auf den Resonanzeffekt in der Umgebung der Chandlerschen Resonanzfrequenz hin.

Polkoordinaten

Die vom IERS regelmäßig bestimmten Erdrotationsparameter beschreiben neben der momentanen Drehgeschwindigkeit der Erde und der momentanen Ausrichtung der Drehachse im Raum auch die momentane Ausrichtung des Erdkörpers bezüglich der Drehachse.

Die Polkoordinaten $x$ und $y$ geben die Lage der momentanen Drehachse (genauer: des Celestial Ephemeris Pole) bezüglich eines bestimmten fixen Punktes auf der Erdoberfläche (des IERS Referenzpols) an. Die x-Achse verläuft in Richtung des Nullmeridians (genauer: des IERS-Referenzmeridians) und die y-Achse in Richtung 90° West. Als Maßeinheit werden meist Millibogensekunden verwendet (der Abstand beider Punkte auf der Erdoberfläche lässt sich auch in Metern ausdrücken).

Im Zuge der Polbewegung ändert sich auch die Lage eines ortsfesten Beobachters bezüglich der Drehachse. Führt dieser Beobachter eine astronomische Bestimmung seiner geografischen Koordinaten durch, so erhält er je nach momentaner Lage der Drehachse leicht unterschiedliche Ergebnisse. Ist seine mittlere astronomische Länge $\lambda _{m}$ und seine mittlere Breite $\varphi _{m}$ und hat die instantane Drehachse die Polkoordinaten $x$ und $y$ , so betragen die festgestellten Abweichungen von seinen mittleren Koordinaten in erster Näherung

\Delta \varphi =x\cos \lambda _{m}-y\sin \lambda _{m}

\Delta \lambda =(x\sin \lambda _{m}+y\cos \lambda _{m})\tan \varphi _{m}

.

Geophysikalische Implikationen

Denkt man sich die Erde als genaue, starre Kugel und völlig symmetrisch rotierend, würde die Erdachse unveränderlich sein und Nord- und Südpol in derselben Position auf der Kugel verbleiben. Tatsächlich hat die Erde jedoch

eine Abplattung, wodurch die von außen angreifenden Kräfte nicht mehr symmetrisch sind;
eine gewisse Elastizität und daraus folgende Schwingungen (siehe z. B. Erdbeben)
und Plastizität (Verformbarkeit in längeren Zeiträumen), erkennbar z. B. an geologischen Faltungen bei der Gebirgsbildung oder an der Kontinentalverschiebung,
sowie jahreszeitliche Änderungen (Atmosphäre, Meeresströmungen, Vegetation usw.)

Dadurch vollzieht die wahre Erdachse sehr komplizierte, aber großteils periodische Bewegungen. Die Massenverlagerungen auf und in der Erde und die Nachgiebigkeit des Erdkörpers lassen sich durch geeignete physikalische Modelle teilweise theoretisch, teilweise empirisch berechnen und jedes Jahr etwas verfeinern.

Im Jahr 2003 wurde der Descartes-Preis Véronique Dehant vom Observatoire royal de Belgique und einer europaweiten Gruppe von etwa 30 Forschern zuerkannt, die unter ihrer Leitung eine erweiterte Theorie der Erdrotation und der Nutation entwickelten.

Anwendungen und Reduktionen

Die genaue Kenntnis der Lage der Erdachse ist neben der Forschung auch für mehrere Zwecke der Praxis erforderlich. Dazu zählen die Satellitennavigation, die Geoidbestimmung, die Reduktion geodätischer Präzisionsmessungen (siehe Lotabweichung) und auch die Raumfahrt. Würde man die aktuelle Pollage nicht berücksichtigen, wären Fehler in der Position von mehr als 10 Metern die Folge. Beispielsweise würde ein 100 km großes Netz einer Landesvermessung Differenzen von cm bis dm erleiden, oder eine Marsrakete würde ihr Ziel um mehrere 1000 Kilometer verfehlen.

Literatur

J.M. Wahr: The Earth’s Rotation, Ann. Rev. Earth Planet. Sci., 16, 231, 1988
H. Volland: Atmosphere and Earth’s Rotation. Surv. Geophys., 17, 101, 1996
K. Lambeck: The Earth’s Variable Rotation: Geophysical Causes and Consequences. Cambridge University Press, Cambridge 1980
H. Jochmann: The Earth rotation as a cyclic process and as an indicator within the Earth’s interior. Z. geol. Wiss., 12, 197, 1984
J.M. Wahr: The effects of the atmosphere and oceans on the Earth’s wobble – I. Theory. Geophys. Res. J. R. Astr. Soc., 70, 349, 1982
S. Hameed, R.G. Currie: Simulation of the 14-month Chandler wobble in a global climatic model. Geophys. Res. Lett., 16, 247, 1989
I. Kikuchi, I. Naito: Sea surface temperature analysis near the Chandler period. Proceedings of the International Latitude Observatory of Mizusawa, 21 K, 64, 1982

Siehe auch

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] J.M. Wahr: The Earth’s Rotation, Ann. Rev. Earth Planet. Sci., 16, 231, 1988

[VollandAR-2] H. Volland: Atmosphere and Earth’s Rotation. Surv. Geophys., 17, 101, 1996

[3] K. Lambeck: The Earth’s Variable Rotation: Geophysical Causes and Consequences. Cambridge University Press, Cambridge 1980

[Jochmann-4] H. Jochmann: The Earth rotation as a cyclic process and as an indicator within the Earth’s interior. Z. geol. Wiss., 12, 197, 1984

[5] J.M. Wahr: The effects of the atmosphere and oceans on the Earth’s wobble – I. Theory. Geophys. Res. J. R. Astr. Soc., 70, 349, 1982

[6] S. Hameed, R.G. Currie: Simulation of the 14-month Chandler wobble in a global climatic model. Geophys. Res. Lett., 16, 247, 1989

[7] I. Kikuchi, I. Naito: Sea surface temperature analysis near the Chandler period. Proceedings of the International Latitude Observatory of Mizusawa, 21 K, 64, 1982