Sternzeit

Die Sternzeit ist eine in der Astronomie gebrauchte Zeitskala und beruht auf der scheinbaren Bewegung der Sterne als Folge der Eigendrehung der Erde. Ein Sterntag ist die Dauer, die der Sternhimmel (genauer: der Frühlingspunkt) für eine ganze scheinbare Umrundung der Erde benötigt. Im Vergleich zur gewöhnlich benutzten Sonnenzeit, die auf der scheinbaren Umrundung der Erde durch die Sonne beruht, ist der Sterntag knapp vier Minuten kürzer als der Sonnentag.

Der Sterntag wird wie der Sonnentag auch in 24, aber kürzere Stunden eingeteilt.[1] Er beginnt, wenn der Frühlingspunkt den Meridian des Beobachtungsortes passiert und endet dort bei dessen nächster Passage. Der Beobachter – in der Regel ein Astronom in einer Sternwarte – schließt aus der Sternzeit auf den momentanen Himmelsanblick.[2] Die Sternzeit ist aus dem Rektaszensions-Winkel – einer primären Größe für die Stellung der Sterne am Himmel – abgeleitet. Ein Stern mit zum Beispiel 15° Unterschied in Rektaszension zum Frühlingspunkt passiert den Meridian eine Sternstunde später als letzterer. Dieser Sachverhalt lässt sich kurz damit angeben, dass es zum Beispiel 1:00 Uhr Sternzeit ist. Zu beachten ist aber, dass die Sternzeit eine an den Ort gebundene Zeit ist. Zum erleichterten Zeitvergleich für Beobachtungen, die an verschiedenen Orten erfolgen, werden die örtlichen Sternzeituhren auf die Sternzeit von Greenwich eingestellt. Der Zeitunterschied ist – gleich wie bei der Sonnenzeit – 1 Stunde für 15° Längendifferenz zwischen den Beobachtungsorten.

Die Beobachtungsarbeit unter Verwendung der Sternzeit hat den Vorteil, dass zur gleichen Sternzeit die Sterne immer in der gleichen Richtung am Himmel stehen. Gegenüber der gewöhnlichen Uhr geht die Sternzeit-Uhr täglich etwa 4 weitere Minuten vor. Nach einem Jahr überholt sie letztere und stimmt mit ihr kurzzeitig wieder überein.

Die allgemeine Zeitbestimmung nach Universal Time (UT) (eine Sonnenzeit) wird in der Praxis durch die exakter mögliche Beobachtung der Sternstellungen vorgenommen. Die so ermittelte Sternzeit wird über eine per Konvention festgelegte Formel (siehe unten) in die zugehörige UT umgerechnet.

Definition und Eigenschaften

Die Sternzeit ist definiert als der Stundenwinkel des Frühlingspunktes. Bezieht man sich auf den mittleren Frühlingspunkt, so erhält man die mittlere Sternzeit. Bezieht man sich auf den wahren Frühlingspunkt, so erhält man die scheinbare oder wahre Sternzeit.[3]

Die Ursache für das kontinuierliche Anwachsen des genannten Stundenwinkels ist die Erdrotation. Die Sternzeit unterliegt damit allen kurz- und langfristigen Ungleichmäßigkeiten der Erdrotation und ist daher kein gleichförmig verlaufendes Zeitmaß. Sie ist aber stets ein getreues Abbild des Drehwinkels der Erde bezüglich des Frühlingspunktes.

Da der Frühlingspunkt sich wegen der Präzession gegenüber dem Fixsternhintergrund bewegt, ist ein Sterntag (d. h. eine volle Umdrehung der Erde bezüglich des Frühlingspunktes) etwas kürzer als eine Erdrotation (d. h. eine volle Umdrehung der Erde bezüglich des Fixsternhintergrundes). Da der Frühlingspunkt sich pro Tag um etwa 0,137 Bogensekunden rückläufig entlang der Ekliptik bewegt, fällt ein mittlerer Sterntag um 0,009 Sekunden kürzer aus als eine Erdrotation.[4]

Der wahre Frühlingspunkt unterscheidet sich um die ihrerseits veränderliche Nutation vom mittleren Frühlingspunkt. Die scheinbare Sternzeit unterliegt daher gegenüber der (selbst schon ungleichförmigen) mittleren Sternzeit einer zusätzlichen Ungleichförmigkeit, deren Hauptkomponente mit einer Periode von 18,6 Jahren und einer Amplitude von ±1,05 Sekunden schwankt.[5]

Der Stundenwinkel des Frühlingspunktes ist derselbe für Beobachter, die sich auf demselben Längengrad befinden, für Beobachter auf verschiedenen Längengraden jedoch unterschiedlich. Die daraus abgeleitete Sternzeit ist also eine Ortszeit. Die Sternzeit des Referenzortes Greenwich ist die Greenwicher Sternzeit. Sie wird in Berechnungen besonders häufig benötigt. Die verschiedenen Arten von Sternzeit werden oft durch ihre englischen Abkürzungen bezeichnet:

LAST: local apparent sidereal time, scheinbare Ortssternzeit
LMST: local mean sidereal time, mittlere Ortssternzeit
GAST: Greenwich apparent sidereal time, scheinbare Greenwicher Sternzeit
GMST: Greenwich mean sidereal time, mittlere Greenwicher Sternzeit

Der Stundenwinkel des Frühlingspunktes ist der entlang des Himmelsäquators gezählte Winkel vom Meridian zum Frühlingspunkt. Die Rektaszension eines Sterns andererseits ist der entlang des Himmelsäquators gezählte Winkel vom Frühlingspunkt zum Stern. Steht der Stern auf dem Meridian (das heißt: kulminiert der Stern), so sind beide Winkel gleich groß. Daraus folgt: Im Augenblick der Kulmination eines Sternes ist die Sternzeit gleich der Rektaszension des Sternes.

Die Sternzeit ist die Rektaszension in der oberen Kulmination.

Dies lässt sich benutzen, um durch Beobachtung des Kulminationszeitpunktes unmittelbar die Rektaszension des Sterns zu bestimmen. Das ist der Grund, warum die Rektaszension oft in Zeiteinheiten statt in Winkeleinheiten angegeben wird: sie ist dann unmittelbar die zum Zeitpunkt der Kulmination abgelesene Sternzeit. Wega zum Beispiel hat eine Rektaszension von 18^h 36^m 56^s, wird also stets um 18^h 36^m 56^s Ortssternzeit kulminieren.

Andererseits kann durch Beobachtung der Kulmination eines Sterns bekannter Rektaszension die momentane Sternzeit bestimmt werden: Wenn Wega kulminiert, beträgt die Sternzeit 18^h 36^m 56^s (in der Praxis sind noch Korrekturen wegen Präzession, Eigenbewegung, Parallaxe usw. anzubringen).

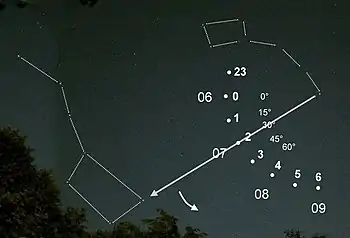
1. Der „Stern-Stundenzeiger“ dreht sich auf einem am Horizont fixen Zifferblatt:
Nach einer 15°-Drehung (Skala 0°, 15°, 30°, …) ist eine Sternzeitstunde (Skala 23, 0, 1, …) vergangen.
2. Der „Stern-Stundenzeiger“ dreht sich auf einem von der Sonne mitgeschleppten, um den Polarstern drehbaren Zifferblatt:
Nach etwa einem Monat (Skala 06, 07, 08, …) ist er der Sonne um 30° (Skala 0°, 15°, 30°, …) vorausgeeilt.

Drehung des Sternhimmels

Tägliche Drehung

Man kann sich den Sternhimmel als große Uhrscheibe vorstellen, die sich an einem Sterntag dem Uhrzeigersinn entgegen (auf der Nordhalbkugel) einmal um sich selbst dreht. Im Bild ist diese Scheibe mit einem Zeiger zwischen Polarstern und Großem Bären markiert. Das 24-Stunden-Zifferblatt (Skala 23, 0, 1, …) ist am Horizont fixiert. Hat sich der Zeiger um 15° weiter gedreht (Skala 0°, 15°, 30°, …), ist eine Sternzeitstunde vergangen. Für eine Sonnenzeitstunde muss er sich geringfügig weiter drehen.

Jährliche Drehung

Auf einem von der Sonne mitgeschleppten, sich um den Polarstern drehenden Zifferblatt stellt man ein sehr langsames Vorrücken des Zeigers fest. Der Zeiger umrundet es einmal im Jahr: 30° (Skala 0°, 15°, 30°, …) in etwa einem Monat (Skala 06, 07, 08, …).

Das Bild wurde Anfang Juli (Ziffer 07) gegen 2:00 Uhr aufgenommen. Zwei Stunden später (etwa 4:00 Uhr) ist der Große Wagen zur Ziffer 4 weiter gewandert. Einen Monat später im August (Ziffer 08) befindet er sich um 2:00 Uhr schon bei der Ziffer 4.

Sterntag und Sonnentag

Sterntag (1 nach 2) und
Sonnentag (1 nach 3),
(Die Schräge der Erdachse auf Erdbahn ist hier vernachlässigt worden.)

Der Sonnentag als Basis der allgemein gebräuchlichen Sonnenzeit dauert geringfügig länger als der Sterntag, weil sich die Sonne geringfügig langsamer als die Sterne – auch scheinbar – um die Erde bewegt. Der Grund dafür ist erneut die eigene Bewegung der Erde, nämlich ihre jährliche Umrundung der Sonne. Innerhalb eines Tages bewegt sich die Erde auf ihrem jährlichen Weg um die Sonne rund ein Grad voran. Somit muss sie sich um so viel nach einer vollen Umdrehung weiter drehen, bis die Sonne wieder in derselben Richtung steht und dafür braucht sie rund vier Minuten.[6]

Der Sterntag ist etwa 1/365 (Länge des Jahres gleich 365,2422 Tage) kürzer als der Sonnentag. An den 24 Stunden des Sonnentags gemessen ist der Sterntag 23 Stunden, 56 Minuten und 4,091 Sekunden lang. Der Sterntag wird selbst wieder in 24 Stunden, seine Stunden in 60 Minuten und seine Minuten in 60 Sekunden unterteilt.

Durch die Nutation der Erde schwankt der Frühlingspunkt mit einer Periode von etwa 18,6 Jahren. Dementsprechend unterscheidet man die wahre Sternzeit, die sich aus der direkten Beobachtung ergibt, und die mittlere Sternzeit, die von diesen Schwankungen befreit ist. Der Unterschied zwischen wahrer und mittlerer Sternzeit beträgt maximal etwa 1,1 Sekunden.

Sternzeit und Sternbeobachtung

Die Kenntnis der Sternzeit erleichtert die Beobachtung von Gestirnen wesentlich. In Sternwarten benutzt man Uhren, die die Sternzeit anzeigen. Sie gehen synchron mit den am Himmel laufenden Sternen. Auf einem festen Standort hat jeder Sterndurchgang durch eine bestimmte Höhe oder Richtung eine fixe Sternzeit und kann daher in einen Beobachtungs-Stundenplan nach Sternzeit unverrückbar eingetragen werden. Zu beachten ist, dass die mögliche nächtliche Beobachtungszeit den Stundenplan einmal im Jahr durchläuft.

Die Sternzeit ist wie die Wahre Sonnenzeit eine lokale Zeit. So wie bei der Wahren Sonnenzeit 12 Uhr (mittags) ist, wenn die Sonne den Orts-Meridian durchläuft, ist bei Sternzeit 0 Uhr, wenn der Frühlingspunkt im Orts-Meridian steht. Die Sternzeit auf eine Zonenzeit zu vereinheitlichen wäre widersinnig. Im Gegenteil: Die in Jahrbüchern für einen Tag enthaltene Sternzeit gilt für einen bestimmten Längengrad. Sie muss auf den Längengrad des Beobachtungsortes umgerechnet werden, um mit ihr nutzbringend arbeiten zu können (+ 4 Minuten Sternzeit pro Grad westlicher).

Aus der Differenz der lokalen Sternzeit eines Orts zur Sternzeit in Greenwich folgt unmittelbar die geografische Länge dieses Orts, siehe astronomische Navigation. Einer Messung dieser lokalen Sternzeit entspricht also entweder eine Ortung oder eine Zeitmessung – je nachdem, ob die Sternzeit in Greenwich zum Beobachtungszeitpunkt oder der Längengrad des Beobachtungsorts bekannt ist.

Sternzeit und Rektaszension

Für die Sternzeit gilt:

Die Sternzeit ist der Stundenwinkel des Frühlingspunkts.
Sternzeit Θ, sowie Stundenwinkel τ und Rektaszension α eines Gestirns sind verknüpft über die Beziehung τ = Θ − α.
Die Sternzeit an einem Ort ist die Rektaszension desjenigen Gestirns, das gerade kulminiert (τ = 0).

Zur Zeit des Herbstäquinoktiums sind Wahre Sonnenzeit und Sternzeit annähernd gleich; denn ein Stern nahe beim Frühlingspunkt kulminiert zu Mitternacht, wenn die moderne 24-Stunden-Zählung beginnt.

Sternzeit und UT

Der Stundenwinkel der Sonne ist die wahre Sonnenzeit. Sie ist unmittelbar beobachtbar und wird von Sonnenuhren angezeigt. Wegen der Neigung der Erdachse und der Elliptizität der Erdbahn verläuft die wahre Sonnenzeit jedoch ungleichförmig (Hauptartikel: Zeitgleichung). Um ein von der Zeitgleichung befreites Zeitmaß zu erhalten, betrachtet man anstelle der wahren Sonne die so genannte fiktive mittlere Sonne, einen gedachten Punkt, welcher mit konstanter Geschwindigkeit entlang des Himmelsäquators (nicht der Ekliptik) läuft. Der Stundenwinkel dieses Punktes ist die nicht der Zeitgleichung unterliegende mittlere Sonnenzeit. Die Lage der fiktiven mittleren Sonne auf dem Himmelsäquator kann nicht durch Beobachtung, sondern nur durch Rechnung bestimmt werden.

Im Jahre 1896 wurde in einer internationalen Übereinkunft der folgende von Simon Newcomb ermittelte Ausdruck für die Rektaszension der fiktiven mittleren Sonne als verbindlich festgelegt:[7]

R_{U}\,=\,18^{\mathrm {h} }\,38^{\mathrm {m} }\,45{,}836^{\mathrm {s} }+8640184{,}542^{\mathrm {s} }\cdot T_{U}+0{,}0929^{\mathrm {s} }\cdot T_{U}^{2}

Dabei ist $\textstyle T_{U}$ die Anzahl der seit dem Greenwicher mittleren Mittag (12^h UT) am 0. Januar 1900 verstrichenen Julianischen Jahrhunderte zu je 36525 mittleren Sonnentagen. Der lineare Term der Gleichung gibt die Geschwindigkeit der fiktiven mittleren Sonne bezüglich des mittleren Frühlingspunkts des Datums an, der quadratische Term berücksichtigt den Umstand, dass die präzessionsbedingte Bewegung des Frühlingspunktes gegenwärtig leicht beschleunigt.

Die Weltzeit UT wurde definiert als der Greenwicher Stundenwinkel der fiktiven mittleren Sonne plus 12 Stunden (die Addition von 12 Stunden ist nötig, weil der Meridiandurchgang der fiktiven mittleren Sonne um 12 Uhr UT stattfinden soll, ihr Stundenwinkel in diesem Augenblick aber 0^h beträgt). Der Stundenwinkel eines Objekts ist aber gleich dem Stundenwinkel des Frühlingspunktes minus der Rektaszension des Objekts, und der Stundenwinkel des Frühlingspunktes wiederum ist per Definition nichts anderes als die Sternzeit. Der Zusammenhang zwischen Weltzeit UT und Greenwicher Sternzeit lautet also:

UT	= 12h + Greenwicher Stundenwinkel der fiktiven mittleren Sonne
	= 12h + Greenwicher Stundenwinkel des Frühlingspunktes – R_U
	= 12h + Greenwicher Sternzeit – R_U

Da die von Newcomb gegebene Rektaszension der fiktiven mittleren Sonne sich auf den mittleren Frühlingspunkt des Datums bezieht, ist die hier auftretende Sternzeit die mittlere Greenwicher Sternzeit.

Jeweils um 12 Uhr UT ist die Greenwicher Sternzeit identisch mit R_U (da dies der Kulminationszeitpunkt der fiktiven mittleren Sonne mit der Rektaszension R_U ist). Daher kann R_U auch als die dem Zeitpunkt 12^h UT entsprechende Greenwicher Sternzeit angesehen werden. Daraus folgt der von 1900 bis 1984 benutzte Ausdruck für die mittlere Greenwicher Sternzeit: zum Zeitpunkt 0^h UT eines jeden Tages ist die zugehörige mittlere Greenwicher Sternzeit[8]

\mathrm {GMST(0^{\mathrm {h} }\,UT)} \,=\,6^{\mathrm {h} }38^{\mathrm {m} }45{,}836^{\mathrm {s} }\,+\,8640184{,}542^{\mathrm {s} }\cdot T_{U}+0{,}0929^{\mathrm {s} }\cdot T_{U}^{2}

Hier wächst T_U, vom Zeitpunkt 1900.0 startend, sukzessive mit der Schrittweite 1/36525. Zu der so für 0h UT bestimmten Sternzeit sind noch die seit 0^h UT verflossenen Sternzeit-Stunden zu addieren (siehe unten).

Mit der Einführung verbesserter astronomischer Konstanten im Jahre 1984 wurde auch diese Formel einer Revision unterzogen. Der Zusammenhang zwischen GMST und UT1 wurde neu definiert als[9][8]

\mathrm {GMST1(0^{\mathrm {h} }\,UT1)} \,=\,24110{,}54841^{\mathrm {s} }\,+\,8640184{,}812866^{\mathrm {s} }\,\cdot \,T_{U}\,+\,0{,}093104^{\mathrm {s} }\,\cdot \,T_{U}^{2}\,-\,{6{,}2\cdot 10^{-6}}^{\mathrm {\,s} }\,\cdot \,T_{U}^{3}

Dabei ist $T_{U}={\tfrac {d_{U}}{36525}}$ und $d_{U}$ die Anzahl der seit dem 1. Januar 2000, 12^h UT1 (JD = 2451545.0 UT1) verstrichenen UT-Tage: d_U = ±0,5, ±1,5, ±2,5, ±3,5, …

Die genannten Gleichungen stellen einen Zusammenhang zwischen der Sternzeit und der Weltzeit UT her. Obwohl UT ihrer Definition gemäß eigentlich vom Sonnenlauf abzuleiten wäre, wurde sie in der Praxis über diese Formeln aus den beobachteten Meridiandurchgängen von Sternen, also der Sternzeit abgeleitet. Sterndurchgänge lassen sich wesentlich präziser beobachten als die Position der überaus hellen und die Instrumente erwärmenden Sonne. Diese Definition von UT1 war bis ins Jahr 2003 gültig. Seither wird UT1 nicht mehr über die Sternzeit, sondern den neu eingeführten „Erdrotationswinkel“ bestimmt.[8]

Bevor die Unregelmäßigkeiten und die langfristige Verlangsamung der Erdrotation erkannt wurden, galten die Sternzeit und die aus ihr abgeleitete UT als strikt gleichmäßige Zeitskalen. Zu Beginn des 20. Jahrhunderts stellten die Astronomen fest, dass die beiden Skalen ungleichförmig verliefen und mussten neue, gleichförmige Zeitskalen einführen. Die von der Erdrotation abgeleiteten Zeitskalen wie UT werden auch als „bürgerliche Zeit“ bezeichnet und weichen zunehmend von gleichmäßigen Zeitskalen wie Ephemeridenzeit, Atomzeit u. ä. ab (Hauptartikel: Delta T).

Berechnung der Sternzeit

Die Formeln können auch benutzt werden, um die Sternzeit aus bekanntem UT zu berechnen.[10]

Sternzeit in Greenwich

Dazu bestimme man zunächst das Julianische Datum JD für den Zeitpunkt 0^h UT am gewünschten Datum (eine auf ,5 endende Zahl). Dann berechne T:

T\,=\,{\frac {JD-2451545{,}0}{36525}}

und damit die mittlere Greenwicher Sternzeit für 0^h UT, je nach Bedarf im Zeit- oder Gradmaß:

{\begin{aligned}\mathrm {GMST(0h\,UT)} \,&=\,6^{\mathrm {h} }41^{\mathrm {m} }50{,}54841^{\mathrm {s} }+8640184{,}812866^{\mathrm {s} }\cdot T+0{,}093104^{\mathrm {s} }\cdot T^{2}-0{,}0000062^{\mathrm {s} }\cdot T^{3}\\&=\,24110{,}54841^{\mathrm {s} }+8640184{,}812866^{\mathrm {s} }\cdot T+0{,}093104^{\mathrm {s} }\cdot T^{2}-0{,}0000062^{\mathrm {s} }\cdot T^{3}\\&=\,100{,}46061837^{\circ }+36000{,}770053608^{\circ }\cdot T+0{,}000387933^{\circ }\cdot T^{2}-(T^{3}/38710000)^{\circ }\end{aligned}}

Zur Bestimmung der Sternzeit GMST für einen beliebigen Zeitpunkt UT des gegebenen Datums multipliziere man UT mit 1,00273790935 (= Synodische Tageslänge / Siderische Tageslänge) und addiere das Ergebnis zur vorhin berechneten Sternzeit für 0^h UT.

Sternzeit am Standort des Beobachters

Ein Beobachter auf der geographischen Länge λ muss noch auf seine Ortssternzeit umrechnen:

{\begin{alignedat}{2}\mathrm {LMST} \,&\,=\mathrm {GMST} +\lambda /15&\quad &{\text{falls GMST im Zeitmaß}}\\&\,=\mathrm {GMST} +\lambda &&{\text{falls GMST im Gradmaß}}\\\end{alignedat}}

Der Winkel LMST ist gegebenenfalls noch auf den Hauptwert (0°–360°) zu bringen, und in das Zeitmaß umzurechnen.

Siehe auch

Siderischer Tag

Weblinks

Online Sternzeitrechner

Einzelnachweise

Eine Sternstunde ist etwa 0,9973 Sonnenstunden lang.
Da sich die Sonne einmal im Jahr durch den Himmel bewegt, ist dieser “momentane Himmelsanblick” während etwa eines halben Jahres nur ein “fiktiver Himmelsanblick”. Die in ihm enthaltenen Himmelskörper können trotz unveränderlicher Sternzeit nämlich bei Tageslicht nicht beobachtet werden.
A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0, S. 312.
H.U. Keller: Astrowissen. Kosmos Verlag, Stuttgart 2000, ISBN 3-440-08074-9, S. 44.
A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0, S. 316.
Hermann-Michael Hahn: Sternzeit um Mitternacht - Wenn die Sternzeituhr richtig geht. In: deutschlandfunk.de. Abgerufen am 6. Januar 2021.
D.D. McCarthy, P.K. Seidelmann: Time – From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4, S. 13.
D.D. McCarthy, P.K. Seidelmann: Time – From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4, S. 15.
S. Aoki, H. Kinoshita, B. Guinot, G.H. Kaplan, D.D. McCarthy, P.K. Seidelmann: The New Definition of Universal Time. Astronomy and Astrophysics, Bd. 105 (1982), Nr. 2, S. 359–361 (bibcode:1982A&A...105..359A).
J. Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Kap. 12.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Eine Sternstunde ist etwa 0,9973 Sonnenstunden lang.

[2] Da sich die Sonne einmal im Jahr durch den Himmel bewegt, ist dieser “momentane Himmelsanblick” während etwa eines halben Jahres nur ein “fiktiver Himmelsanblick”. Die in ihm enthaltenen Himmelskörper können trotz unveränderlicher Sternzeit nämlich bei Tageslicht nicht beobachtet werden.

[3] A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0, S. 312.

[4] H.U. Keller: Astrowissen. Kosmos Verlag, Stuttgart 2000, ISBN 3-440-08074-9, S. 44.

[5] A. Schödlbauer: Geodätische Astronomie. Walter de Gruyter, Berlin / New York 2000, ISBN 3-11-015148-0, S. 316.

[6] Hermann-Michael Hahn: Sternzeit um Mitternacht - Wenn die Sternzeituhr richtig geht. In: deutschlandfunk.de. Abgerufen am 6. Januar 2021.

[7] D.D. McCarthy, P.K. Seidelmann: Time – From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4, S. 13.

[McCarthySeidelmannS15-8] D.D. McCarthy, P.K. Seidelmann: Time – From Earth Rotation to Atomic Physics. Wiley-VCH Verlag, Weinheim 2009, ISBN 978-3-527-40780-4, S. 15.

[9] S. Aoki, H. Kinoshita, B. Guinot, G.H. Kaplan, D.D. McCarthy, P.K. Seidelmann: The New Definition of Universal Time. Astronomy and Astrophysics, Bd. 105 (1982), Nr. 2, S. 359–361 (bibcode:1982A&A...105..359A).

[10] J. Meeus: Astronomical Algorithms. Willmann-Bell, Richmond 2000, ISBN 0-943396-61-1, Kap. 12.