Eispunkt

Der Eispunkt (auch Gefrierpunkt[1] des Wassers oder Schmelzpunkt[1] des Wassers) ist die Temperatur, bei der luftgesättigtes aber sonst reines flüssiges Wasser unter einem Druck von einer Atmosphäre (1013,25 hPa) sowohl mit seinem Eis als auch mit seinem Dampf im Gleichgewicht steht. Diese Temperatur beträgt ungefähr 273,15 K auf der Kelvin-Skala und ungefähr 0 °C auf der Celsius-Skala.

Luftgesättigtes aber sonst reines flüssiges Wasser gefriert, wenn seine Temperatur bei einem Druck von 1013,25 hPa den Eispunkt unterschreitet (und keine Unterkühlung das Gefrieren verzögert). Luftgesättigtes aber sonst reines Wassereis schmilzt, wenn seine Temperatur bei diesem Druck den Eispunkt überschreitet.

Bevor die Definition der Celsius-Skala 1954 an die Definition der Kelvin-Skala angeschlossen wurde, dienten der Eispunkt (definitionsgemäß 0 °C) und der Siedepunkt (definitionsgemäß 100 °C) des Wassers als ihre definierenden Fixpunkte.

Der Sprachgebrauch ist uneinheitlich: Als „Eispunkt“ wird teilweise der betreffende Punkt im Phasendiagramm des Wassers bezeichnet (also das Zahlenpaar 273,15 K und 1013,25 hPa), teilweise die betreffende Temperatur (gewissermaßen als „Punkt“ auf der Temperaturskala). Dasselbe gilt für den Tripelpunkt.

Erläuterung

Übergang vom Tripelpunkt zum Eispunkt

Die Tripelpunktstemperatur des Wassers ist jene Temperatur, bei der reines Wasser und reines Eis mit ihrem Dampf unter der Bedingung im Gleichgewicht stehen, dass der Druck in allen drei Phasen gleich dem Sättigungsdampfdruck des Wassers bei dieser Temperatur ist. Es gibt im Druck-Temperatur-Diagramm des reinen Wassers genau einen Punkt, bei dem dieses Gleichgewicht möglich ist, nämlich bei ungefähr 273,16 K und 611 Pa. Setzt man jedoch einen anderen Druck voraus als den eigenen Sättigungsdampfdruck des Wassers, dann stehen die drei Phasen bei einer anderen Temperatur im Gleichgewicht. Ein anderer Druck kann dadurch erzeugt werden, dass der Gasphase des Systems ein zusätzliches, inertes Gas hinzugefügt wird.

Handelt es sich bei diesem hinzugefügten Gas insbesondere um Luft und wird der Druck so eingestellt, dass der Gesamtdruck von Luft und Wasserdampf 1013,25 hPa beträgt, dann stehen flüssiges Wasser, Wassereis und Wasserdampf bei einer Temperatur im Gleichgewicht, die um etwa 0,01 Grad niedriger ist als die Tripelpunktstemperatur.[2] Diese Verschiebung der Gleichgewichtstemperatur hat zwei Ursachen.

Einfluss des erhöhten Druckes

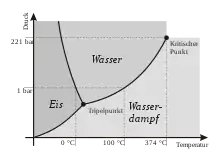
Schematisches Phasendiagramm von Wasser.

Weil die Schmelzkurve im Phasendiagramm des Wassers nach links geneigt ist, verursacht die Erhöhung des Druckes eine Gefrierpunktserniedrigung um etwa 0,0075 Grad: Wird vom Tripelpunkt ausgehend der Druck bei zunächst konstant gehaltener Temperatur erhöht, verlässt das System den Tripelpunkt und gerät in das Gebiet flüssigen Wassers. Hier ist die Eisphase nicht stabil und schmilzt. Ist ein Druck von einer Atmosphäre erreicht, muss die Temperatur um 0,0075 Grad gesenkt werden, damit das System wieder auf die Schmelzkurve gelangt und die Koexistenz von flüssigem Wasser und Eis erneut möglich ist.

Einfluss der gelösten Luft

Weil ein Teil der druckerzeugenden Luft im Wasser in Lösung geht, ist dieses nun kein Reinstoff mehr, sondern eine Mischung. Die Gefrierpunktserniedrigung in Mischungen führt dazu, dass die Temperatur um weitere 0,0025 Grad gesenkt werden muss, um wieder Phasengleichgewicht zu erreichen.

Der Eispunkt ist weniger fundamental als der Tripelpunkt, weil er eine Eigenschaft des Mehrstoffsystems „luftgesättigtes Wasser“ ist, während der Tripelpunkt eine Eigenschaft des Reinstoffsystems „Wasser“ ist.[3]

Eispunkttemperatur

Vereinfacht abgeschätzte Werte für die beiden genannten Beiträge zur Gefrierpunktserniedrigung sind leicht zu erhalten.

Einfluss des erhöhten Druckes

Die Clausius-Clapeyron-Gleichung

{\frac {\mathrm {d} p}{\mathrm {d} T}}\,=\,{\frac {\Delta h}{T\,\Delta v}}

beschreibt die Steigung einer Phasengrenzlinie im p-T-Diagramm. Um die Steigung der Schmelzkurve des Wassers am Tripelpunkt zu ermitteln, sind die Schmelzenthalpie von Eis $\Delta h$ und die Änderung des spezifischen Volumens $\Delta v$ beim Schmelzen einzusetzen:[4]

\textstyle \Delta h=333{,}43\,\mathrm {\frac {kJ}{kg}}

\textstyle \Delta v=-0{,}000091\,\mathrm {\frac {m^{3}}{kg}}

\textstyle T=273{,}16\,\mathrm {K} .

Aufgelöst nach $\mathrm {d} T$ ergibt sich für die Druckänderung $\textstyle \mathrm {d} p=101325\,\mathrm {Pa} -611\,\mathrm {Pa} =100714\,\mathrm {Pa}$ die Gefrierpunktsänderung

\mathrm {d} T_{p}=-0{,}0075\,\mathrm {K}

unter der Annahme, dass die Steigung sich im gesamten überstrichenen Druckbereich nicht merklich ändert.

Einfluss der gelösten Luft

Die Gefrierpunktserniedrigung aufgrund der gelösten Gase ist eine kolligative Eigenschaft, hängt also nicht von der Art der gelösten Teilchen ab, sondern nur von ihrer Anzahl und der Art des Lösungsmittels. Für Wasser als Lösungsmittel beträgt die kryoskopische Konstante $\textstyle 1{,}86\,\mathrm {\frac {K}{mol/kg}}$ . Bei Atmosphärendruck und 0 °C lösen sich aus der Luft 0,00046 Mol Sauerstoff und 0,00081 Mol Stickstoff in einem Kilogramm Wasser.[5] Die molale Konzentration 0,00127 mol/kg der gelösten Atmosphärengase verursacht eine Gefrierpunktserniedrigung von

\mathrm {d} T_{l}=-1{,}86\,\mathrm {\frac {K}{mol/kg}} \cdot 0{,}00127\,\mathrm {\frac {mol}{kg}} =-0{,}0024\,\mathrm {K}

.

Eispunkttemperatur

Eine genaue Rechnung, die auch andere Atmosphärengase, die Temperaturabhängigkeit der Löslichkeiten, die Nicht-Idealitäten der gelösten Stoffe sowie die Druck- und Temperaturabhängigkeiten der thermophysikalischen Eigenschaften des Wassers berücksichtigt, liefert das Ergebnis[6][Anm. 1][Anm. 2]

T_{\mathrm {Eis} }\,=\,(273{,}150019\pm 0,000005)\,\mathrm {K}

.

Dieser Zahlenwert wird üblicherweise auf 273,15 K gerundet.

Gefrierpunkt bei anderen Drücken

Die Rechnung lässt sich auch für andere Drücke führen, die folgende Tabelle listet einige Beispiele auf.[6] Sie ist zum Vergleich um den Tripelpunkt ergänzt:

Druck hPa	Gefrierpunkt reinen Wassers K	Lösungs- effekt mK	Gefrierpunkt luftgesättigten Wassers K
1050	273,152246	−2,591	273,149655
1013,25	273,152519	−2,500	273,150019
1000	273,152618	−2,468	273,150150
0900	273,153360	−2,220	273,151140
0800	273,154103	−1,973	273,152131
0600	273,155589	−1,477	273,154112
0400	273,157075	−0,981	273,156093
0006,11	273,16	00-	000 -

Siehe auch

Der Eispunkt ist nicht zu verwechseln mit dem zur Taupunkttemperatur analogen Reifpunkt oder Frostpunkt, bei dessen Unterschreitung sich Reif absetzt.

Anmerkungen

Aus der Rechnung ergeben sich für die gelösten Gase bei der Eispunkttemperatur die folgenden Stoffmengenanteile in der Lösung: 14,95×10^-6 für N₂, 8,22×10^-6 für O₂, 0,40×10^-6 für Ar, 0,54×10^-6 für molekulares gelöstes CO₂, 0,05×10^-6 jeweils für HCO₃^-- und H⁺-Ionen, in der Summe 24,21×10^-6 für alle gelösten Gase.
Die angegebene Unsicherheit ist die aus den Eingangsdaten und der Rechenmethode folgende Unsicherheit des Temperaturabstands zwischen Tripelpunkt und Eispunkt. Zum Zeitpunkt dieser Untersuchungen hatte die Tripelpunktstemperatur als definierender Fixpunkt einen exakt gegebenen Zahlenwert, die genannte Unsicherheit war also gleichzeitig die Unsicherheit für die absolute Lage der Eispunkttemperatur auf der Kelvin-Skala. Seit der Neudefinition des Kelvin (2019) ist die Tripelpunktstemperatur kein definierender Fixpunkt mehr, sie muss nun gemessen werden und besitzt daher selbst eine gewisse Unsicherheit. Bei Einführung der Neudefinition betrug diese Unsicherheit 0,1 mK (siehe → Tripelpunkt). Die Unsicherheit im Abstand zwischen Tripelpunkt und Eispunkt ist nach wie vor dieselbe, aber die Unsicherheit in der absoluten Lage des Eispunkts ist nun um die Unsicherheit der Lage des Tripelpunkts größer.

Einzelnachweise

Eintrag zu Schmelzpunkt. In: Römpp Online. Georg Thieme Verlag, abgerufen am 23. Mai 2019.
C.F. Bohren, B.A. Albrecht: Atmospheric Thermodynamics. Oxford University Press, New York, Oxford 1998, ISBN 978-0-19-509904-1, S. 222.
U. Grigull: Technische Thermodynamik. 3. Aufl., de Gruyter, Berlin / New York 1977, ISBN 3-11-006405-7, S. 118
M.S. Owen (ed.): 2013 ASHRAE Handbook Fundamentals - SI edition. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. (ASHRAE), ISBN 978-1-936504-46-6, Table 3.
A. F. Holleman, N. Wiberg: Anorganische Chemie. 103. Auflage. 1. Band: Grundlagen und Hauptgruppenelemente. Walter de Gruyter, Berlin / Boston 2016, ISBN 978-3-11-049585-0, S. 741 (Leseprobe: Teil A – Grundlagen der Chemie Der Wasserstoff. Google-Buchsuche).
„1 l Wasser von 0 °C löst – unabhängig vom Gasdruck [...] – 23.2 cm³ Stickstoff bzw. 49.1 cm³ Sauerstoff.“
A.H. Harvey, M.O. McLinden, W.L. Tew: Thermodynamic Analysis and Experimental Study of the Effect of Atmospheric Pressure on the Ice Point. AIP Conference Proceedings, vol. 1552, issue 1, 221–226 (2013), doi:10.1063/1.4819543

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[gelöst-7] Aus der Rechnung ergeben sich für die gelösten Gase bei der Eispunkttemperatur die folgenden Stoffmengenanteile in der Lösung: 14,95×10^-6 für N₂, 8,22×10^-6 für O₂, 0,40×10^-6 für Ar, 0,54×10^-6 für molekulares gelöstes CO₂, 0,05×10^-6 jeweils für HCO₃^-- und H⁺-Ionen, in der Summe 24,21×10^-6 für alle gelösten Gase.

[Unsicherheit-8] Die angegebene Unsicherheit ist die aus den Eingangsdaten und der Rechenmethode folgende Unsicherheit des Temperaturabstands zwischen Tripelpunkt und Eispunkt. Zum Zeitpunkt dieser Untersuchungen hatte die Tripelpunktstemperatur als definierender Fixpunkt einen exakt gegebenen Zahlenwert, die genannte Unsicherheit war also gleichzeitig die Unsicherheit für die absolute Lage der Eispunkttemperatur auf der Kelvin-Skala. Seit der Neudefinition des Kelvin (2019) ist die Tripelpunktstemperatur kein definierender Fixpunkt mehr, sie muss nun gemessen werden und besitzt daher selbst eine gewisse Unsicherheit. Bei Einführung der Neudefinition betrug diese Unsicherheit 0,1 mK (siehe → Tripelpunkt). Die Unsicherheit im Abstand zwischen Tripelpunkt und Eispunkt ist nach wie vor dieselbe, aber die Unsicherheit in der absoluten Lage des Eispunkts ist nun um die Unsicherheit der Lage des Tripelpunkts größer.

[Römpp-1] Eintrag zu Schmelzpunkt. In: Römpp Online. Georg Thieme Verlag, abgerufen am 23. Mai 2019.

[Bohren_222f-2] C.F. Bohren, B.A. Albrecht: Atmospheric Thermodynamics. Oxford University Press, New York, Oxford 1998, ISBN 978-0-19-509904-1, S. 222.

[Grigull_118-3] U. Grigull: Technische Thermodynamik. 3. Aufl., de Gruyter, Berlin / New York 1977, ISBN 3-11-006405-7, S. 118

[ASHRAE2013-4] M.S. Owen (ed.): 2013 ASHRAE Handbook Fundamentals - SI edition. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. (ASHRAE), ISBN 978-1-936504-46-6, Table 3.

[HoWi_741-5] A. F. Holleman, N. Wiberg: Anorganische Chemie. 103. Auflage. 1. Band: Grundlagen und Hauptgruppenelemente. Walter de Gruyter, Berlin / Boston 2016, ISBN 978-3-11-049585-0, S. 741 (Leseprobe: Teil A – Grundlagen der Chemie Der Wasserstoff. Google-Buchsuche).
„1 l Wasser von 0 °C löst – unabhängig vom Gasdruck [...] – 23.2 cm³ Stickstoff bzw. 49.1 cm³ Sauerstoff.“

[Harvey-6] A.H. Harvey, M.O. McLinden, W.L. Tew: Thermodynamic Analysis and Experimental Study of the Effect of Atmospheric Pressure on the Ice Point. AIP Conference Proceedings, vol. 1552, issue 1, 221–226 (2013), doi:10.1063/1.4819543