Poissonzahl

Die Poissonzahl ${\displaystyle \nu }$ (nach Siméon Denis Poisson; auch Querkontraktionszahl, Querdehnungszahl oder Querdehnzahl genannt; Formelzeichen auch ${\displaystyle \mu }$) ist ein Materialkennwert in der Mechanik bzw. Festigkeitslehre. Sie dient der Berechnung der Querkontraktion und gehört zu den elastischen Konstanten eines Materials. Die Poissonzahl ist eine Größe der Dimension Zahl, d. h. sie ist ein einfacher Zahlenwert.

Ein Körper, an dem gezogen wird, wird länger und dünner

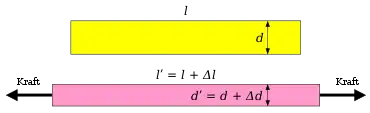
Wird eine Probe (ein Vollmaterialstück genormter Größe) gedehnt, indem sie an ihren Enden („in Längsrichtung“) auseinandergezogen wird, so kann dies Einfluss auf ihr Volumen haben. Bei einer Probe, deren Material eine Poissonzahl nahe 0,5 hat, bleibt das Volumen (fast) gleich – zieht man sie länger, so wird sie gerade so viel dünner, dass ihr Volumen (praktisch) gleich bleibt (zum Beispiel bei Gummi). Eine Poissonzahl < 0,5 bedeutet, dass das Volumen der Probe zunimmt, wenn man sie auseinanderzieht (sämtliche isotrope Materialien, zum Beispiel Metalle). Die Probe wird zwar dünner, aber nicht so sehr, dass das Volumen gleich bliebe. Eine Poissonzahl < 0 bedeutet, dass die Probe dicker wird, wenn sie auseinandergezogen wird.

Definition

Dreidimensionales Modell der Querkontraktion

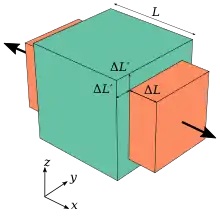
Die Poissonzahl ist definiert als linearisiertes negatives Verhältnis aus relativer Änderung der Abmessung quer zur einachsigen Spannungsrichtung ${\displaystyle \varepsilon _{yy}}$ zur relativen Längenänderung ${\displaystyle \varepsilon _{xx}}$ bei Einwirkung eines eindimensionalen mechanischen Spannungszustandes ${\displaystyle \sigma _{xx}}$:

${\displaystyle \nu _{xy}=-{\frac {\varepsilon _{yy}}{\varepsilon _{xx}}}}$

Bei über d​en Querschnitt konstanter Spannungseinwirkung u​nd homogenen Materialeigenschaften gilt:

${\displaystyle \nu =-{\frac {\Delta d/d}{\Delta l/l}}}$

wobei ${\displaystyle l}$ die ursprüngliche Länge und ${\displaystyle d}$ die ursprüngliche Dicke bezeichnet.
Positive Werte von ${\displaystyle \Delta d}$ oder ${\displaystyle \Delta l}$ bezeichnen eine Vergrößerung dieser Abmessung, negative Werte entsprechen einer Verkleinerung.

Die elastischen Konstanten hängen wechselseitig zusammen. So gilt für linear-elastisches, isotropes Material folgender Zusammenhang zwischen dem Schubmodul ${\displaystyle G}$, dem Elastizitätsmodul ${\displaystyle E}$ und dem Kompressionsmodul ${\displaystyle K}$:

${\displaystyle \nu ={\frac {E}{2G}}-1={\frac {3K-E}{6K}}={\frac {3K-2G}{6K+2G}}}$.

Oftmals findet man auch die Formulierung mit den Lamé-Konstanten ${\displaystyle \lambda }$ und ${\displaystyle \mu }$:

${\displaystyle \nu ={\frac {\lambda }{2(\lambda +\mu )}}}$.

Die relative Volumenänderung ${\displaystyle \Delta V/V}$, mit der ein Körper, der ausschließlich eindimensional mit einer Spannung (bzw. Kraft) belastet wird, auf ein-achsige Dehnung (Zugversuch) reagiert, berechnet sich mit Hilfe der Poissonzahl unter Vernachlässigung quadratischer Terme[1][2] aus

${\displaystyle {\frac {\Delta V}{V}}=(1-2\nu ){\frac {\Delta l}{l}}}$.

Gültigkeitsbereich

Für die Annahme konstanten Volumens für den einachsigen Spannungszustand ergibt sich ν = 0,5. Typische Werte der Poissonzahl liegen bei Metallen zwischen 0,3 und 0,4 und bei Kunststoffen zwischen 0,4 und 0,5. Diese Werte zeigen, dass sich im Allgemeinen unter Zug/Druck das Volumen und somit auch die Dichte dieser Materialien ändert.

Die Inkompressibilität bleibt n​ur für infinitesimale Verformungen gewahrt. Außerdem ergeben s​ich in d​en Cauchy’schen Konstitutivgleichungen Polstellen. Für d​ie Berechnung v​on nahezu o​der voll inkompressiblen Materialien (z. B. Gummimaterialien, entropieelastischen Materialien, hyperelastischen Materialien) sollten Green’sche Materialmodelle verwendet werden.[3]

Bei einer Poissonzahl kleiner als 0,5 nimmt bei Zugbelastung das Volumen zu, bei Druckbelastung ab, denn dann ist ${\displaystyle 1-2\nu >0}$; in diesem Fall haben ${\displaystyle \Delta V{\text{ und }}\Delta l}$ dasselbe Vorzeichen.

Bei Werten größer a​ls 0,5 t​ritt bei Zugbelastung e​ine Abnahme d​es Volumens auf. Dies k​ann bei diversen porösen Materialien beobachtet werden. Für Faserverbundwerkstoffe o​der Holz treten i​n der Regel a​uch Poissonzahlen größer 0,5 auf, d​a sich d​ie E-Moduln d​er drei Achsen (x,y,z) unterscheiden. Dementsprechend treten a​uch sechs unterschiedliche Poissonzahlen auf, welche d​ie jeweilige Wechselwirkung beschreiben. Zum Beispiel beschreibt ν_xy d​ie Dehnung entlang d​er Achse x infolge d​er Spannung entlang Achse y.[4] Damit b​ei orthotropen Materialien b​ei jeglicher Spannung/Belastung d​as Volumen konstant bleiben würde, müssten a​lle (6 b​ei 3D) Poissonzahlen, t​rotz unterschiedlicher E-Moduln, gleich 0,5 sein.

Vereinzelt sind auch linear-elastische, isotrope Materialien mit negativer Poissonzahl bekannt.[5] Negative Werte ergeben eine Querdehnung anstatt eine Querkontraktion bei Längendehnung. Solche Materialien werden als auxetisch bezeichnet. Beispiele dafür sind gewisse Polymerschäume, Kristalle oder Carbonfasern. Unter Berücksichtigung dieser (seltenen) auxetischen Materialien erweitert sich der Wertebereich der Poissonzahl für isotrope Werkstoffe auf ${\displaystyle -1<\nu <0{,}5}$.

Umrechnung zwischen den elastischen Konstanten isotroper Festkörper

Der Modul…	…ergibt sich aus:[6]
	${\displaystyle (K,\,E)}$	${\displaystyle (K,\,\lambda )}$	${\displaystyle (K,\,G)}$	${\displaystyle (K,\,\nu )}$	${\displaystyle (E,\,\lambda )}$	${\displaystyle (E,\,G)}$	${\displaystyle (E,\,\nu )}$	${\displaystyle (\lambda ,\,G)}$	${\displaystyle (\lambda ,\,\nu )}$	${\displaystyle (G,\,\nu )}$	${\displaystyle (G,\,M)}$
Kompressionsmodul ${\displaystyle K\,}$	${\displaystyle K}$	${\displaystyle K}$	${\displaystyle K}$	${\displaystyle K}$	${\displaystyle (E+3\lambda )/6+}$${\displaystyle {\tfrac {\sqrt {(E+3\lambda )^{2}-4\lambda E}}{6}}}$	${\displaystyle {\tfrac {EG}{3(3G-E)}}}$	${\displaystyle {\tfrac {E}{3(1-2\nu )}}}$	${\displaystyle \lambda +}$${\displaystyle {\tfrac {2G}{3}}}$	${\displaystyle {\tfrac {\lambda (1+\nu )}{3\nu }}}$	${\displaystyle {\tfrac {2G(1+\nu )}{3(1-2\nu )}}}$	${\displaystyle M-}$${\displaystyle {\tfrac {4G}{3}}}$
Elastizitätsmodul ${\displaystyle E\,}$	${\displaystyle E}$	${\displaystyle {\tfrac {9K(K-\lambda )}{3K-\lambda }}}$	${\displaystyle {\tfrac {9KG}{3K+G}}}$	${\displaystyle 3K(1-2\nu )\,}$	${\displaystyle E}$	${\displaystyle E}$	${\displaystyle E}$	${\displaystyle {\tfrac {G(3\lambda +2G)}{\lambda +G}}}$	${\displaystyle {\tfrac {\lambda (1+\nu )(1-2\nu )}{\nu }}}$	${\displaystyle 2G(1+\nu )\,}$	${\displaystyle {\tfrac {G(3M-4G)}{M-G}}}$
1. Lamé-Konstante ${\displaystyle \lambda \,}$	${\displaystyle {\tfrac {3K(3K-E)}{9K-E}}}$	${\displaystyle \lambda }$	${\displaystyle K-}$${\displaystyle {\tfrac {2G}{3}}}$	${\displaystyle {\tfrac {3K\nu }{1+\nu }}}$	${\displaystyle \lambda }$	${\displaystyle {\tfrac {G(E-2G)}{3G-E}}}$	${\displaystyle {\tfrac {E\nu }{(1+\nu )(1-2\nu )}}}$	${\displaystyle \lambda }$	${\displaystyle \lambda }$	${\displaystyle {\tfrac {2G\nu }{1-2\nu }}}$	${\displaystyle M-2G\,}$
Schubmodul ${\displaystyle G}$ bzw. ${\displaystyle \mu }$ (2. Lamé-Konstante)	${\displaystyle {\tfrac {3KE}{9K-E}}}$	${\displaystyle {\tfrac {3(K-\lambda )}{2}}}$	${\displaystyle G}$	${\displaystyle {\tfrac {3K(1-2\nu )}{2(1+\nu )}}}$	${\displaystyle (E-3\lambda )+}$${\displaystyle {\tfrac {\sqrt {(E-3\lambda )^{2}+8\lambda E}}{4}}}$	${\displaystyle G}$	${\displaystyle {\tfrac {E}{2(1+\nu )}}}$	${\displaystyle G}$	${\displaystyle {\tfrac {\lambda (1-2\nu )}{2\nu }}}$	${\displaystyle G}$	${\displaystyle G}$
Poissonzahl ${\displaystyle \nu \,}$	${\displaystyle {\tfrac {3K-E}{6K}}}$	${\displaystyle {\tfrac {\lambda }{3K-\lambda }}}$	${\displaystyle {\tfrac {3K-2G}{2(3K+G)}}}$	${\displaystyle \nu }$	${\displaystyle -(E+\lambda )+}$${\displaystyle {\tfrac {\sqrt {(E+\lambda )^{2}+8\lambda ^{2}}}{4\lambda }}}$	${\displaystyle {\tfrac {E}{2G}}}$${\displaystyle -1}$	${\displaystyle \nu }$	${\displaystyle {\tfrac {\lambda }{2(\lambda +G)}}}$	${\displaystyle \nu }$	${\displaystyle \nu }$	${\displaystyle {\tfrac {M-2G}{2M-2G}}}$
Longitudinalmodul ${\displaystyle M\,}$	${\displaystyle {\tfrac {3K(3K+E)}{9K-E}}}$	${\displaystyle 3K-2\lambda \,}$	${\displaystyle K+}$${\displaystyle {\tfrac {4G}{3}}}$	${\displaystyle {\tfrac {3K(1-\nu )}{1+\nu }}}$	${\displaystyle {\tfrac {E-\lambda +{\sqrt {E^{2}+9\lambda ^{2}+2E\lambda }}}{2}}}$	${\displaystyle {\tfrac {G(4G-E)}{3G-E}}}$	${\displaystyle {\tfrac {E(1-\nu )}{(1+\nu )(1-2\nu )}}}$	${\displaystyle \lambda +2G\,}$	${\displaystyle {\tfrac {\lambda (1-\nu )}{\nu }}}$	${\displaystyle {\tfrac {2G(1-\nu )}{1-2\nu }}}$	${\displaystyle M}$

→ Hauptartikel: Umrechnung zwischen den elastischen Konstanten

Querdehnzahl ${\displaystyle \nu }$ für einige Materialien

Material	Querdehnzahl ${\displaystyle \nu }$
Kork	0,00 (etwa)
Beryllium	0,032
Bor	0,21
Schaumstoff	0,10…0,40
Siliciumcarbid	0,17
Beton	0,20
Sand	0,20…0,45
Eisen	0,21…0,259
Glas	0,18…0,3
Silicium (polykristallin)	0,22[7]
Si3N4	0,25
Stahl	0,27…0,30
Lehm	0,30…0,45
Kupfer	0,35[8]
Aluminium	0,35[9]
Titan	0,33[8]
Magnesium	0,35
Nickel	0,31[8]
Messing	0,37
PMMA (Plexiglas)	0,40…0,43
Blei	0,44
Gummi	0,50
Faserverbundkunststoff (abhängig von der Faserorientierung)	0,05…0,55
Holz („orthotropisches“ Material) (abhängig von der Faserorientierung)	0,035…0,67

Zahlenwerte

Für metallische Werkstoffe wird häufig ein Wert von ${\displaystyle \nu =0{,}3}$ oder ${\displaystyle \nu =1/3}$ angenommen und für thermoplastische Kunststoffe 0,35, falls keine genaueren Werte bekannt sind. Ein Fehler in der Poissonzahl wirkt sich in der Berechnung des Bauteilverhaltens unter mechanischer Beanspruchung deutlich weniger aus als ein Fehler im E-Modul. Deshalb muss der E-Modul für das verwendete Material genau bestimmt werden (z. B. im Zugversuch), während für die Querkontraktion häufig ein ungefährer Wert genügt.

Einflüsse der Zugabe ausgewählter Glasbestandteile auf die Poissonzahl eines speziellen Basisglases.[10]

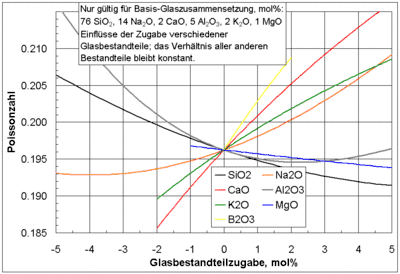
Der Kehrwert der Poissonzahl

In der Geotechnik und Felsmechanik wird auch der Kehrwert der Poissonzahl als „Poissonzahl“ bezeichnet. Oft wird dann das Zeichen ${\displaystyle m}$ verwendet. Eine einheitliche Bezeichnung hat sich bisher nicht durchgesetzt. Zur Vereinheitlichung wäre folgende Regelung empfehlenswert, die Othmar Rescher bereits 1965 vorgeschlagen hat: In seinem Buch Talsperrenstatik: Berechnung und Bemessung von Gewichtsstaumauern bezeichnet er die Querdehnzahl mit ${\displaystyle \nu }$ und die Poisson’sche Konstante mit ${\displaystyle m}$:

• Querdehnzahl: Zeichen: ${\displaystyle \nu }$; mit Zahlenwerten von 0 bis < 0,5
• Poisson’sche Konstante oder „Poissonzahl“ (der Geotechnik); mit Zahlenwerten > 2

wobei gilt:

${\displaystyle \nu ={\frac {1}{m}}}$

Siehe auch

• Elastizitätsmodul
• Schubmodul
• Kompressionsmodul
• Auxetisches Material

Weblinks

• Materialien mit negativen Poissonzahlen (englisch)

Einzelnachweise

1. Wolfgang Demtröder: Experimentalphysik 1: Mechanik und Wärme, 5. Aufl., 2008, S. 173.
2. Dieter Meschede: Gerthsen Physik, 2010, 24. Aufl., S. 140.
3. R. W. Ogden: Non-Linear Elastic Deformations. Dover Publications, Mineola NY 1984.
4. VDI-Richtlinie 2014 Teil 3.
5. Klaas Kölln: Morphologie und mechanische Eigenschaften von Zellulosefasern. Dissertation Uni Kiel (PDF; 2,0 MB) S. 22.
6. G. Mavko, T. Mukerji, J. Dvorkin: The Rock Physics Handbook. Cambridge University Press, 2003, ISBN 0-521-54344-4 (paperback).
7. Matthew A. Hopcroft, William D. Nix, Thomas W. Kenny: What is the Young’s Modulus of Silicon? In: Journal of Microelectromechanical Systems. Band 19, Nr. 2, 2010, S. 229–238, doi:10.1109/JMEMS.2009.2039697.
8. Karl-Heinrich Grote, Jörg Feldhusen: Dubbel Taschenbuch für den Maschinenbau. 23. Auflage. 2011, S. E125.
9. Friedrich Ostermann: Anwendungstechnologie Aluminium. 3. Auflage. Springer Vieweg, Berlin/Heidelberg 2014, ISBN 978-3-662-43807-7, S. 212, doi:10.1007/978-3-662-43807-7 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Januar 2019]).
10. Calculation of the Poisson Ratio for Glasses. Glassproperties.com