Cauchysches Fundamentaltheorem

Das Cauchy’sche Fundamentaltheorem (nach Augustin-Louis Cauchy) besagt, dass der Spannungsvektor T⁽ⁿ⁾, ein Vektor mit der Dimension Kraft pro Fläche, eine lineare Abbildung der Einheitsnormale n der Fläche ist, auf der die Kraft wirkt, siehe Abb. 1. Die lineare Abbildung leistet nach Cauchy ein Spannungstensor, der nur vom Spannungszustand und nicht von der Orientierung n der Schnittfläche abhängt. Cauchy begründete das Fundamentaltheorem mit dem im Folgenden skizzierten Tetraederargument, das sich auf dem Schnittprinzip, dem zweiten Newton’schen Gesetz und dem Cauchy’schen Postulat[1] gründet, wonach der Spannungsvektor nur von der Normale und nicht etwa auch von der Krümmung der Fläche abhängt.

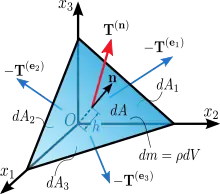
Abb. 1: Der Spannungsvektor T⁽ⁿ⁾ an einer Schnittfläche dA ist eine lineare Funktion des Normalenvektors n

Mit diesem für die Kontinuumsmechanik zentralen Theorem führte Cauchy das wichtigste Hilfsmittel der Kontinuumsmechanik – die Tensorrechnung – ein. Vier fundamentale physikalische Gesetze, die Impuls-, Drehimpuls- und Energiebilanz sowie der zweite Hauptsatz der Thermodynamik in Form der Clausius-Duhem-Ungleichung werden in der Kontinuumsmechanik, in ihrer am materiellen Punkt gültigen Gestalt, mit Hilfe des Spannungstensors formuliert.

Einführung

Betrachtet wird ein Zylinder, an dem zwei, entgegen gesetzte, gleich große Kräfte F auf den Stirnflächen ziehen (1 in Abb. 2), sodass mechanisches Gleichgewicht herrscht.

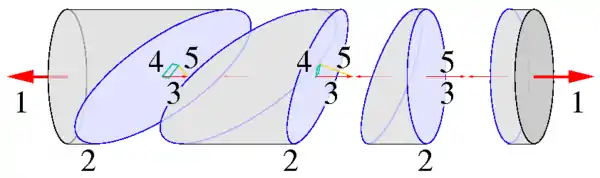
Abb. 2: Zylinder (grau) unter äußerer Belastung (1) mit Schnittebenen (2) und Schnittspannungen (3/ rot), die sich aufteilen in Schubspannungen (4/ grün) und Normalspannungen (5/ gelb)

Die Kräfte (1) sollen die Resultierende eines auf der ganzen Fläche gleichmäßig wirkenden Spannungsvektors sein. Der Zylinder kann nun gedanklich an Schnittflächen (2) zerteilt werden. Weil dies nur gedanklich ausgeführt wird, bleibt jedes Teilstück im Gleichgewicht, weswegen an jeder Schnittfläche wieder gleichmäßig verteilte Spannungsvektoren (3) mit immer gleichgroßer, resultierender Schnittkraft (1) wirken.

Hier ist nun dreierlei festzustellen:

Durch schräge Schnitte vergrößert sich die Schnittfläche, womit sich die Länge (der Betrag) der flächenbezogenen Spannungsvektoren (3) verringert.
Die Spannungsvektoren (3) müssen nicht in Richtung der Normale auf den Schnittflächen liegen, sondern teilen sich auf in Normalspannungen (5) in Normalenrichtung und Schubspannungen (4) in der Schnittfläche senkrecht zur Normalen.
Die Schnittspannungen (4) und (5) sind von der Ausrichtung der Normale der Schnittfläche abhängig.

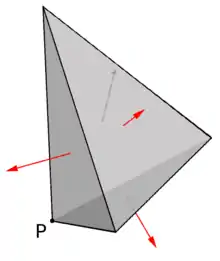
Abb. 3: Vier flächenverteilte Kräfte (Pfeile) am infinitesimal kleinen Tetraeder (grau) müssen sich jederzeit und überall gegenseitig aufheben.

Durch geeignet gelegte Schnitte kann gedanklich aus dem Zylinder ein Tetraeder wie in Abb. 3 herausgetrennt werden. Auch dieser Teilkörper befindet sich, wie der ganze Zylinder, im Gleichgewicht, weswegen sich die Schnittkräfte (rote Pfeile) auf allen vier Flächen in Summe aufheben. Rein geometrisch erweist sich, dass die Normalenvektoren auf den Seitenflächen sich ebenfalls zu null summieren, wenn sie mit dem Inhalt ihrer Dreiecksseite multipliziert werden.

Beide Bedingungen, Nullsumme der Spannungsvektoren und der Normalenvektoren, die jeweils mit dem Flächeninhalt gewichtet werden, lassen sich nur dann bei beliebig gestalteten Tetraedern erfüllen, wenn die Spannungs- und Normalenvektoren linear und unbeeinflusst vom gewählten Bezugssystem voneinander abhängen.

Bezugssysteminvariante lineare Abbildungen leisten Tensoren.

Das Cauchy’sche Fundamentaltheorem fasst diese Aussagen in einer Formel zusammen:[2]

{\vec {t}}={\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}}={\hat {n}}\cdot {\boldsymbol {\sigma }}

.

Darin ist

${\vec {t}}$ der Spannungsvektor, T⁽ⁿ⁾ in Abb. 1, (3) in Abb. 2,
${\boldsymbol {\sigma }}$ der Spannungstensor und ${\boldsymbol {\sigma }}^{\top }$ sein transponierter,
${\hat {n}}$ der Normaleneinheitsvektor, n in Abb. 1, und
„·“ das Skalarprodukt.

Das Tetraederargument gilt nicht nur im Gleichgewicht bei homogenem Spannungszustand, sondern jederzeit und überall in jedem Körper, was im Folgenden detaillierter ausgeführt wird.

Der Tetraeder

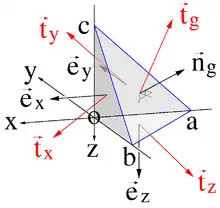
An einem Tetraeder (grau) greifen Schnittspannungsvektoren (rot) an

Cauchy’s Tetraederargument für die Einführung des Spannungstensors kann an einem, aus einem Körper herausgeschnittenen, Tetraeder eingesehen werden, siehe Abbildung rechts. Drei der Flächen des Tetraeders seien parallel zu einer beliebigen Orthonormalbasis ausgerichtet und im Schnittpunkt dieser drei Flächen liege der Ursprung (o im Bild) eines kartesischen Koordinatensystems mit x-, y- und z-Richtungen. Die Kanten des Tetraeders haben vom Ursprung aus gesehen die Längen a, b und c in negativer x-, y- bzw. z-Richtung. So besitzen die Flächen die Flächenelemente (Flächeninhalt mal Normale):

{\vec {a}}_{x}={\frac {bc}{2}}{\vec {e}}_{x}\;,\quad {\vec {a}}_{y}={\frac {ac}{2}}{\vec {e}}_{y}\;,\quad {\vec {a}}_{z}={\frac {ab}{2}}{\vec {e}}_{z}

Das Flächenelement der vierten, schrägen Fläche berechnet sich mit dem Kreuzprodukt „×“:

{\vec {a}}_{g}=|{\vec {a}}_{g}|{\vec {n}}_{g}={\frac {1}{2}}{\begin{pmatrix}-a\\b\\0\end{pmatrix}}\times {\begin{pmatrix}0\\b\\-c\end{pmatrix}}={\frac {1}{2}}{\begin{pmatrix}-bc\\-ac\\-ab\end{pmatrix}}=-{\vec {a}}_{x}-{\vec {a}}_{y}-{\vec {a}}_{z}

Darin ist $|(\cdot )|$ die Frobeniusnorm eines Vektors und ${\vec {n}}_{g}$ der Normalenvektor der Fläche. Die Flächenelemente summieren sich zum Nullvektor.

Das Spannungsprinzip von Euler-Cauchy

Nach dem Spannungsprinzip von Euler-Cauchy existiert auf den Schnittflächen ein Feld von Spannungsvektoren, das die Wirkung des dort weggeschnittenen Teils des Körpers ersetzt, siehe Schnittprinzip. Die Spannungsvektoren haben die Gestalt

{\vec {t}}_{i}=\sum _{j=1}^{3}({\vec {t}}_{i}\cdot {\hat {e}}_{j}){\hat {e}}_{j}=:\sum _{j=1}^{3}\sigma _{ij}{\hat {e}}_{j}\;,\quad i=1,2,3

wenn – wie üblich – die x-, y- und z-Koordinaten mit 1, 2 und 3 durchnummeriert werden. Der erste Index i bezieht sich also auf die Flächennormale und der zweite j auf die Komponente des Spannungsvektors. Bei hinreichend (infinitesimal) kleinem Tetraeder können diese Spannungsvektoren als konstant über die Flächen angenommen werden.

Dem Cauchy’schen Postulat[1] zufolge hängen diese Spannungsvektoren ausschließlich von den Normalenvektoren ${\hat {n}}$ im betreffenden Punkt der Fläche ab und nicht z. B. von deren Krümmung.

Eine Konsequenz hiervon ist das Cauchy’sche Fundamentallemma nach dem auf verschiedenen Seiten derselben Fläche wirkende Spannungsvektoren entgegengesetzt gleich groß sind:

{\vec {t}}(-{\hat {n}})=-{\vec {t}}({\hat {n}})

Dieses Lemma entspricht Newton’s Prinzip von Actio und Reactio.

Das zweite Newton’sche Gesetz

Das zweite Newton'sche Gesetz besagt, dass die am Tetraeder von außen angreifenden Kräfte – neben volumenverteilten Kräften diese mit der Fläche multiplizieren Spannungsvektoren – den Tetraeder beschleunigen. Wenn die Kantenlängen des Tetraeders die Größenordnung L haben, dann sind die Flächen und die mit der Fläche multiplizieren Spannungsvektoren von der Größenordnung L² und das Volumen des Tetraeders hat die Größenordnung L³. Bei infinitesimal kleinen Kantenlängen (mit L → 0) können die dem Volumen und damit der Masse proportionalen Größen (Gewichtskraft, Impulsänderung oder Trägheitskraft) gegenüber den Oberflächenkräften vernachlässigt werden. Also muss am infinitesimal kleinen Tetraeder in allen Raumrichtungen die Summe der Oberflächenkräfte verschwinden. Anders ausgedrückt müssen die Oberflächenkräfte am Tetraeder jederzeit und überall im Gleichgewicht sein.

Der Cauchy’sche Spannungstensor

Summation der in x-, y- und z-Richtung an den Tetraeder angreifenden Oberflächenkräfte liefert:

{\begin{aligned}{\frac {bc}{2}}{\vec {t}}_{x}+{\frac {ac}{2}}{\vec {t}}_{y}+{\frac {ab}{2}}{\vec {t}}_{z}=&{\frac {bc}{2}}{\begin{pmatrix}\sigma _{xx}\\\sigma _{xy}\\\sigma _{xz}\end{pmatrix}}+{\frac {ac}{2}}{\begin{pmatrix}\sigma _{yx}\\\sigma _{yy}\\\sigma _{yz}\end{pmatrix}}+{\frac {ab}{2}}{\begin{pmatrix}\sigma _{zx}\\\sigma _{zy}\\\sigma _{zz}\end{pmatrix}}\\=&\underbrace {\begin{pmatrix}\sigma _{xx}&\sigma _{yx}&\sigma _{zx}\\\sigma _{xy}&\sigma _{yy}&\sigma _{zy}\\\sigma _{xz}&\sigma _{yz}&\sigma _{zz}\end{pmatrix}} _{=:{\boldsymbol {\sigma }}^{\top }}\underbrace {{\frac {1}{2}}{\begin{pmatrix}bc\\ac\\ab\end{pmatrix}}} _{=-{\vec {a}}_{g}}\\=&-{\boldsymbol {\sigma }}^{\top }\cdot {\vec {a}}_{g}=-|{\vec {a}}_{g}|{\boldsymbol {\sigma }}^{\top }\cdot {\vec {n}}_{g}\end{aligned}}

Hier manifestiert sich der Cauchy’sche Spannungstensor

{\boldsymbol {\sigma }}={\begin{pmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{pmatrix}}={\begin{pmatrix}{\vec {t}}_{x}&{\vec {t}}_{y}&{\vec {t}}_{z}\end{pmatrix}}^{\top }=\sum _{i=1}^{3}{\vec {e}}_{i}\otimes {\vec {t}}_{i}

,

in dem die Spannungsvektoren in x-, y- und z-Richtung zeilenweise eingetragen sind[2]. Das Rechenzeichen $\otimes$ bildet das dyadische Produkt von zwei Vektoren.

Zwar ist der Cauchy’sche Spannungstensor symmetrisch, aber das ergibt sich erst aus dem Drallsatz, der hier nicht in die Betrachtung einfließt.

Das Tetraederargument

Nach dem zweiten Newton’schen Gesetz muss, wie oben dargelegt, die Summe aller Kräfte in jeder Raumrichtung verschwinden:

{\begin{aligned}{\frac {bc}{2}}{\vec {t}}_{x}+{\frac {ac}{2}}{\vec {t}}_{y}+{\frac {ab}{2}}{\vec {t}}_{z}+|{\vec {a}}_{g}|{\vec {t}}_{g}=|{\vec {a}}_{g}|(-{\boldsymbol {\sigma }}^{\top }\cdot {\vec {n}}_{g}+{\vec {t}}_{g})={\vec {0}}\;\;\\\rightarrow {\boldsymbol {\sigma }}^{\top }\cdot {\vec {n}}_{g}={\vec {t}}_{g}\end{aligned}}

Wenn also ${\boldsymbol {\sigma }}^{\top }\cdot {\vec {n}}_{g}={\vec {t}}_{g}$ gilt, dann sind die Kräfte im Gleichgewicht.

Nun ist auch umgekehrt

{\begin{aligned}{\vec {0}}=&{\boldsymbol {\sigma }}^{\top }\cdot {\vec {0}}={\boldsymbol {\sigma }}^{\top }\cdot ({\vec {a}}_{x}+{\vec {a}}_{y}+{\vec {a}}_{z}+{\vec {a}}_{g})\\=&{\boldsymbol {\sigma }}^{\top }\cdot {\vec {a}}_{x}+{\boldsymbol {\sigma }}^{\top }\cdot {\vec {a}}_{y}+{\boldsymbol {\sigma }}^{\top }\cdot {\vec {a}}_{z}+{\boldsymbol {\sigma }}^{\top }\cdot {\vec {a}}_{g}\\=&{\frac {bc}{2}}{\boldsymbol {\sigma }}^{\top }\cdot {\hat {e}}_{x}+{\frac {ac}{2}}{\boldsymbol {\sigma }}^{\top }\cdot {\hat {e}}_{y}+{\frac {ab}{2}}{\boldsymbol {\sigma }}^{\top }\cdot {\hat {e}}_{z}+|{\vec {a}}_{g}|{\boldsymbol {\sigma }}^{\top }\cdot {\hat {n}}_{g}\end{aligned}}

Es gilt also auch die Umkehrung: Wenn die Spannungsvektoren die vom Spannungstensor transformierten Normalenvektoren sind, dann herrscht am infinitesimal kleinen Tetraeder Gleichgewicht. Weil die Ausrichtung des Tetraeders und die Schräge seiner vierten Fläche beliebig gewählt werden können, folgt das Cauchy’sche Fundamentaltheorem

{\vec {t}}={\boldsymbol {\sigma }}^{\top }\cdot {\vec {n}}

oder gleichbedeutend

{\vec {t}}={\vec {n}}\cdot {\boldsymbol {\sigma }}

.

Siehe auch

Formelsammlung Tensoralgebra

Fußnoten

Haupt (2000) nennt das Postulat Cauchy’sches Spannungsprinzip
Manchmal, wie in Haupt (2000), wird die transponierte Beziehung
${\vec {t}}={\boldsymbol {\sigma }}^{*}\cdot {\hat {n}}\quad \rightarrow \quad {\boldsymbol {\sigma }}^{*}={\boldsymbol {\sigma }}^{\top }$
benutzt. Dann stimmen die Indizes der Komponenten der Spannungsvektoren an dieser Stelle nicht mit denen der Spannungskomponenten im Cauchy’schen Spannungstensor überein. Weil der Cauchy’sche Spannungstensor aufgrund der Drehimpulsbilanz symmetrisch ist, hat diese Diskrepanz aber keine Auswirkungen.

Literatur

H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5.
P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2000, ISBN 3-540-66114-X.
W. H. Müller: Streifzüge durch die Kontinuumstheorie. Springer, 2011, ISBN 978-3-642-19869-4.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[postulat-1] Haupt (2000) nennt das Postulat Cauchy’sches Spannungsprinzip

[haupt-2] Manchmal, wie in Haupt (2000), wird die transponierte Beziehung
${\vec {t}}={\boldsymbol {\sigma }}^{*}\cdot {\hat {n}}\quad \rightarrow \quad {\boldsymbol {\sigma }}^{*}={\boldsymbol {\sigma }}^{\top }$
benutzt. Dann stimmen die Indizes der Komponenten der Spannungsvektoren an dieser Stelle nicht mit denen der Spannungskomponenten im Cauchy’schen Spannungstensor überein. Weil der Cauchy’sche Spannungstensor aufgrund der Drehimpulsbilanz symmetrisch ist, hat diese Diskrepanz aber keine Auswirkungen.