Solow-Modell
Das Solow-Modell, auch Solow-Swan-Modell oder Solow-Wachstumsmodell genannt, ist ein 1956 von Robert Merton Solow und Trevor Swan entwickeltes Modell, welches einen Beitrag dazu leistet, das ökonomische Wachstum einer Volkswirtschaft mathematisch zu erklären. Es stellt ein exogenes Wachstumsmodell dar und bildet eine Grundlage der neoklassischen Wachstumstheorie. Aufgrund seiner besonderen attraktiven mathematischen Eigenschaften und der mathematischen Einfachheit erwies sich das Solow-Modell als ein geeigneter Ausgangspunkt für verschiedenste Erweiterungen.
Allgemeines
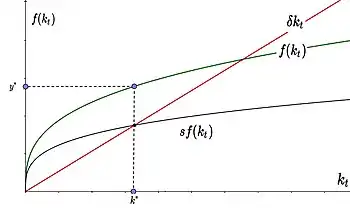
Das Solow-Modell erklärt Wachstum als Prozess der Akkumulation von physischem Kapital hin zu einem langfristigen Gleichgewicht zwischen Investitionen und Abschreibungen, einem sogenannten Wachstumsgleichgewicht bzw. stationären Zustand (englisch steady state). Im Kern des Modells befindet sich eine aggregierte neoklassische Produktionsfunktion, welche meist vom Cobb-Douglas-Typ ist und die dem makroökonomischen Modell erlaubt „Kontakt zu der Mikroökonomie herzustellen“. Eine Volkswirtschaft, die zu Beginn mit wenig Kapital ausgestattet ist, wird in dem Modell zusätzliches Kapital ansparen und dadurch wachsen – anfangs mit hohen, mit zunehmender Kapitalakkumulation dann mit niedrigeren Wachstumsraten –, bis das langfristige Gleichgewicht erreicht wird. Im langfristigen Gleichgewicht ist die Wachstumsrate der Pro-Kopf-Produktion null. Weiteres Wachstum ist nur durch nicht im Modell erklärten (exogenen), technologischen Fortschritt möglich, da dieser die Eigenschaft aufweist, dass er die Beschränkung der abnehmenden Grenzerträge überwindet.
Entstehungsgeschichte
Solow und Swan entwickelten voneinander unabhängig ähnliche Versionen ihres Wachstumsmodells; Solow veröffentlichte seinen Beitrag im Februar 1956 im Quarterly Journal of Economics, Swans Artikel erschien im November in Economic Record. Während zu Beginn auch Swans Artikel auf große fachliche Rezeption stieß – der Beitrag wurde mehrmals in Sammelbände aufgenommen, und Swan wurde als Gastprofessor an verschiedene Universitäten eingeladen – setzte sich langfristig Solows Version des Modells und insbesondere die von ihm gewählte graphische Darstellung durch.[1] Später entwickelte Solow viele Implikationen und Anwendungen dieses Modells und erhielt im Jahr 1987 den Wirtschaftsnobelpreis für seine Beiträge zur Wachstumstheorie.[2]
Das Solow-Swan-Modell war eine Kritik und Weiterentwicklung des zu dieser Zeit vorherrschenden Wachstumsmodells nach Harrod-Domar. Wie das Solow-Modell nahm auch das Harrod-Domar-Modell eine konstante, exogene Sparquote an. Das Modell beruhte aber auch auf einer konstanten Grenzproduktivität des Kapitals und auf einer Produktionsfunktion mit geringer bzw. nicht existenter Substituierbarkeit zwischen Arbeit und Kapital. Das Harrod-Domar-Modell erlaubt mehrere verschiedene Wachstumsgleichgewichte: In einem möglichen Szenario wächst Kapital, ohne benutzt zu werden, in einem anderen wächst die Arbeitslosigkeit. Nur in einer Parameterkonstellation ergibt sich ein Wachstumsgleichgewicht, in dem alle verfügbaren Produktionsfaktoren benutzt werden.[3]
Das Modell
Annahmen
Die Volkswirtschaft wird im Solow-Modell als eine Aggregatseinheit angesehen (sozusagen als ein einziger Haushalt), die jegliche Produktions- und Konsumaktivität vornimmt. Weiterhin wird von der Existenz eines Staates abstrahiert und man nimmt an, dass keine monetären Effekte vorliegen, d. h. alle Güterpreise sind auf 1 normiert . Die Volkswirtschaft besitzt zu jedem Zeitpunkt [4] gewisse Mengen an Kapital (), Arbeit () und Technologie (), aus denen zusammen gemäß einer Produktionsfunktion (), Output () produziert wird:[5]
Das Produkt wird dabei als effektive Arbeit bezeichnet. Für die Produktionsfunktion wird angenommen, dass sie neoklassisch ist, also folgende vier Eigenschaften aufweist:
- Essentialität der Produktionsfaktoren. Ein Produktionsfaktor wird als essentiell bezeichnet, wenn ohne dessen Einsatz der Output stets 0 beträgt:
- Konstante Skalenerträge bzw. Homogenität vom Grad 1 in effektiver Arbeit und Kapital. Ökonomisch bedeutet dies: Ein vermehrter/verminderter Einsatz dieser Produktionsfaktoren führt zu einer im gleichen Verhältnis erhöhten/verminderten Produktion:
- Positive und abnehmende Grenzerträge:Die Grenzerträge von Kapital und effektiver Arbeit sind positiv, sinken aber mit zunehmendem Einsatz des jeweiligen Faktors. Wird also beispielsweise mehr effektive Arbeit verwendet, so steigt die Produktion, aber sie steigt weniger, wenn bereits viel effektive Arbeit eingesetzt wird. Mathematisch bedeutet dies, dass die ersten partiellen Ableitungen der Produktionsfunktion nach effektiver Arbeit und Kapital positiv, die jeweiligen zweiten Ableitungen aber negativ sind:
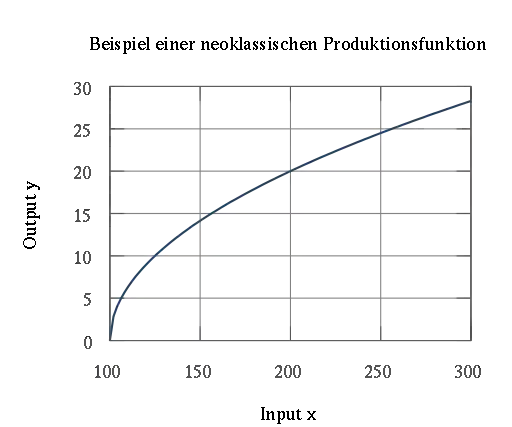 Durch die Annahmen implizierter Verlauf der Produktionsfunktion.
Durch die Annahmen implizierter Verlauf der Produktionsfunktion. - Die sogenannten Inada-Bedingungen[6] müssen erfüllt sein, d. h., dass das Grenzprodukt eines jeden Produktionsfaktors gegen unendlich konvergiert, wenn man nur den jeweiligen Faktoreinsatz gegen null streben lässt. Lässt man den jeweiligen Faktoreinsatz hingegen gegen unendlich streben, so konvergiert das Grenzprodukt des Faktors gegen null:
Ökonomisch bedeutet dies, dass bei gegebener Technologie in einer Volkswirtschaft der Output nicht beliebig gesteigert werden kann, indem der Arbeitseinsatz (bzw. Kapitaleinsatz) immer weiter erhöht wird. Somit ist eine positive Wachstumsrate des Einkommens im Falle einer neoklassischen Produktionsfunktion ohne technischen Fortschritt bei Gültigkeit der Inada-Bedingungen langfristig nicht möglich.
In seiner einfachsten Form bezieht sich das Solow-Modell außerdem auf eine geschlossene Volkswirtschaft ohne Staatstätigkeit. Einkommen und Produktion müssen sich in einer solchen Volkswirtschaft entsprechen, die Produktion kann deswegen entweder für Konsum oder für Investitionen verwendet werden (Outputverwendungsgleichung):
Die Bruttoinvestitionen entsprechen ex post außerdem genau dem, was die Volkswirtschaft spart: (Siehe hierzu auch Investition und Sparen). In einer geschlossenen Volkswirtschaft ist somit . Das Sparverhalten der Volkswirtschaft wird durch eine konstante Sparquote () modelliert: , wobei zwischen 0 und 1 liegt. Die Volkswirtschaft spart also in jeder Periode einen gewissen Prozentsatz der gesamten Produktion. Diese über die Zeit konstante Sparquote wird als ein nicht im Modell bestimmter, exogener Parameter angenommen. Die Resultate zusammengefasst gilt:
- mit
Zwei weitere Annahmen betreffen Kapital und Arbeit: Hinsichtlich Kapital wird angenommen, dass in jeder Periode ein gewisser Prozentsatz des bestehenden Kapitals unbrauchbar wird (Abschreibungen), während die arbeitende Bevölkerung mit einer konstanten Wachstumsrate exponentiell wächst.[7] Weiterhin wird angenommen, dass die Sparquote , aufgrund der unterstellten Gleichheit von Sparen und Investitionen, der Investitionsquote entspricht. Dies ist jedoch keine restriktive Annahme, da in der Realität eine annähernde Gleichheit der beiden Quoten über die Zeit herrscht.
Der Wachstumsprozess
Zur Analyse von Volkswirtschaften mit wachsender Bevölkerung und zur besseren Vergleichbarkeit von Volkswirtschaften unterschiedlicher Größe werden die Modellgrößen nicht absolut, sondern pro Kopf ausgedrückt, wobei Kleinbuchstaben für Pro-Kopf-Größen verwendet werden. Man definiert demgemäß:
- ,
wobei die letzte Gleichung aus der Annahme konstanter Skalenerträge folgt.
Unter der Annahme einer konstanten Technologie kann dann mit dem Pro-Kopf-Kapital die Pro-Kopf-Produktionsfunktion definiert werden als[8][9]
- .
Diese gibt für jeden Pro-Kopf-Kapitalbestand an, wie viel Output pro Kopf hergestellt wird. Für die Entwicklung des Pro-Kopf-Einkommens ist also der Pro-Kopf-Kapitalbestand entscheidend.
Dessen Entwicklung wird durch drei Faktoren bestimmt:
- In jeder Periode spart die Volkswirtschaft einen Teil ihres Pro-Kopf-Einkommens:
- In jeder Periode wird ein Teil des Pro-Kopf-Kapitalstocks: unbrauchbar
- In jeder Periode wächst die Bevölkerung exponentiell mit einer exogenen Rate , sodass mehr Arbeiter mit Kapital ausgestattet werden müssen, um das Pro-Kopf-Kapital konstant zu halten:
Damit ist die Veränderung des Pro-Kopf-Kapitalstocks jeder Periode gegeben als
Fundamentale Bewegungsgleichung des Solow-Modells mit Bevölkerungswachstum:[10]
- : Änderung der Kapitalintensität über die Zeit
- : Bruttoinvestitionen pro Kopf
- : Erweiterte Abschreibungen pro Kopf
- : Nettoinvestitionen pro Kopf
Wenn positiv ist, wächst der Pro-Kopf-Kapitalstock und damit das Pro-Kopf-Einkommen. Ist negativ, so schrumpfen Pro-Kopf-Kapital und -Produktion. Formal bedeutet dies:
- (Kapitalintensität und Pro-Kopf-Einkommen wachsen)
- (Kapitalintensität und Pro-Kopf-Einkommen schrumpfen)
Im langfristigen Gleichgewicht – dem Wachstumsgleichgewichts-Niveau der Volkswirtschaft – muss gelten, dass die Investitionen genau den Abschreibungen (unter Berücksichtigung des Bevölkerungswachstums) des Kapitalmodells entsprechen, d. h., der Kapitalbestand pro Kopf ist über die Zeit konstant ():
Der Pro-Kopf-Kapitalstock , der diese Gleichung erfüllt, ist der Wachstumsgleichgewichts-Kapitalstock () der Volkswirtschaft.[11] Die oben genannten Annahmen an die Produktionsfunktion (konstante Skalenerträge, positive, abnehmende Grenzerträge und die Inada-Bedingungen) garantieren die Existenz eines eindeutigen Wachstumsgleichgewichts.[12]
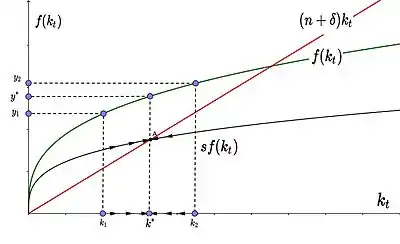
Graphisch kann dies in einem Diagramm mit Pro-Kopf-Kapital auf der horizontalen und Pro-Kopf-Einkommen auf der vertikalen Achse dargestellt werden: ist gemäß der Annahmen eine konkave Funktion, ebenso die volkswirtschaftliche Sparfunktion . Die -Kurve ist eine Gerade, die angibt, wie viel gespart werden muss, um den Pro-Kopf-Kapitalstock gerade konstant zu halten und wird deswegen auch als Investitionsbedarfslinie (englisch requirement line) bezeichnet. Der Schnittpunkt zwischen Sparfunktion und Investitionsbedarfslinie bestimmt das langfristige Gleichgewichtsniveau (Wachstumsgleichgewicht) des Kapitalstocks, bei dem gerade so viel gespart wird, dass der Kapitalstock trotz Abschreibungen und Bevölkerungswachstum konstant bleibt. Wenn dieser Kapitalstock erreicht wird, ist die Wachstumsrate null und Pro-Kopf-Produktion, -Einkommen und -Kapital sind über die Zeit konstant.[13]
Falls das Pro-Kopf-Kapital unter dem langfristigen Gleichgewichtsniveau liegt, wird die Volkswirtschaft wachsen und das langfristige Gleichgewicht schließlich asymptotisch erreichen. Die Wachstumsrate geht dabei mit steigendem Kapitalstock immer weiter zurück – eine Implikation der Annahme, dass die Grenzerträge des Kapitals abnehmen.[14] Das Solow-Modell sagt also voraus, dass, ceteris paribus, Volkswirtschaften mit niedrigerem Pro-Kopf-Kapitalstock schneller wachsen als solche mit hoher Kapitalausstattung.[15]
Konvergenz zum Gleichgewicht
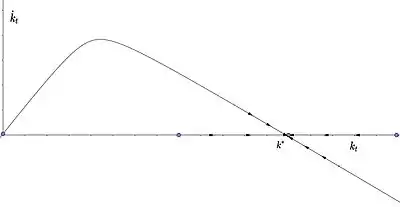
In dem Bereich, in dem die Investitionen () größer als die Abschreibungen () sind, sind die Nettoinvestitionen positiv und somit steigt die Kapitalintensität über die Zeit [16]. Im Gegensatz dazu sind die Nettoinvestitionen in dem Bereich, in dem die Investitionen kleiner als die Abschreibungen sind, negativ und somit sinkt die Kapitalintensität über die Zeit . Folglich ist das System global stabil, d. h., für jeden beliebigen Anfangswert () konvergiert die Ökonomie zum Wachstumsgleichgewicht () (globale Stabilität):
Änderungen exogener Parameter
Der langfristige Wachstumsgleichgewichts-Kapitalstock () wird, wie oben ausgeführt, bestimmt durch[17]
- .
Dabei werden die Sparquote , die Abschreibungsquote und das Bevölkerungswachstum als exogene, nicht im Modell bestimmte Parameter angesehen. Änderungen dieser Parameter haben jedoch Auswirkungen auf das langfristige Gleichgewicht der Volkswirtschaft.
Bevölkerungswachstum und Abschreibungen
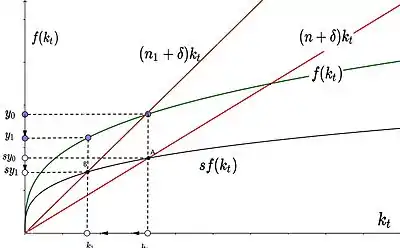
Ein schnelleres Bevölkerungswachstum (größeres ) oder größere Abschreibungen (größeres ) haben im Modell die gleichen Auswirkungen auf das langfristige Gleichgewichtsniveau: Sie erhöhen die Steigung der Investitionsbedarfslinie und senken dadurch Pro-Kopf-Kapitalstock und -Einkommen: In jeder Periode müssen mehr Arbeiter mit Kapital ausgestattet (bzw. muss mehr Kapital ersetzt) werden, sodass bei gleichem Sparverhalten und gleicher Produktionstechnologie weniger Pro-Kopf-Kapital gebildet wird.[18] Abb. 3 zeigt graphisch, wie das langfristige Gleichgewicht auf ein erhöhtes Bevölkerungswachstum reagiert: Die schwarze Sparfunktionslinie bleibt unverändert, die Investitionsbedarfslinie mit Steigung (rot) rotiert um den Ursprung. Das neue langfristige Gleichgewicht resultiert aus dem Schnittpunkt der veränderten Investitionsbedarfslinie mit der Sparfunktion und ist durch ein geringeres Pro-Kopf-Kapital und -Einkommen charakterisiert als das vorherige Gleichgewicht . Da die neue Investitionsbedarfslinie beim Kapitalbestand höher liegt als , wird zu wenig Kapital angespart – die Wirtschaft schrumpft (). Dieser Prozess setzt sich fort, bis das neue Gleichgewichtsniveau in Punkt (Schnittpunkt der neuen Investitionsbedarfslinie mit der Sparenkurve: ) erreicht wird. Im neuen Gleichgewicht liegt ein gleichgewichtiger geringer Pro-Kopf-Kapitalstock vor und ein geringeres gleichgewichtiges Pro-Kopf-Outputniveau wird realisiert.
Sparquote und Goldene Regel der Akkumulation
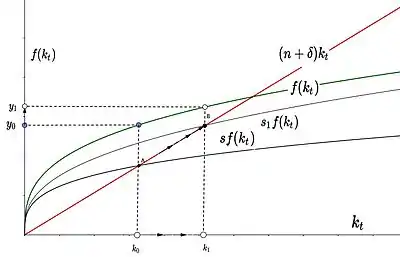
Eine Erhöhung der Sparquote schiebt die Sparkurve der Volkswirtschaft nach oben, was dazu führt, dass der Wachstumsgleichgewicht-Pro-Kopf-Kapitalstock ansteigt und damit auch das Pro-Kopf-Einkommen. Abb. 4 veranschaulicht dies graphisch: Die Erhöhung der Sparquote verschiebt die Sparfunktion von ihrer ursprünglichen Lage (schwarz) nach oben, während die Investitionsbedarfslinie (rot) unverändert bleibt. Das neue Gleichgewicht ergibt sich aus dem Schnittpunkt der Investitionsbedarfslinie mit der neuen Sparfunktion und weist pro Kopf einen größeren Kapitalstock und höheres Einkommen auf.
Der Effekt einer solchen Erhöhung auf den Konsum ist aber nicht eindeutig: Einerseits wird im langfristigen Gleichgewicht mehr produziert, andererseits ist mit höherer Sparquote aber der Pro-Kopf-Konsum niedriger. Graphisch entspricht der Pro-Kopf-Konsum für gegebenes Pro-Kopf-Kapital dem vertikalen Abstand zwischen der Produktionsfunktion und der Sparfunktion am gleichen Pro-Kopf-Kapital; In Abb. 4 ist dies der vertikale Abstand zwischen der roten und der grünen Linie. Dies zeigt, warum der Effekt auf den Konsum grundsätzlich unbestimmt ist: Zwar weist das neue Gleichgewicht in Punkt eine höhere Produktion pro Kopf auf, die neue Sparfunktion liegt jedoch auch näher an der Produktionsfunktion.
Die Goldene Regel der Akkumulation beschreibt diejenige Sparquote in einer Volkswirtschaft, durch die der Konsum im stationären Zustand maximiert wird:
- .[19]
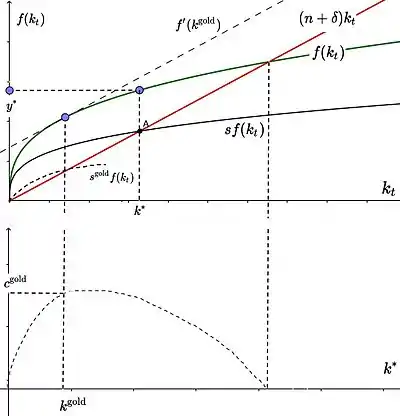
Für jede Sparquote muss im langfristigen Gleichgewicht gelten, dass . Gleichzeitig ist das zum Gleichgewicht gehörige Konsumniveau gegeben durch . Aus diesem Grund kann der gleichgewichtige Konsum als Funktion der Sparquote beschrieben werden:
Dies kann dann über maximiert werden und ergibt die Bedingung erster Ordnung (notwendige Bedingung):
- ,
wobei , sodass die Bedingung vereinfacht werden kann zu bzw. (Netto-Grenzprodukt des Kapitals entspricht der Bevölkerungswachstumsrate). Der Kapitalstock , der diese Gleichung erfüllt, und die zugehörige Sparquote maximieren den langfristigen Gleichgewichtskonsum der Volkswirtschaft (siehe Abb. 5).[20] Obwohl die auf diese Art gefundene Sparquote den Gleichgewichtskonsum maximiert, ist nicht klar, ob dies aus der Sicht einer Volkswirtschaft wünschenswert ist. Für eine Volkswirtschaft, die sich mit in einem Gleichgewicht befindet, bedeutet eine Erhöhung der Sparquote auf zwar ein langfristig höheres Konsumniveau, dies aber erst, wenn das neue Gleichgewicht erreicht wird.
In den ersten Perioden nach der Erhöhung der Sparquote würde sich der Konsum aber zunächst reduzieren (da die Sparquote erhöht wird, aber noch nicht genug Kapital für das neue Wachstumsgleichgewicht gebildet wurde und dadurch die Produktion im Vergleich zum neuen Wachstumsgleichgewicht noch niedrig ist). Je nachdem, wie viel Gewicht die Volkswirtschaft auf heutigen gegenüber zukünftigem Konsum legt, könnte es also nicht wünschenswert sein, die Sparquote heute zu erhöhen (kurze Frist), um dafür in der langen Frist ein neues Gleichgewicht mit höherem Konsum zu erreichen. Anders liegt der Fall, wenn die derzeitige Sparquote ist. In diesem Falle könnte ein Gleichgewicht mit höherem Konsum erreicht werden, indem die Sparquote reduziert, also mehr konsumiert würde. Die Volkswirtschaft würde dadurch im neuen Gleichgewicht und auch in den Perioden davor immer mehr konsumieren. Eine Situation mit wird deswegen als dynamisch ineffizient bezeichnet.[21]
Abb. 6 und Abb. 7 zeigen graphisch, wie sich unterschiedliche Veränderungen in der Sparquote auswirken können. In Abb. 6 erhöht sich die Sparquote ausgehend von einem ursprünglichen, dynamisch effizienten Gleichgewicht. Die Erhöhung führt zu positivem Kapitalwachstum und damit zu steigendem Kapital und Einkommen pro Kopf. Das Kapitalwachstum nimmt mit zunehmender Kapitalakkumulation ab und geht asymptotisch gegen null, die Volkswirtschaft erreicht ein neues Gleichgewicht mit höherem Kapital, Einkommen und Konsum pro Kopf. Zu Beginn des Prozesses muss dieses langfristig höhere Niveau jedoch mit niedrigerem Konsum „erkauft“ werden. Ob eine solche Änderung der Sparquote aus Sicht der Volkswirtschaft wünschenswert ist, hängt also davon ab, wie der frühe Konsumverlust gegenüber dem späteren Konsumgewinn bewertet wird. In Abb. 7 wird die Sparquote ausgehend von einer dynamisch ineffizienten, also zu hohen Sparquote gesenkt. Die Senkung führt zu negativem Kapitalwachstum und damit zu sinkendem Kapital und Einkommen pro Kopf. Die Kapitalverringerung nimmt mit zunehmender Kapitalakkumulation ab und geht asymptotisch gegen null, die Volkswirtschaft erreicht ein neues Gleichgewicht mit niedrigerem Kapital und Einkommen pro Kopf. Der langfristige Konsum pro Kopf ist jedoch höher, da weniger gespart wird. Der zentrale Unterschied zur dynamisch effizienten Situation ist, dass der Konsum nicht nur langfristig höher ist, sondern in jeder Periode ab der Erhöhung. Die Volkswirtschaft kann durch eine Senkung der Sparquote also nicht nur langfristig mehr konsumieren, sondern sofort. Unabhängig von der Bewertung frühen gegenüber späteren Konsums ist bei einer Sparquote oberhalb der „goldenen“ Sparquote eine Senkung der Sparquote aus Sicht der Volkswirtschaft also auf jeden Fall wünschenswert.
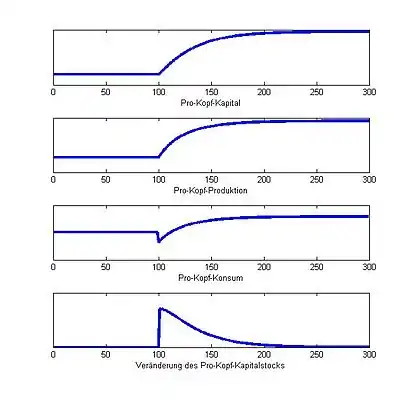 Abb. 6. Erhöhung der Sparquote ausgehend von einer dynamisch effizienten Situation. Auf der jeweiligen vertikalen Achse sind die angegebenen Größen dargestellt, die horizontale Achse gibt die Zeit an. Die Veränderung der Sparquote erfolgt in Zeitperiode .
Abb. 6. Erhöhung der Sparquote ausgehend von einer dynamisch effizienten Situation. Auf der jeweiligen vertikalen Achse sind die angegebenen Größen dargestellt, die horizontale Achse gibt die Zeit an. Die Veränderung der Sparquote erfolgt in Zeitperiode .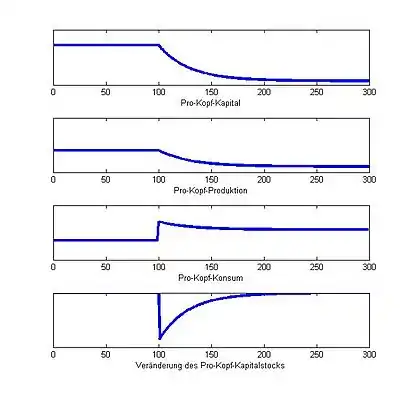 Abb. 7. Senkung der Sparquote ausgehend von einer dynamisch ineffizienten Situation. Auf der jeweiligen vertikalen Achse sind die angegebenen Größen dargestellt, die horizontale Achse gibt die Zeit an. Die Veränderung der Sparquote erfolgt in Zeitperiode .
Abb. 7. Senkung der Sparquote ausgehend von einer dynamisch ineffizienten Situation. Auf der jeweiligen vertikalen Achse sind die angegebenen Größen dargestellt, die horizontale Achse gibt die Zeit an. Die Veränderung der Sparquote erfolgt in Zeitperiode .
Technologischer Fortschritt
Technologischer Fortschritt verschiebt die Produktionsfunktion und damit auch die Sparfunktion im -Diagramm nach oben; der neue Schnittpunkt mit der Investitionsbedarfslinie befindet sich damit bei einem höheren Pro-Kopf-Kapital und -Einkommensniveau. Technologischer Fortschritt kann damit also auch im langfristigen Gleichgewicht zu Wachstum führen.[22][23]
Mit technologischem Fortschritt, der den Produktionsfaktor Arbeit multipliziert, und unter den in Abschnitt 1.1 dargestellten Annahmen kann die Produktionsfunktion durch den Faktor geteilt werden. Dies ergibt anstatt der bisher verwendeten Pro-Kopf-Produktion die Produktion pro effektiver Arbeitseinheit (pro Effizienzeinheit) in Abhängigkeit vom Kapitalstock pro effektiver Arbeitseinheit:
Der Investitionsbedarf pro effektiver Arbeitseinheit ergibt sich wie bisher aus der Abschreibungsrate und dem Wachstum der Bevölkerung; nun muss aber zusätzlich auch die infolge technologischen Fortschritts gestiegene Arbeitsproduktivität ausgeglichen werden: Technologischer Fortschritt führt zu einem Anstieg der effektiven Arbeitseinheiten (das Produkt steigt), das Kapital pro effektiver Arbeitseinheit sinkt also ceteris paribus. Unter der Annahme eines exponentiellen Technologiewachstums mit Wachstumsrate ergibt sich die Investitionsbedarfslinie für Kapital pro effektiver Arbeitseinheit als . Die Bewegungsgleichung für das Kapital pro effektiver Arbeitseinheit lautet damit:
Fundamentale Bewegungsgleichung des Solow-Modells mit Bevölkerungswachstum und technologischem Fortschritt:[24]
Das langfristige Gleichgewicht ist erreicht, wenn der Kapitalstock pro effektiver Arbeitseinheit konstant ist, wenn also gilt:
Der Kapitalstock und damit auch das Einkommen pro effektiver Arbeitseinheit wachsen im langfristigen Gleichgewicht nicht. Das Pro-Kopf-Einkommen ist jedoch gegeben durch
- .
Es wächst also mit der gleichen Rate wie die Technologie der Volkswirtschaft, . Ein Wachstum der Pro-Kopf-Größen im langfristigen Gleichgewicht ist also möglich, allerdings nur aufgrund exogenen technologischen Fortschritts.[25]
Beispiel: Solow-Modell mit Cobb-Douglas-Produktionsfunktion
Eine mögliche Produktionsfunktion, die die oben dargestellten Annahmen erfüllt, stellt folgende Cobb-Douglas-Funktion dar:
- mit
Zu jedem Zeitpunkt wird in der Volkswirtschaft unter dem Einsatz der Produktionsfaktoren Arbeit und Kapital mithilfe eines gegebenen Technologielevels Output produziert. Für die Produktionselastizität des Kapitals gilt die Beschränkung, dass sie zwischen und liegen muss. So folgt für die Produktionselastizität der Arbeit die selbige Beschränkung. Nachdem man die Produktionsfunktion durch die Bevölkerungsgröße teilt, ergibt sich die Pro-Kopf-Version . Die Bewegungsgleichung des Pro-Kopf-Kapitalstockes (Kapitalakkumulationsgleichung) ist dann gegeben durch
- .
Das langfristige Gleichgewicht ergibt sich, wenn diese Veränderung null beträgt und folglich
- ,
und damit gilt für die gleichgewichtige Kapitalintensität dann
- .
Für das gleichgewichtige Pro-Kopf-Einkommen folgt somit
und für den Pro-Kopf-Konsum im stationären Zustand () gilt somit
- .
Anhand der Gleichung von lässt sich erkennen, dass Unterschiede in , also Unterschiede im Technologielevel, der Sparquote, der Abschreibungsrate, der Wachstumsrate der Bevölkerung und der Produktionselastizität des Kapitals die Unterschiede im Pro-Kopf-Einkommen zwischen den Ländern (zumindest teilweise) erklären können. Wegen führen eine größere Sparquote und ein höheres Technologieniveau zu einem höheren gleichgewichtigen Kapitalstock, schnelleres Bevölkerungswachstum und eine größere Abschreibungsrate dagegen zu einem niedrigeren Gleichgewicht.
Weiterhin kann man zeigen, dass obige Produktionsfunktion die genannten Annahmen unter 1.1 erfüllt:
1. Konstante Skalenerträge:
Die Eigenschaft der konstanten Skalenerträge ist erfüllt:
2. Positive und abnehmende Grenzerträge:
Die Grenzprodukte des Kapitals und der Arbeit sind positiv:
Da die partiellen Ableitungen aufgrund der Beschränkung nur positiv werden können, sieht man, dass der Output bei einer Erhöhung der jeweiligen Inputfaktoren steigt. Die partiellen Ableitungen 2. Ordnung ergeben:
Sie werden für alle Inputs negativ sein, also fallen die Zuwachsraten (es liegen abnehmende Grenzerträge vor). Man könnte also sagen, dass bei steigendem Input der Output unterproportional steigt.
3. Die Inada-Bedingungen sind erfüllt:
Die Inada-Bedingungen (zusammen mit den oben genannten Annahmen) implizieren, dass für genau ein stabiles Gleichgewicht mit existiert, bei dem also der Kapitalstock über die Zeit konstant ist.
Verschiedene Sparquoten
Im Folgenden soll anhand einer komparativ statischen Analyse gezeigt werden, wie die Sparquote das Pro-Kopf-Einkommen des jeweiligen Landes determiniert. Für den Vergleich werden zwei Länder herangezogen, die sich in ihrer Sparquote stark unterscheiden, z. B. Korea und Uganda. Man geht im Fall von Korea von einer geschätzten Sparquote von und im Fall von Uganda von einer geschätzten Sparquote von aus. Des Weiteren wird von einer Kapitaleinkommensquote von ausgegangen (empirisch gesehen liegt die Kapitaleinkommensquote in den meisten Ländern etwa bei ). Um zu zeigen, welche Auswirkungen sich für das Pro-Kopf-Einkommen ergeben, wenn sich die beiden Länder nur in der Sparquote unterscheiden, setzt man die gleichgewichtige Pro-Kopf-Einkommen der beiden Länder ins Verhältnis (komparative Statik):
Für das oben genannte Beispiel ergibt sich somit:
Laut dem Solow-Modell ist Korea also doppelt so reich wie Uganda. Tatsächlich ist Korea aber ca. 13-mal so reich. Folglich können Einkommensunterschiede nur zum Teil durch das Solow-Modell erklärt werden.
Empirische Anwendungen
Wachstumsbuchhaltung
Eng mit dem Solow-Modell verbunden ist die sogenannte Wachstumsbuchhaltung[26] (englisch growth accounting), die von Moses Abramovitz[27] und Robert Solow[28] vorangetrieben wurde.[29] Dabei wird untersucht, welcher Anteil des Wirtschaftswachstums durch Kapital, Arbeit und andere Faktoren erklärt werden kann. Für eine allgemeine Produktionsfunktion der Form kann gezeigt werden,[30] dass das Wachstum der Gesamtproduktion aufgeteilt werden kann mittels[31]
- ,
wobei die Elastizität der Produktion in Bezug auf das Kapital angibt. Auf diese Weise kann das Wirtschaftswachstum pro Kopf aufgeteilt werden in Pro-Kopf-Wachstum aufgrund von Pro-Kopf-Kapitalakkumulation und einen weiteren additiven Term , das sogenannte Solow-Residuum. Dieses wird manchmal als Beitrag des technologischen Fortschritts zum Wachstum gedeutet, ist aber tatsächlich ein Sammelterm für alle Faktoren, die zu Wirtschaftswachstum führen und nicht bereits durch die Kapitalakkumulation abgedeckt sind.[32]
Konvergenz
Falls sich die Volkswirtschaft noch unter dem langfristigen Gleichgewichtsniveau befindet und wächst, ist ihre Wachstumsrate höher, je niedriger der Pro-Kopf-Kapitalstock ist. Eine Volkswirtschaft mit ursprünglich wenig Pro-Kopf-Kapital wird gemäß dem Solow-Modell also zunächst sehr hohe Wachstumsraten aufweisen, die dann mit zunehmender Kapitalakkumulation abnehmen und schließlich gegen 0 tendieren. Für zwei Volkswirtschaften mit gleicher Technologie und gleichen exogenen Parametern (Abschreibungsquote, Sparquote, Bevölkerungswachstum) und damit gleichem langfristigen Gleichgewicht, aber unterschiedlicher ursprünglicher Kapitalausstattung, sagt das Modell voraus, dass die ursprünglich ärmere Volkswirtschaft schneller wachsen und damit gegenüber der ursprünglich reicheren Volkswirtschaft „aufholen“ wird (Aufholeffekt). Dieser Prozess wird auch als „-Konvergenz“ bezeichnet.
Absolute Konvergenz
Die absolute Konvergenz sagt aus, dass zwei Länder mit verschiedenen BIP und Kapital pro Kopf Startleveln, aber mit gleichen Leveln bei der Sparquote, Abschreibungsrate, Populationswachstumsrate und der Rate des technischen Fortschritts in der langen Frist zum gleichen Level des Kapitalstocks und BIP pro Kopf konvergieren (Länder mit anfänglich geringerem Einkommenlevel wachsen aufgrund abnehmender Grenzerträge schneller). Zusammenfassend wachsen Länder umso schneller, je weiter sie sich von ihrem spezifischen langfristigen Gleichgewicht entfernt befinden. Eine Vorhersage des Modells wäre also nicht, dass arme Länder schneller wachsen als reiche, sondern dass unter „ähnlichen“ Ländern (Länder die ähnliche Parameter aufweisen) die ursprünglich ärmeren höhere Wachstumsraten aufweisen. Tatsächlich besteht zwischen den OECD-Ländern eine negative Korrelation zwischen ihrem Pro-Kopf-Einkommen 1960 und der durchschnittlichen jährlichen Wachstumsrate zwischen 1960 und 2000. Eine noch deutlichere negative Korrelation besteht zwischen dem Pro-Kopf-Einkommen der Bundesstaaten der USA 1880 und ihren jährlichen Wachstumsraten zwischen 1880 und 2000.[33] Das Solow-Modell sagt jedoch keine absolute Konvergenz vorher, bei der alle armen Länder gleichermaßen aufholen und gegen dasselbe langfristige Gleichgewicht konvergieren. Die Hypothese des Solow-Modells ist stattdessen die der bedingten Konvergenz.
Bedingte Konvergenz
Im Solow-Modell konvergieren Ökonomien zu unterschiedlichen stationären Zuständen, sofern diese Unterschiede in den Modellparametern aufweisen. Wenn sich Länder in der totalen Faktorproduktivität, der Sparquote oder der Abschreibungsrate unterscheiden, unterscheiden sie sich folglich in ihrem langfristigen Gleichgewicht (verschiedene regionale stationäre Zustände). Oft liegt empirisch statt der absoluten die bedingte Konvergenz vor.
Empirische Resultate
Ein weiterer Test auf Konvergenz wurde von N. Gregory Mankiw, David Romer und David N. Weil 1992 durchgeführt.[34] Basierend auf einer Stichprobe von 98 Ländern zeigten sie, dass es keine Korrelation zwischen dem Pro-Kopf-Einkommen 1960 und der Wachstumsrate zwischen 1960 und 1985 gab, also keine absolute Konvergenz. Wenn aber für die Investitionsquote und das Bevölkerungswachstum statistisch kontrolliert wird, zeigt sich ein negativer Effekt des ursprünglichen Einkommensniveaus, was die Hypothese bedingter Konvergenz unterstützt. Das Standard-Solow-Modell überschätzt dabei indes die Geschwindigkeit der Konvergenz, das tatsächliche Aufholen geschieht langsamer als vom Modell vorhergesagt. Mankiw, Romer und Weil konnten allerdings zeigen, dass ein um Humankapital als dritten Produktionsfaktor erweitertes Solow-Modell in etwa jene Konvergenzgeschwindigkeit vorhersagt, die auch in den Daten sichtbar ist. In diesem erweiterten Modell weist die Produktionsfunktion auch den Faktor Humankapital auf und lautet:
- mit .
Das Humankapital pro effektiver Arbeitseinheit entwickelt sich nach einer Bewegungsgleichung ähnlich jener für das Kapital pro effektiver Arbeitseinheit:
- ,
wobei die (ebenfalls exogene) Investitionsquote für Humankapital bezeichnet. Im Wachstumsgleichgewicht sind dann Kapital und Humankapital pro effektiver Arbeitseinheit konstant.
Internationale und historische Einkommensunterschiede
Gemäß dem Solow-Modell gibt es zwei mögliche Gründe für Pro-Kopf-Einkommensunterschiede zwischen Volkswirtschaften: einen unterschiedlichen Pro-Kopf-Kapitalstock und unterschiedliche Arbeitsproduktivität. Tatsächlich kann jedoch der Pro-Kopf-Kapitalstock die großen Einkommensunterschiede zwischen armen und reichen Ländern heute oder zwischen entwickelten Ländern früher und heute nicht erklären. Das Pro-Kopf-Einkommen industrialisierter Länder ist heute etwa zehnmal größer als ein Jahrhundert zuvor; die natürlichen Logarithmen der Pro-Kopf-Einkommen heute und vor Jahren unterscheiden sich also um . Mit der Definition der Elastizität des Pro-Kopf-Einkommens in Bezug auf das Pro-Kopf-Kapital, , folgt . Mit folgt, dass die Differenz im Pro-Kopf-Kapitalstock
betragen muss. Empirische Studien legen nahe, dass rund ein Drittel beträgt. Wenn das Pro-Kopf-Kapital die einzige Quelle für Pro-Kopf-Einkommensunterschiede wäre, müsste das Pro-Kopf-Kapital in den letzten Jahren also etwa um einen Faktor gewachsen sein, um ein Wachstum des Pro-Kopf-Einkommens um den Faktor zu erklären. Tatsächlich ist das Pro-Kopf-Kapital aber nur um etwa einen Faktor gewachsen. Das Wachstum des Pro-Kopf-Kapitals kann den Umfang des Wirtschaftswachstums über die vergangenen Jahre also nicht erklären.[35]
Kritik und Weiterentwicklungen
Das grundlegende Solow-Modell geht von einer geschlossenen Volkswirtschaft ohne Staatstätigkeit aus. Eine Miteinbeziehung des Staatssektors und internationaler Kapitalflüsse ist allerdings möglich.[36]
Eine zentrale Annahme des Solow-Modells ist jedoch die exogen vorgegebene, über die Zeit konstante Sparquote. Diese bedeutet, dass eine Volkswirtschaft unabhängig vom Niveau ihres Einkommens immer den gleichen Prozentsatz desselben spart. Das Sparverhalten wird also nicht modelliert, und deswegen kann auch nicht untersucht werden, wie die Volkswirtschaft auf Änderungen des Zinssatzes oder des Kapitalsteuersatzes reagiert. Darüber hinaus deuten empirische Untersuchungen auch darauf hin, dass die Sparquote mit steigendem Einkommen steigt. Eine wichtige Erweiterung des Solow-Modells ist es deswegen, die Sparquote in Abhängigkeit vom Einkommen zu formulieren, was eine explizite Modellierung des Sparverhaltens der Haushalte erfordert. Eine solche wurde bereits von Ramsey 1928 eingeführt und dann von Cass (1965) und Koopmans (1965) weiterentwickelt.[37] Das resultierende Modell wird deswegen oft als Ramsey-Cass-Koopmans‑Modell oder kurz Ramsey-Modell bezeichnet.
Das Solow-Modell erklärt nicht weiter, was unter „Technologie“ oder „Arbeitsproduktivität“ zu verstehen ist. Es handelt sich dabei um einen Sammelbegriff für alle Faktoren, die das Pro-Kopf-Einkommen beeinflussen und nicht schon in Kapital und Arbeit inbegriffen sind. Dazu könnten unter anderem die Ausbildung der arbeitenden Bevölkerung, die Infrastruktur, aber auch politische Institutionen wie Eigentumsrechte gehören. Darüber hinaus nimmt das Modell diese für das Modell zentrale Wachstumsdeterminante als exogen gegeben an.[38] Während das Ramsey-Cass-Koopmans-Modell die Endogenisierung der Sparquote schaffte (d. h., die Sparquote wird aus dem Modell heraus erklärt und nicht als gegeben angenommen), behielt es die Annahme exogenen technologischen Fortschritts bei. Die Kritik an dieser Annahme führte Ende der 1980er Jahre zur Entwicklung sogenannter endogener Wachstumsmodelle, zu denen unter anderem Paul Romer, Philippe Aghion und Peter Howitt sowie Gene M. Grossman und Elhanan Helpman wichtige Beiträge verfassten (siehe auch Romer-Modell oder Jones-Modell). In diesen Modellen wird der technologische Fortschritt nicht als von außen vorgegebene Größe betrachtet, sondern bestimmt sich endogen innerhalb des Modells.[39]
Wachstumskritiker wie Herman Daly oder Nicholas Georgescu-Roegen kritisieren, dass im Solow-Modell die Rolle natürlicher Ressourcen nicht berücksichtigt würde.[40][41][42][43] Es existieren allerdings inzwischen Erweiterungen wie das „green Solow model“.[44][45]
Siehe auch
Weblinks
Literatur
- Robert Merton Solow: A Contribution to the Theory of Economic Growth. In: Quarterly Journal of Economics. Band 70, 1956, S. 65–94 (doi:10.2307/1884513).
- → Deutsche Übersetzung: H. König (Hrsg.): Ein Beitrag zur Theorie des wirtschaftlichen Wachstums. In: Wachstum und Entwicklung der Wirtschaft. Verlag Kiepenheuer & Witsch, Köln 1968, S. 67–96.
- Trevor Swan: Economic Growth and Capital Accumulation. In: Economic Record. Band 32, Ausgabe 2, 1956, S. 334–361 (doi:10.1111/j.1475-4932.1956.tb00434.x).
- Robert J. Barro, Xavier Sala-i-Martin: Economic Growth. 2. Auflage, MIT Press, Cambridge, MA 2004.
- → Deutsche Übersetzung der ersten Auflage (übersetzt von Walter Buhr): Wirtschaftswachstum. Oldenbourg Verlag, München 1998, ISBN 978-3-486-23535-7.
- Lucas Bretschger: Wachstumstheorie. 3. überarbeitete und erweiterte Auflage, Oldenbourg Verlag, München 2004, ISBN 3-486-20003-8, Kapitel 3, Seite 25–40.
- Manfred Gärtner: Macroeconomics. 2. Auflage, Pearson Education, Harlow 2006.
- David Romer: Advanced Macroeconomics. 3. Auflage, McGraw-Hill/Irwin, New York 2006.
- Daron Acemoglu: Introduction to Modern Economic Growth. Princeton University Press, 2008.
- Charles I. Jones: The Facts of Economic Growth. Stanford GSB and NBER, 2015.
- M. Burda; C. Wyplosz: Macroeconomics. A European Text. 4. Auflage, New York, 2005.
- Verena Halsmayer: From Exploratory Modeling to Technical Expertise: Solow's Growth Model as a Multipurpose Design. In: E. Roy Weintraub (Hrsg.): MIT and the Transformation of American Economics (= History of Political Economy. Volume 46, Supplement 1). 2014, S. 229–251, doi:10.1215/00182702-2716181 (englisch, academia.edu [abgerufen am 29. November 2017]).
Anmerkungen
- Siehe hierzu auch: Robert W. Dimand, Barbara J. Spencer: Trevor Swan and the Neoclassical Growth Model. NBER Working Paper 13950, April 2008.
- Daron Acemoglu: Introduction to Modern Economic Growth. Princeton University Press, Princeton 2009, S. 37.
- Barro, Sala-i-Martin: Economic Growth. S. 71–74.
- Für die Variablen gilt im Folgenden:
- Denkbar wäre auch eine allgemeinere Produktionsfunktion der Form . Tatsächlich ist aber nur technologischer Fortschritt, der den Produktionsfaktor Arbeit erhöht (sogenannter labour augmenting oder Harrod-neutraler Fortschritt), mit der Existenz eines langfristigen Gleichgewichts mit kontinuierlichem technologischen Fortschritt mit konstanter Rate vereinbar. Siehe Barro, Sala-i-Martin: Economic Growth. S. 52 f. und 78 ff.
- Nach Ken-Ichi Inada, der sie in seinem 1963 erschienenen Artikel On a Two-Sector Model of Economic Growth: Comments and Generalization (Review of Economic Studies 30.2, S. 119–127) formulierte.
- Barro, Sala-i-Martin: Economic Growth. S. 23–28.
- Barro, Sala-i-Martin: Economic Growth. S. 28.
- Gärtner: Macroeconomics. S. 246.
- Die Pro-Kopf-Fundamentalgleichung des Solow-Modells lässt sich wie folgt durch die Ableitung des Kapitalstocks nach der Zeit und Anwendung der Kettenregel angeben: , wobei und beachtet werden muss.
- Gärtner: Macroeconomics. S. 246 f.
- Daron Acemoglu: Introduction to Modern Economic Growth. Princeton University Press, Princeton 2009, S. 29, 33 und 39.
- Gärtner: Macroeconomics. S. 238 f., S. 246 f.
- Barro, Sala-i-Martin: Economic Growth. S. 38 f.
- Barro, Sala-i-Martin: Economic Growth. S. 44.
- bezeichnet die Ableitung der Variablen nach der Zeit : , somit gibt die Veränderung der Variablen zum Zeitpunkt an.
- Im Folgenden werden die Zeitindizes aus Vereinfachungsgründen weggelassen.
- Gärtner: Macroeconomics. S. 247.
- bezeichnet das Argument des Maximums.
- Barro, Sala-i-Martin: Economic Growth. S. 34 f.
- Barro, Sala-i-Martin: Economic Growth. S. 36 f.
- Barro, Sala-i-Martin: Economic Growth. S. 43.
- Gärtner: Macroeconomics. S. 248 f.
- Herleitung der Fundamentalgleichung: . Es gilt , und , sind definiert als und . Dadurch vereinfacht sich der Ausdruck zu .
- Gärtner: Macroeconomics. S. 248 f.
- Bretschger: Wachstumstheorie. S. 40.
- Moses Abramovitz: Resource and Output Trends in the United States since 1870. American Economic Review 46 (Mai 1956), S. 5–23.
- Robert M. Solow: Technical Change and the Aggregate Production Function. Review of Economics and Statistics, 39.3 (1957), S. 312–320.
- Romer: Advanced Macroeconomics. S. 29.
- Romer: Advanced Macroeconomics. S. 29.
- Dabei sind die Wachstumsraten der einzelnen Variablen wie folgt definiert:
- Romer: Advanced Macroeconomics. S. 29 f.
- Barro, Sala-i-Martin: Economic Growth. S. 45 ff.
- N. Gregory Mankiw, David Romer, David Weil: A Contribution to the Empirics of Economic Growth. In: Quarterly Journal of Economics. Band 107, Nr. 2, 1992, S. 407–437.
- Romer: Advanced Macroeconomics. S. 26 ff.
- Siehe Gärtner: Macroeconomics. Kapitel 10.1 und 10.2.
- Barro, Sala-i-Martin: Economic Growth. S. 85. Die zugrundeliegenden Arbeiten sind:
Frank P. Ramsey: A Mathematical Theory of Saving. Economic Journal 38 (152), S. 543–559.
David Cass: Optimum Growth in an Aggregative Model of Capital Accumulation. Review of Economic Studies, 32.3, S. 233–240.
Tjalling C. Koopmans: On the concept of optimal economic growth. In: (Study Week on the) Econometric Approach to Development Planning. Kapitel 4, S. 225–87, North-Holland Publishing Co., Amsterdam. - Romer: Advanced Macroeconomics. S. 28.
- Barro, Sala-i-Martin: Economic Growth. S. 19 f.
- Herman Daly: Georgescu-Roegen versus Solow/Stiglitz. In: Ecological Economics 1997; 22(3), S. 261–266.
- Herman Daly: Reply to Solow/Stiglitz. In: Ecological Economics 1997; 22(3), S. 271–273.
- Joseph E. Stiglitz: Georgescu-Roegen versus Solow/Stiglitz. In: Ecological Economics 1997; 22(3), S. 269–270.
- Robert M. Solow: Georgescu-Roegen versus Solow-Stiglitz. In: Ecological Economics 1997; 22(3), S. 267–268.
- William A. Brock, M. Scott Taylor: The green Solow model. In: Journal of Economic Growth 15.2, 2010, S. 127–153, doi:10.1007/s10887-010-9051-0.
- Steffen Lange: Macroeconomics Without Growth: Sustainable Economies in Neoclassical, Keynesian and Marxian Theories. Metropolis, Marburg 2018. ISBN 978-3-7316-1298-8. Kapitel 8.