Technische Fortschrittsfunktion

Die technische Fortschrittsfunktion wurde von dem Wirtschaftswissenschaftler Nicholas Kaldor entwickelt. Der technische Fortschritt wird an der Zuwachsrate der Arbeitsproduktivität gemessen. Diese Zuwachsrate wird als Funktion der Zuwachsrate der Kapitalintensität bestimmt. Damit ist der technische Fortschritt nicht mehr exogen gegeben, wie in den keynesianischen oder neoklassischen Wachstumsmodellen bis in die 70er Jahre, sondern bestimmt sich endogen in Abhängigkeit von der Veränderungsrate der Kapitalintensität. Insofern handelt es sich bei der technischen Fortschrittsfunktion um einen Vorläufer der späteren endogenen Wachstumstheorien.

Das Modell lässt sich als ein Fall von Ein-Gut-Parabel beschreiben, als von einem produzierten Gut ausgegangen wird, das entweder in einer bestimmten Menge je Arbeitsplatz eingesetzt (Kapitalintensität) oder für die Ausrüstung zusätzlicher Arbeitsplätze oder eben als Konsum verbraucht wird. Qualitative Veränderungen, sei es, dass neue und andere Arten von Produktionsmitteln eingesetzt werden oder dass neue und andere Konsumgüter hergestellt werden, müssen durch eine Mengenerhöhung des einen Gutes dargestellt werden, indem eben mehr Produkte je Arbeiter hergestellt werden, mehr Güter je Arbeiter eingesetzt (Kapitalintensität) oder konsumiert werden.

So lassen sich gewisse einfache Zusammenhänge darstellen. Aus Sicht des einzelnen Unternehmens ist nicht jede Erhöhung der Arbeitsproduktivität profitabel, sie muss ja mit einer Erhöhung der Kapitalintensität erkauft werden. Vereinfachend (unter Vernachlässigung der Lohnkosten) kann festgestellt werden, dass eine Erhöhung der Kapitalintensität um einen bestimmten Prozentsatz dann profitabel ist, wenn sie zu einer Erhöhung der Arbeitsproduktivität um einen höheren Prozentsatz, also zu einer über-proportionalen Erhöhung führt. Sind beide Prozentsätze gleich groß, dann rentiert die Einführung technischen Fortschritts nicht oder gerade noch, wie man es nehmen will. Die Annahme, dass die Arbeitsproduktivität und die Kapitalintensität mit gleicher Rate wachsen, ist eine übliche Gleichgewichtsannahme von Wachstumsmodellen.

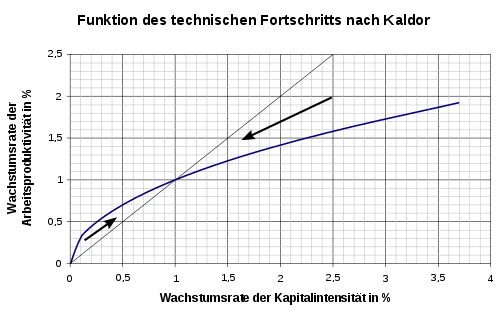
Die technische Fortschrittsfunktion

Kaldor machte über die Form der technischen Fortschrittsfunktion bestimmte Annahmen (siehe Abbildung[1]). Niedrige Wachstumsraten der Kapitalintensität führen überproportional zu höheren Wachstumsraten der Arbeitsproduktivität, höhere Wachstumsraten der Kapitalintensität aber nur noch zu unterproportional höheren Wachstumsraten der Arbeitsproduktivität. Dazwischen muss also eine Wachstumsrate der Kapitalproduktivität liegen (in der Abbildung 1 % Wachstum), die zu einer genau gleich hohen Wachstumsrate der Arbeitsproduktivität führt.

Stabilität

Dieser Punkt ist stabil nach Kaldor[2], denn solange die Wachstumsrate der Kapitalproduktivität zu einer noch höheren Wachstumsrate bei der Arbeitsproduktivität führt, werden die Unternehmen in der nächsten Periode versuchen, die Kapitalintensität noch stärker zu steigern. Führt eine Wachstumsrate der Kapitalintensität nur zu einer unterproportionalen Wachstumsrate der Arbeitsproduktivität, ist diese nicht rentabel und die Unternehmen werden in der nächsten Periode die Kapitalintensität nicht mehr so stark ausdehnen.

Hat also die technische Fortschrittsfunktion den von Kaldor behaupteten Verlauf, dann ergibt sich als Gleichgewichtszustand, dass Kapitalintensität und Arbeitsproduktivität mit gleicher Wachstumsrate wachsen, wie dies etwa auch im Harrod-Domar-Modell oder im Solow-Modell der Fall ist. Da diese technische Fortschrittsfunktion ein Gleichgewicht beinhaltet, wird sie als "well-behaved" bezeichnet, sie verhält sich wohl.

Nach Allen müsste jedoch der Anpassungsprozess mathematisch in einem Ungleichgewichtsmodell dargestellt werden, um entscheiden zu können, ober der Gleichgewichtspunkt tatsächlich stabil ist. Dies wäre jedoch keine einfache Aufgabe.[2]

Würden beliebig große Steigerungsraten der Kapitalintensität zu noch größeren Steigerungsraten der Arbeitsproduktivität führen, bestünde ein Anreiz für die Unternehmen, dauerhaft den gesamten Unternehmensgewinn nicht in zusätzliche Arbeitsplätze, sondern in die Ausdehnung des Kapitalstocks je Arbeitsplatz zu investieren. Wenn aber solch intensives Wachstum vorherrscht, es wird je Arbeitsplatz immer mehr investiert, nicht in neue Arbeitsplätze (extensives Wachstum), dann kommt es zu Widersprüchen auf gesamtwirtschaftlicher Ebene, was den Hintergrund auf physischer oder stofflicher Ebene zum Gesetz des tendenziellen Falls der Profitrate von Karl Marx bildet.

Mathematische Eigenschaften

Die technische Fortschrittsfunktion ist im Allgemeinen nicht integrierbar, das heißt, es lässt sich keine zu ihr „passende“ Produktionsfunktion angeben. Eine Ausnahme ist die Cobb-Douglas-Produktionsfunktion mit Harrod-neutralem, also arbeitssparendem oder arbeitsvermehrendem technischen Fortschritt mit konstanten Skalenerträgen.

Y: Produktionsmenge
K: Einsatz von Kapital
A: Einsatz von Arbeit
c: Konstante
t: Zeit
a: Parameter zwischen null und eins.
m: Rate des technischen Fortschritts

Die Cobb-Douglas-Produktionsfunktion mit arbeitssparendem technischen Fortschritt, der mit der Rate m wächst:

Y=c\cdot K^{a}\cdot (e^{m\cdot t}\cdot A)^{1-a}.

Mit A durchdividiert ergibt die Formulierung in Pro-Kopf-Variablen. Die Arbeitsproduktivität ist eine Funktion der Kapitalintensität:

{Y \over A}=c\cdot ({K \over A})^{a}\cdot e^{m\cdot t\cdot (1-a)}.

Wenn also Y/A=y (Arbeitsproduktivität) und K/A=k (Kapitalintensität)

y=c\cdot k^{a}\cdot e^{m\cdot t\cdot (1-a)}.

Der Übergang zu einer Funktion, die in den Wachstumsraten von Arbeitsproduktivität und Kapitalintensität formuliert ist, erfolgt durch die Ableitung des Logarithmus der Funktion $y(t)$ nach der Zeit $t$ :

\ln y=\ln c+a\cdot \ln k+m\cdot t\cdot (1-a),

nach der Zeit $t$ abgeleitet:

{\frac {1}{y}}\centerdot {\dot {y}}=a\cdot {\frac {1}{k}}\centerdot {\dot {k}}+m\cdot (1-a).

Links steht als abhängige Variable die Wachstumsrate der Arbeitsproduktivität, rechts des Gleichheitszeichens erscheint als erklärende Variable die Wachstumsrate der Kapitalintensität. Dabei sind

{\dot {y}}

und

{\dot {k}}

die Ableitungen nach der Zeit, außerdem sind die Wachstumsraten definiert als:

{{\dot {y}} \over y}={\hat {y}}

und

{{\dot {k}} \over k}={\hat {k}}

Es ergibt sich also die Wachstumsrate der Arbeitsproduktivität als eine lineare Funktion der Wachstumsrate der Kapitalintensität mit dem Achsenabschnitt $m(1-a)$ und der Steigung $a$ mit

{\hat {y}}=a\cdot {\hat {k}}+m\cdot (1-a).

Da $a$ unter der Annahme von konstanten Skalenerträgen der Cobb-Douglas-Funktion einen Wert zwischen null und eins annimmt, schneidet diese Kurve die 45°-Linie, so dass es einen Gleichgewichtswert gibt, in dem gilt, dass die Wachstumsrate der Arbeitsproduktivität gleich der Wachstumsrate der Kapitalintensität ist und beide gleich der Rate des technischen Fortschritts $m$ sind:

{\hat {y}}={\hat {k}}=m.

Einzelnachweise

Allgemeine Darstellung nach Allen 1968. Kaldor selbst ging von einer linearen Funktion mit positivem y-Achsen-Abschnitt aus und Steigung kleiner 1.
Allen S. 310

Literatur

Allen, R.G.D.: Macro-Economic Theory: A Mathematical Treatment. - London, Melbourne, Toronto: Macmillan, 1968.
Bergheim, Stefan: "Pair-wise cointegration in long-run growth models". Deutsche Bank Research. Working Papers Series. Research Notes 24. February 9, 2007. (Es wird eine technische Fortschrittsfunktion à la Kaldor ökonometrisch geschätzt.)
Kaldor, Nicholas (1957): "A Model of Economic Growth." The Economic Journal. pp. 591–624.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Allgemeine Darstellung nach Allen 1968. Kaldor selbst ging von einer linearen Funktion mit positivem y-Achsen-Abschnitt aus und Steigung kleiner 1.

[Alle-2] Allen S. 310