Produktionsfunktion
Eine Produktionsfunktion beschreibt in der Produktionstheorie die Beziehung zwischen den Inputs und den sich daraus ergebenden Outputs. Somit gibt eine Produktionsfunktion die höchste Produktionsmenge an, die ein Unternehmen mit Hilfe der Kombination von Inputs produzieren kann.
Arten der Produktionsfunktion
Eine Produktionsfunktion wird durch das verwendete Produktionsverfahren für ein Gut bestimmt. Dabei unterscheidet man folgende Arten:
Substitutional
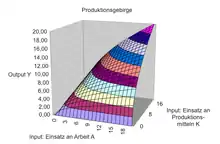
Bei einer substitutionalen Produktionsfunktion kann ein Produktionsfaktor (zumindest innerhalb bestimmter Grenzen) durch einen anderen oder die Kombination von anderen Produktionsfaktoren ersetzt (substituiert) werden. Ein weiteres Kennzeichen der Substitutionalität ist, dass die Outputmenge durch veränderte Einsatzmengen nur eines Faktors bei Konstanz der übrigen Faktormengen beeinflusst werden kann. Hinsichtlich der Substitutionalität kann man zwischen der totalen und der peripheren Substitutionalität unterscheiden. Totale Substitutionalität liegt vor, wenn ein Faktor vollständig durch einen anderen ersetzt werden kann. Dabei kann die Einsatzmenge des Faktors auch null betragen. Analytisch berechenbar durch Auflösen der Produktionsfaktoren und durch die Ableitung der Isoquantengleichung. Periphere Substitutionalität ist dadurch gekennzeichnet, dass der Austausch der Produktionsfaktoren nur innerhalb bestimmter Grenzen möglich ist.
Eine Untergruppe bilden die sogenannten CES-Produktionsfunktionen, die sich durch eine konstante Substitutionselastizität auszeichnen. Das bekannteste und in der VWL am häufigsten verwendete Beispiel einer substitutionalen Produktionsfunktion ist die Cobb-Douglas-Produktionsfunktion.
Ertragsgesetzlich
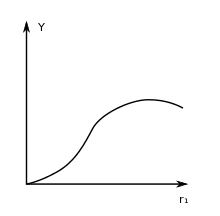
Hierbei handelt es sich um die wohl älteste Produktionsfunktion. Sie beruht auf Beobachtungen in der Landwirtschaft und wurde von Turgot als Gesetz vom abnehmenden Bodenertrag formuliert. Es wird von zwei Faktoreinsatzmengen und einer Ausbringungsmenge ausgegangen. Seine Beobachtungen zeigten, dass durch die Erhöhung von Arbeitseinsatz oder Dünger das Produktionsergebnis zunächst steigt, aber ab einer bestimmten Faktoreinsatzmenge die Ausbringungsmenge stetig fällt.
Cobb-Douglas
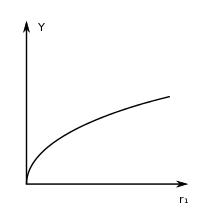
Die Cobb-Douglas-Produktionsfunktion wurde im Jahre 1928 von Charles Wiggins Cobb und Paul Howard Douglas entwickelt. Im Vergleich zur ertragsgesetzlichen Produktionsfunktion gibt es bei dieser Produktionsfunktion kein Maximum, d. h., es wird davon ausgegangen, dass die Erhöhung des Faktoreinsatzes immer eine höhere Ausbringungsmenge zur Folge hat. Der durch zunehmenden Faktoreinsatz erzielte Ertrag nimmt jedoch ab, d. h., wenn man z. B. die Einsatzmenge verdoppelt, so steigt der Ertrag zwar an, jedoch auf weniger als das Doppelte.
Limitational
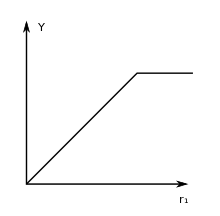
Hierbei stehen die Faktoren in einem bestimmten Einsatzverhältnis, d. h., der Ertrag steigt nur dann, wenn beide Faktoren vermehrt eingesetzt werden. Dies gilt jedoch nur, wenn beide Faktoren im gleichen Maße vorhanden sind, d. h., wenn ein Faktor im Überschuss da ist, so gilt dies nicht. In diesem Falle reicht die Erhöhung des anderen Faktors, um die Ausbringungsmenge zu erhöhen. Dies gilt so lange, bis der Überschussfaktor verbraucht ist. Um eine weitere Steigerung der Ausbringungsmenge zu erreichen, müssen also wieder beide Faktoren erhöht werden. Bis zu diesem Zeitpunkt erhöht sich der Ertrag nicht. Dies ist in dem Knick der Ertragsfunktion zu erkennen. Effizient ist diese Produktion jedoch nur, wenn kein Faktor verschwendet wird, d. h., wenn das richtige Einsatzverhältnis eingehalten wird.
Linear-limitational
Die Produktionsfaktoren stehen in einem festen Verhältnis zueinander und in einem festen Verhältnis zum Ausstoß (Output) eines Betriebes oder einer Anlage. Eine bekannte Vertreterin dieses Typs ist die Leontief-Produktionsfunktion.
Nichtlinear-limitational
Ein Vertreter nichtlinear-limitationaler Produktionsfunktionen ist die Gutenberg-Produktionsfunktion.
Weitere Typen und neuere Ansätze
| Produktionstyp | Name | Inhalt |
|---|---|---|
| B | Gutenberg-Produktionsfunktion | Input- und Outputmengen werden mithilfe der Intensität der verarbeitenden Betriebsmittel in Beziehung gesetzt; für eine gegebene Leistungsintensität des Betriebsmittels gelten dann limitationale Produktionszusammenhänge zwischen Input und Output |
| C | Heinen-Produktionsfunktion | Produktionsprozesse werden in Elementarvorgänge zerlegt, die Beziehungen zwischen technischen und ökonomischen Leistungen lassen sich eindeutig aufstellen |
| D | Pichler-Produktionsfunktion | Durchsatzfunktionen aufgestellt für limitationale und substitutionale Modelle |
| E | Kloock-Produktionsfunktion | Betrieb wird in Teilbereiche zerlegt, mehrstufige Produktionsprozesse mit zyklischen Verflechtungen aufgezeigt und Input-Output-Matrizen aufgestellt |
| F | Küpper-Produktionsfunktion | Input-Output-Matrizen werden dynamisiert, durch Berücksichtigung der Dauer des Produktionsprozesses |
| G | Matthes-Produktionsfunktion | Dynamisches Produktionsmodell wird mithilfe eines Netzplanes entwickelt, dieses wird dann mit der Produktionsfunktion von Heinen und den Anpassungsformen kombiniert |
Die Theorie der Produktionsfunktionen wurde insbesondere durch Einbeziehung der Umwelt als natürlichem Produktionsfaktor weiterentwickelt.
Als nachteilig hat sich die unscharfe Trennung zwischen den Größen In- und Output (oder auch Einsatz und Ausbringung) und der eigentlichen Transformation erwiesen. Neuere Ansätze der Produktionstheorie trennen die Bestandsgrößen In- und Output von den Transformationgrößen Verbrauch und Erzeugung. Schließlich bedeutet die Hereinnahme von Faktoren in den Betrieb nicht zwangsläufig auch deren Verbrauch in der Produktion (z. B. durch Schwund). Umgekehrt muss ein erzeugtes Gut nicht als Output den Betrieb verlassen (z. B. durch Ausschuss).
Die Transformation lässt sich gut durch die ingenieurwissenschaftlichen Funktionen des technischen Verbrauchs und der technischen Erzeugung beschreiben, wodurch die Integration der Ingenieurwissenschaften in die betriebswirtschaftliche Produktionsfunktion gelingt.
Im Gegensatz zu den volks- und betriebswirtschaftlichen Produktionsfunktionen steht in den ingenieurwissenschaftlichen Funktionen neben Verbrauch und Erzeugung insbesondere die technische Einstellung und technische Auslegung von Produktionssystemen im Vordergrund.
Eigenschaften von Produktionsfunktionen
- Additiv separabel
Literatur
- Dirk Diedrichs, Marco Ehmer und Nikolaus Rollwage: Mikroökonomie mit Kontrollfragen und Lösungen. WRW-Verlag, 2005. ISBN 3927250716
- Daniel Rubinfeld und Robert Pindyck: Mikroökonomie. Pearson Studium, 2003. ISBN 3827372828