Goldene Regel der Akkumulation

Die Goldene Regel der Akkumulation von Edmund S. Phelps besagt, dass im Solow-Modell der Konsum je Kopf der Bevölkerung oder je Arbeitnehmer dann maximiert wird, wenn der Zinssatz gleich der Wachstumsrate des Bruttoinlandsprodukts ist. Die Herleitung dieser Regel beruht auf einer Reihe von vereinfachenden Voraussetzungen. Die Regel ist auch weiterentwickelt worden, etwa indem Zeitpräferenzen der Konsumenten berücksichtigt werden (Ramsey-Regel).

Der mit Hilfe der Goldenen Regel gewonnene Zinssatz könnte dann als „gleichgewichtiger Realzinssatz“ in der Taylor-Regel zur Ermittlung des Taylor-Zinssatzes verwendet werden.

Annahmen

Zur Herleitung der Regel werden einige Annahmen gemacht:

Die Wachstumsrate der Bevölkerung/Beschäftigung L ist exogen gegeben. Das Arbeitsangebot L wächst wie die Bevölkerung mit einer „natürlichen Wachstumsrate“ n:
${\frac {{\dot {L}}(t)}{L(t)}}={\hat {L}}(t)=:n$ , wobei ${\dot {L}}(t)$ die Ableitung einer Variablen nach der Zeit darstellt ${\dot {L}}(t)={\frac {dL(t)}{dt}}$
Das Produkt Y teilt sich auf in Konsum C und in Investitionen I. Exporte und Importe werden also vereinfachend nicht berücksichtigt (geschlossene Volkswirtschaft).
Die Ersparnis S wird zur Finanzierung von Investitionen I in gleicher Höhe verwendet. („S gleich I“)
$Y(t)=C(t)+I(t)$ oder $Y(t)=C(t)+S(t)$
Es wird ein steady-state-Wachstum angenommen, also alle wirtschaftlichen Größen wachsen mit der gleichen Wachstumsrate, die dann – wenn kein technischer Fortschritt vorliegt – der natürlichen Wachstumsrate n des Arbeitskräfteangebots entsprechen muss.
Schließlich wird eine Produktionsfunktion angenommen, das heißt, die Produktion oder der Output Y (die Menge davon) hängt davon ab, wie viel der beiden Produktionsfaktoren Arbeitskräfte L und „Kapital“ (die Produktionsmittel) K eingesetzt werden. Darüber hinaus wird über die Form der Produktionsfunktion die vereinfachende Annahme gemacht, dass sie linear-homogen ist. Linear homogene Produktionsfunktionen haben die mathematische Eigenschaft, dass sie so umgeformt werden können, dass die Produktion je Arbeiter Y/L, als y bezeichnet, eine Funktion des Kapitaleinsatzes je Arbeiter K/L, als k bezeichnet, ist.

Unter all diesen Annahmen lässt sich eine mathematische Beziehung (Funktion) formulieren, nach welcher der Konsum je Arbeiter C/L bestimmt wird durch den Kapitaleinsatz je Arbeiter K/L (als k bezeichnet).

Dieses C/L soll maximiert werden, indem nach dem üblichen mathematischen Verfahren nach k abgeleitet und das Ergebnis gleich Null gesetzt wird (die erste Ableitung wird gleich Null gesetzt, um den Extrempunkt zu finden).

Im Einzelnen:

Steady-State-Wachstumsrate

Der Zuwachs des Kapitalstocks ${\dot {K}}$ ist gleich den Investitionen I, die wiederum durch die Ersparnisse S finanziert werden:

{\dot {K}}(t)=I(t)=S(t)

Sparquote: $s={\frac {S(t)}{Y(t)}}={\frac {{\dot {K}}(t)}{Y(t)}}$

Die Konsumfunktion: $C(t)=(1-s)Y(t)$ mit $s\in [0;1]$

Kapitalintensität: $k(t)={\frac {K(t)}{L(t)}}$

Pro-Kopf-Produktion: $y(t)={\frac {Y(t)}{L(t)}}$

Produktionsfunktion:

Y(t)=F(K(t),L(t))

Linear homogene Produktionsfunktion

F(\lambda K(t),\lambda L(t))=\lambda F(K(t),L(t))

\lambda ={\frac {1}{L}}:

{\frac {1}{L}}\cdot Y(t)=F\left({\frac {1}{L}}\cdot K(t),{\frac {1}{L}}\cdot L(t)\right)

also kann die Produktionsfunktion auch in Pro-Kopf-Größen ausgedrückt werden. Die Produktion je Arbeiter hängt ab von der Kapitalausstattung je Arbeiter (Kapitalintensität):

y(t)=F(k(t),1)=f[k(t)]

Die Wachstumsrate der Bevölkerung/Beschäftigung L ist exogen gegeben:

{\frac {{\dot {L}}(t)}{L(t)}}={\hat {L}}(t)=n

Steady-State-Wachstumsrate, alle Größen sollen mit der gleichen Rate wachsen:

{\frac {{\dot {Y}}(t)}{Y(t)}}={\frac {{\dot {L}}(t)}{L(t)}}={\frac {{\dot {K}}(t)}{K(t)}}=n

{\frac {{\dot {K}}(t)}{K(t)}}={\hat {K}}(t)=s\cdot {\frac {Y(t)}{K(t)}}=s{\frac {y(t)}{k(t)}}=n

s{\frac {y(t)}{k(t)}}=s{\frac {f(k(t))}{k(t)}}=n

sf(k(t))=nk(t)

Maximierung des Pro-Kopf-Konsums

Diese Graphik zeigt, wie der Kapitalstock

k^{\mathrm {gold} }

und die zugehörige Sparquote

s^{\mathrm {gold} }

den langfristigen Gleichgewichtskonsum

c^{*}

der Volkswirtschaft maximieren. Das Maximum liegt bei

c^{\mathrm {gold} }

.

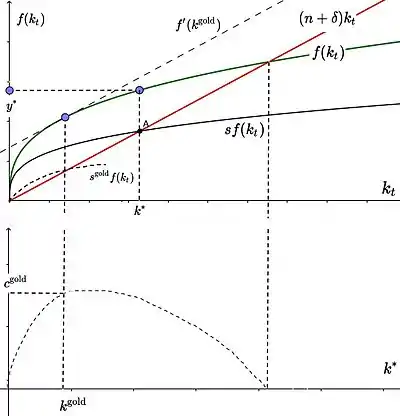
Bei welcher Steady-State-Wachstumsrate wird der Konsum je Kopf

{\frac {C(t)}{L(t)}}

maximiert?

{\frac {C(t)}{L(t)}}=(1-s){\frac {Y(t)}{L(t)}}=(1-s)y(t)=(1-s)f(k(t))

Laut Steady State gilt:

s\cdot f(k(t))=(n+\delta )\cdot k

Also:

{\frac {C(t)}{L(t)}}=f(k(t))-(n+\delta )\cdot k

Maximierung des Pro-Kopf-Konsums bezüglich k bedeutet nach k ableiten und gleich null setzen:

f^{\prime }(k(t))-(n+\delta )=0

Goldene Regel der Akkumulation

Die Grenz-Produktivität des Kapitals $f^{\prime }(k)$ muss also gleich der Wachstumsrate $(n+\delta )$ sein. Neoklassisch wird angenommen, dass die Grenzproduktivität des Kapitals gleich dem Preis für den Kapitaleinsatz ist, also gleich der Profitrate bzw. dem Zinssatz.

Nebenrechnung zur Grenzproduktivität des Kapitals

Grenzproduktivität des Kapitals als partielle Ableitung von F(K,L) nach K:

{\frac {\partial F(K,L)}{\partial K}}

Lineare Homogenität:

F(K,L)=L\cdot F\left({\frac {K}{L}},1\right)=L\cdot f(k)

Teilrechnung (mit Anwendung der Kettenregel):

{\frac {\partial F({\frac {K}{L}},1)}{\partial K}}={\frac {\partial F({\frac {K}{L}},1)}{\partial {\frac {K}{L}}}}\cdot {\frac {\partial {\frac {K}{L}}}{\partial K}}

=f^{\prime }(k){\frac {1}{L}}

Insgesamt also:

{\frac {\partial F(K,L)}{\partial K}}=f^{\prime }(k)

Empirische Überprüfung

Profitquote gleich Investitionsquote

Die Goldenen Regel der Akkumulation besagt also, dass im optimalen Falle der Zinssatz gleich der Steady-State-Wachstumsrate sein soll, insbesondere also:

i={\frac {{\dot {K}}(t)}{K(t)}}

Multipliziert man links und rechts mit K und dividiert man mit Y, dann erhält man:

{\frac {i\cdot K(t)}{Y(t)}}={\frac {{\dot {K}}(t)}{Y(t)}}

,

wobei

{\dot {K}}(t)=I(t)

ist.

Investitionen im Verhältnis zu den Gewinnen

Links der Gleichung steht damit die Profitquote (Gewinnquote, der Anteil der Gewinne am BIP) und rechts steht die Investitionsquote, der Anteil der Investitionen am BIP. Ob beides tatsächlich gleich ist, kann empirisch überprüft werden.

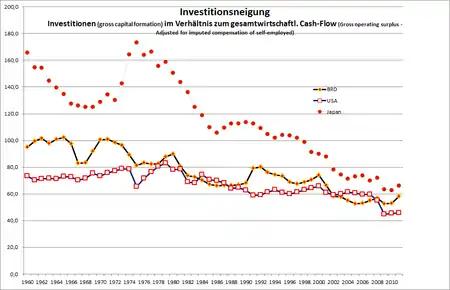
Ist die Investitionsquote (gleich der Sparquote, einschließlich der Abschreibungen) höher als die Profitquote (einschließlich der Abschreibungen, also gleich der Cash-Flow-Quote), dann liegt (laut Lutz Arnold S. 54) „dynamische Ineffizienz“ vor. Laut Arnold kommen Studien für die OECD-Länder zu dem Ergebnis, dass es eher umgekehrt war, eher war die Profitquote höher als die Investitionsquote.

Die Profitquote lag dabei bei rund einem Drittel, die Investitionsquote bei etwa 10 % bis 20 %. Die Profitquote ist dabei einschließlich der Steuern. Eine Studie des IWF kommt zu dem Ergebnis, dass die weltweite Spar- und Investitionsquote, gemessen am Bruttoinlandsprodukt, von etwa 24 % 1970 auf etwa 22 % 2004 abgenommen hat.

Während dieses Ergebnis also laut Arnold „dynamische Ineffizienz“ widerlegt, stellt sich andererseits die Frage, ob die Regel „Die Gewinne von heute sind die Investitionen von morgen (und die Arbeitsplätze von übermorgen)“, die sogenannte G-I-B-Formel, stimmt, wenn die Investitionsquote tatsächlich spürbar niedriger als die Profitquote ist, bzw. wie andere Untersuchungen zeigen, hinter der Profitquote immer weiter zurückbleibt (Sparschwemme). In der Abbildung sind die Bruttoanlageinvestitionen im Verhältnis zum gesamtwirtschaftlichen "Cash Flow", hier Gewinne vor Abzug der Steuern zuzüglich der Abschreibungen dargestellt. Die so definierte Investitionsneigung geht in den Ländern der Triade USA, Japan und BRD tendenziell zurück.

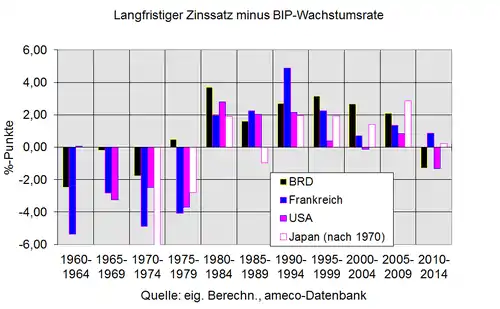
Zinssatz gleich Wachstumsrate

Die goldene Regel kann auch unmittelbar überprüft werden, indem man die Wachstumsrate des BIP mit dem Zinssatz vergleicht. In der Abbildung wird die Differenz gebildet zwischen BIP-Wachstumsrate und langfristigem Zinssatz. Demnach lagen die langfristigen Zinssätze bis zu den 1970er Jahren eher zu niedrig, seit den 1980er Jahren eher zu hoch. Seit den 1980er Jahren waren also die Einkommen des Produktionsfaktors Kapital gemessen an der goldenen Regel eher zu hoch.

Langfristiger Zinssatz minus BIP–Wachstumsrate

Literatur

Lutz Arnold: Wachstumstheorie. Vahlen Verlag, München 1997, ISBN 3-8006-2242-4

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.